

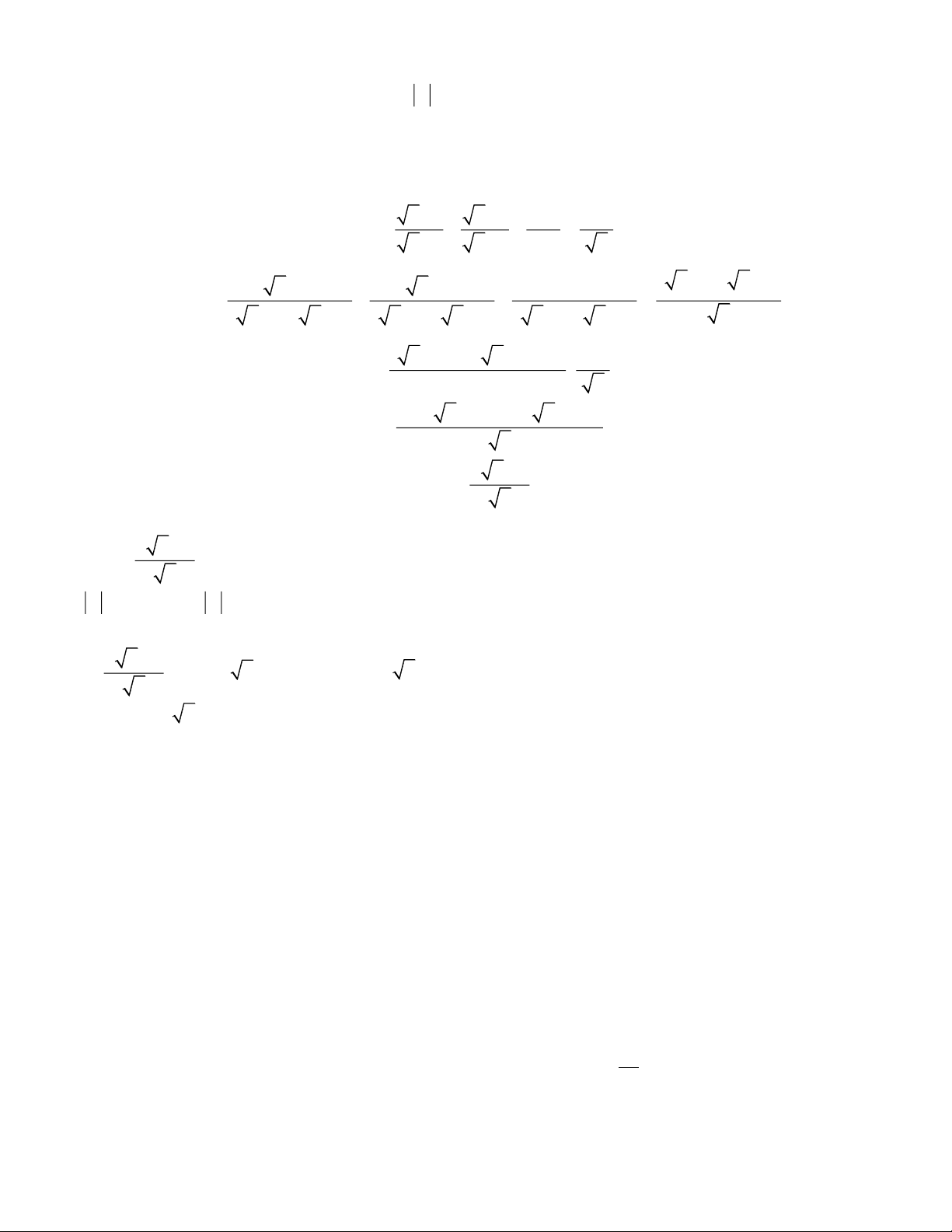

Preview text:
UBND TİNH HÀ NAM
KỲ THI TUYỂN SINH LÔP 10 THPT
SỎ GIÁO DỤC VÀ ĐÀO TAO NĂM HOC 2025-2026 ĐỀ CHÍNH THỨC
Môn: TOÁN (Đề chung)
(Dẻ này có 02 trang)
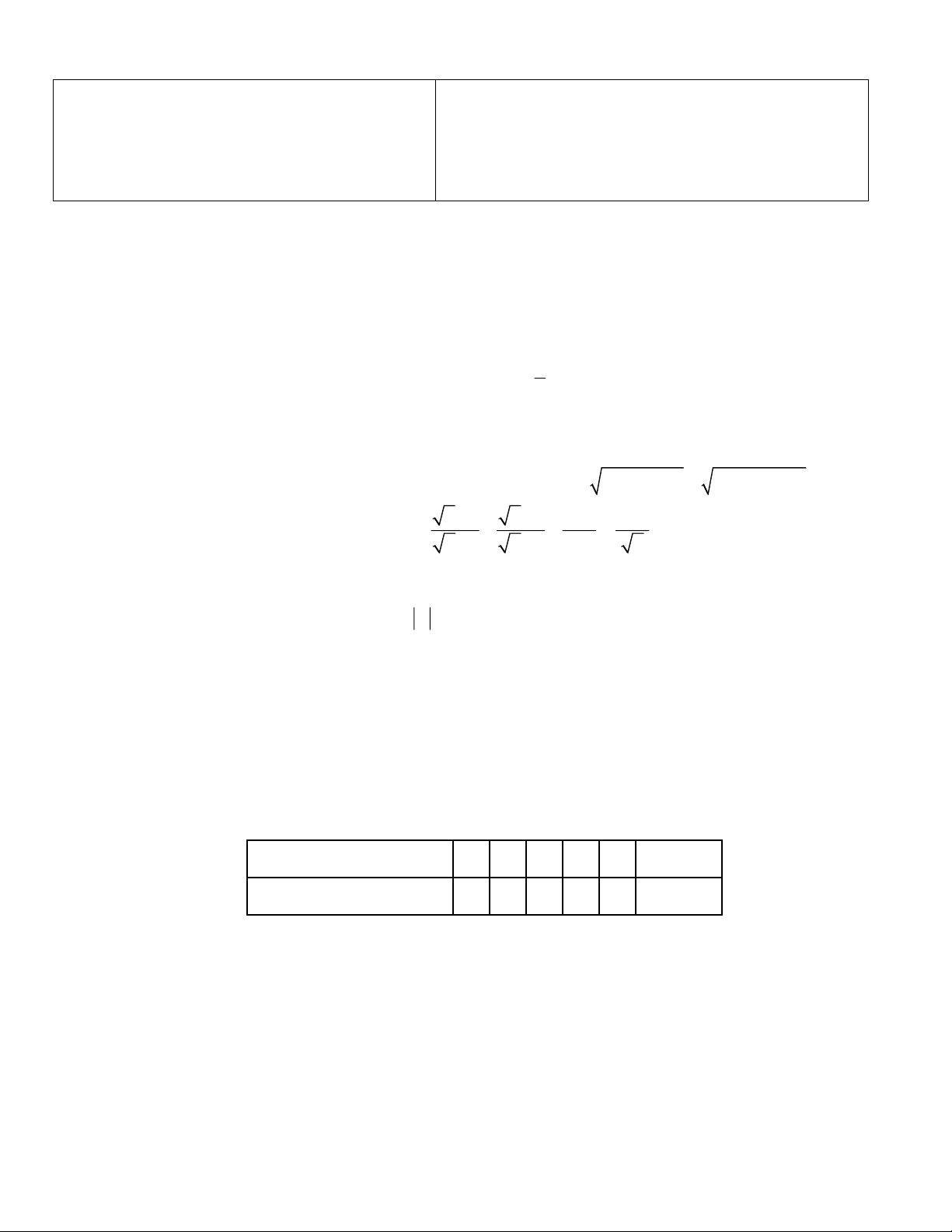
Thời gian làm bài: 120 phút, không kê thời gian giao đê ĐỀ Cāu 1. (2,5 điểm) 2x − y = 7 −
1. Giải hệ phương trình x + 2y = 4
2. Tìm tọạ độ tất cả các điểm thuộc đồ thị hàm số 1 2
y = x có tung độ bằng 4 4 3. Cho phương trình 2
x − 7x + 2 = 0
a , Chứng minh rằng phương trình đā cho có hai nghiệm phân biệt x , x 1 2
b , Không giải phương trình, tính giá trị của biếu thức 2 2
T = x + 2x +1 + 2x − x +11 1 1 2 2 + − −
Câu 2 ( 1,0 điểm) Cho biểu thức x 1 x 1 8 x 1 P = − −
, vời x 0 và x 1 x −1 x +1 x 1 − x
4. Rút gọn biểu thức P
5. Tìm tất cả các số nguyên x sao cho P + P = 0
Câu 3 ( 1,0 điểm). Một công ty vận tải Y dự dịnh sử dụng một đoàn xe để chở 80 tấn hàng hoá. Trước
khi khởi hành, do phát sinh công ty Y phải chở thêm 4 tấn hàng nữa, vì thế công ty đã điều thêm 2 xe
cùng tham gia vận chuyển nên tất cả các xe đều chở giảm đi 1 tấn hàng so với ban đầu. Hỏi ban đầu
công ty Y dự định sử dụng bao nhiêu xe, biết rằng tất cả các xe công ty sử dụng đều cùng chủng loại và chở cùng khối lượng? Câu 4 ( 1,5 diểm)
1. Điều tra thời gian tự học của 20 học sinh trong một ngày, thu được bảng tần số sau:
Thời gian tự học (giờ) 1 2 3 4 5 Cộng Tản sô (n) 5 4 6 3 2 N = 20
a , Lập bảng tần số tương đối của bảng tần số trên.
b , Tính tỉ lệ phần trăm số học sinh có thời gian tự học ít nhất 3 giờ trong một ngày.
2. Một hộp có 20 chiếc thẻ cùng loại, mỗi chiếc thẻ được ghi một trong các số 1, 2,3,, 20 ; hai thẻ khác
nhau được ghi hai số khác nhau. Rút ngẩu nhiên một chiếc thẻ trong hộp trên và quan sát số ghi trên thẻ
đó. Tỉnh xác suất của biến cố A : "Số ghi trên chiếc thẻ rút được chia hết cho cả 2 và 3 Trang 1
Câu 5 (3,0 điểm) Cho đường tròn (O; R) và điểm M nằm ngoài (O) . Từ điểm M kẻ hai tiếp tuyến M ,
A MB với (O)( ,
A B là hai tiếp điểm). Xét điểm D thuộc cung lờn AB ( D không nầm chính giữa
cung AB ), đường thẳng MD cắt (O) tại điểm C . Gọi E là trung điểm của dây CD , tia BE cất đường
tròn (O) tại điểm F .
1. Chứng minh bốn điểm M , ,
A O, B cùng thuộc một đường tròn.
2. Chứng minh hai tam giác EBC và EDF đồng dạng.
3. Chựng minh EM là tia phân giác của AEB
4. Khi D thay đổi trên cung lớn AB , tìm vị trí của D để diện tích tam giác MDF lớn nhất. Câu 6 ( 1,0 diểm)
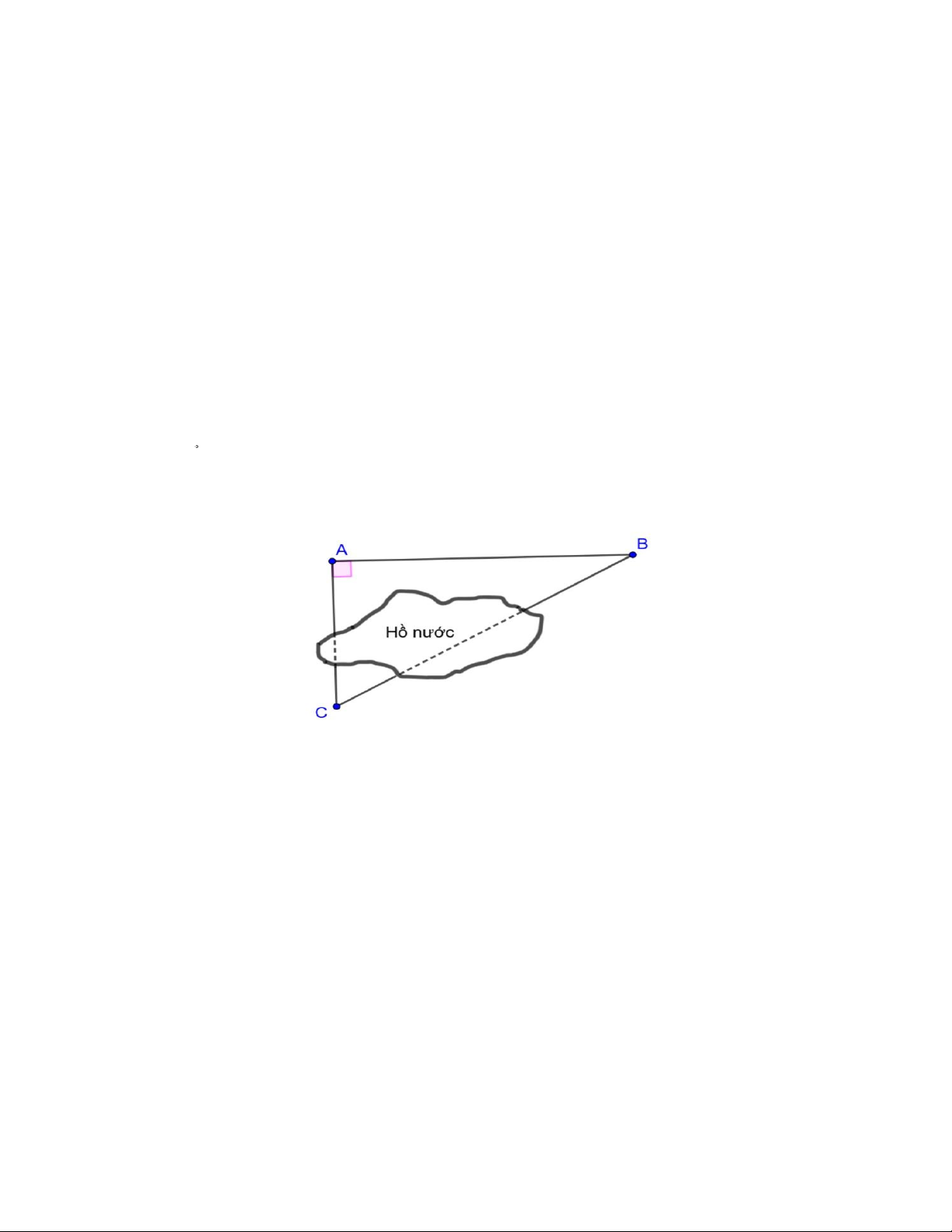
Hình 1 mô tả ba địa điểm nằm ở ba vị trí là ba đỉnh của tam giác ABC vuông tại A . Do điều kiện
thực tế không đo được trực tiếp khoảng cách từ B đến C , nhưng đo được AB = 200 m và
ABC = 30 . Tính khoảng cách BC (kết quả làm tròn đến hàng đơn vị của mét). Hinh 1
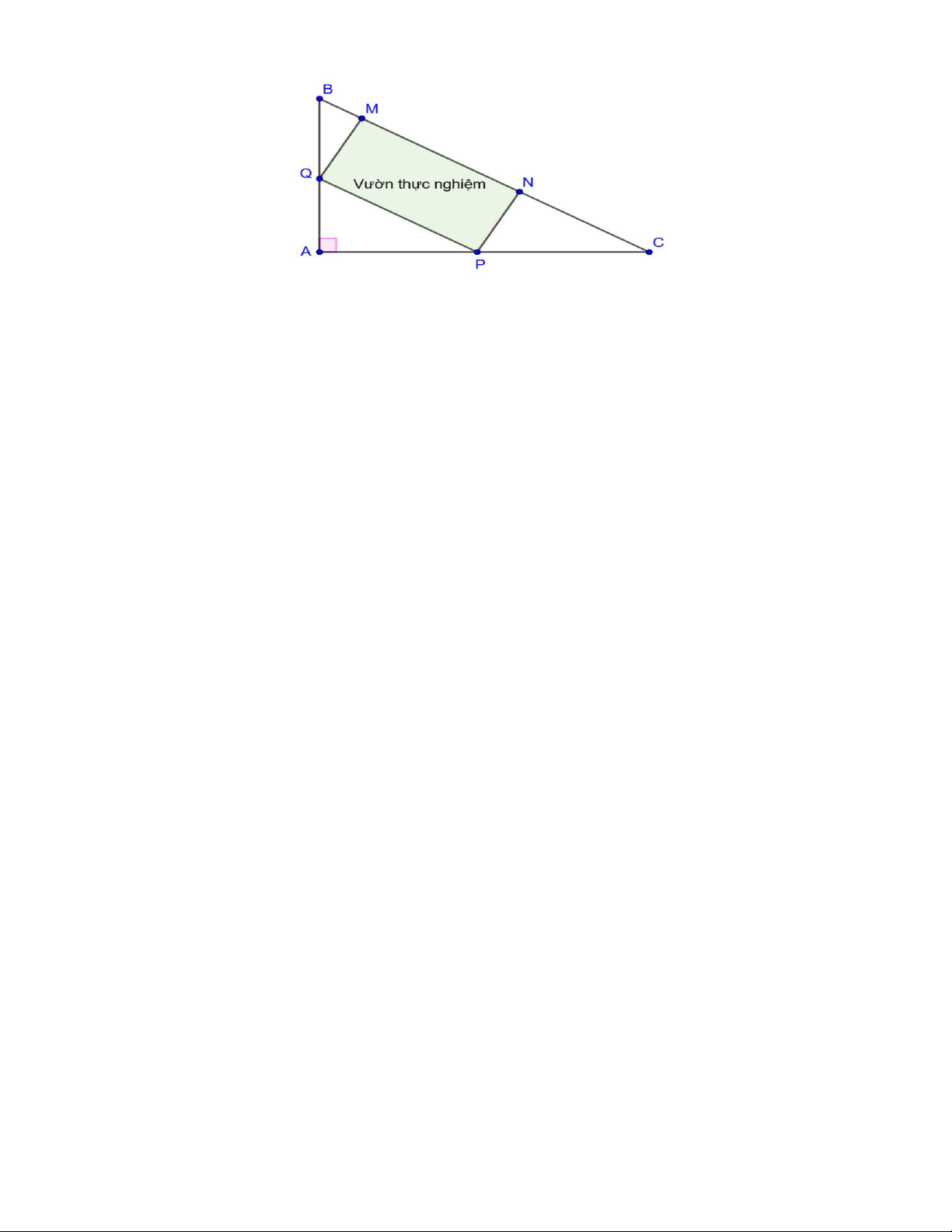
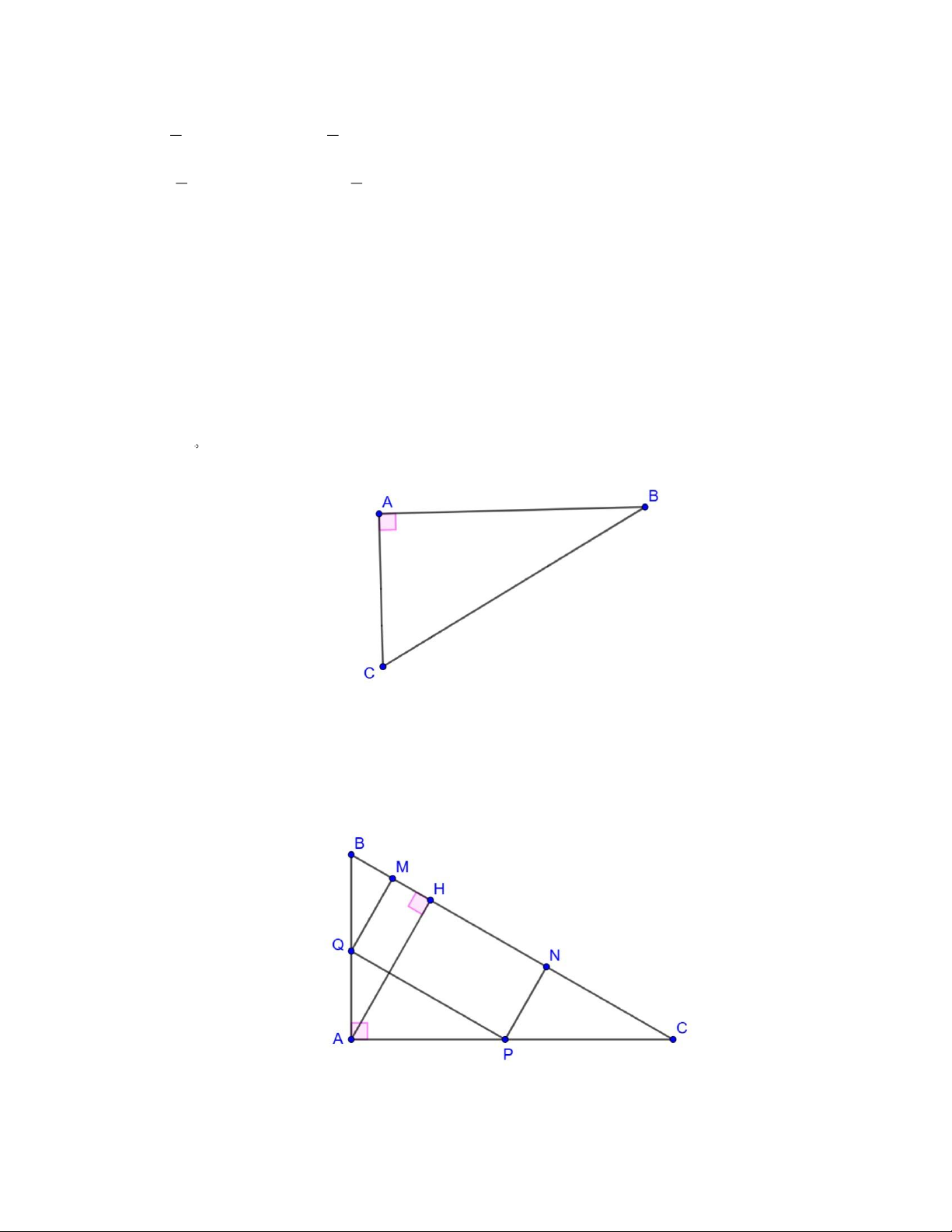
2. Trường THCS X đang khảo sát điểm làm một vườn thực nghiệm hình chữ nhạt MNPQ trên khu đất
dạng tam giác ABC vuông tại A nằm ở góc khuôn viên nhà trường (như hình 2), với
AB = 6 m, AC = 8 m . Biết rằng chi phí làm 2
1 m vườn thực nghiệm là 1,2 triệu đồng, hỏi nhà trường cần
chi bao nhiêu triệu đồng để diện tích khu vườn làm được là lớn nhât? Hình 2 Trang 2 Trang 3 2 Lời giải Bài toán 1 Câu 1. (2,5 điểm) 2x − y = 7 −
1. Giải hẹ̃ phương trình x + 2y = 4
2. Tìm tọa đọ tất cả các điểm thuộc đồ thị hàm số 1 2
y = x có tung đọ bầng 4 4 3. Cho phương trình 2
x − 7x + 2 = 0
a , Chứng minh ràng phương trình đã cho có hai nghiẹm phãn biệt x , x 1 2
b , Khōng giải phương trình, tính giá trị của biểu thức 2
T = x + 2x +1 + . 2 2x − x +11 1 1 2 2 Lời giải.
1. Hẹ̃ phương trình đã cho viết lại thành:
2x − y = −7 x + 2y = 4
2x − y = −7 2
( x + 2y) = 2.4
2x − y = −7 2x + 4y = 8 2x − y = −7 ( 2x + 4y
)−(2x − y) = 8−(−7)
2x − y = −7 5y = 15 2x − 3 = 7 − y = 3 x = −2 y = 3
Vạy hệ phương trìnla đã cho ớ ughiệm duy uhất ( x, y) = ( 2 − ,3)
2. Do điểm cần tìm có tung đọ bà̀ng 4 nēn thay y = 4 vào phương trình đồ thị hàm số, ta có Trang 4 1 2 4 = x 4 2 4.4 = x 2 x = 16 x = 4 x = −4
Vậy các điểm thoả mãn yēu càu là A(4;4) và B (−4;4)
3. a , Xét phương trình 2
x − 7x + 2 = 0(*) là phương trình bặc hai dạng 2
ax + bx + c = 0 với a = 1,b = 7, − c = 2 Phương trình () có 2 2
Δ = b − 4ac = ( 7 − ) − 4.1.2 = 41 0
Vặy nēn phương trình () có hai nghiẹ̃m phản biệt x , x (dpcm) 1 2 b − x + x = = 7 1 2
b , Theo định lý Viète, ta có a c x x = = 2 1 2 a
Nhận xét: Do x x = 2 0 nẽn x , x cùng dấu, mà x + x = 7 0 suy ra x , x dương. Do x là nghiệm 1 2 1 2 1 2 1 2 2 phương trình nēn 2
x − 7x + 2 = 0 , từ đó ta có 2 2 2
2x − x +11− ( 2 x + 6x + 9 = 0 2 2 2 2 ) 2 2
2x − x +11 = x + 6x + 9 2 2 2 2 Suy ra: 2 2
T = x + 2x +1 + 2x − x +11 1 1 2 2 2 2
T = x + 2x +1 + x + 6x + 9 1 1 2 2 T = ( x + )2 1 + ( x + 3)2 1 2
T = x +1 + x + 3 1 2
T = x +1+ x + 3 do x , x 0 1 2 ( 1 2 )
T = x + x + 4 1 2 T = 7 + 4 T = 11 Vạy T = 11 Bài toán 2 + − −
Câu 2 ( 1,0 điểm) Cho biểu thức x 1 x 1 8 x 1 P = − −
, với x 0 và x 1 x −1 x +1 x 1 − x
1. Rút gọn biểu thức P Trang 5
2. Tìm tât cả các số nguyēn x sao cho P + P = 0 Lời giải.
1. Với x 0, x 1 ta có x +1 x −1 8 x −1 P = − − x −1 x +1 x 1 − x 2 2
( x − )1( x x x + + − )1 ( 1) ( 1) 8 P ( = − − x
)1( x )1 ( x )1( x )1 ( x )1( x )1 − + − + − + x 2 2
( x +1) − ( x −1) − 8 x −1 P = x −1 x
x + 2 x +1− x + 2 x −1− 8 P = x 4 x − 8 P = x − Vặy 4 x 8 P =
với x 0, x 1 x
2. P + P = 0 nēn P = −P
khi và chỉ khi P„ 0 −
Hay 4 x 8„ 0 mà x 0, x
0 nēn 4 x −8„ 0 x
Từ đó suy ra x„ 2 hay x„ 4 0 x„ 4
Kết hợp với điều kiện xác định x 0, x 1 nēn
mà x nguyēn nēn x 2;3; 4 x 1
Thử lại trong tất cả các trường hợp x 2;3; 4 thoả mãn.
Vậy tp tất cả các số nguyên x thoả mãn yēu cà̀u là 2;3; 4 Bài toán 3
Câu 3 ( 1,0 điểm) Một cōng ty vặn tải Y đự dịnh sử dụng một đoàn xe để chở 80 tấn hàng hoá. Trước
khi khởi hành, do phát sinh cōng ty Y phải chở thēm 4 tấn hàng nữa, vì thế cōng ty đã điều thēm 2 xe
cùng tham gia vặn chuyển nēn tất cả các xe đều chờ giảm đi 1 tấn hàng so với ban đầu. Hỏi ban đầu
cōng ty Y dự định sử dụng bao nhiēu xe, biết rằng tất cả các xe cōng ty sử dụng đều cùng chủng loại và chở cùng khối lượng? Lời giải.
Gọi số xe ban đầu cõng ty Y định sử dụng là x (chiếc), ( * x N )
Vì ban đầu chờ 80 tấn hàng hoá nẽn số hàng hoá mỗi xe định chở là 80 (tấn) x
Thực tế, do phải chở thēm 4 tấn hàng nữa nẽn tổng phải chở là 80 + 4 = 84 (tấn) Trang 6
Sau khi điều thêm 2 xe, tổng số xe chở hàng là x + 2 (chiếc)
Khi đó, số hàng hoá thực tế mỗi xe phải chở là 84 (tấn) x + 2
Do mỗi xe chở giảm đi 1 tấn hàng so với ban đầu nẽn ta có phương trình sau: 80 84 −1 = x x + 2 80 − x 84 = x x + 2
(80− x)(x + 2) = 84x 2
x + 6x −160 = 0
(x −10)(x +16) = 0 Do *
x N nèn x +16 0 do đó x −10 = 0 hay x = 10 (thoả mãn)
Vậy ban đầu công ty Y định sử dụng 10 chiếc xe. Bài toán 4 Câu 4 ( 1,5 điểm)
1. Điều tra thời gian tự học của 20 học sinh trong một ngày, thu được bảng tần số sau:
Thời gian tự học (giờ) 1 2 3 4 5 Cộng Tån số (n) 5 4 6 3 2 N = 20
a , Lập bảng tần số tương đối của bảng tần số trèn.
b , Tính tỉ lệ phần trăm số học sinh có thời gian tự học ít nhất 3 giờ trong mọ̃t ngày.
2. Một hộp có 20 chiếc thẻ cùng loại, mỗi chiếc thẻ được ghi một trong các số 1, 2,3,, 20 ; hai thẻ khác
nhau được ghi hai số khác nhau. Rút ngẫu nhiên một chiếc thẻ trong hộp trên và quan sát số ghi trên thẻ
đó. Tính xác suất của biến cố A : "Số ghi trên chiếc thẻ rút được chia hết cho cả 2 và 3 Lời giải. 1. a ,
Mẫu số liệu đã cho có 5 giá trị khác nhau về thời gian tự học là 1;2;3;4;5 (giờ)
Các giá trị lần lượt có tần số là n = 5, n = 4, n = 6, n = 3, n = 2 và tổng N = 20 1 2 3 4 5
Do đó tần số tương đối của từng dữ liệu là Trang 7 5 25 f = = = 25% 1 20 100 4 20 f = = = 20% 2 20 100 6 30 f = = = 30% 3 20 100 3 15 f = = = 15% 4 20 100 2 10 f = = = 10% 5 20 100
Nên ta có bảng tần số tương đối
Thời gian tự học (giờ) 1 2 3 4 5 Cộng Tån số tương đối (%) 25 20 30 15 10 100
b , Để tự học ít nhất 3 giờ trong ngày thì phải học 3,4 , hoặc 5 giờ trong ngày
Từ bảng tần số tương đối, ta có tỉ lệ phần trăm của số học sinh tự học ít nhất 3 giờ trong ngày là: 30% +15% +10% = 55%
Vậy tỉ lệ phần trăm của số học sinh tự học ít nhất 3 giờ trong ngày là 55%
2. Trước hết ta có nhận xét: Một số chia hết cho cả 2 và 3 , mà 2 và 3 nguyēn tố cùng nhau nên số đó sẽ chia hết cho 6
Số phần tử của khōng gian mẫu là n(Ω) = 20 (Chọn ngẫu nhiēn một số trên một chiếc thẻ bất kì)
Các số chia hết cho 6 từ 1 tới 20 là: 6,12,18
Ta thấy từ 1 tới 20 có 3 số chia hết cho 6
Do đó số phần tử của biến cố A là n( A) = 3 n A
Vậy xác suất của biến cố 3
A là P ( A) ( ) = = = n( ) 0,15 Ω 20 Bài toán 5
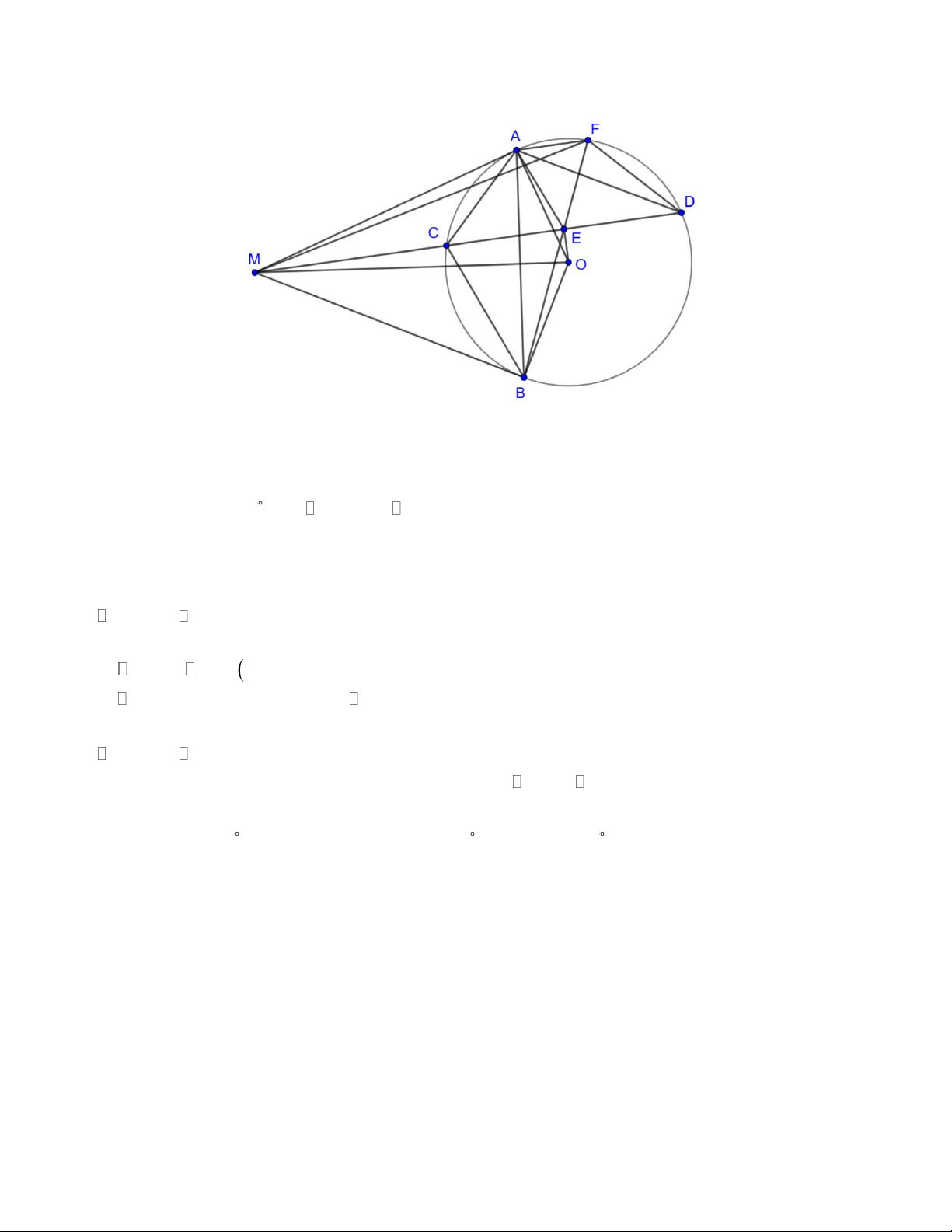
Câu 5(3,0 điểm) Cho đường tròn (O; R) và điểm M nằm ngoài (O) . Từ điểm M kẻ hai tiếp tuyến M ,
A MB với (O)( ,
A B là hai tiếp điểm). Xét điểm D thuộc cung lớn AB ( D không nằm chính giữa Trang 8
cung AB ), đường thẳng MD cắt (O) tại điểm C . Gọi E là trung điểm của dây CD , tia BE cắt đường
tròn (O) tại điểm F
1. Chứng minh bốn điểm M , ,
A O, B cùng thuộc một đường tròn.
2. Chứng minh hai tam giác EBC và EDF đồng dạng.
3. Chứng minh EM là tia phân giác của AEB
4. Khi D thay đổi trèn cung lớn AB , tìm vị trí của D để diện tích tam giác MDF lớn nhất. Lời giải.
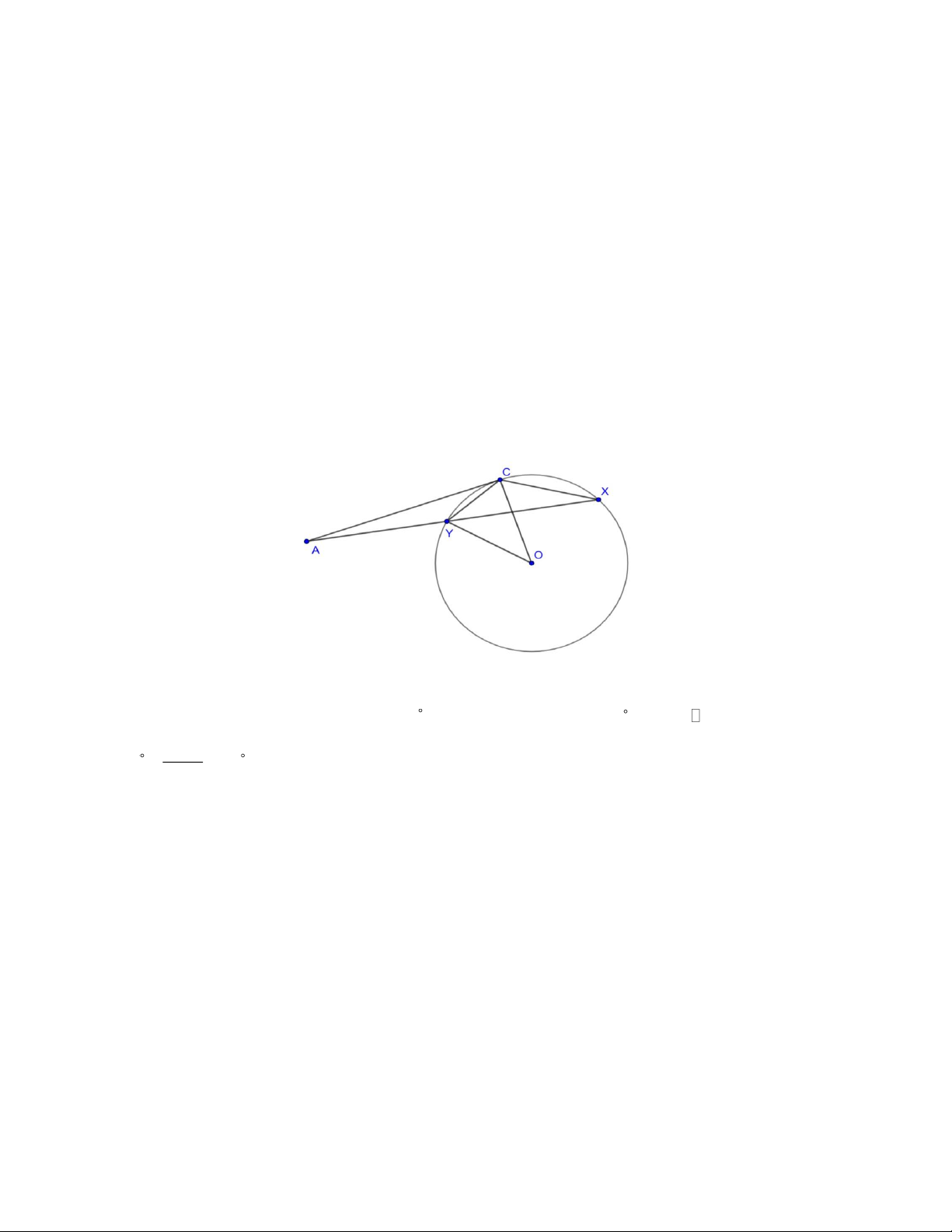
Bổ đề: Cho đường tròn (O), điểm A nằm ngoài đường tròn. Từ A kẻ tiếp tuyến AC với (O)(C là tiếp
điểm), kẻ cát tuyến AYX với đường tròn (O). Khi đó ACY = CXY Chứng minh
Do AC là tiếp tuyến của (O) nēn ACO = 90 dẫn tới ACY +YCO = 90 ( )
1 Do OCY cän tại O nèn COY OCY = 90 − = 90 − CXY (2) 2
Từ (1), (2) ta có ACY = CXY Trở lại bài toán Trang 9 1. Do M ,
A MB là tiếp tuyến tại ,
A B với (O)(GT) nên MA ⊥ , OA MB ⊥ OB
Do đó MAO = MBO = 90 nēn MAO và MBO đều nội tiệp đường tròn đường kính MO Suy ra , A B
thuộc đường tròn đường kính MO nên M ,O, ,
A B cùng thuộc đường tròn đường kính MO (dpem)
2. Xét (O) có BCD = BFD (2 góc nội tiếp cùng chấn cung BD của (O) )
Xét EBC và EDF có
CEB = FED (2 góc đối dỉnh), ECB = EFD (cmt)
Do đó EBC ∽ EDF (g.g )
3. Xét OCD có OC = OD = R nên OCD cản tại O
E là trung điểm CD (GT) nēn CE = ED
Xét OEC và OED có:
OC = OD ( cmt),OCE = ODE ( cmt),CE = ED( cmt ) Nèn OEC = OED (c.g.c) suy ra OEC = OED (2 góc tương ứng)
Mà OEC + OED = 180 (2 góc kề bù) nèn OEC = 90 hay OEM = 90
Suy ra E thuộc đường tròn đường kính MO
Từ đó có 5 điểm M , ,
A O, E, B cùng thuộc đường tròn đường kính MO
Xét đường tròn đường kính MO : Do MA = MB (Vi M ,
A MB là 2 tiếp tuyến) nên 2 cung MA và MB
bằng nhau (liên hệ giữa cung và dây)
Nên AEM = BEM (Góc nội tiếp chắn 2 cung bằng nhau)
Do đó EM là phân giác trong của AEB 4. Do M ,
A MB là tiếp tuyến của (O) nēn MAB = AFB (áp dụng bổ đề đã chứng minh) Trang 10
Mà MAB = MEB nên MEB = AFB, 2 góc này ờ vị trí đồng vị suy ra AF / /CD Ta có 1 S
= MD d F MD = MD d A MD = S MFD ( ) 1 , ( , ) 2 2 MAD Lai có 1 1 S
= AM AD sinMAD„ AM 2R 1 = AM R MAD 2 2 Do ,
A M cố định nên AM không đổi do vậy S „ AM .R MFD
Dấu "=" xảy ra khi: sinMAD = 1 và AD là đường kính (O) từ đó suy ra ,
A O, D thẳng hàng.
Vậy khi D là giao điểm thứ hai của AO với (O) thì S
đạt giá trị lớn nhất là AM .R MFD Bài toán 6 Câu 6 ( 1,0 điểm)
1. Hình 1 mô tả ba địa điểm nằm ở ba vị trí là ba đỉnh của tam giác ABC vuông tại A . Do điều kiện
thực tế không đo được trực tiếp khoảng cách từ B đến C , nhưng đo được AB = 200 m và
ABC = 30 . Tính khoảng cách BC (kết quả làm tròn đến hàng đơn vị của mét).
2. Trường THCS X đang khảo sát điểm làm một vườn thực nghiệm hình chữ nhặt MNPQ trên khu
đất dạng tam giác ABC vuông tại A nằm trong góc khuôn viên nhà trường (như hình 2), với
AB = 6 m, AC = 8 m . Biết rằng chi phí làm 2
1 m vườn thực nghiệm là 1,2 triệu đồng, hỏi nhà
trường cần chi bao nhiēu triẹ̉u đồng để diện tích khu vườn làm được là lớn nhất? Trang 11 Lời giải. 1. Xét AB AB
ABC là tam giác vuông tại A , cạnh huyền BC nên cosB = hay = cos30 Do đó BC BC AB 200 BC = = = 231( m) cos30 3 2 Vậy BC = 231 m 2.
Kẻ đường cao AH của ABC
Theo định lý Pytago cho ABC vuông tại A ta có 2 2
BC = AB + AC = 10( m) Ta có 1 1 1 1 1 : = + = +
nên AH = 4,8(m) 2 2 2 2 2 AH AB AC 6 8
Theo hệ quả định lý Thales cho AHC có NP / / AH ta được NP CP = AH AC Do đó AH 3 NP = CP = CP AC 5
Tương tự theo hệ quả định lý Thales ta có QP AP = nên BC 5 QP = AP = AP BC AC AC 4 Ta có 3 5 3 S = Q .
P NP = CP AP = A . P CP MNPQ 5 4 4
Áp dụng bắt đẳng thức AM-GM ta được: 2 2 (AP + CP) AC AP CP„ = =16 4 4 Do đó 3 S „ .16 = 12 MNPQ ( 2 m ) 4
Dấu "=" xảy ra khi: AP = CP = 4(m) vì vậy cần chi 12.1,2 =14,4 (triệu đồng)
Vậy cần phải chi 14,4 triệu đồng để diện tích khu vườn làm được lớn nhất. Trang 12




