Đề Tuyển Sinh 10 Môn Toán Sở GD Lào Cai 2025-2026 Có Đáp Án

SỞ GIÁO DỤC VÀ ĐÀO TẠO LÀO CAI
KÌ THI TUYỂN SINH VÀO LỚP 10 THPT
ĐỀ THI CHÍNH THỨC NĂM HỌC 2025-2026
(Đề thi gồm có 2 trang)
Môn thi: Toán ( không chuyên )
Thời gian làm bài:120 phút, không kể thời gian giao đề
Ngày thi:04 tháng 6 năm 2025
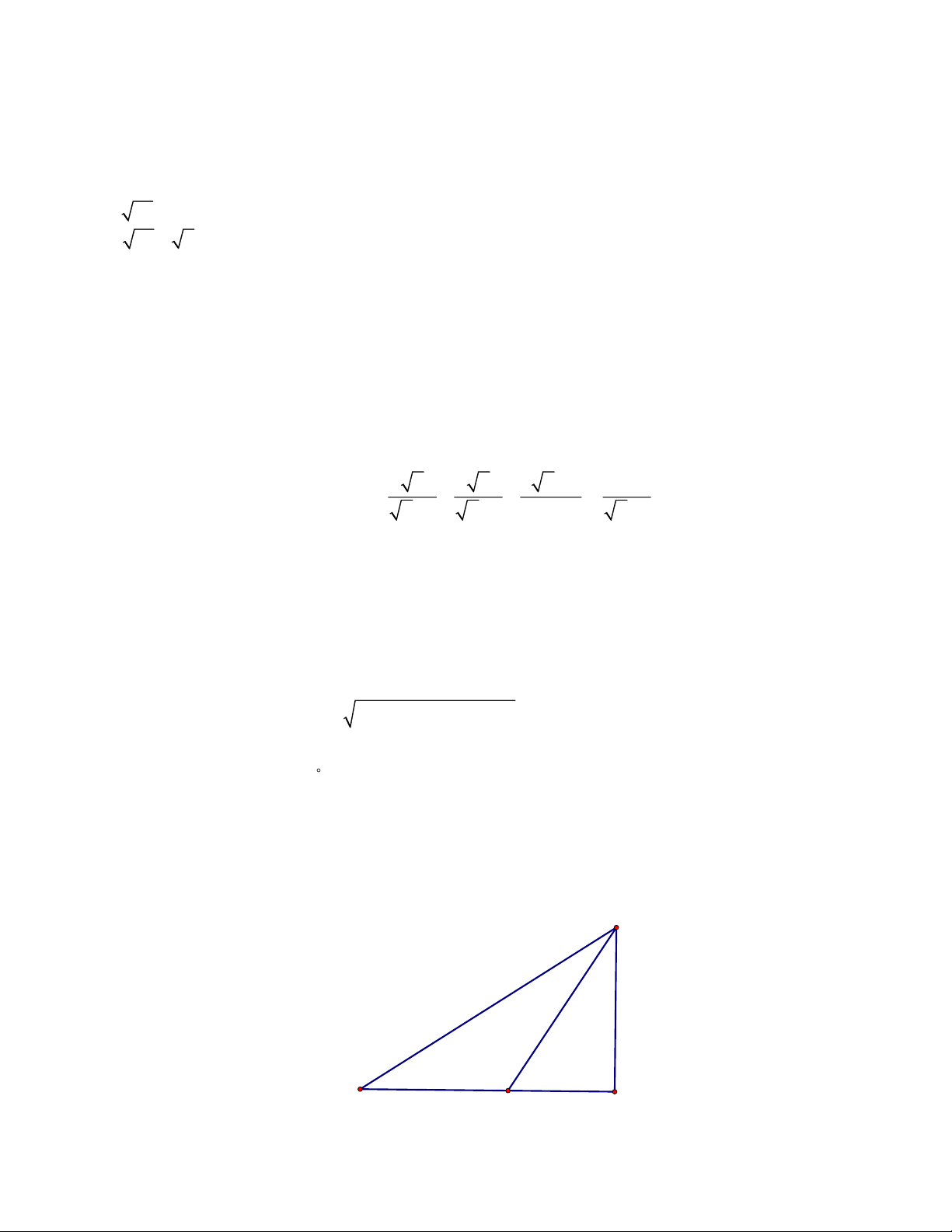
Câu 1 ( 1,0 điểm). Tính giá trị các biểu thức sau: a) A = 64 . b) B = 36 − 4 .
Câu 2 ( 1,0 điểm). Giải phương trình: 2
x + 5x + 6 = 0 . x − 2y = 8
Câu 3 ( 1,0 điểm). Giải hệ phương trình:  2x + 3y = 5 −
Câu 4 ( 1,0 điểm). Có chín tấm thẻ lần lượt ghi các số 1;2;3;4;5;6;7;8;9 . Bạn Cường rút ngẫu nhiên
một tấm thẻ từ trong hộp chứa chín tấm thẻ đó.
a) Tính số phần từ của không gian mẫu.
b) Tỉnh xác suất của biến cố A : "Rút được tấm thẻ ghi số chã̃n".  a a 2 a − 4  1
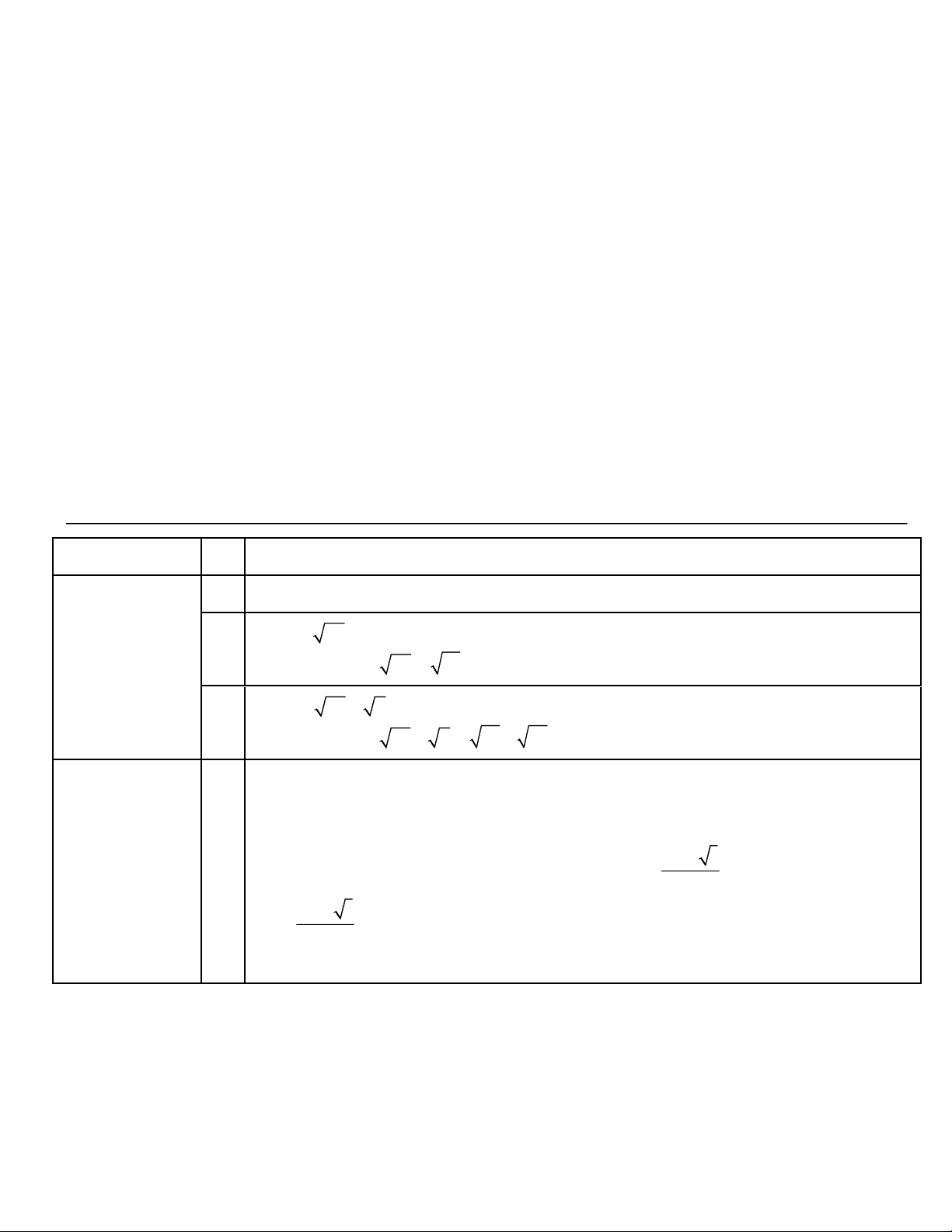
Câu 5 (1,0 điểm). Cho biểu thức M =  − +  : 
với a  0, a  1 a +1 a −1 a 1  − a −1  
a) Rút gọn biểu thức M .
b) Tìm các giá trị của a để M  −2.
Câu 6(0,5 điểm). Tổng số học sinh của hai lớp 9 A và 9 B là 83 học sinh. Trong đợt ủng hộ vở cho các
bạn học sinh vùng lũ, mỗi học sinh lớp 9A ủng hộ 4 quyển vở, mỗi học sinh lớp 9B ủng hộ 3 quyển vở
nên cả hai lớp ủng hộ được 289 quyển vở. Hỏi mỗi lớp có bao nhiêu học sinh?
Câu 7 ( 0,5 điểm). Cho phương trình 2
x − 5x + 2 = 0 có hai nghiệm là x , x . Không giải phương trình, 1 2
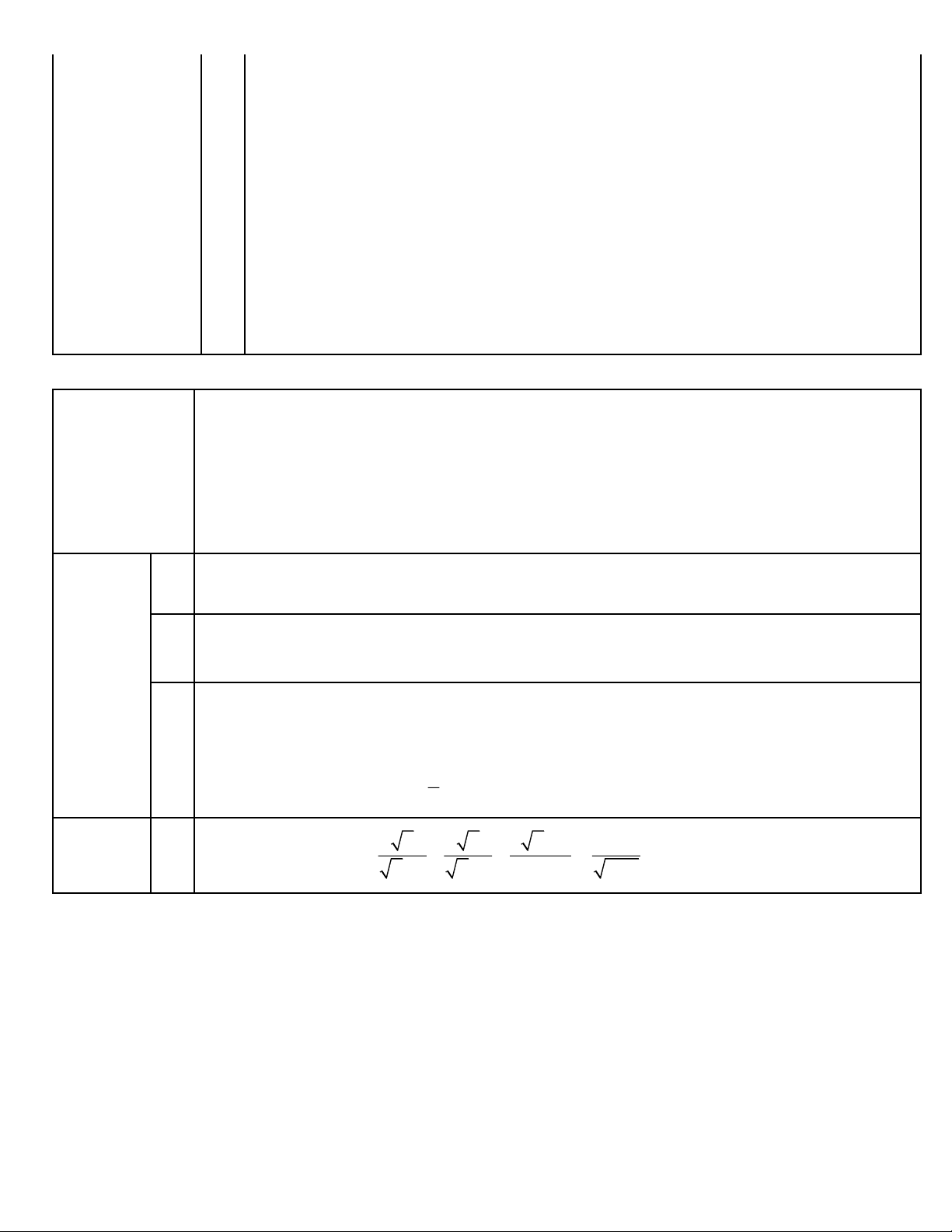
hãy tính giá trị của biểu thức: 2 A = 16x 8
+ x x + 5x − 2 + 3x . 1 1 2 2 2
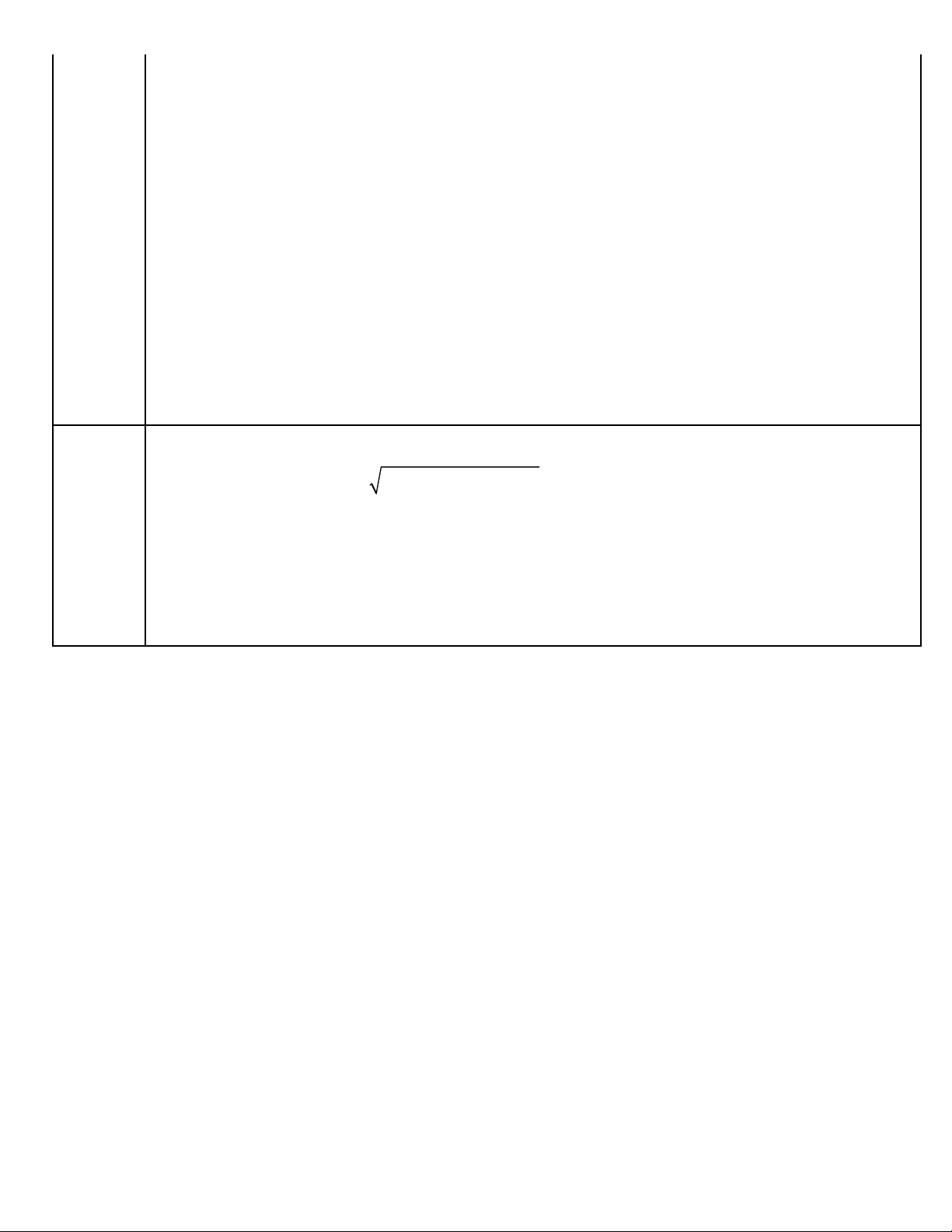
Câu 8(1,0 điểm). Hình vẽ bên mô tả tia nắng mặt trời dọc theo AC tạo với phương nằm ngang trên
mặt đất một góc ACB bằng 60 . Khi đó, người ta đo được bóng của một cái tháp trên mặt đất là đoạn
thẳng BC dài 30 m . Biết tháp có phương vuông góc với mặt đất.
a) Tính chiều cao AB của tháp (làm tròn kết quả đến hàng phần trăm).
b) Tại một thời điểm khác, người ta đo được bóng cùa A 60° D C B Trang 1
tháp có độ dài BD = 90 m . Tính góc ADB giữa tia nắng mặt trời và mặt đất vào thời điểm đó.
Câu 9 ( 1,0 điểm). Một cốc nước hình trụ có bán kính đáy phía trong thành cốc là 4 cm đang chứa
nước nhưng chưa đầy. Người ta thả chìm hoàn toàn vào cốc 3 viên bi hình cầu giống hệt nhau thì thấy
mực nước trong cốc dâng lên nhưng chưa đầy cốc. Biết bán kính mỗi viên bi bằng 2 cm .
a) Tính thể tích của mỗi viên bi.
b) Sau khi thả chìm hoàn toàn vào cốc 3 viên bi thì thấy chiều cao của mực nước trong cốc dâng lên so
với mực nước ban đầu là h( cm) . Tính h .
Câu 10 (2,0 điểm). Cho tam giác ABC nhọn (AB  AC) nội tiếp đường trờn (O) . Ba đường cao
AD, BE,CF của tam giác ABC cắt nhau tại H .
a) Chứng minh bốn điểm C, E, H, D cùng thuộc một đường tròn.
b) Kẻ đường kính AM của đường tròn (O) . Chứng minh AD  MC = AC  BD .
c) Gọi P là giao điểm của AH và EF; I là giao điểm của AM và BC; K là trung điểm của BC . Chứng
minh: K là trung điểm của HM và PI song song với HK .
HƯỚNG DẪN GIẢI CHI TIÉT ĐỀ THI VÀO 10 NĂM HỌC 2025-2026 MÔN TOÁN - LÀO CAI
THỰC HIỆN: BAN CHUYÊN MÔN TUYENSINH247.COM Câu Ý
Hướng dẫn giải của Tuyensinh247.com
Tình giá trị biểu thức sau: a) A = 64 Câu 1: (1 a) Cách glảl: 2 A = 64 = 8 = 8 đlểm) b) B = 36 − 4 b) Cách giải: 2 2
B = 36 − 4 = 6 − 2 = 6 − 2 = 4 Giai Pharong trinh 2
x + 5x + 6 = 0 . Cách glải: Ta có: 2
Δ = 5 − 4.1.6 = 25 − 24 = 1  0 Câu 2: (1 5 − + 1
Suy ra phương trình có hai nghiệm phân biệt x = = 2 − và đlểm) 1 2.1 5 − − 1 x = = 3 − 2 2.1
Vậy phương trình có hai nghiệm x = −2 và x = −3 . 1 2 Trang 2 x − 2y = 8
Giải hệ phương trình:  2x + 3y = 5 −  x − 2y = 8  2x + 3y = 5 − Cách glải: Câu 3: (1  x = 8 + 2y  đlểm) 2x + 3y = 5 − x = 8 + 2y x = 8 + 2y  
2(8 + 2y) + 3y = 5 −  7y = 2 − 1 x = 8 + 2y  y = 3 − x = 8 + 2.( 3 − )   y = 3 −  x = 2  y = 3 −
Vậy hệ phương trình có nghiệm ( ; x y) = (2; 3 − ) .
Có chín tấm thẻ lần lượt ghi các số 1; 2; 3; 4; 5; 6; 7; 8; 9. Bạn Cường rút ngẫu nhiên
một tấm thẻ từ trong hộp chứa chìn tẩm thẻ đó.
a) Tinh số phần tử của không gian mẫu a)
Cách glải: Không gian mẫu của phép thử là: Ω = 1;2;3;4;5;6;7;8;  9 gồm 9 phần tử. Câu 4: (1 điểm)
b) Tính xác suất của biến cố A: "Rút được tấm thẻ ghi số chẵn" Cách glải:
b) Có 4 kết quả thuận lợi cho biến cổ A là 2;4;6;8
Xác suất của biến cố A là: 4 . 9 Câu 5:  a a a −  Cho biếu thirc 2 4 1 M =  − +  :
với a  0, a  1 (1 đlểm)  a +1 a −1 a 1  − a −1   Trang 3
a) Rüt gọn biểu thừc M . Cách gläl:  −  Với a a a
a  0, a  1 ta có: 2 4 1 M =  − +  :  a +1 a −1 a 1  − a −1    a ( a − ) 1 a ( a + ) 1  2 a − 4 1 M  (  = − +  a + ) 1 ( a − ) 1
( a + )1( a − )1 ( a + )1( a −  ) : 1  a −1  a) a ( a − ) 1 − a ( a + ) 1 + 2 a − 4 M = (  − a + )( a − ) ( a )1 1 1
a − a − a − a + 2 a − 4 − M = 4 M = a +1 a +1 4 − Vậy M =
vói a  0, a  1 a +1
b) b) Tim các giá tri của a để M > -2 Cách giải:
ĐK: a  0, a  1 M  −2 4 −  2 − a +1 2 1 a +1 a +1  2 a  1 a  1
Kết hợp điều kiện ta được: a  1 là giá trị cần tìm. Trang 4
Tổng số học sinh của hai lớp 9A và 9B là 83 học sinh. Trong đột ủng hộ vở cho các bạn
học sinh vùng lū, mỗi học sinh lởp 9A ủng hộ 4 quyển vở, mỗi học sinh lởp 9B ủng hộ 3
quyển vở nên cả hai lớp ủng hộ được 289 quyển vở. Hỏi mỗi lớp cỏ bao nhiêu học sinh? Cách giải
Gọi x, y (học sinh) lần lượt là số học sinh của lớp 9 A và lớp 9 B với x, y  83, x, y  N
Tổng số học sinh của hai lớp 9 A và 9 B là 83 học sinh nên ta có: x + y = 83 Câu 6:
Trong đợt ùng hộ vở cho các bạn học sinh vùng lū, mỗi học sinh lớp 9A ủng hộ 4 quyển vở, (0,5
mỗi học sinh lớp 9 B ủng hộ 3 quyển vở nên cả hai lớp ủng hộ được 289 quyển vở, nên ta dlểm)
có: 4x + 3y = 289 x + y = 83
Theo đề bài ta có hệ phương trình:  4x + 3y = 289 x = 40
Giài hệ phương trình ta được  (tmđk) y = 43
Vậy lớp 9A có 40 học sinh, lớp 9B có 43 học sinh. Cho phương trình 2
x − 5x + 2 = 0 có hai nghiệm là x , x . Không giäi phương trình, hãy tình 1 2
giá trị cùa biểu thức: 2
A = 16x + 8x x + 5x − 2 + 3x . 1 1 2 2 2 Câu 7: Cách giải (0,5 x + x = 5 2 − + = đlểm) x
5x 2 0 có hai nghiệm x , x . Theo Viete, ta có 1 2 1 2 x x = 2  1 2
Suy ra hai nghiệm x  0, x  0 . 1 2
Vì x là nghiệm của phương trình 2
x − 5x + 2 = 0 , nên ta có: 2 Trang 5 2
x − 5x + 2 = 0 suy ra 2 5x − 2 = x 2 2 2 2 Thay 2
5x − 2 = x vào biều thức trong dấu căn: 2 2 2
16x + 8x x + 5x − 2 1 1 2 2 2 2
= 16x + 8x x + x 1 1 2 2
= (4x )2 + 2(4x ) x + ( x )2 1 1 2 2 = (4x + x )2 1 2
Suy r 16x + 8x x + 5x − 2 = (4x + x )2 2 = 4x + x . 1 1 2 2 1 2 1 2
Do đó biểu thức A trở thành: A = 4x + x + 3x 1 2 2
Vì x  0 và x  0 , nèn 4x + x  0 . 1 2 1 2
Suy ra 4x + x = 4x + x . 1 2 1 2
A = (4x + x + 3x 1 2 ) 2
A = 4x + 4x
Thay vào biểu thức A , ta được 1 2
A = 4( x + x 1 2 ) A = 4.5 = 20
Vậy giá trị của biều thức A là 20 .
Hinh vē bên mô tả tia nắng mặt trời dọc theo AC tạo vởi phương nằm ngang trên mặt
đất một góc  ACB bằng 60 . Khi đó, người ta đo được bóng của cải thảp trên mặt đất
là đọan BC đài 30 m . Biết tháp có phương vuông góc vởi mặt đất.
a) Tính chiều cao AB cua thảp (làm tròn kết quả đến hàng phần trãm). Câu 8: Cách giải: (1
Xét ABC vuông tại B , áp dụng tỉ số lượng giác ta có: đlểm) a) AB tan ACB = CB
Suy ra: AB = tan A .
CB BC = tan60 .30 = 30 3  51,96( m)
b) Tại một thời điểm khảc, ngırời ta đo được bóng của tháp cỏ độ dài BD = 90 m . Tính
b) góc giữa  ADB giữa tia nẳng mặt trời và mặt đất vào thời điểm đó. Cách giải: AB 30 3 3
Xét ABD vuông tại B ta có: tan ADB = = = DB 90 3 Suy ra  ADB = 30 .
Một cốc nước hinh trụ có bán kính đáy phía trong thành cốc là 4cm đang chứa nước Câu 9:
nhưng chıra đầy. Ngırời ta thả chìm hoàn toàn vào cốc 3 viên bi hình cầu giống hệt (1
nhau thi thấy mực nước trong cốc tãng lên nhưng chưa đầy cốc. Biết bán kính mỗi viên đlểm) bi bằng 2 cm . Trang 6
a) Tính thể tích mỗi viên bi. Cách giải: a) 
Thể tích mỗi viên bi là: 4 3 4 3 32  r =  2 = ( 3 cm ) 3 3 3
b) Sau khi thả chìm hoàn toàn vào cốc 3 viên bi thì thấy chiều cao của mực nước trong
cốc đâng lên so với mực nước ban đầu là h(cm). Tính h. Cách giải:
Thể tích nước dâng lên là: 2 2
 R h =  4 h =16 h
b) Vì thể tích nước tăng lên bằng thể tích 3 viên bi nên ta có: 32 16 h = 3. = 32 3 Suy ra h = 2( cm) Cho tam giác ABC nhọn (AB
CF của tam giác ABC cắt nhau tại H. Câu
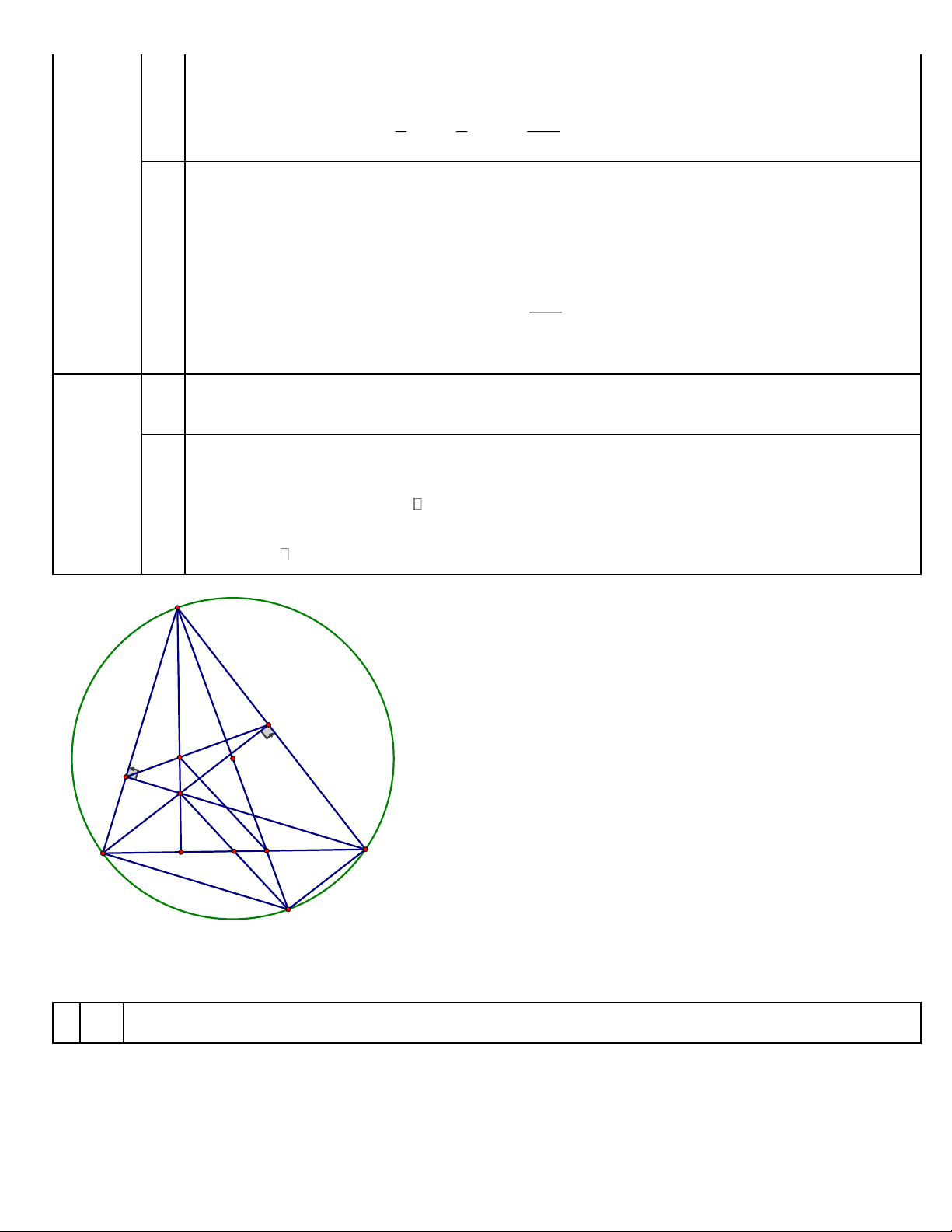
a) Chứng minh bốn điểm C, E, H, D cùng thuộc một đường tròn. 10: (2 Cách giải: đlểm) a)
Ta có AD ⊥ BC tại D nên HDC vuông tại D . Suy ra H, D,C cùng thuộc đường tròn đường kính HC .
Tương tự HEC vuông tại E nên H, E,C cùng thuộc đường tròn đường kính HC . A E P F O H I B D K C M
Vậy H, D,C, E cùng thuộc đường tròn đường kính HC . Trang 7
b) Kẻ đường kính AM của đường tròn (O). Chứng minh AD  MC = AC  BD . Cách giải:
Ta có  ACM = 90 (góc nội tiếp chắn nửa đường tròn) nên  ACM =  ADB
b) Lại có  ABD =  AMC (cùng chắn cung AC ) nên suy ra ABD  AMC( g.g) Suy ra AD BD =
hay AD  MC = AC  BD AC MC
c) Gọi P là giao điểm của AH và EF; I là giao điểm của AM và BC; K là trung điểm của BC.
Chứng minh: K là trung điểm của HM và PI song song với HK. Cách giải:
Do  ACM = 90 nên MC ⊥ AC . Mà BE ⊥ AC nên MC ‖ BE
Tương tự  ABM = 90 nên MB ⊥ AB . Mà CF ⊥ AB nên CF ‖ MB
Suy ra BHCM là hình bình hành
Mà K là trung điểm của BC nên K là trung điểm của HM
Do ABD  AMC (cmt) nên  BAD =  CAM . c)
Kết hợp với  AFE =  ACB (cùng cộng với  BFE bằng 180 )
Suy ra AFP − ACI ( g  g) . Khi đó AP AF = AI AC
Tương tự AFH − ACM ( g.g) nên AF AH = AC AM Suy ra AP AH = hay AP AI = AI AM AH AM
Suy ra PI ‖ HM (dpcm) Trang 8