Đề Tuyển Sinh 10 Môn Toán Trường Đại Học Khoa Học Huế 2025-2026 Có Đáp Án

TRƯỜNG ĐẠI HỌC KHOA HỌC
KỲ THI TUYỂN SINH LỚP 10
HỘI ĐỒNG TUYỂN SINH LỚP 10 THPT CHUYÊN
NĂM HỌC 2025 – 2026
ĐỀ THI CHÍNH THỨC
Ngày thi: 29 tháng 5 năm 2025
Môn thi: TOÁN (VÒNG 1)
Thời gian làm bài: 90 phút Câu 1.
a) Không sử dụng máy tính cầm tay, tính giá trị của biểu thức A = 18 − 50 + 8
b) Tìm điều kiện của x để biểu thức B = x − 2025 xác định x − x x −1
c) Rút gọn biểu thức C = + − x với x > 0 x x +1 Câu 2. Cho hàm số 2 y = 2
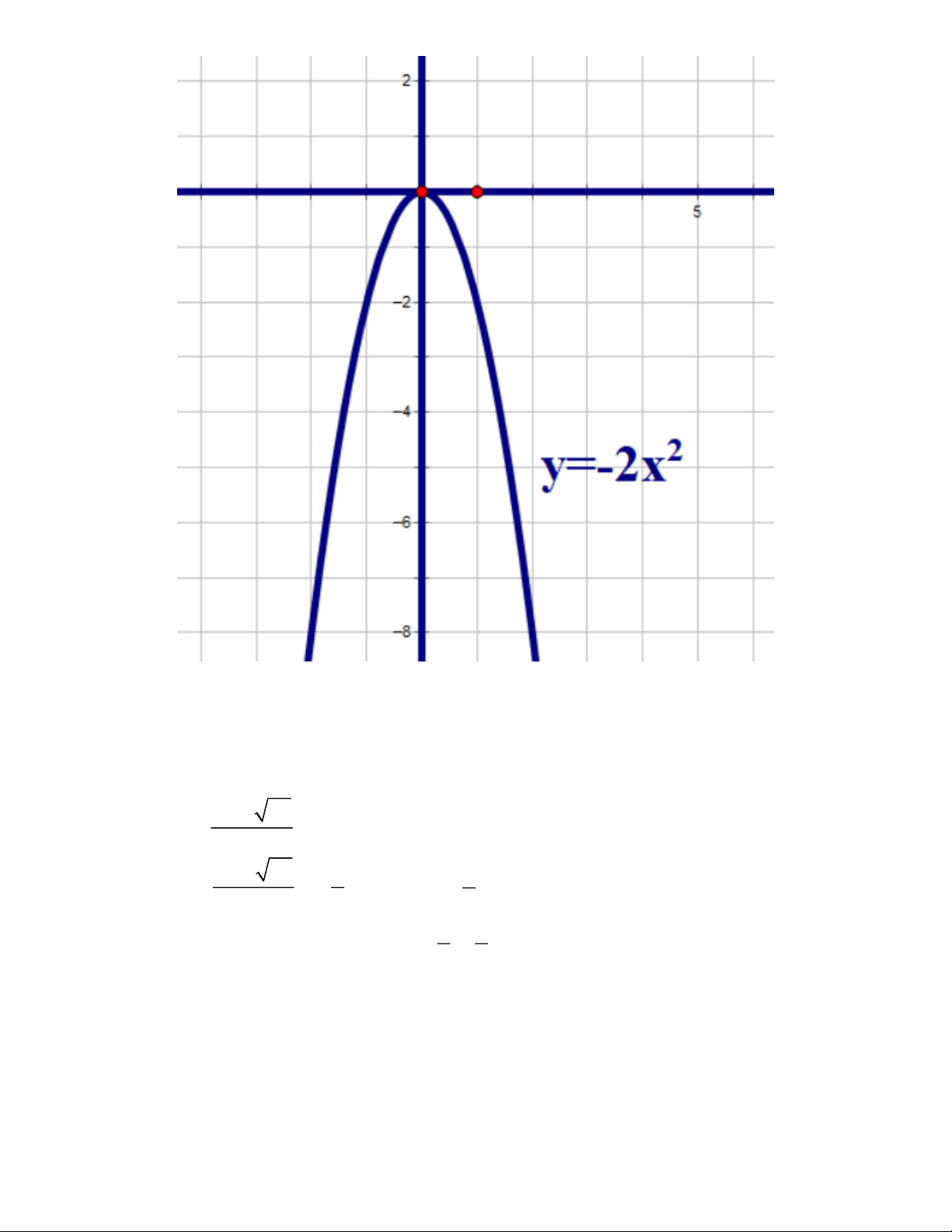
− x có đồ thị (P) và đường thẳng (d) : y = x − 3 a) Vẽ đồ thị (P)
b) Tìm tọa độ giao điểm của (P) và (d) bằng phép toán Câu 3. Cho phương trình 2 2x − 3x − 4 = 0 (1)
a) Chứng tỏ phương trình (1) có hai nghiệm phân biệt
b) Gọi x , x là hai nghiệm của phương trình (1). Không giải phương trình trên, 1 2 1 1
hãy tính giá trị của biểu thức M = + . 2 2 2(x −1) +1 2(x −1) +1 1 2
Câu 4. Để chuẩn bị cho năm học mới, bạn Lâm được mẹ cho 200 nghìn đồng để
mua bút và vỡ. Bạn Lâm đã mua 5 cây bút với giả mỗi cây là 8 nghìn đồng. Hỏi
với số tiền mẹ cho bạn Lâm có thể mua nhiều nhất bao nhiêu quyển vở, biết giá
mỗi quyển là 15 nghìn đồng?
Câu 5. Cho hai đường thẳng song song (d) và (d'). Trên đường thẳng (d) cho 3
điểm A, B, C phân biệt; trên đường thẳng (d) cho 2 điểm M, N phân biệt. Xét phép
thử “chọn ngẫu nhiên 3 điểm trong 5 điểm đã cho”.
a) Xác định không gian mẫu của phép thử.
b) Tính xác suất của biến cổ “ba điểm được chọn tạo thành tam giác có một đỉnh là A”.
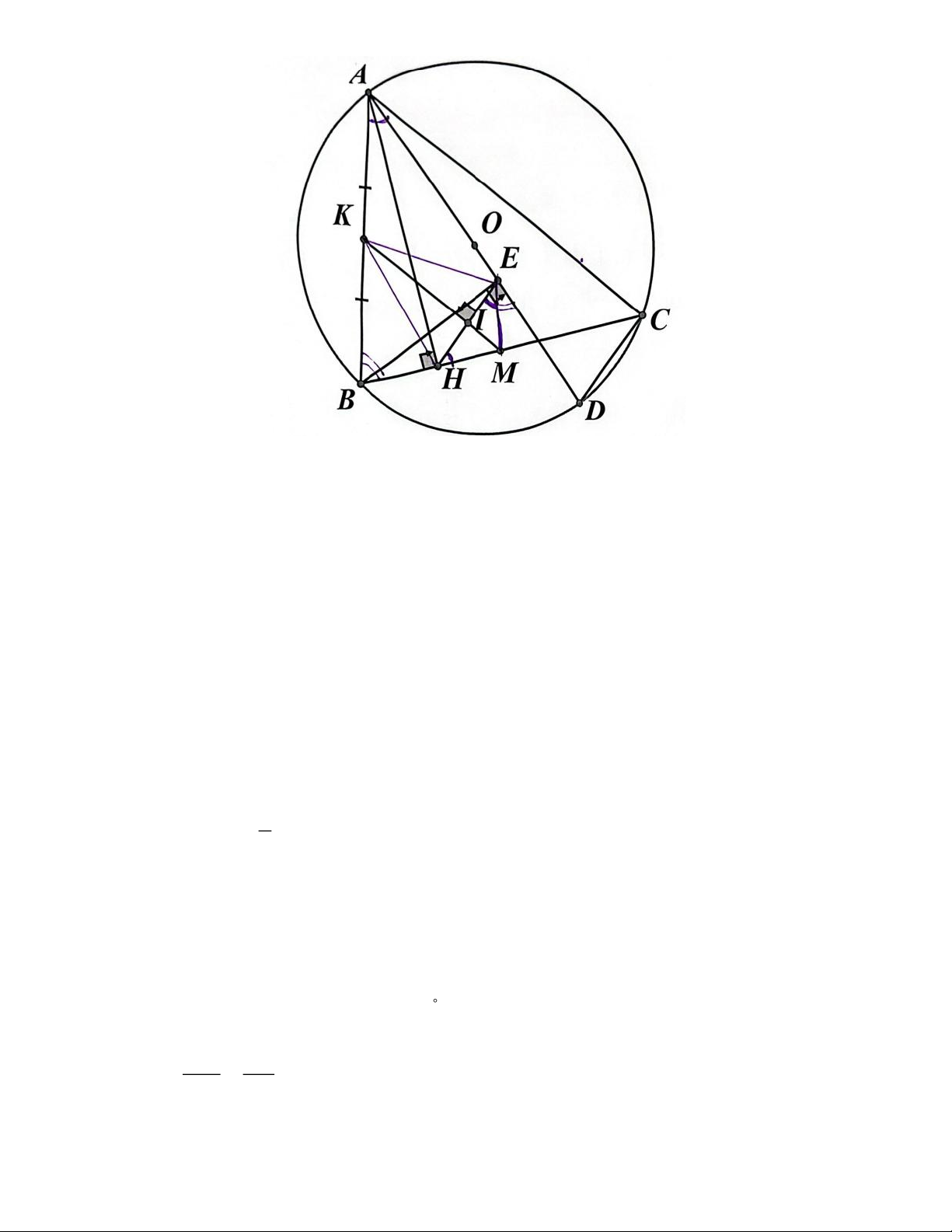
Câu 6. Cho tam giác nhọn ABC (AB < AC) nội tiếp đường tròn (O). Kẻ AH vuông
góc với BC tại H và BE vuông góc với đường kính AD của đường tròn (O) tại E.
a) Chứng minh tử giác ABHE nội tiếp đường tròn. b) Chứng minh HE // DC.
c) Gọi M, K lần lượt là trung điểm của BC và AB; I là giao điểm của KM và HE. AB.HE Tính . AE.HM
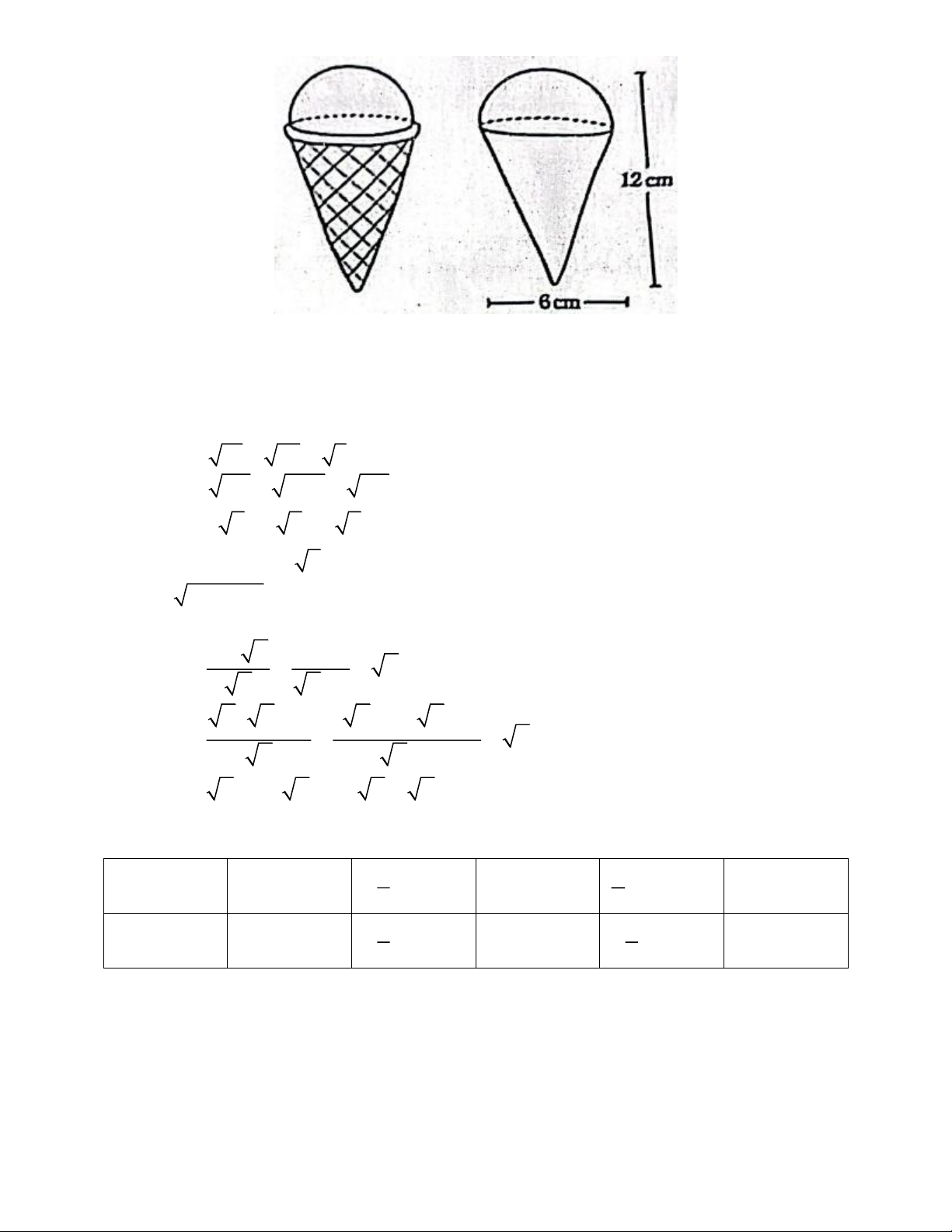
Câu 7. Một cây kem ốc quế gồm hai phần có kích thước như hình bên dưới
+ Phần bánh ốc quế có dạng hình nón, bên trong chứa kem
+ Phần kem úp lên trên miệng bánh là nửa hình cầu Trang 1
Tính thể tích kem thực tế có trong cây kem, biết lượng kem thực tế bằng 80% thể
tích của cây kem ốc quế (giả thiết phần bánh ốc quế có bề dày không đáng kể, kết
quả làm tròn đến hàng phần mười). ĐÁP ÁN Câu 1. a) A = 18 − 50 + 8 A = 9.2 − 25.2 + 4.2 A = 3 2 − 5 2 + 2 2 A = (3 − 5 + 2) 2 = 0
b) B = x − 2025 xác định khi x − 2025  0 Suy ra: x  2025 x − x x −1 c) C = + − x (x > 0) x x +1 x ( x − ) 1 ( x − )1( x + )1 = + − C x x x +1
C = x −1+ x −1− x = x − 2 Câu 2. a) 2 y = 2 − x x -1 1 − 0 1 1 2 2 2 y = 2 − x -2 1 − 0 1 -2 − 2 2 Trang 2
b) Ta có phương trình hoành độ giao điểm 2 −2x = x − 3 2 2x + x − 3 = 0 Có 2
 =1 − 4.2.(−3) = 25  0
Nên phương trình có hai nghiệm phân biệt 1 − + 25 x = =1 suy ra y = -2 1 4 1 − − 25 3 9 x = = − suy ra y = − 2 4 2 2  3 9 
Vậy tọa độ (P) và (d) là (1; -2) và − ;−   .  2 2  Câu 3. a) 2 2x − 3x − 4 = 0 (1) Có 2  = ( 3 − ) − 4.2.( 4 − ) = 41  0
Vậy phương trình (1) có 2 nghiệm phân biệt Trang 3  3 x + x =
Áp dụng hệ thức Viet ta có 1 2  2 x x = 2 −  1 2 Ta có: 2 2
2(x −1) = 2x − 4x + 2 = 3x + 4 − 4x + 2 = 6 − x 1 1 1 1 1 1 Tương tự suy ra 2 2(x −1) = 6 − x 2 2 1 1 1 1 Ta có: M = + = + 6 − x +1 6 − x + 2 7 − x 7 − x 1 2 1 2 7 − x + 7 − x 14 − (x + x ) 2 1 1 2 M = = (7 − x )(7 − x ) 49 − 7(x + x ) + x x 1 2 1 2 1 2 3 14 − 25 2 M = = 3 73 49 − 7. − 2 2 Câu 4.
Gọi x (quyển vở) là số vở nhiều nhất mua được (x  N*) Ta có bất phương trình: 8.5 +15x  200 15x 160 32 x  3 Mà x  N * nên x = 10.
Vậy mua được nhiều nhất 10 quyển vở. Bài 5. a) Không gian mẫu:
 = {ABC,AMN,BMN,CMN,ABM,ABN,BCM,BCN,ACM,ACN} Nên n = 10
b) Xét biến cố “Ba điểm được chọn tạo thành tam giác có A”
Tập hợp thuận lợi: {AMN,ABM,ACM,ACN} nên k = 4. k 4 2 P = = = . n 10 5 Câu 6. Trang 4
a) Tam giác AHB vuông tại H nên nội tiếp đường tròn đường kính AB (1)
Tam giác AEB vuông tại E nên nội tiếp đường tròn đường kính AB (2)
Từ (1) và (2) suy ra ABHE là tứ giác nội tiếp
b) Ta có: ABHE là tứ giác nội tiếp nên EHC = BAD (3)
mà BAD = MCD (góc nội tiếp cùng chắn cung BD) (4)
Từ (3) và (4) suy ra EHC = MCD
Mà hai góc này so le trong nên EH // CD
c) Tam giác BAC có K là trung điểm AB, M là trung điểm BC
nên KM là đường trung bình của tam giác ABC nên KM // AC (5)
Mà HE // CD (6) và CD ⊥ AC (7)
Từ (5), (6), (7) suy ra KM ⊥ HE
Lại có tam giác ABH vuông tại H và tam giác EAB vuông tại E 1
Nên KE = HE = AB (đường trung tuyến ứng với cạnh huyền) 2
Do đó K thuộc trung trực của HE (8)
Nên KM là đường trung trực HE, do đó HM = EM
Vậy tam giác HME cân tại M
Lại có EHM = BAE (AEHB nội tiếp) Xét  HIM và  AEB có BAE = IHM,AEB = HIM = 90
Suy ra:  HIM ~  AEB (g.g) HI AE Suy ra: = suy ra AE.HM = AB.HI HM AB Trang 5 AB.HE AB.2HI Vậy = = 2 . AE.HM AE.HM Câu 7. 6
Phần ống kem chóp có h =12 − r =12 − = 9(cm) 2 6
Phần kem úp nửa cầu có R = = 3(cm) 2 1 1 Thể tích phần ống kem: 2 2 3 V = r  h = . .  3 .9 = 27 (  cm ) 3 3 1 4 1 4 Thể tích phần kem úp: 3 3 3 V = . . R  = . . .  3 =18 (  cm ) 2 3 2 3
Thể tích thực tế lượng kem: 3 80%.(27 +18 )  113,1(cm ) Trang 6