Đề Tuyển Sinh 10 Toán Chung Sở GD Quảng Nam 2025-2026 Có Đáp Án

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH LỚP 10 THPT CHUYÊN QUẢNG NAM
Môn thi : TOÁN (Toán chung) ĐỀ CHÍNH THỨC
Thời gian : 120 phút (không kể thời gian giao đề)
Câu 1 (2,0 điểm). 2 2 + 2 + 3 + 6
a) Không sử dụng máy tính cầm tay, rút gọn biểu thức A = . 1+ 18 − 8 3 x − 21 2
b) Cho biểu thức B = +
, với x  0 và x  9 . x − 9 x − 3 5
Rút gọn B và tìm x để B = . 6
Câu 2 (2,0 điểm). 2x +3y =1
a) Không sử dụng máy tính cầm tay, giải hệ phương trình:  . x − y = 3 b) Cho parabol 2
(P): y =2x và đường thẳng (d): y =m ( m là tham số). Tìm giá trị của m
để (d ) cắt (P) tại hai điểm phân biệt A , B sao cho đoạn thẳng AB có độ dài bằng 2.
Câu 3 (2,0 điểm). a) Giải phương trình 4 2
2x − 3x − 2 = 0 .
b) Tìm tất cả các giá trị của tham số m để phương trình 2 2
x − 2mx + m − 3m + 2 = 0 có x x hai nghiệm phân biệt 1 x , 2 x thỏa mãn 1 2 + = 16 . 2 x 1 x
Câu 4 (3,5 điểm).
Cho đường tròn (O) đường kính AB = 2a , H là trung điểm của đoạn thẳng . OA Đường
thẳng d vuông góc với OA tại H và cắt đường tròn (O) tại hai điểm C, . D
a) Tính độ dài đoạn thẳng CD theo . a
b) Lấy điểm E trên cung nhỏ BD của đường tròn (O) sao cho ba điểm C, O, E không
thẳng hàng ( E khác B , E khác D ). Gọi M, N lần lượt là trung điểm của AC và CE; K là
hình chiếu vuông góc của A lên CE. Chứng minh BE song song với KH và MN là đường
trung trực của đoạn thẳng KH.
c) Gọi I, J lần lượt là trung điểm của BC và BD. Đường tròn đường kính AI cắt các
đoạn thẳng HB, AJ, HD lần lượt tại P, F, Q ( F khác A ). Gọi L là giao điểm của IF và PQ.
Chứng minh JL vuông góc với BD.
Câu 5 (0,5 điểm).
Cho ba số thực dương x, y, z thỏa mãn x + y + z = 3 . 2 y + yz
Tìm giá trị lớn nhất của biểu thức P = xy + 3xz + . 2
--------------- HẾT ---------------
Họ và tên thí sinh: ............................................................................................. Số báo danh: ...................................... Trang 1
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH LỚP 10 THPT CHUYÊN QUẢNG NAM HDC CHÍNH THỨC
HƯỚNG DẪN CHẤM MÔN TOÁN CHUNG
(Bản hướng dẫn này gồm 03 trang) Câu Nội dung Điểm Câu 1 2 2 + 2 + 3 + 6
(2,0) a) Không sử dụng máy tính cầm tay, rút gọn biểu thức A = . 0,75 1+ 18 − 8
2 2 + 2 + 3 + 6 = 2( 2 +1) + 3(1+ 2) = ( 2 +1)(2 + 3) 0,25 1+ 18 − 8 = 1+ 2 0,25 A = 2 + 3 0,25 3 x − 21 2
b) Cho biểu thức B = +
, với x  0 và x  9 . x − 9 x − 3 1,25
Rút gọn B và tìm x để 5 B = . 6
3 x − 21+ 2( x + 3) B =
( chỉ cần phân tích được x − 9 = ( x − 3)( x + 3) ) 0,25
( x − 3)( x + 3) − 5 x 15 = 0,25
( x − 3)( x + 3) 5 = 0,25 x + 3 5 5 5 B = 
=  x = 3  x = 9 0,25 6 x + 3 6
Đối chiếu điều kiện, x = 9 không thỏa. Vậy không có giá trị nào của x thỏa mãn yêu cầu. 0,25 Câu 2 2x +3y =1 (1)
(2,0) a) Không sử dụng máy tính cầm tay, giải hệ phương trình:  . 1,0
x − y = 3 (2) * Cách 1: * Cách 2:
Từ (2) suy ra: x = 3 + y (3)
Biến đổi hệ số của một phương trình 0,25
Thay (3) vào (1) ta được:
Cộng (trừ), tìm đúng giá trị một ẩn 0,25
2(3 + y) +3y =1  y = 1 − .
y = −1 x = 2 .
Tìm đúng giá trị ẩn còn lại 0,25
Vậy hệ phương trình đã cho có nghiệm là: Kết luận đúng ( ; x y) = (2; 1 − ) . ( ; x y) = (2; 1 − ) . 0,25 b) Cho parabol 2
(P) : y = 2x và đường thẳng (d) : y = m ( m là tham số). Tìm giá trị của m 1,0
để (d) cắt (P) tại hai điểm phân biệt A , B sao cho AB = 2 .
Phương trình hoành độ giao điểm của (P) và (d) là: 2 2x = m (1). 0,25
(d) cắt (P) tại 2 điểm phân biệt khi phương trình (1) có 2 nghiệm phân biệt, tức là m  0 . 0,25
Với m  0 , (1)  x =  m / 2 . Suy ra (
A − m / 2;m), B( m / 2;m) . 0,25
AB = 2  2 m / 2 = 2  2m = 2  m = 2 (thỏa m  0 ). Vậy m = 2 là giá trị cần tìm. 0,25
Câu 3 a) Giải phương trình 4 2
2x − 3x − 2 = 0 (1) 1,0 (2,0) Đặt 2
t = x , t  0 . 0,25
Phương trình (1) trở thành 2
2t − 3t − 2 = 0 (2) 0,25
Giải phương trình (2) được: t = −1 / 2 (loại) hoặc t = 2 . 0,25
Với t = 2 suy ra được x =  2 . 0,25
b) Tìm tất cả các giá trị của tham số m để phương trình 2 2
x − 2mx + m − 3m + 2 = 0 có ... 1,0  ' = 3m − 2 . 0,25 Trang 2
Phương trình đã cho có 2 nghiệm phân biệt khi  '  0  m  2 / 3 . 0,25
Điều kiện để phương trình có 2 nghiệm phân biệt khác 0 là: m  2 / 3 và 2
m − 3m + 2  0 (1) Theo định lý Viet: 2 1 x + 2 x = 2 ; m 1 x 2
x = m − 3m + 2 . 0,25 1 x 2 x 2 2 2 + =16  1 x + 2 x =16 1 x 2 x  ( 1 x + 2 x ) −18 1 x 2 x = 0 2 x 1 x 2 2 2
 (2m) −18(m − 3m + 2) = 0  7m − 27m +18 = 0  m = 3 hoặc 6 m = (thỏa (1)). 7 0,25
Vậy m = 3 hoặc m = 6 / 7 .
(nếu học sinh không có 2 điều kiện của (1) – trừ 0,25 và chấm tiếp)
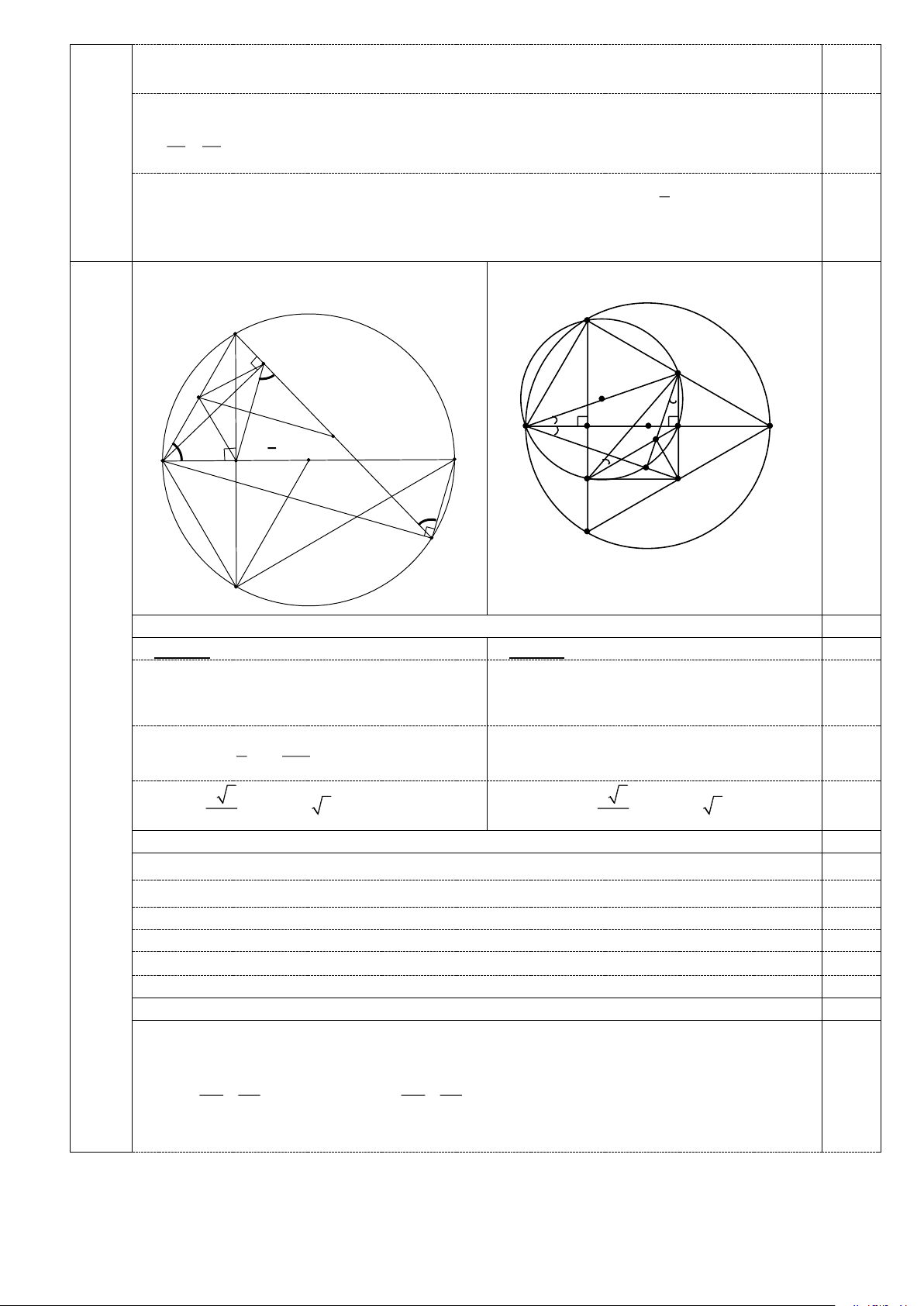
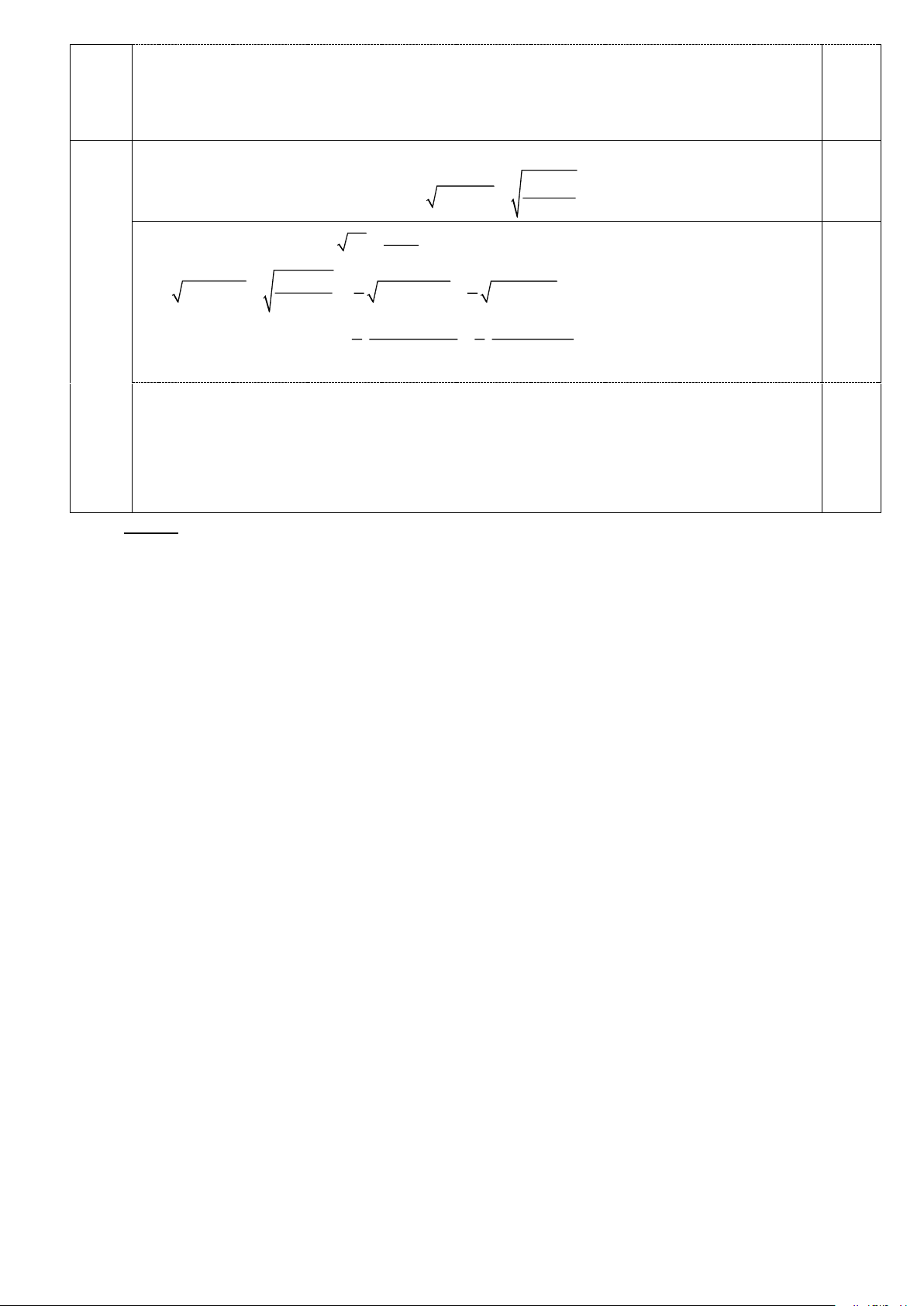
Câu 4 Hình vẽ phục vụ câu a: 0,25, câu b: 0,25 Hình vẽ câu c
(3,5) (không có hình không chấm) C C K I \ M = O / N A B a H L P 0,5 2 A B H O F Q J = a E D D
a) Tính độ dài đoạn thẳng CD theo . a 1,0
* Cách 1: CD = 2HD .
* Cách 2: CD = 2HD 0,25
+Tam giác OAD có OA = OD 2 2 2
HD = OD − OH .
+Vì H là trung điểm OA và DH ⊥ OA nên 0,25 DA = DO. 2 2  a  a 2 3 = a − =  
Suy ra  OAD đều. 0,25  2  4 a 3  a 3 HD =  CD = a 3 . Suy ra HD =  CD = a 3 . 0,25 2 2
b) Chứng minh BE song song với KH và MN là đường trung trực của đoạn thẳng KH. 1,5
Tứ giác AHKC nội tiếp trong đường tròn nên HKE=CAB . 0,25 Mà CAB=CEB nên HKE=CEB . 0,25
Do đó BE//KH (so le trong, B và H nằm về hai phía KE). 0,25 + AE//MN, BE//KH 0,25 + AE ⊥ BE nên MN ⊥ KH . 0,25
Mặt khác MH = MK nên MN là đường trung trực của đoạn thẳng KH. 0,25
c) Chứng minh JL vuông góc với BD . 0,5
+ IJ//CD và H là trung điểm của CD. Suy ra P là trung điểm của IJ.
Ta có: PIL=PAF=PAI=PQI và LPI=IPQ . Suy ra hai tam giác PIL và PQI đồng dạng. PI PL PJ PL Do đó: = . Mà PI = PJ nên = . 0,25 PQ PI PQ PJ
Lại có LPJ=JPQ nên hai tam giác PJL và PQJ đồng dạng (1). Trang 3
ABD=ACD=APQ  PQ//BD (đồng vị, tia PQ không nằm trong góc BPJ ).
Mà J là trung điểm của BD nên P là trung điểm của HB. Suy ra Q là trung điểm của HD. 0,25
Do đó JP ⊥ JQ hay tam giác PQJ vuông tại J (2).
Từ (1) và (2) suy ra tam giác PJL vuông tại L. Mà PQ//BD nên JL vuông góc với BD.
Câu 5 Cho ba số thực dương x, y, z thỏa mãn x + y + z = 3 . (0,5) 2 + 0,5
Tìm giá trị lớn nhất của biểu thức y yz
P = xy + 3xz + . 2 + + Áp dụng: a b
a,b  0 ta có ab 
, dấu bằng xảy ra khi a = b . 2 y( y + z)
P = x(y + 3z) + 1 1 =
4x( y + 3z) +
2y( y + z) 2 2 2 0,25 + + + +
1 4x (y 3z) 1 2y (y z)  . + .
= x + y + z = 3 . 2 2 2 2 Suy ra P  3.
4x = y + 3z 
2y = y + z P = 3  
 x = y = z =1.
x + y + z = 3  0,25
x  0; y  0;z  0
Vậy giá trị lớn nhất của P bằng 3 khi x = y = z =1. * Lưu ý:
+ Nếu thí sinh làm bài không theo cách nêu trong đáp án nhưng đúng thì vẫn cho đủ số điểm
từng phần như hướng dẫn quy định.
+ Không chấm những phần liên quan đến phần sai đứng trước. Trang 4