Đề Tuyển Sinh 10 Toán Chung Sở GD Quảng Nam 2025-2026 Có Đáp Án

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH LỚP 10 THPT CHUYÊN QUẢNG NAM
Môn thi : TOÁN (Toán chung) ĐỀ CHÍNH THỨC
Thời gian : 120 phút (không kể thời gian giao đề)
Câu 1. (2,0 điểm)
a) Không dùng máy tính bỏ túi, hãy rút gọn biểu thức A = ( 26 +5 2) 19 −5 13 . 2 x − x 3x − x b) Cho biểu thức B = − . x + x +1 x
Rút gọn B và tìm x để B = 1.
Câu 2. (2,0 điểm)
a) Cho parabol (P): y = ax2. Tìm hệ số a để đường thẳng (d): y = 2 cắt (P) tại hai
điểm A và B sao cho tam giác AOB vuông (với O là gốc tọa độ).
b) Tìm tham số m để phương trình 2
x + (m − 2) x − (m − )
1 (2m − 3) = 0 có hai nghiệm
phân biệt sao cho nghiệm này bằng bình phương nghiệm kia.
Câu 3. (2,0 điểm)
a) Giải phương trình ( − + )2 x 3 2 + x = 13 .  1 3 + = −2 x −2 y +1
b) Giải hệ phương trình  5 2  − = 7  x − 2 y +1
Câu 4. (3,5 điểm)
Cho tam giác ABC (AB > AC) ngoại tiếp đường tròn tâm I, gọi D, E, F lần lượt là
các tiếp điểm của đường tròn (I) với các cạnh BC, CA và AB. Các đường thẳng DE, DF lần
lượt cắt tia AI tại K và L, gọi H là chân đường cao hạ từ A xuống BC.
a) Giả sử số đo góc BAC bằng a0, hãy tính số đo góc BIC theo a0. b) Chứng minh BK // EF.
c) Gọi M là trung điểm của BC, chứng minh tứ giác KMLH nội tiếp.
Câu 5. (0,5 điểm)
Cho hai số thực x; y thỏa mãn 0  x  1, 0  y 1 và x + y = 3xy .
Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức 2 2 P = x + y − 4xy .
--------------- Hết ---------------
Họ và tên thí sinh: .................................................................................. Số báo danh: ..................................... Trang 1
HƯỚNG DẪN CHẤM MÔN TOÁN CHUNG
KỲ THI TUYỂN SINH LỚP 10 THPT CHUYÊN
(Bản hướng dẫn này gồm 02 trang) Câu Nội dung Điểm Câu a)
A = ( 26 +5 2) 19 −5 13 = ( 13 +5) 2 19 −5 13 0,25 1 (1,0) (2,0) ( + ) − = ( + ) ( − )2 A= 13 5 38 10 13 13 5 13 5 0,25 A = ( 13 +5)(5− 13) 0,25 A = 12 0,25 b) 2 x ( 3 ( x) − ) 1 (1,0) x − x 3x − x x (3 x −1) B = − . Đk x > 0. B = − 0,25 x + x +1 x x + x +1 x
B = x ( x − ) 1 − (3 x − )
1 = x − 4 x +1 0,25
B = 1  x − 4 x = 0 0.25
 x = 0 (loại) hoặc x = 16 (thỏa x > 0). Vậy x = 16. 0.25 Câu a)
Do A và B đối xứng qua trục Oy nên tam giác AOB vuông cân tại O. 0,25 2
(1,0) Gọi H trung điểm AB thì các tam giác OHA;OHB vuông cân tại H 0,25 (2,0)
Nên xA = 2; xB = ‒2 và yA = yB = 2 (giả sử A bên phải Oy) 0,25 1
Khi đó thay vào hàm số ta được 2 = 4a => a = 0,25 2 b) 2
x + (m − 2) x − (m − ) 1 (2m − 3) = 0 (1) (1,0)
Lập  = (m − )2 + (m − )( m − ) = ( m − )2 2 4 1 2 3 3 4 . 0,25 3
Phương trình (1) có hai nghiệm phân biệt khi  > 0, tức là m  . 4
Tìm được hai nghiệm là x = m −1; x = 2 − m + 3 0,25 1 2 5 Nếu 2
x = x thì m − = (− m + )2 2 1 2
3  4m −13m +10 = 0  m = 2;m = 0,25 1 2 4 5 Nếu 2
x = x thì − m + = (m − )2 2 3
1  m =  2 và kết luận m{2; ; 2;− 2} 0,25 2 1 4 Câu a) ( 0,25 x − + )2
3 2 + x = 13 (1). Điều kiện: x ≥ 3 3 (1,0) (2,0)
(1)  x − 3 + 4 x − 3 + 4 + x = 13 0,25
 2 x − 3 = 6 − x . Bình phương, thu gọn: x2 ‒ 16x + 48 = 0 0,25
Giải được x = 4 hoặc x = 12. Thử lại và kết luận x = 4. 0,25 b)  1 3 (1,0) + = −2
x − 2 y +1 
ĐK x  2; y  1 − ; đăt 1 1 a = ;b = 0,25 5 2  − = x − 2 y +1 7
 x − 2 y +1
Hệ phương trình trở thành: a + 3b = 2 −  a =1    0,25 5a − 2b = 7 b  = 1 −  1 = 1  x − 2  x − 2 = 1   0,25 1    y +1 = −1 = −1  y +1 Trang 2
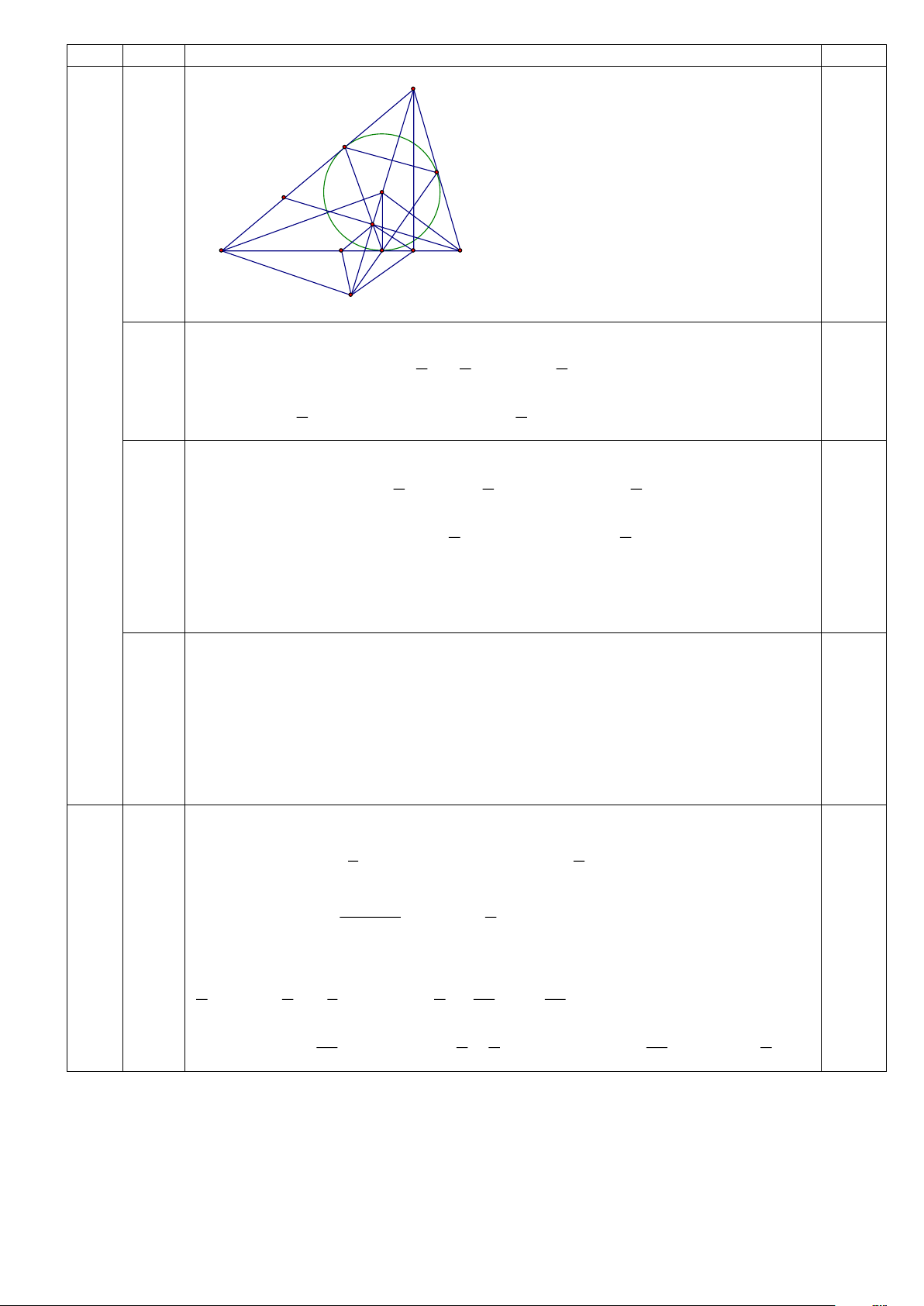
Kết luận; hệ phương tình có nghiêm: (x;y) = (3; ‒2) 0,25 Câu Hình A Câu a): 0.25 4 vẽ Câu b, c): 0.25 (4,0) (0,5) F
Chú ý: Không có hình vẽ không chấm. E I N 0,5 L B C M D H K a)
Do I tâm đường tròn nội tiếp nên AI, BI, CI là các tia phân giác trong các góc 0.25 (1,0) 0 1 1 0 1
Trong BIC có BIC = 180 − B − C = 180 − (B +C) 2 2 2 0.25 0 1 1 BIC = 180 − ( 0 0 180 − a ) (0.25) 0 0 = 90 + a (0,25) 0.5 2 2 b)
Ta có EF ⊥ AI (t/c hai tiếp tuyến) (1) 0.25 (1,0) 1 1 1
Ta có BIK = BAI + ABI = (A+ B) = ( 0 180 -C ) 0 = 90 − C 0.25 2 2 2 1 1 Lại có CI ⊥ DE nên 0 0
EDC = 90 − C hay BDK = 90 − C (đối đỉnh) 0.25 2 2
=> BIK = BDK . Vì I và D cùng phía với BK nên tứ giác BIDK nội tiếp,
Mà DI ⊥ BD nên BI là đường kính, do đó BK ⊥ KI hay BK ⊥ AI (2) 0.25 (1) và (2) => BK // EF c)
Từ BK ⊥ AI , tương tự ta cũng chứng minh được CL ⊥ AI 0.25
(1,0) Gọi N là giao điểm CL với AB, ta được ANC cân ở A (AI vừa ph/g vừa đ/cao) nên L là trung điểm CN 0.25 => ML // AB ( đ trb)  MLK=BAK (đồng vị) 0.25
Tứ giác ABKH nội tiếp nên BHK=BAK (chắn cung BK)
=> MLK=MHK , mà L và H cùng phía MK nên tứ giác KMLH nội tiếp. 0.25 Câu
x ≤ 1; y ≤ 1 nên (x − ) 1 ( y − )
1  0  xy +1  x + y 5 1 3 (0,5)
Mà x + y = 3xy nên (x + y) +1 x + y  x + y  3 2 (x + y)2 4
Và x + y = 3xy  3.  x + y 
(do x  0; y  0) 0.25 4 3
Ta có P = x + y − xy = ( x + y)2 − xy = (x + y)2 − (x + y) = (x + y − )2 2 2 4 6 2 1 −1 4 3 1 1 8 − 3 −  x + y 
  x + y −1 =  P  3 2 3 2 9 4 3 − 1 1 8 − 2 Vây GTLN P = khi ( ;
x y) {(1; );( ;1)} và GTNN P = khi x = y = 0.25 4 2 2 9 3 Trang 3