Điện Học: Lý Thuyết và Bài Tập Tĩnh Điện môn Vật lý đại cương 2 | Học viện Công Nghệ Bưu Chính Viễn Thông

Biên soạn: Phạm Trung Kiên Email: Kien.Pham@campus.lmu.de ĐIỆN HỌC: TĨNH ĐIỆN
(dành cho đối tượng Olympiad)
Sưu tầm và biên soạn bởi Phạm Trung Kiên TÓM TẮT LÝ THUYẾT 1. Định luật Coulomb F=1 r2ˆ q1q2 r.(1) 4πε0 2. Định luật Gauss ,∇ · E=ρ .(2) ε0 ε0 E·dS=Qenc I
Áp dụng để tính điện trường toàn không gian quanh các điện tích đối xứng dạng điểm, dây,
nhẫn, trụ, trụ rỗng, cầu đặc, cầu rỗng. 3. Định luật Stokes E 4. Điện thế ·dl= 0,∇ × E= 0.(3) I E(r) = −∇V(4) 5. Định lý Poisson ∇2V=−ρ (5) 2ε0E2d3r= V ε Z 0
6. Năng lượng tĩnh điện Ues = V 2ρV d3r. (6) Z 1 1 7. Áp suất tĩnh điện p=1 2ε0E2(7) Ngày 15 tháng 3 năm 2025 Trang 1
Biên soạn: Phạm Trung Kiên Email: Kien.Pham@campus.lmu.de BÀI TẬP VẬN DỤNG
Bài tập 1. Áp suất tĩnh điện
(a) Tính lực tác dụng lên mỗi bản của một tụ điện phẳng diện tích Atích điện ±Q.
(b) Tính lực tác dụng lên mỗi nửa bán cầu của một quả cầu rỗng bán kính Rtích điện đều Q.
Bài tập 2. Phân bố điện tích Rutherford
Trong một mẫu mô hình nguyên tử hydro của Rutherford ở trạng thái cơ bản, người ta coi nguyên tử này gồm:
- một proton điện tích +eđược coi là chất điểm đặt tại gốc toạ độ O.
- một đám mây tích điện âm có đối xứng cầu bao quanh proton.
Biết điện thế tại điểm M bất kì (OM =r) có dạng V(r)= a
re−br , với avà blà các hằng số dương.
(a) Hãy xác định điện trường E(r)tại điểm M.
(b) Tính điện tích của đám mây tích điện âm nằm trong mặt cầu tâm O bán kính r.
(c) Tính mật độ điện tích ρ(r)của đám mây điện tích âm theo avà b.
(d) Từ điều kiện trung hoà về điện của nguyên tử hãy tính hằng số atheo evà ε0.
Bài tập 3. Đám mây cầu tích điện đều
Trong không gian vũ trụ, có một đám mây ion dạng đồng chất được tích điện đều có bán kính R
và điện tích tổng cộng Q.
(a) Hãy tìm điện trường, điện thế trong toàn không gian, tính năng lượng tĩnh điện của đám mây.
(b) Dễ nhận thấy từ ý trên, năng lượng tĩnh điện của khối cầu là dương, nó sẽ có xu hướng nở ra
mọi hướng, nhưng trên thực tế các đám mây đều cân bằng. Điều này là do các hạt tích điện
có một suất căng bề mặt σ. Hãy tìm bán kính đám mây R0khi cân bằng.
Bài tập 4. Mô hình phân cực điện thô
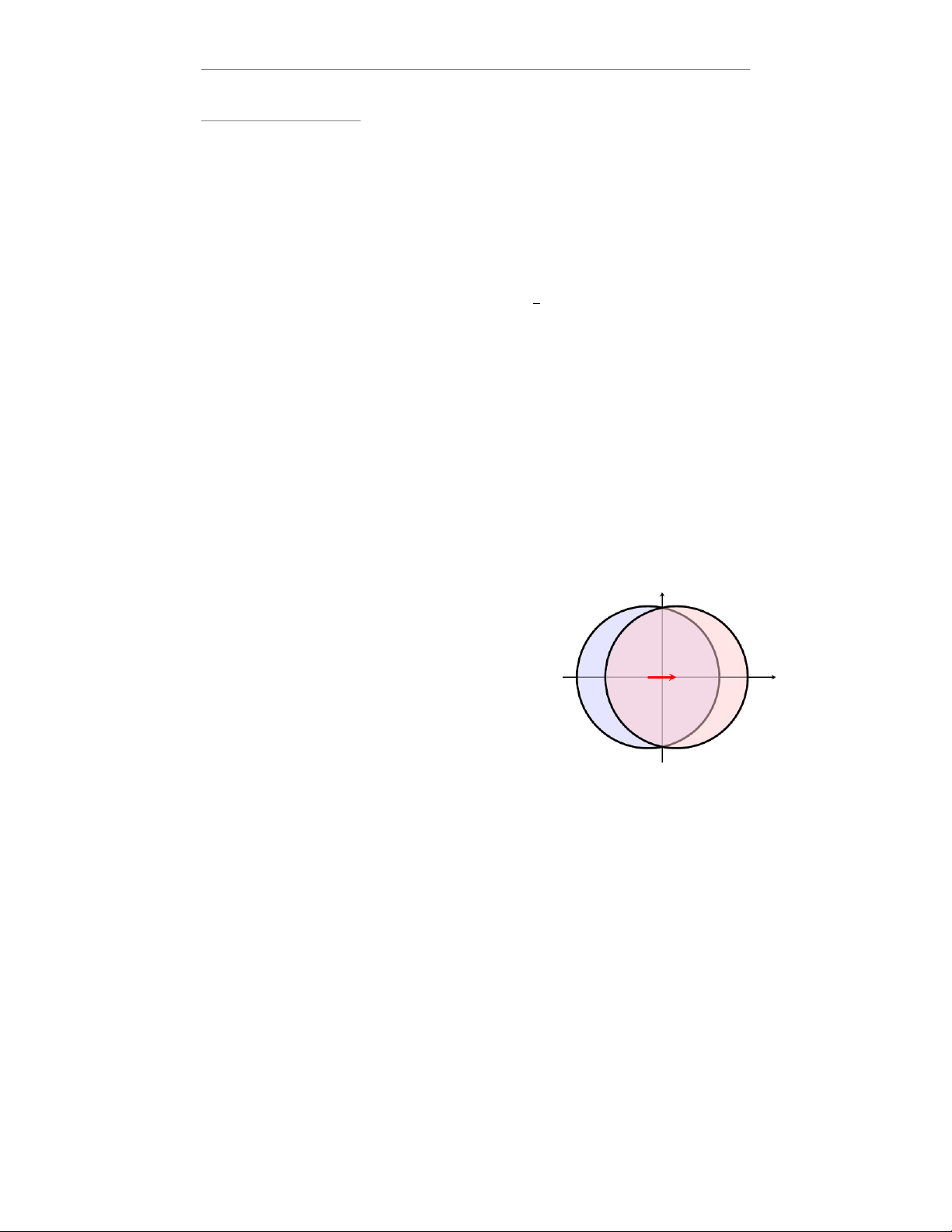
Một đám mây dạng cầu bán kính Rtrung hoà về điện tích phân y
bố đều. Khi bị đặt trong một điện trường, các electron dịch về
phía điện trường còn các proton bị đẩy ra khỏi nguồn điện trường.
Khi đó, do nguyên lý chồng chập, ta coi hệ thành hai đám mây
tích điện +Q(Q > 0) và −Qhình cầu bị tách ra và hai tâm của
đám mây cách nhau một khoảng δ(δ≪R), có thể gọi đại lượng δ
này là độ dài lưỡng cực điện. O−O+ x
(a) Hãy tìm điện trường Ebên trong quả cầu. item Hãy tìm
độ phân cực Pcủa lưỡng cực đám mây và tìm mối liên hệ giữa Evà P.
(b) Hãy tìm phân bố điện mặt σtrên bề mặt quả cầu
Bài tập 5. Tụ điện lệch (HSGSO 2016)
Cho một tụ điện gồm hai bản tụ phẳng hình vuông cạnh ađặt song song cách nhau một đoạn là
d, được nối vào nguồn có hiệu điện thế Ukhông đổi. Quay nhẹ bản dương của tụ quanh một cạnh
của nó đi một góc nhỏ φ. Ngày 15 tháng 3 năm 2025 Trang 2
Biên soạn: Phạm Trung Kiên Email: Kien.Pham@campus.lmu.de
(a) Coi các đường sức trong tụ gần đúng là các cung tròn đồng tâm. Tìm biểu thức của cường độ
điện trường Etại sát mặt bản dương theo khoảng cách đến cạnh cố định của bản.
(b) Tìm biểu thức của điện dung tụ điện.
(c) Tìm công tối thiểu để quay bản tụ.
Bài tập 6. Thấu kính tĩnh điện (HSGSO 2016)
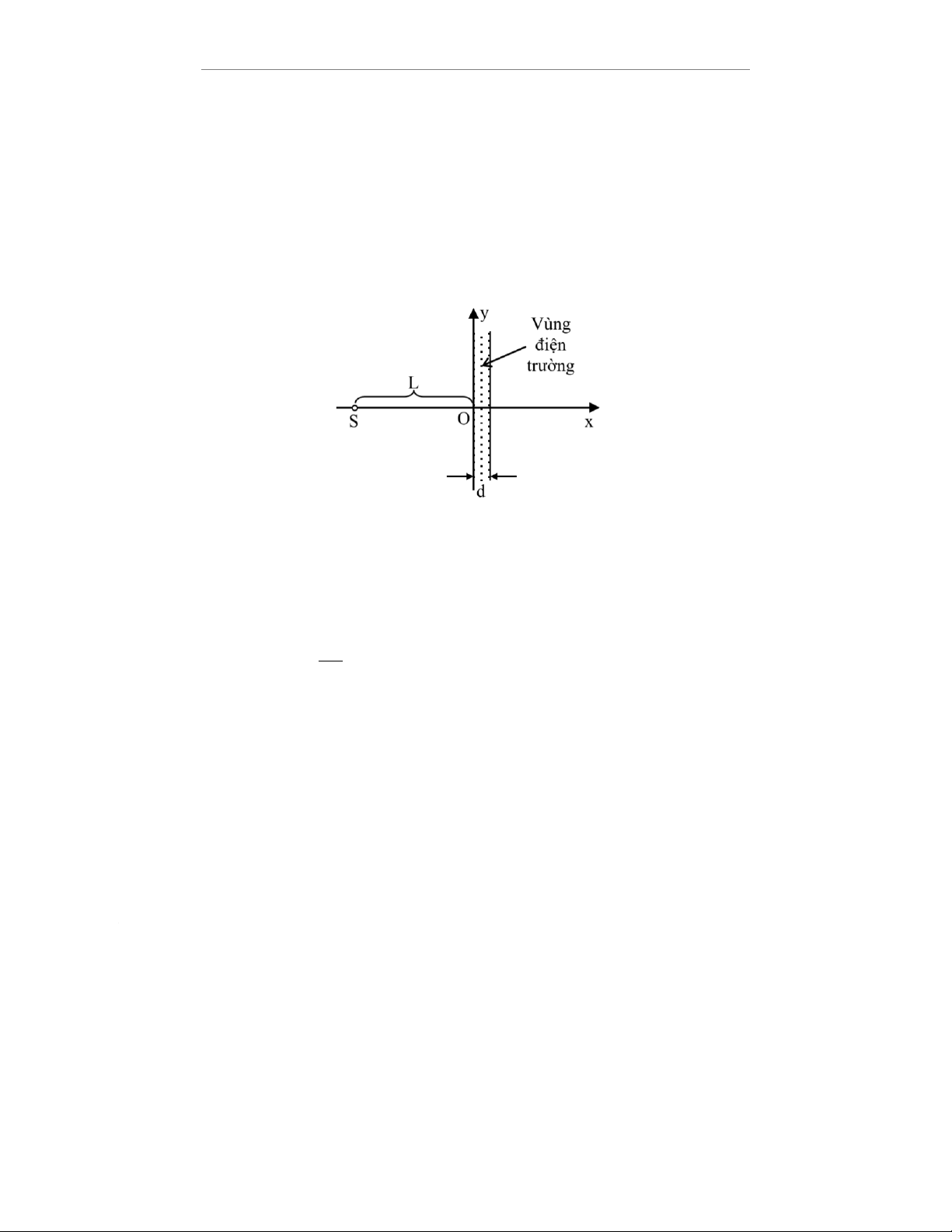
Cho một nguồn Sphát ra các electron có tốc độ bằng nhau và bằng v0. Các electron được cho bay
qua một vùng điện trường hẹp có bề rộng d. Nguồn phát nằm cách biên của vùng một khoảng là
L(L≫d). Chọn hệ quy chiếu như hình vẽ. Khối lượng và điện tích của electron lần lượt là m và
qe=−e. Bỏ qua tương tác giữa các electron và tác dụng của trọng lực. (Luxu ý: Các ý 1 và 2 sau đây là hai bài toán)
1. Điện trường được tạo ra bởi một hệ điện tích phân bố theo một quy luật xác định. Sau khi
các electron bay qua vùng điện trường, chúng chuyển động theo phương song song với trục
Ox. Tìm biểu thức mật độ điện khối của vùng điện trường tại vị trí có tọa độ y.
2. Điện trường được tạo ra nhờ hai lưới kim loại đặt vuông góc với trục Ox, được nối vào hiệu
điện thế Ukhông đổi. Gọi ivà rlần lượt là góc hợp giữa phương của electron đi tới và của
electron rời khỏi vùng từ trường với phương của trục Ox. (a) Tìm tỉ số sini sinr.
(b) Các electron ló ra khỏi điện trường trong lân cận khá gần với trục Ox giống như được
phát ra từ "ảnh" S′của nguồn S. Tìm vị trí của S′.
Bài tập 7. Bẫy electron (HSGSO 2017)
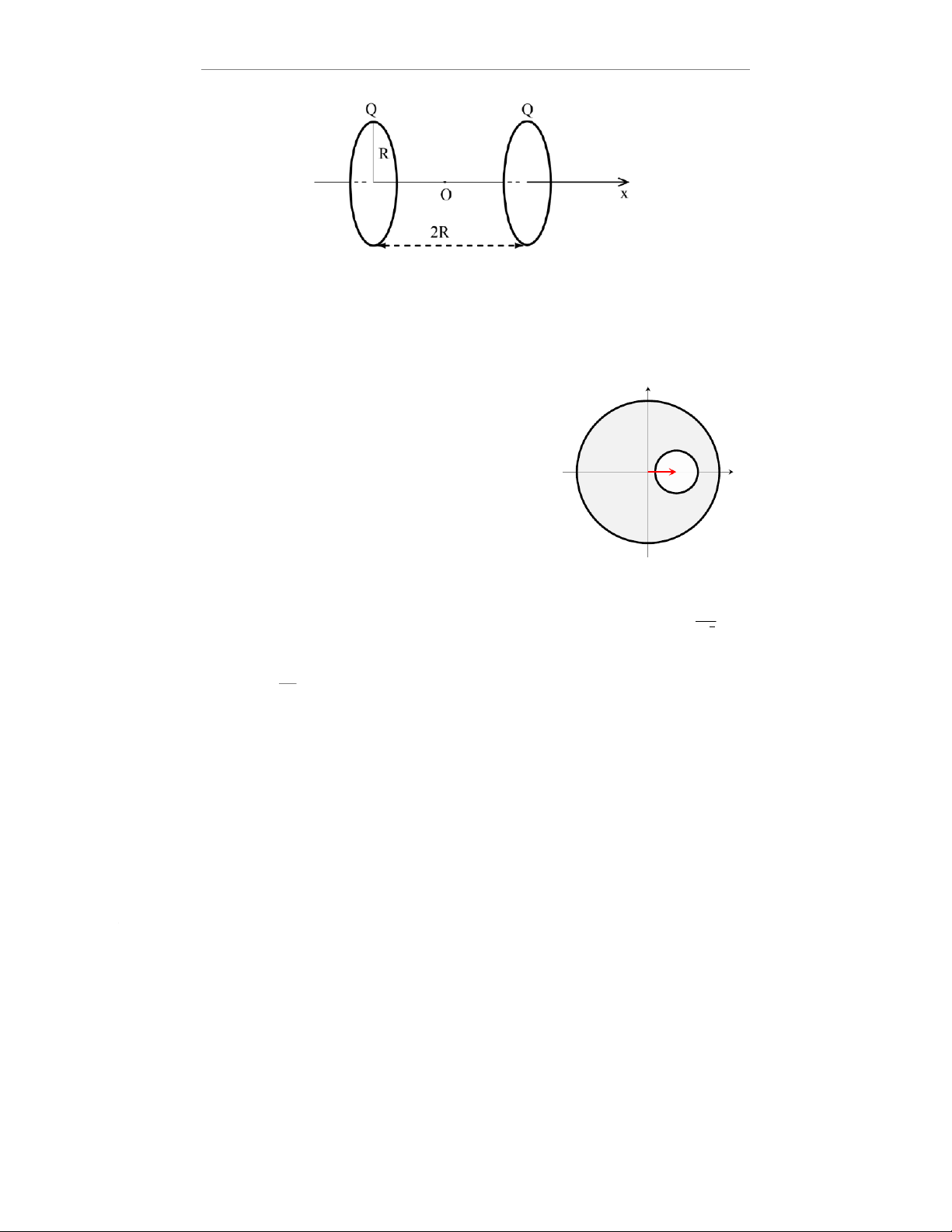
Câu 5. Cho hai vòng kim loại mảnh giống hệt nhau, bán kính R, mỗi vòng có điện tích Q > 0được
phân bố đều trên toàn vòng. Hai vòng được đặt cố định song song với nhau trong chân không,
khoảng cách giữa hai vòng là 2R. Chọn trục tọa độ Ox trùng với trục đối xứng của hai vòng với
gốc tọa độ Ođặt tại điểm cách đều hai vòng (xem hình).
(a) Xác định cường độ điện trường tại điểm bất kì trên trục x. Ngày 15 tháng 3 năm 2025 Trang 3
Biên soạn: Phạm Trung Kiên Email: Kien.Pham@campus.lmu.de
(b) Một điện tích dương q, khối lượng m chuyển động dọc theo trục x từ xa vô cùng lại gần hai
vòng với vận tốc ban đầu v0. Bằng phương pháp đồ thị, hãy cho biết v0phải thỏa mãn điều
kiện gì để điện tích qcó thể đi đến gốc tọa độ.
(c) Liệu có tồn tại vị trí mà ta có thể đặt điện tích qnằm yên ở đó không? Nếu có thì đó là vị trí
cân bằng bền hay không bền?
Bài tập 8. Quả cầu tích điện bị khoét (HSGSO 2020) y
Một khối cầu có bán kính ađược tích điện đều dến mật độ điện khối ρ
ρ. Trong khối cầu người ta khoét một lỗ hình cầu bán kính b
(b < a) sao cho tâm hai vùng đặc và rỗng cách nhau một khoảng d d(dx OaOb
(a) Hãy tìm điện trường ECbên trong vùng khoét. b
(b) Đặt quả cầu vào một điện trường đều E0, hãy tìm lực tác
dụng vào quả cầu và momen lực so với gốc Oa. a
Bài tập 9. Tụ điện phẳng có điện môi biến thiên (HSGSO 2014)
Tụ điện phẳng gồm hai bản tụ phẳng có diện tích S, đặt song song cách nhau một đoạn d, được
nối vào hiệu điện thế Ukhông đổi. Phần không gian giữa hai bản tụ được lấp đầy bởi một chất có
hằng số điện môi biến thiên theo phương vuông góc với mặt bản theo quy luật: ε(x)= ε v 1 1+ ới x x d
là khoảng cách đến bản tích điện dương.
(a) Độ lớn của véctơ cuờng độ điện trường tại một vị trí trong điện môi tuân theo quy luật: E(x)= E0
ε(x). Tìm biểu thức của E0.
(b) Tìm năng lượng của tụ điện.
(c) Tìm mật độ điện tích khối tại vị trí cách bản dương một đoạn x.
Bài tập 10. Tụ điện cầu (HSGSO 2017)
Một tụ điện cầu không khí có bán kính ngoài là R=4 cm còn bán kính trong là rthay đổi được.
Đầu tiên, điều chỉnh để r=1 cm. Khi đó tụ điện này sẽ bị đánh thủng nếu hiệu điện thế đặt vào
hai cực của nó vượt quá 15 kV.
(a) Tính cường độ điện trường đánh thủng không khí. Ngày 15 tháng 3 năm 2025 Trang 4
Biên soạn: Phạm Trung Kiên Email: Kien.Pham@campus.lmu.de
(b) Nối hai cực của tụ với nguồn điện có hiệu điện thế không đổi bằng U=15 kV rồi điều chỉnh
chậm giá trị của rsao cho tụ luôn không bị đánh thủng. Hỏi trong quá trình đó tụ có thể tích
một lượng điện tích cực đại bao nhiêu?
(c) Điều chỉnh rđến giá trị sao cho tụ không bị đánh thủng khi được nối với một nguồn điện có
hiệu điện thế lớn nhất có thể. Tính giá trị của rvà hiệu điện thế cực đại đó.
Bài tập 11. Đám mây vũ tích
Sét là một trong những hiện tượng thiên nhiên kỳ vĩ nhất trên Trái Đất. Rất nhiều nghiên cứu đã
được thực hiện về sét, và trong những năm gần đây, người ta cũng quan sát thấy các hiện tượng
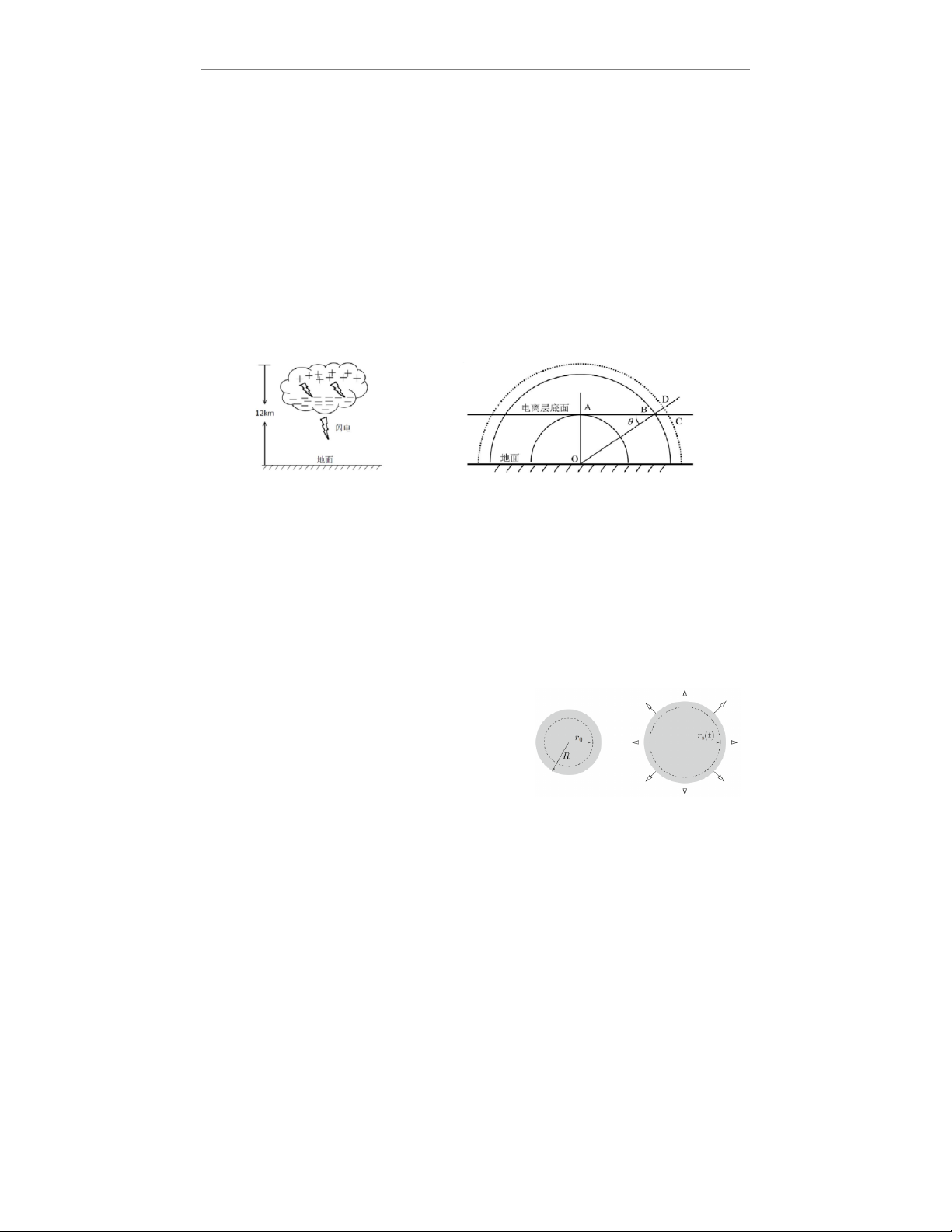
mới như phát sáng chấp nhoáng và vụ nổ tia gamma do sét gây ra. Khi các đám mây sấm sét (cách
mặt đất 6-12km) phóng điện, hầu hết các tia sét xuất hiện trong đám mây và một số ít chạm tới
mặt đất. Do các hạt băng trong đám mây va chạm với nhau nên các tinh thể băng nhỏ tích điện
dương và bay lên đỉnh của đám mây với luồng không khí; các hạt lớn hơn mang điện tích âm và rơi
xuống đáy của đám mây (Xem Hình a). Sét trong đám mây sẽ trung hòa các điện tích âm và dương
trong đám mây, trong khi sét từ đám mây truyền xuống mặt đất sẽ truyền điện tích âm xuống đất.
(a) Sử dụng các khinh khí cầu khí tượng, người ta đã đo được điện trường trong đám mây có thể
coi là đều và có cường độ 0.15MV/m. Bán kính và độ dày đám mây lần lượt là R=2.5km và
d=1km. Tìm hiệu điện thế và điên tích giữa hai mặt đám mây và năng lượng điện trường bên trong nó.
(b) Quá trình va chạm giữa các hạt trong đám mây sẽ càng ngày xảy ra dữ dội, và điện tích giữa
hai mặt của mây sẽ tăng theo cấp số nhân. Khi điên trường tại mỗi mặt đạt đến 1kV/m, sẽ
xảy ra hiện tượng đánh thủng và sét sẽ đánh xuống đất. Cho rằng độ cao mặt tích điện âm
của mây ở độ cao h=6km. Coi mặt đất là một vật dẫn tốt, tìm năng lượng tĩnh điện của
đám mây và điện trường tại mặt đất. (Có thế sử dụng phương pháp ảnh điện).
Bài tập 12. Vụ nổ Coulomb
Trong không gian giữa các vì sao có một đám mây được tạo
bởi Nhạt coi như các điện tích điểm đặt trong chân không,
mỗi hạt có điện tích −q(q > 0), khối lượng m. Ở thời điểm
ban đầu (t=0) các điện tích của đám mây đang đứng yên
và phân bố đều trong một quả cầu bán kính R. Giả thiết
các điện tích không bức xạ năng lượng và bỏ qua hiệu ứng tương đối tính.
1. Do lực đẩy Cu-lông (Coulomb), đám mây bắt đầu dãn nở nhưng vẫn giữ được tính đối xứng cầu.
Giả thiết các hạt chỉ chuyển động theo phương bán kính và không vượt qua nhau. Bỏ qua tác dụng
của tất cả các lực khác. Ngày 15 tháng 3 năm 2025 Trang 5
Biên soạn: Phạm Trung Kiên Email: Kien.Pham@campus.lmu.de
(a) Chứng minh rằng phương trình vi phân mô tả chuyển động của lớp cầu có bán kính từ
r0→r0+dr, với r0+dr < R có dạng md2 d r t2=1 Nrq22r0 R 3.   4πε0
Chứng minh rằng mật độ hạt trong không gian luôn đều trong quá trình đám mây dãn nở.
(b) Xét một điện tích của đám mây mà tại thời điểm t=0 nó đang ở vị trí có bán kính R. Tính
thời gian để điện tích này chuyển động đến vị trí có bán kính 9R.
2. Ở thời điểm t=0, xuất hiện một quả cầu điện môi mang điện tích dương có tâm trùng với tâm
của đám mây, bán kính R0(R0< R). Tại thời điểm nào đó, điện tích của quả cầu phân bố đều với mật độ ρ=3Nq
còn các điện tích âm của đám mây chỉ phân bố trong không gian từ R 4πR 0đến R 3 0
với mật độ được giả thiết chỉ phụ thuộc vào khoảng cách r(tính từ tâm quả cầu điện môi) theo quy luật ρ(r)= A
rα,α > 3và không đổi, Alà một hệ số.
(a) Tìm A theo α,q,N,R0và R.
(b) Tính cường độ điện trường, điện thế ở trong và ngoài đám mây. Cho biết:
xx−adx = x(x−a)+aln(√x+√x−a)+C, với a,Clà hằng số, 0< a < x. Zr p
Bài tập 13. Dao động của hạt trong vòng nhẫn z
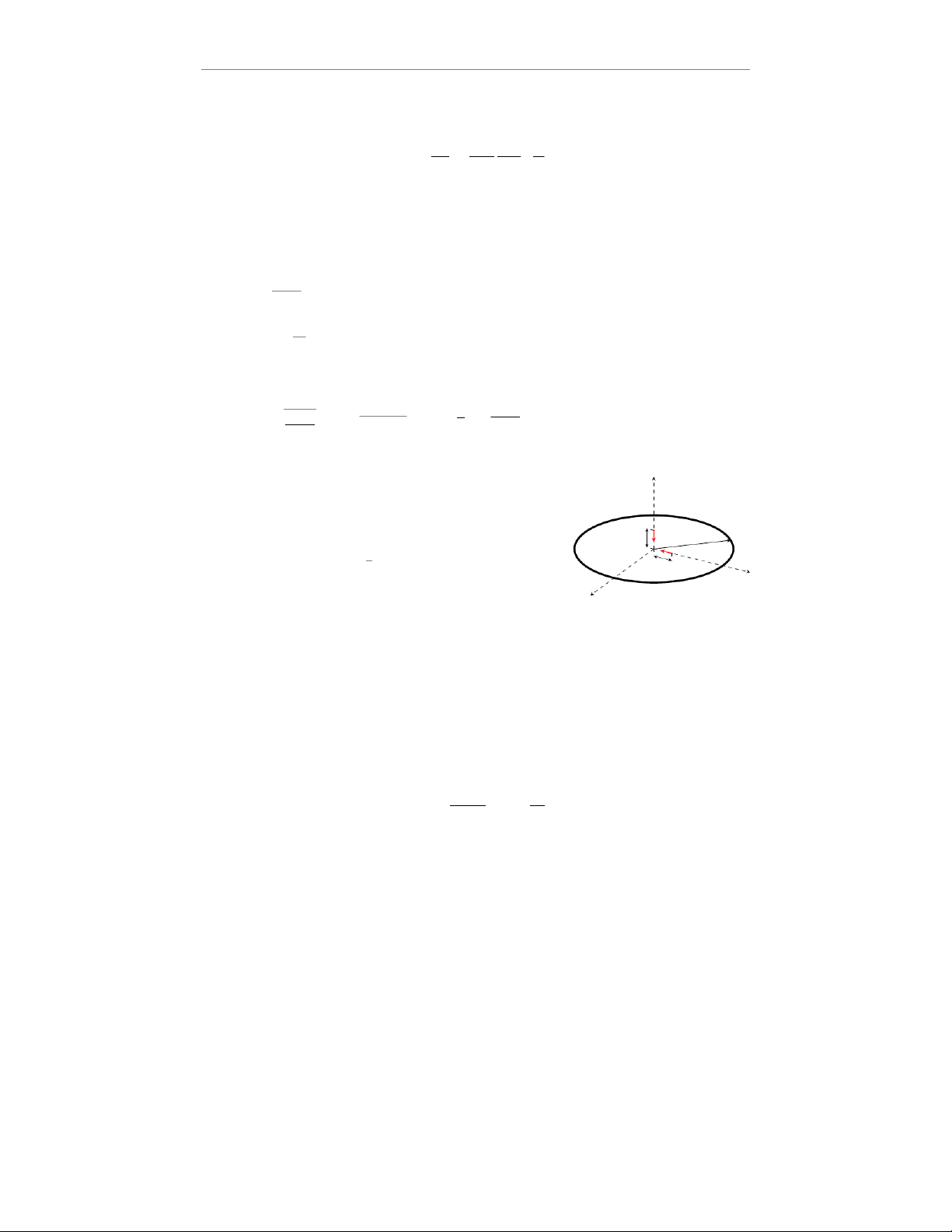
Một vòng nhẫn mảnh có dạng vòng tròn bán kính Rđược tích
điện +Q(Q > 0) đều theo chu vi của vòng, đặt vòng sao cho mặt
phẳng vòng nằm trên mặt phẳng Oxy. Cho biết xấp xỉ Taylor bậc 2 có dạng A z R
(1+x)n≈1+nx +1 2n(n−1)x2,khi |x| ≪ 1. r B y
Ta sẽ đi nghiên cứu chuyển động của hạt tích điện theo hai thành +Q
phần là phương zvà phương bán kính r.x 1. Theo phương z.
(a) Hãy tính điện thế Vztrên trục ztheo độ cao zđối với tâm O.
(b) Tại vị trí z≪R, hãy chứng minh rằng nếu hạt thử là electron thì hạt sẽ dao động quanh gốc
Otheo trục zvà hãy tìm chu kỳ dao động Tzcủa chuyển động. 2. Theo phương r.
(a) Chứng minh rằng điện thế tại điểm nằm trên mặt phẳng xy cách tâm Omột đoạn r≪Rcó dạng V=Q4πε0R 1+αr2R2 .  
Hãy tìm giá trị của hệ số α. Ngày 15 tháng 3 năm 2025 Trang 6
Biên soạn: Phạm Trung Kiên Email: Kien.Pham@campus.lmu.de
(b) Hãy chứng minh rằng nếu hạt thử là proton thì hạt sẽ dao động quanh gốc Otrên mặt phẳng
xy và hãy tìm chu kỳ dao động Trcủa chuyển động.
Hãy tính điện trường tại tâm Ocủa một khối bán cầu bán kính Rđược tích điện Qphân bố đều.
Bài tập 14. Lưỡng cực phẳng
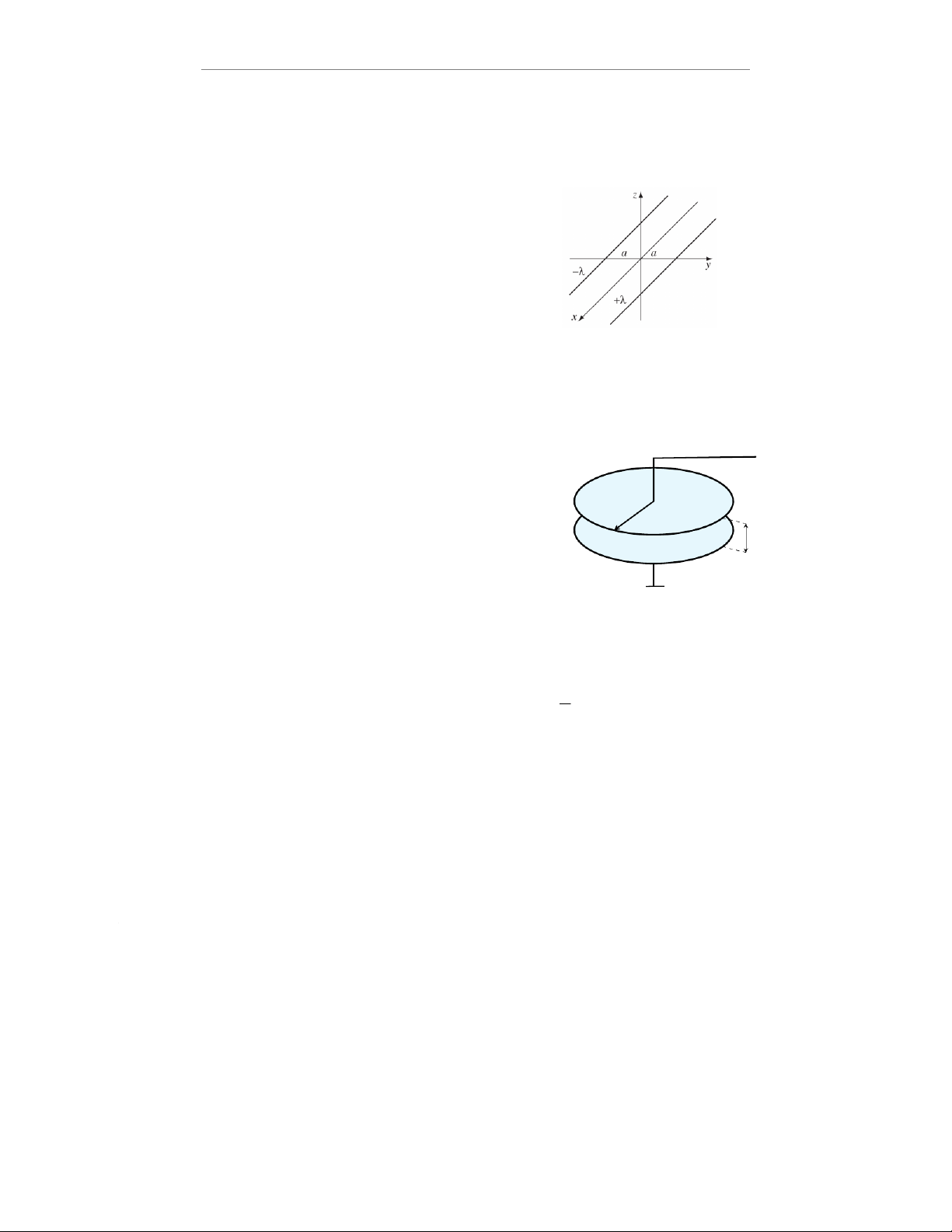
Hai dây dẫn thẳng dài được tích điện đều đến mật độ điện dài
+λvà −λđặt đối xứng với nhau qua trục x, nằm trên mặt phẳng xy và cách nhau 2a.
(a) Hãy tìm điện thế tại một điểm trong không gian (x, y, z).
(b) Chứng minh rằng mặt đẳng thế có dạng hình trụ có trục
là trục x, và tìm bán kính hình trụ có điện thế tại mặt là V0.
Bài tập 15. Chuyển động trong tụ điện
1. Cho một mặt tròn trong chân không, bán kính R, có điện tích phân bố đều với mật độ điện tích
mặt σ. Xuất phát từ công thức điện trường hoặc điện thế gây bởi diện tích điểm, xác định cường
độ điện trường tại điểm Mnằm trên trục đi qua tâm và vuông góc với mặt tròn, cách tâm mặt
một đoạn h. Nhận xét giá trị cường độ điện trường trong trường h≪R.
2. Cho hai bản kim loại tròn, cùng bán kính R, đặt song song
và đồng trục, cách nhau một khoảng d(d≪R) và được giữ cố +V
định. Bản trên được nối với điểm có hiệu điện thế không đổi V
(V > 0) so với đất, bản dưới được nối đất. Không gian giữa hai
bản là chân không. Kim loại dẫn điện tốt, hằng số điện là ε0.
(a) Tính năng lượng điện trường trong không gian giữa hai bản R
và lực tương tác tĩnh điện giữa hai bản theo R,d,ε0và V. d
(b) Một đĩa kim loại tròn rất mỏng, có khối lượng m, bán kính
r(r≪d) được đặt trên mặt và đồng trục đi qua tâm của
bản dưới. Bỏ qua tác dụng của trọng lực, hiệu ứng điện V=0
liên quan đến các mép của bản kim loại và đĩa mỏng, độ
tự cảm và hiệu ứng ảnh điện.
•Giữ đĩa, tìm điện tích qtrên đĩa theo r,d,ε0và V.
•Thả nhẹ đĩa, thấy đĩa liên tục chuyển động lên, xuống giữa hai bản kim loại. Cho rằng đĩa chỉ
chuyển động theo phương thẳng đứng đi qua tâm của các bản kim loại. Va chạm giữa đĩa với
các bạn kim loại là không đàn hồi với hệ số phục hồi k=vs
, trong đó vtvà vstương ứng là vt
tốc độ của đĩa ngay trước và ngay sau mỗi lần va chạm với các bản kim loại. Sau nhiều lần va
chạm, tốc độ vssẽ tiến dần đến một giá trị không đổi v∞là vận tốc giới hạn. Giả thiết rằng
khi va chạm toàn bộ bề mặt của đĩa đồng thời chạm vào bản kim loại và sự trao đổi điện tích
xảy ra một cách tức thời ở mỗi lần va chạm. Tìm vận tốc v∞theo m,r,k,ε0và V.
Bài tập 16. Sự co dãn của màng tế bào
Thành của một neuron thần kinh cấu tạo từ một màng đàn hồi, co dãn giống như một lò xo. Độ
cứng hiệu dụng của lò xo là kvà độ dày khi cân bằng là d0. Giả thiết màng có diện tích Arất lớn Ngày 15 tháng 3 năm 2025 Trang 7
Biên soạn: Phạm Trung Kiên Email: Kien.Pham@campus.lmu.de
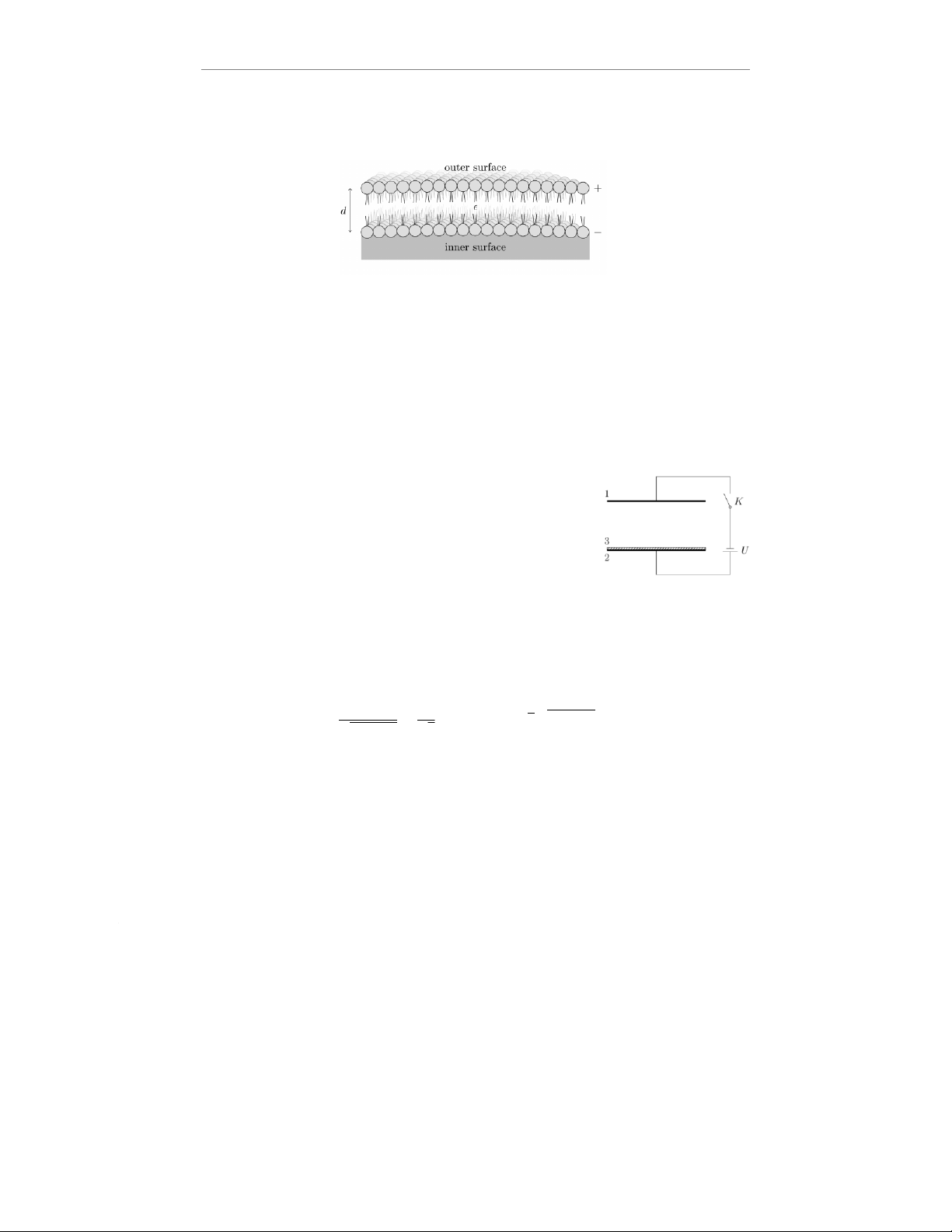
và có thể bỏ qua độ cong của nó. Neuron có thể "bơm ion" đẩy các ion di chuyển qua màng. Kết
quả là tế bào trở thành tích điện, các ion dương và âm phân bố đều trên mặt trong và mặt ngoài
của màng. Hằng số điện môi của màng là ε.
(a) Giả thiết rằng sau khi bơm ion thực hiện một công, điện tích trên các mặt trong và ngoài là
+Qvà −Q. Tìm độ dày dcủa màng.
(b) Thiết lập biểu thức cho hiệu điện thế Vgiữa mặt trong và mặt ngoài của màng theo Qvà các thông số đã cho.
(c) Giả thiết bơm ion đầu tiên được bật lên từ trạng thái chưa tích điện, và màng được tích điện
rất chậm (gần cân bằng). Bơm chỉ ngắt đi khi điện áp trên màng vượt quá một giá trị cụ thể
Vth. Tìm độ lớn độ cứng kcủa lò xo để bơm ion ngắt trước khi màng bị sập xuống.
Bài tập 17. Chuyển động trong tụ điện (HSGSO 2018, CPhO)
Hai bản tụ 1 và 2 của một tụ điện phẳng có tiết diện S, được giữ nằm
ngang ở cách nhau một khoảng d, và được nối vào nguồn điện một chiều
Ukhông đổi. Một bản dẫn điện thứ 3, ban đầu chưa tích điện, có khối
lượng mvà cùng kích thước với hai bản 1 và 2. Bản thứ 3 được đặt lên
trên bản thứ 2 sao cho chúng có tiếp xúc điện. Toàn bộ hệ được đặt
trong chân không có độ điện thẩm ε0. Khi khoá K đóng, bản 3 lần lượt
va chạm với bản 1 và 2 và cứ thế lặp đi lặp lại. Coi rằng điện trường 2 bản tụ là đều,
điện trở dân dẫn và tụ điện là nhỏ, khi bản 3 tiếp xúc với 2 bản còn lại, các điện tích tự do được
thiết lập trạng thái cân bằng ngay tức thì, coi các va chạm là mềm, gia tốc rơi tự do là g.
(a) Tìm giá trị nhỏ nhất của Uđể bản 3 có thể chuyển động như mô tả.
(b) Tìm chu kì chuyển động tuần hoàn của bản 3.
Cho biết giá trị của tích phân sau:
dx√ax2+bx =1 √aln(2ax +b+2√a ax2+bx)+C. Z p
Bài tập 18. Chuyển động tĩnh điện (HSGSO 2020)
1. Cho vòng điện môi cố định có bán kính R, tích điện đều với tổng điện tích +Qvà một điện tích
điểm có khối lượng mvà điện tích +q. Điện tích điểm được đặt trên trục đối xứng của vòng điện
môi, tại vị trí nhìn vòng với góc 2α(Hình 5a).
(a) Tìm lực điện tác dụng lên điện tích điểm q. Tìm αđể lực điện nhận giá trị cực đại. Ngày 15 tháng 3 năm 2025 Trang 8
Biên soạn: Phạm Trung Kiên Email: Kien.Pham@campus.lmu.de
(b) Thả điện tích từ vị trí αtính được ở câu (a). Tìm tốc độ của nó khi ra đủ xa vòng.
2. Cho điện tích điểm có khối lượng mvà điện tích qđặt tại đỉnh một hình nón có chiều dài đường
sinh là Lvà góc ở đỉnh là 2α. Người ta tích điện đều cho phần mặt nón dài L/2với mật độ điện mặt σ(Hình 5b)
(a) Tìm lực điện tác dụng lên điện tích điểm q. Với cùng giá trị Lvà σ, lực điện nhận giá trị cực
đại với αbằng bao nhiêu?
(b) Thả cho điện tích chuyển động. Tìm tốc độ của nó khi ra xa vô cùng. (Góc αlấy theo kết quả của câu trên) Ngày 15 tháng 3 năm 2025 Trang 9