Điện Trường Tĩnh: Định Luật Coulomb và Định Lý Gauss môn Vật lý đại cương 2 | Học viện Công Nghệ Bưu Chính Viễn Thông

TRƯỜNG TĨNH ĐIỆN 1. Mở đầu 2. Định luật Coulomb 3. Điện trường 4. Định lý Gauss 5. Điện thế
6. Mối liên hệ giữa cường độ điện trường và điện thế 1. Mở đầu
Điện tích: Thuộc tính tự nhiên của những hạt cơ bản có kích thước rất nhỏ
(không thể nhìn thấy bằng mắt thường) tạo lên liên kết về điện trong nguyên tử. Proron (p):
Nguyên tử: Phần tử cơ sở cấu tạo vật chất điện tích (+)
- Trạng thái bình thường: trung hòa điện số e và p bằng nhau, Neutron: Không điện tích
- p gắn cố định trong hạt nhân nguyên tử,
e có thể dễ dàng di chuyển dễ tạo ra sự Electron (e) - điện tử:
mất cân bằng điện tích giữa 2 vật trung điện tích (-)
hòa điện khi được cho tiếp xúc với nhau tạo ra i-ôn
Điện tích điểm: Điện tích có kích thước không đáng kể so với khoảng cách
giữa điện tích và 1 điểm trong không gian nằm trong vùng ảnh hưởng của nó. 1. Mở đầu
Điện tích nguyên tố:điện tích của một e (hay p) có giá trị là là 1,6 . 10-19 C,
được qui ước làm giá trị một đơn vi điện tích. Hạt cơ bản Khối lượng Điện tích Electron 9,11.10-31 kg -1,60.10-19 C (-e) Proton 1,672.10-27 kg +1,60.10-19 C (+p) Neutron 1,674.10-27 kg 0
Điện tích của vật thể tích điện: Đại lượng vô hướng được xác định bằng một
số nguyên (kết quả sự chênh lệch số các proton và electron) lần điện tích
nguyên tố trong vật thể, tức là Q=e.(Np-Ne) = n.e
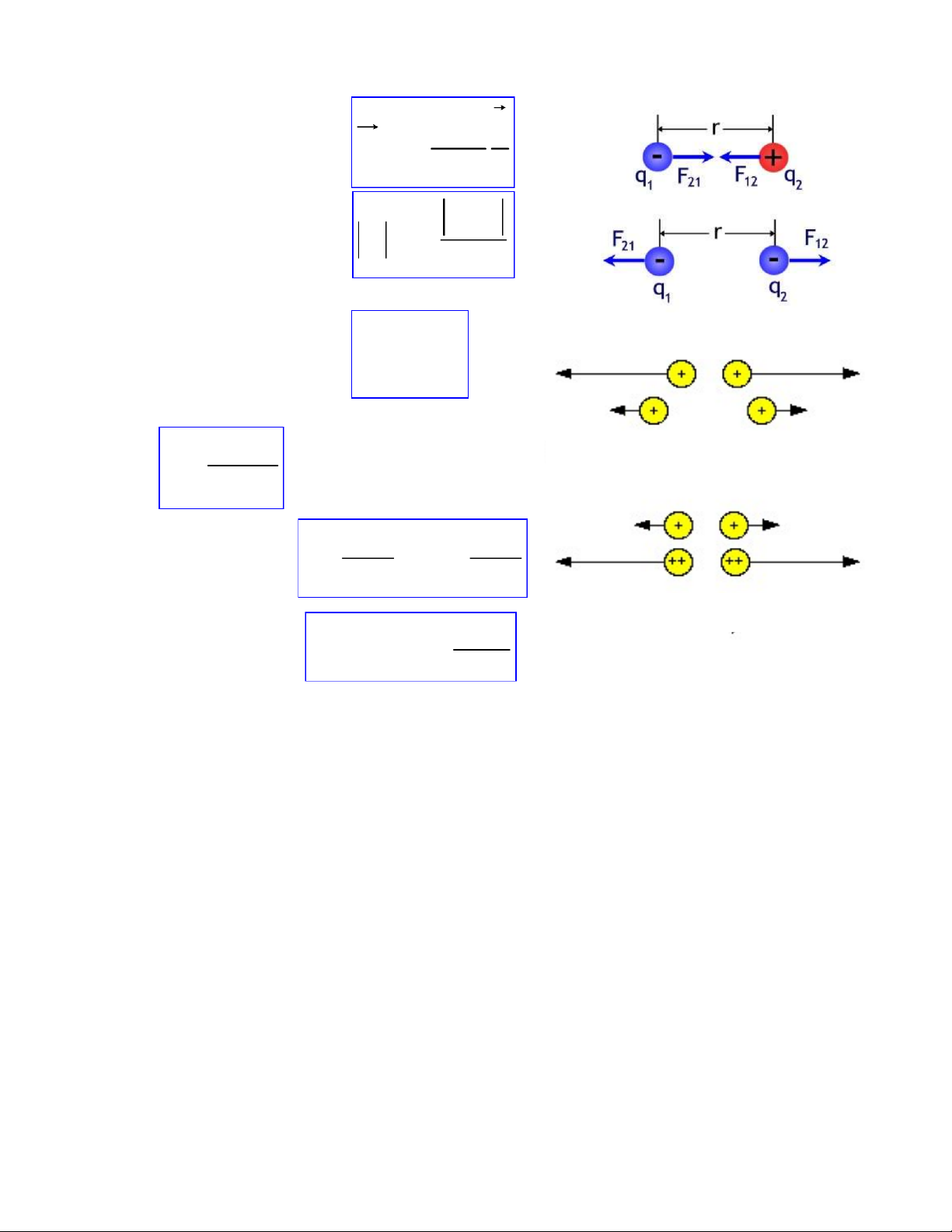
Phân loại: điện tích dương (+) và điện tích âm (-) + + Cùng dấu: đẩy nhau Khác dấu: hút nhau Truyền điện tĩnh:
Bảo toàn điện tích: Điện tích không tự sinh ra hay mất đi mà chỉ dịch
chuyển bên trong một vật
hoặc từ vật này sang vật Cảm ứng Dẫn điện khác Ma sát (tiếp xúc) (điện hưởng)
Phân loại vật liệu theo khả năng truyền điện của điện tích:
- Vật liệu dẫn điện: Điện tích có thể chuyển động tự do trong toàn bộ thể tích vật (kim loại)
- Vật liệu cách điện – điện môi: Điện tích định xứ cố định tại những miền
nào đó, và không thể di chuyển tự do trong vật liệu (cao su, chất dẻo, gỗ, giấy, không khí khô …)
- Vật liệu bán dẫn: Điện tích cũng định xứ cố định tại những miền nào đó,
nhưng có thể di chuyển tự do trong vật liệu dưới tác động của nhiệt độ, ánh
sáng hoặc điện trường ngoài (silicon, germanium…).
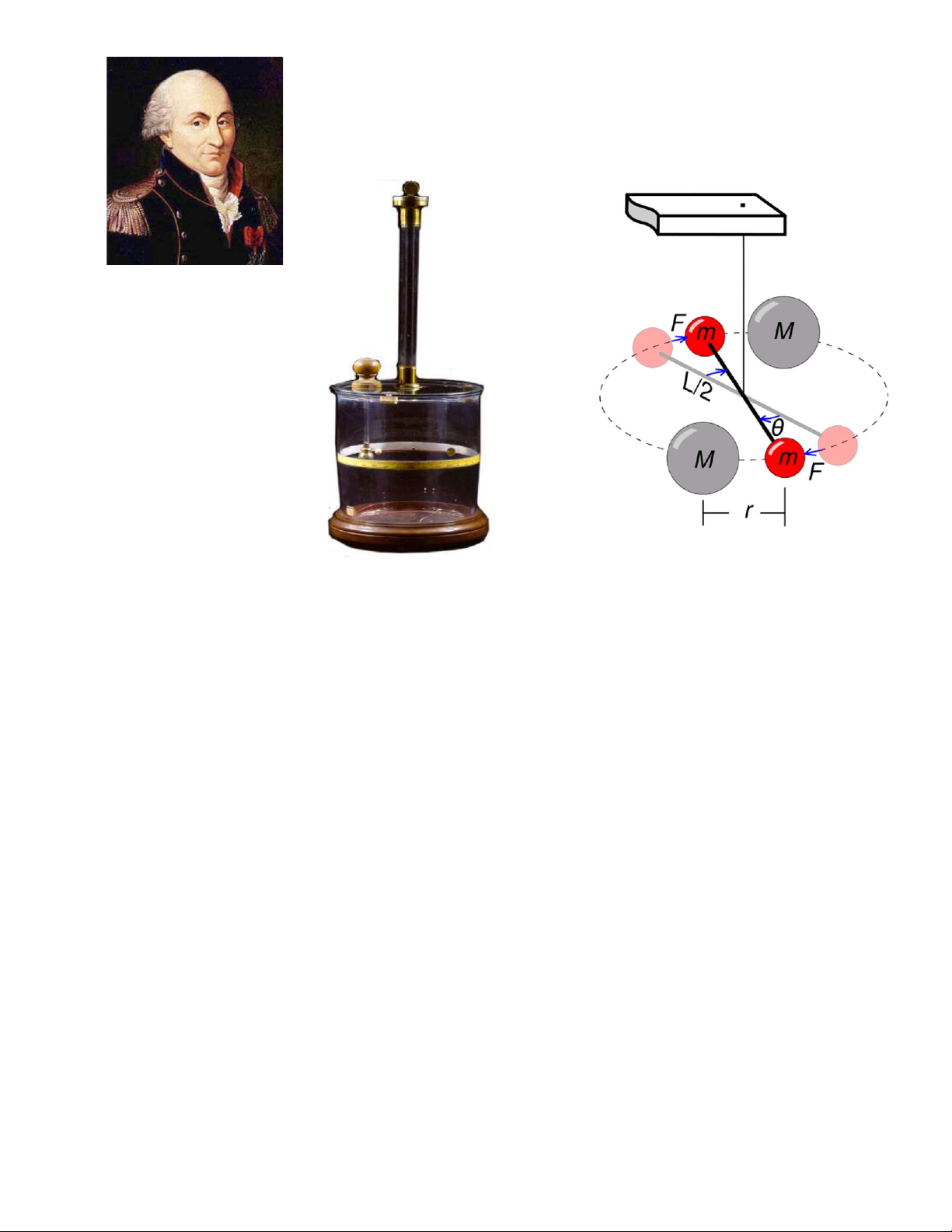
(Định luật về tương tác tĩnh điện) Dây xoắn  Charles-Augustin de Coulomb Cân xoắn Coulomb
Nguyên lý xác định tương tác tĩnh
điện bằng cân xoắn Coulomb 2. Định luật Coulomb Lực tương tác giữa q q r F 1 2 2  k 2 điện tích điểm: r r q q 1 2 Độ lớn: F k 2 r
Tương tác tổng cộng của   
hệ điện tích lên một điện F  n Fi tích điểm thứ i: i1 Hệ số: 1 k 
Gấp đôi khoảng cách, lực giảm 1/4 40 2 1 Nm 9 Trong chân khô  ng k 91 . 0 2 4 C 0
Gấp đôi điện tích, lực tăng 4 lần 2  C 12   8 , 8 . 5 10 0 2 N.m 3. Điện trường
“Trường”:Không gian mà một đại lượng vật lý được xác định tại mỗi điểm
trong đó. Đại lượng vector  trường vector; đại lượng vô hướng trường vô hướng.
Điện trường:khoảng không gian bao quanh các điện tích, thông qua đó tương
tác (lực) tĩnh điện được xác định  điện trường là trường vector.
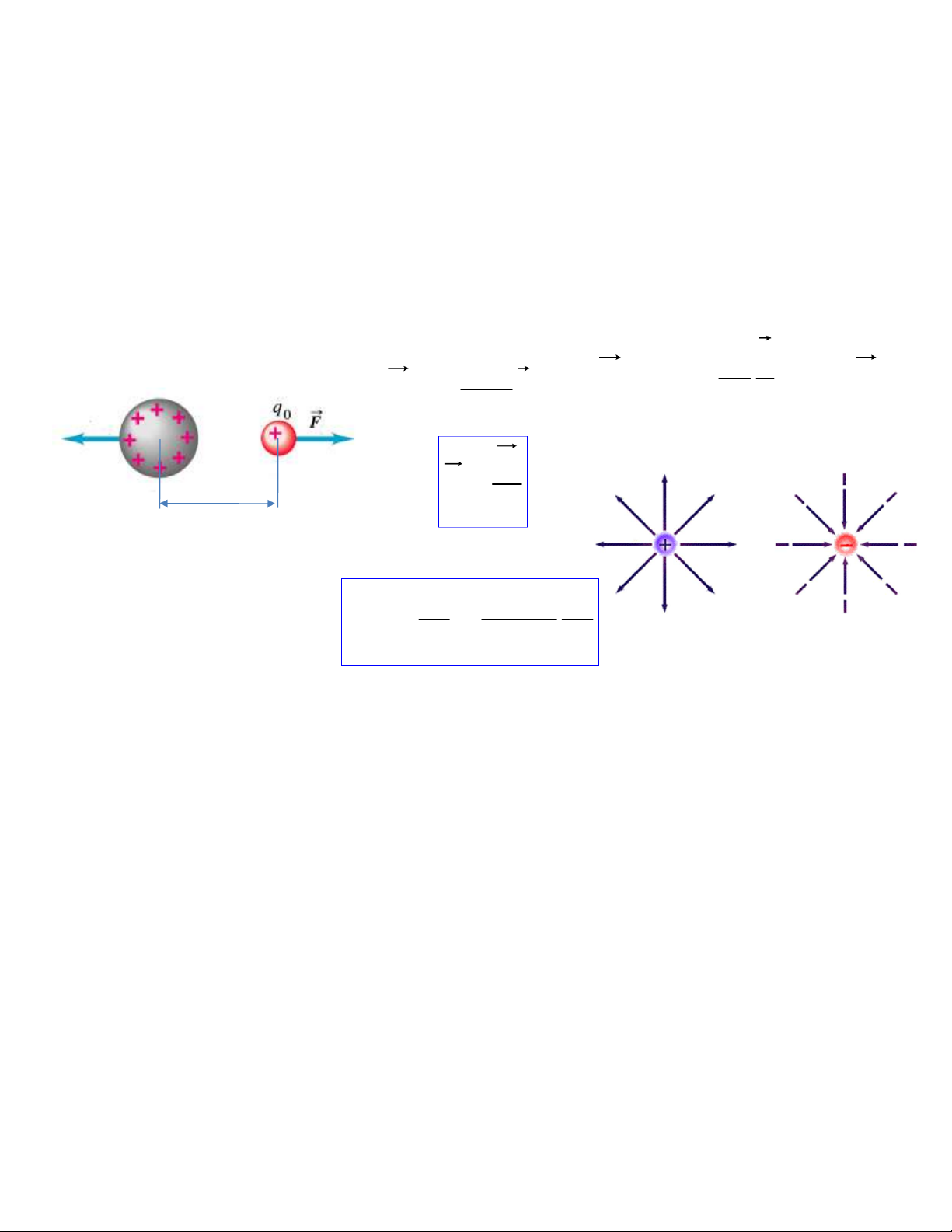
Vector cường độ điện trường:   Q Qq Q r Điện tích thử F 0 F .  q0k  q E 3  k hay r 2 0   r r r    F r E q0
Độ lớn điện trường gây bởi Q tại q0: Q 1 Q E  k  2 r 24  r 0 Đơn vị: N/C hoặc V/m 3. Điện trường
Nguyên lý chồng chập điện trường:Vector cường độ điện trường gây bởi một
hệ điện tích tại bất kỳ điểm nào trong trường là tổng các vector cường độ điện
trường gây bởi từng điện tích tại điểm đó.
Điện trường chồng chập của 2 điện tích điểm (tạ         1 q r q r  1 1 2 2 E E E  2 2  1 4 2  r r r r 0  1 1 2 2  q1q2
Điện trường chồng chập của n điện tích điểm
(tại vị trí của điện tích điểm qi):       n  n      1 q r i i E E E ... E E     1 4 2 n r i 12  1 r i 0 ii i 3. Điện trường 0 Lưỡng cực điện  d
Hệ 2 điện tích điểm trái dấu có độ lớn bằng nhau -qq 
cách nhau một khoảng d (rất nhỏ, khó xác định) p p q  d  E2
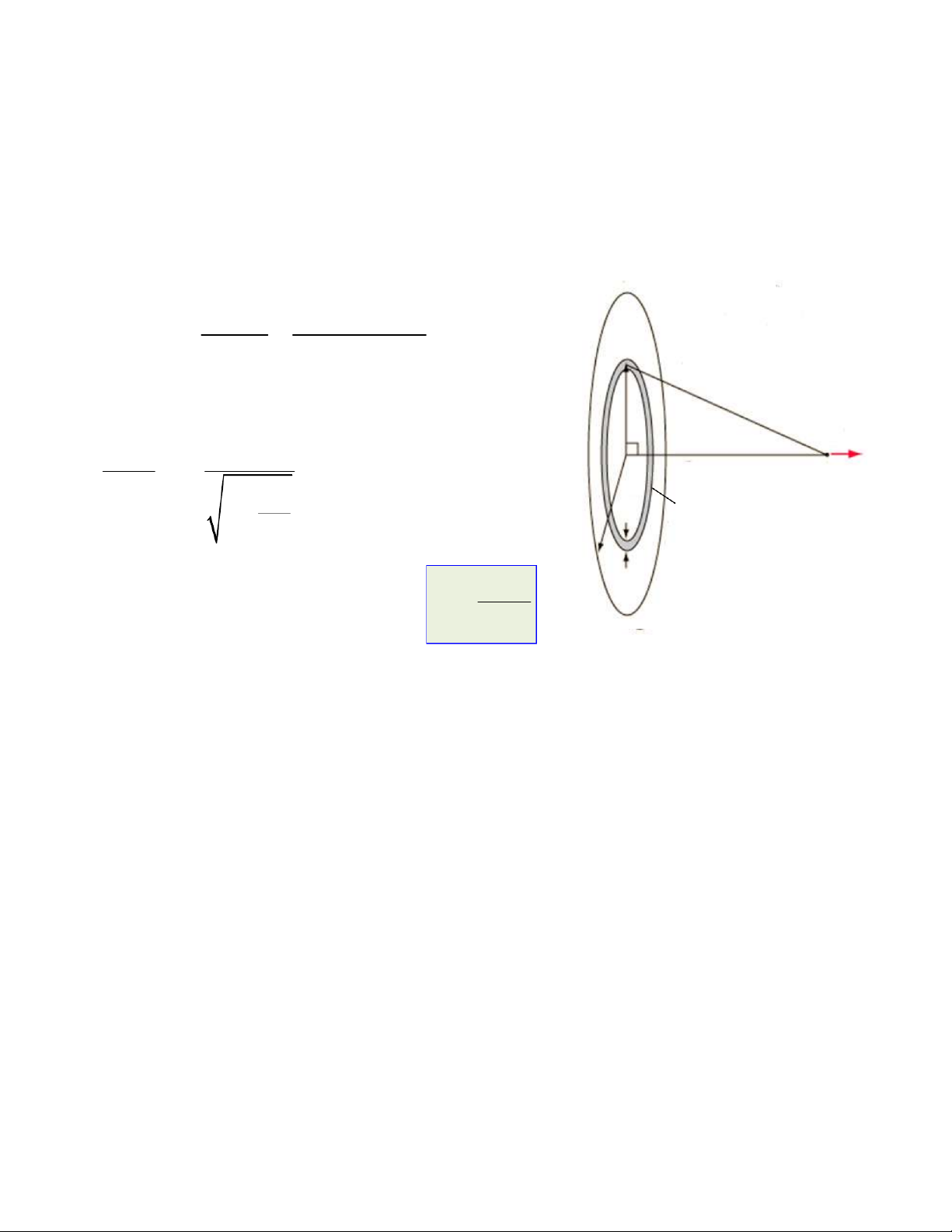
Điện trường gây bởi lưỡng cực điện  
- Tại điểm nằm trên đường trung trực (r>> d) E  M     1 q E C E ó: v E ớ  i: 1 1 E  2 E  E  2 1 4 2  r 0 hay: E=E r r r2 1.cos+E2.cos= 2E1.cos 1 1 p   1 p E 3 hay: E   0 3 4 r 4 r  0 0 -qq d
- Tại điểm nằm trên trục lưỡng cực (r>> d) r    0 1 2 p E  E  3 4 r -qq 0 d N 3. Điện trường
Điện trường gây bởi các vật có phân bố điện tích đều
Điện tích Qcủa vật do các yếu tố điện tích dQ tạo thành điện trường do dQ
gây ra tại 1 điểm cách dQ 1 khoảng r: 1 dQ dE    2 4 r 0 1 dQ
Điện trường do tất cả các dQ phân bố đều trên vật gây ra: E d  E   2 4 r 0
Dây dẫn thẳng tích điện (độ dài 2l, điện tích Q>0, mật độ điện tích dài): Q  dQ  dy dy l 2 l
Điện trường tại P gây bởi dQ: 1 dQ dE   2 dE d  E 4 r x dE y 0 1 dQ x E   dE dE .cos .     x  2 4 r r thanh thanh thanh 0  l x dy 2 l x dy E     4    l x  3/2 3/2 2 2 2 2 4 y x y 0 00   x << l  E  -l 20x l  Ex x  l Q 2   1/2 2 2 x >> l 2E   0 4x 0 3. Điện trường
Điện trường gây bởi các vật có phân bố điện tích đều
Vòng dây tròn tích điện (bán kính a, mật độ điện tích dài , điện tích Q): dQ  ds r x 1 dQ dE  2 40 r 2 1 1  R dQ  x Qx E d  E  cos ds    x  2 3 3 4 r 4 4 r r vòng tròn vòng tròn 0 0 0 0 1 Qx
x =0 (tại tâm vòng tròn): E  0 Ex a   4   3/2 2 2 1 Q 0 x >> a: E  2 4 r 0 3. Điện trường
Điện trường gây bởi các vật có phân bố điện tích đều
Mặt đĩa tròn tích điện (bán kính R, điện tích Q, mật độ điện tích):
Đĩa được chia thành các hình vành khăn có diện tích dS, độ rộng dR’ :
Điện tích dQ của vành khăn:dQ   d  S 2R ' 'dR 2 R x R ' 'dR E d  E x R   4 tròn   3/2 2 '2 00 r   R’ dE    1 E   1 x P 2 21   0 R    R ds 2   x dR’ 
Nếu R  (mặt phẳng vô hạn)  E  20 3. Điện trường
Đường sức điện trường
- Đường cong hình học mô tả điện
trường mà tiếp tuyến tại mỗi điểm của nó
trùng với phương của vector cường độ
điện trường tại điểm đó.
- Chiều đường sức điện trường là chiều
vector cường độ điện trường.
-Điện phổ: tập hợp các đường sức điện trường 4. Định lý Gauss (Karl-Friederich Gauss)
Vector cảm ứng điện (điện cảm)
Vector cường độ điện trường:
Vector cảm ứng điện:  1 q r   1 q r E2 E  D E     D  02 4 r r 0 4 r r
đường sức điện trường gián đoạn
đường sức điện cảm không gián đoạn
khi qua mặt phân cách 2 môi trường
khi qua mặt phân cách 2 môi trường 4. Định lý Gauss Điện thông D, E
Định nghĩa: Thông lượng vector điện cảm (điện
trường) gửi qua một thiết diện có trị số tỉ lệ với S0
số đường sức cắt vuông góc thiết diện đó. e=D.S0
Tiết diện (S)tạo với S0góc  S0=S.cos   n   D e=D.S0=D.S.cos  =DnS (S0)(S) 
Dnlà hình chiếu của D lên pháp tuyến n
Điện trường bất kỳ: xét phần tử diện tích dS n   D de=D.S0=D.dS.cos    d  e. D dS dS  
Điện thông toàn phần gửi qua mặt S:   D. dS e S   (S)
Điện thông toàn phần gửi qua mặt S kín:  D dS e .  S 4. Định lý Gauss dn  D dS
Điện thông xuất phát từ điện tích điểm q M r O Trong mặt cầu (kín) S D. dS D dS D dS D. r  q e 4 S S S
Mặt Gauss quanh điện tích dương: Trong mặt kín S bất kỳ Điện thông dương  Dn D  dn dS cos D dn Góc khối: dr  2 dS   M dS M   . D cdoSs D dS  e   d S S O d dS cos 2 2    Dr d  D r .4 q e S O 4. Định lý Gauss
Điện thông xuất phát từ điện tích điểm q
Ngoài mặt kín S bất kỳ: e=0
Định lý Gauss cho phân bố điện tích gián đoạn:
Thông lượng điện cảm (điện trường) gửi qua một mặt kín bất
kỳ bằng tổng đại số các điện tích nằm trong mặt kín đó  .   n   D dS   q e i S i 1 
Định lý Gauss cho phân bố điện tích liên tục d 1 n q i. dV  Khi đó:    dS i D1 D d  S.  edV dS       S V D3 .vì: D dS. divD dV dn3 dS     divD   S V  D Dy D  với: divD x z dn2    D2 (Phương trình Poisson) x y  z  4. Định lý Gauss
Ứng dụng định lý Gauss xác định cường độ điện trường
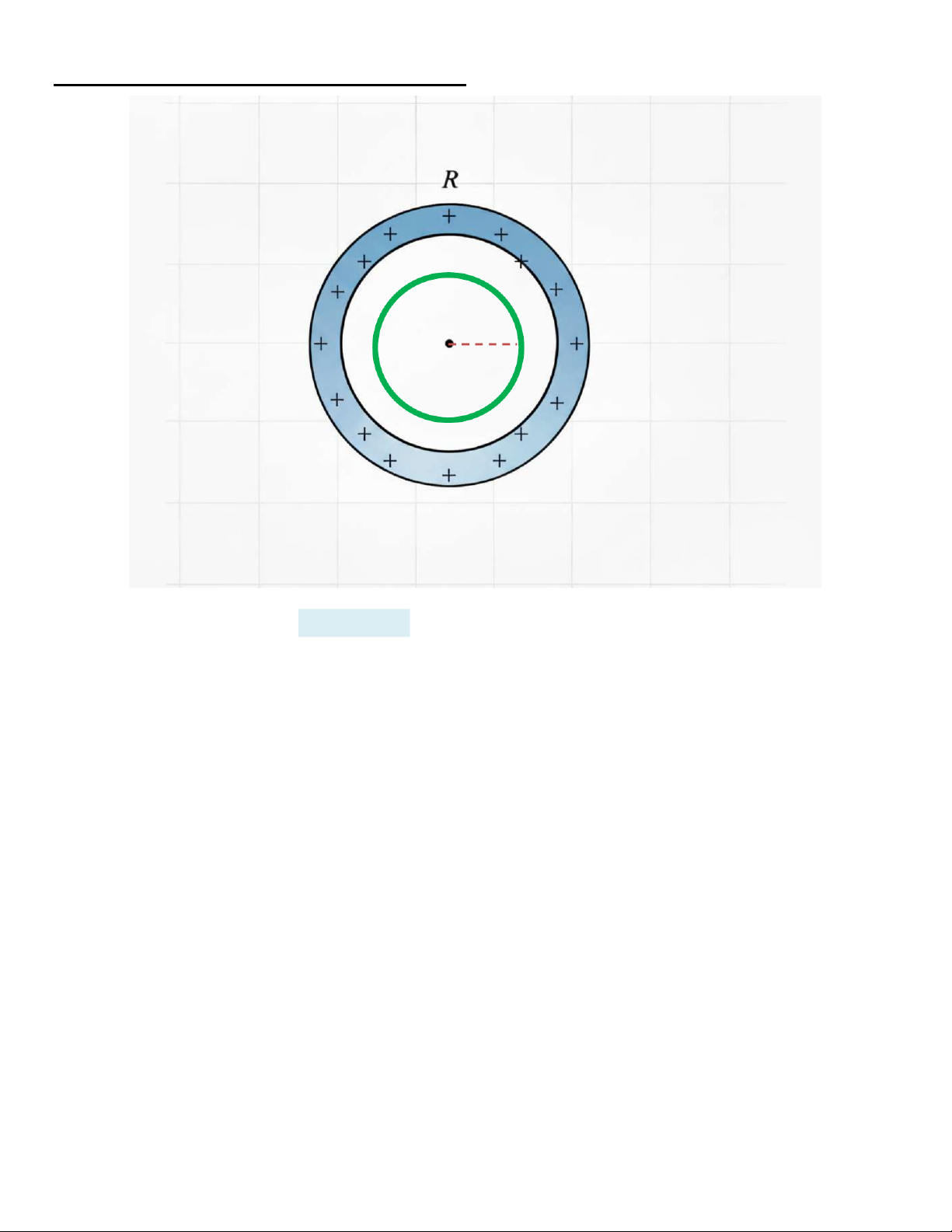
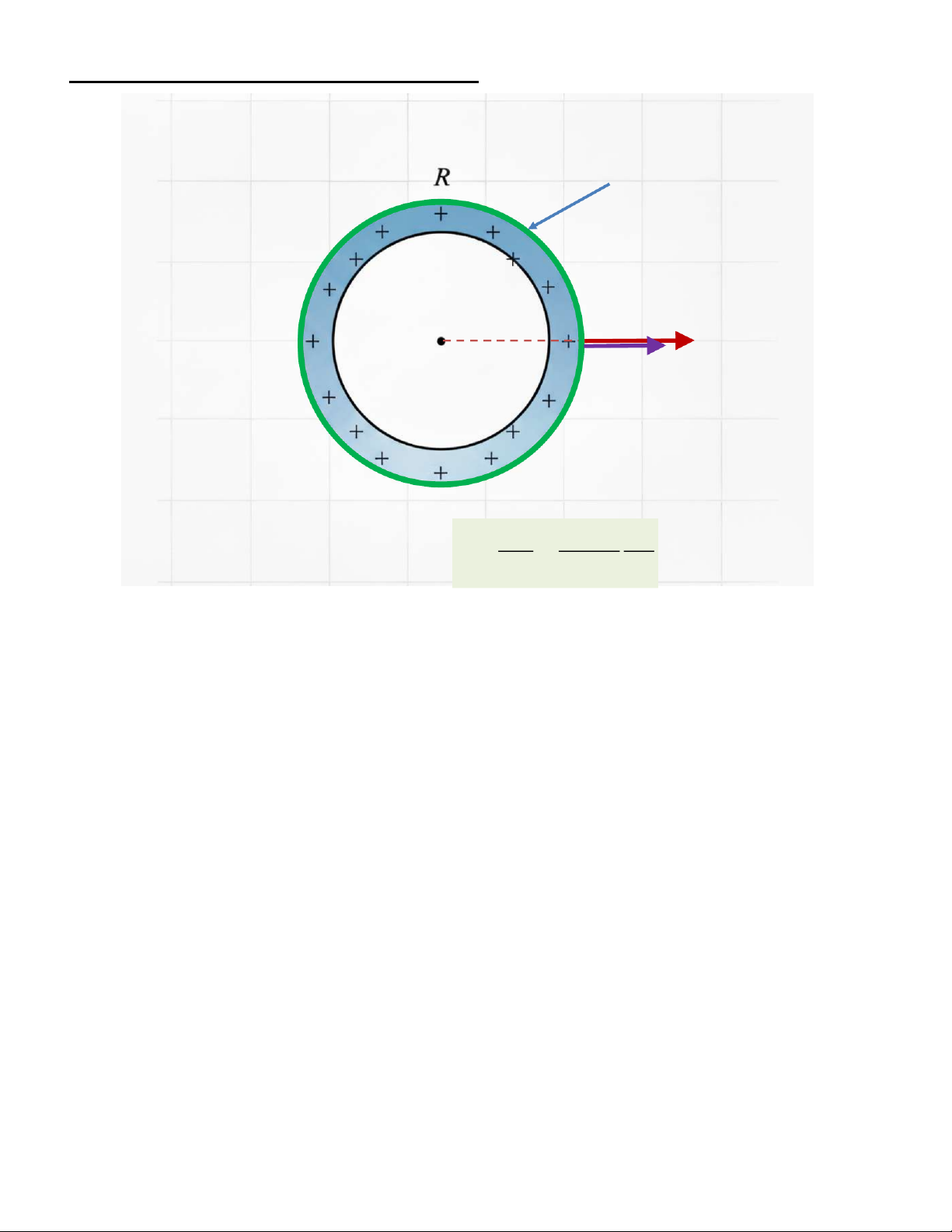
1. Mặt cầu (bán kính R) tích điện đều (q > 0) trên bề mặt
a. Trường hợp r>R - có mặt Gauss r: Mặt Gauss  dq d 1D 2  n R   O M d D D dq  1 d 2D   2 q   D. .4
dS  D dS D dS D  r  q e     D  D 1 q 2 ;    2 4r E   S S S 0 4 0 r
b. Trường hợp rMặt Gauss r < R OM 2 Có:   . D 4r q  e
Do bên trong quả cầu không có điện tích  0 e  hay: D E   0
c. Trường hợp r=R - có mặt Gauss r: Mặt Gauss r = R M  D O  n D 1 q 2 Có:   D.4r q E    2 e 0 4 0 R