Dự báo Thống kê: Phương pháp và Ứng dụng SPSS môn Thống kê trong kinh tế và kinh doanh | Trường Đại học Kinh Tế Quốc Dân

I I. Dự báo
Khái niệm dự báo
Dự báo cho chuỗi dừng
Dự báo cho chuỗi không dừng
Các thước đo đo độ chính xác của dự báo 21
Khái niệm dự báo
Dự báo là việc đưa ra các mức độ của hiện tượng trong tương lai với giả
định quy luật biến động trong quá khứ là không thay đổi.
Tùy thuộc vào đặc điểm của dãy số thời gian mà lựa chọn mô hình dự báo cho phù hợp.
Có thể sử dụng các thước đo đo độ chính xác của dự báo để đánh giá và lựa chọn mô hình dự báo. 22
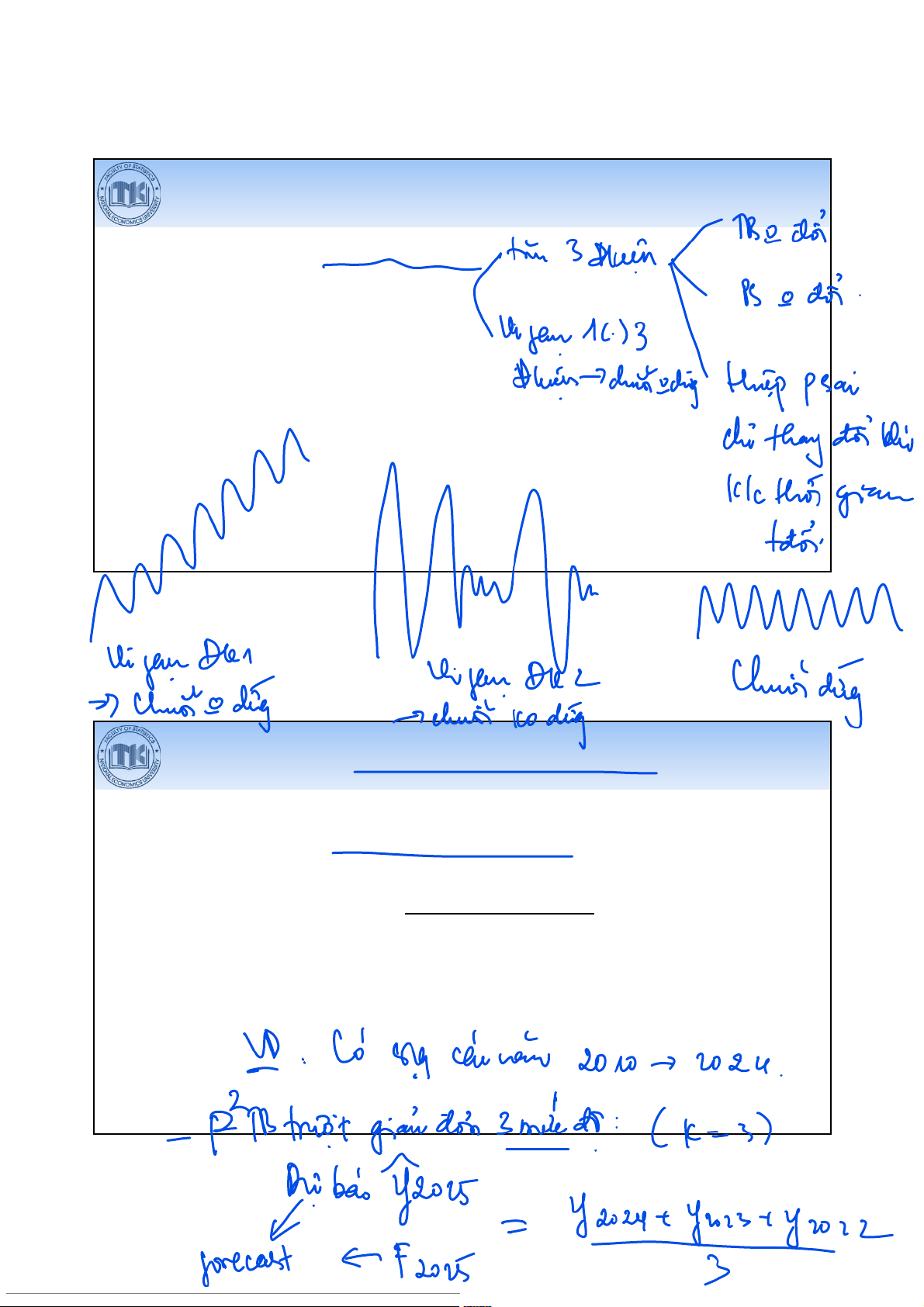
Dự báo cho chuỗi dừng
Áp dụng cho các chuỗi thời gian dừng. Các phương pháp:
• Trung bình trượt giản đơn
• San bằng mũ giản đơn 23
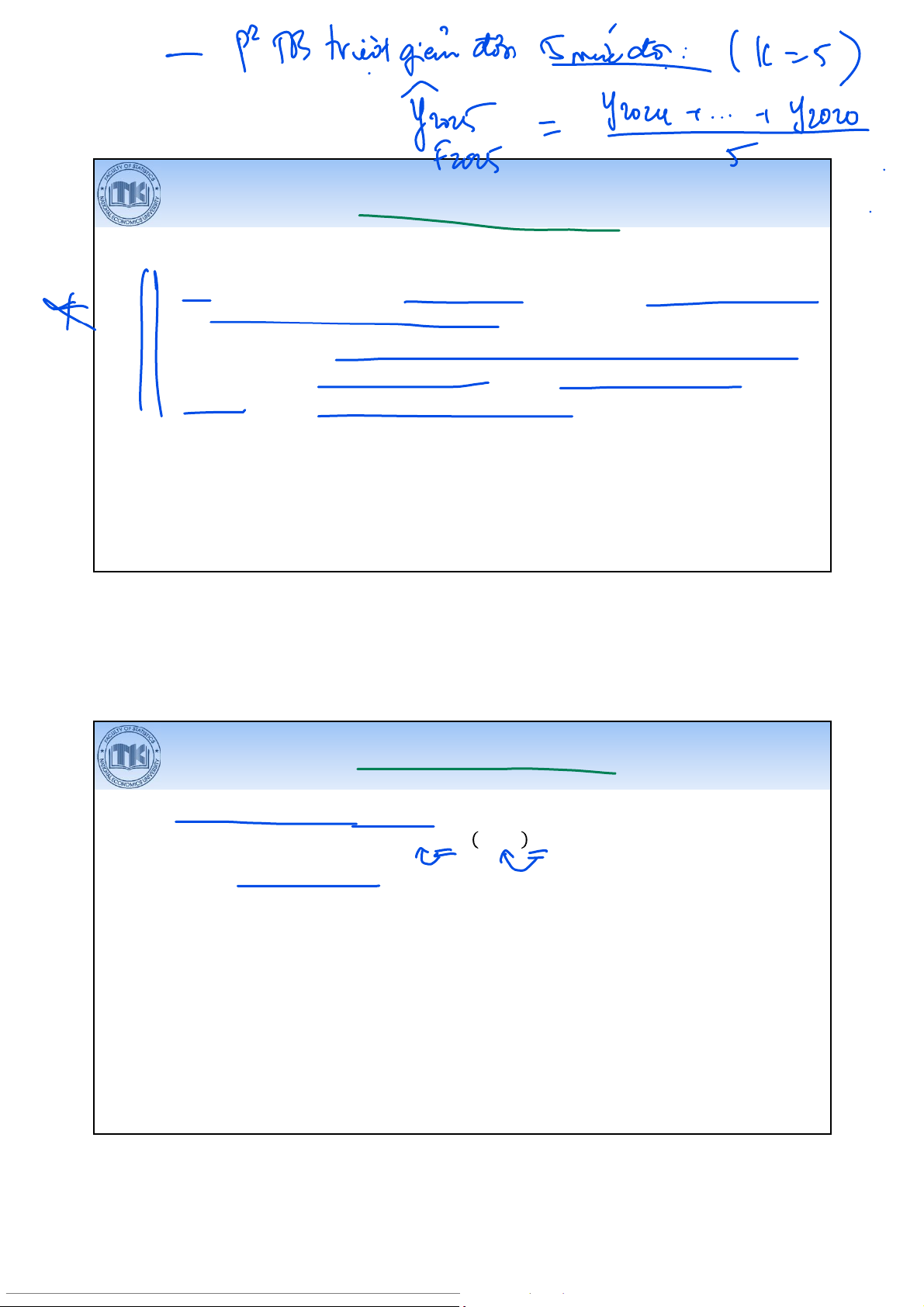
Phương pháp trung bình trượt giản đơn
Dãy số thời gian: Y1, Y2, Y3, …, Yn
Sử dụng giá trị trung bình của kthời kỳ gần nhất trong dãy số thời gian để dự
báo cho thời kỳ tiếp theo.
F =Y+ Y +⋯+ Y k
• Áp dụng quyền số như nhau cho các mức độ.
Chỉ dự báo được cho một thời kỳ tiếp theo. 24
Phương pháp trung bình trượt giản đơn
Việc lựa chọn k có thể ảnh hưởng đến kết quả dự báo.
• k lớn, dãy số trơn hơn,dự báo ổn định hơn nhưng chậm phản ứng với
những biến động trong dãy số thời gian.
• k nhỏ,dự báo sẽ phản ứng nhanh hơn với các biến động của dãy số nhưng
kết quả dự báo có thể bị ảnh hưởng bởi các biến động ngẫu nhiên hoặc
tạm thời nên không ổn định hoặc kém chính xác.
Để lựa chọn k phù hợp, có thể căn cứ vào độ chính xác của dự báo. 25
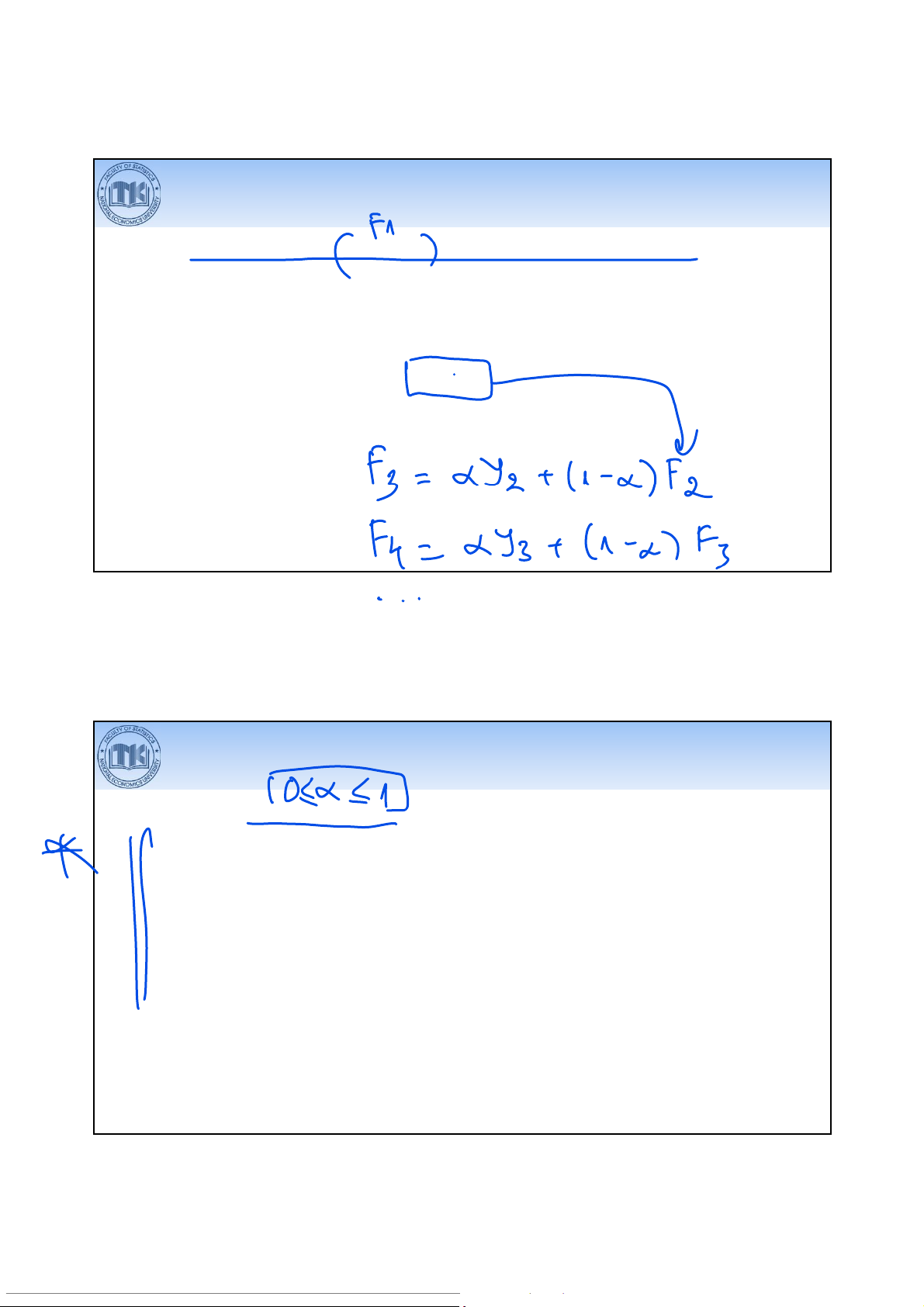
Phương pháp san bằng mũ giản đơn
Phương trình san bằng mũ giản đơn dự báo giá trị ở thời kỳ t+1:
F =αY+ 1 − α F
α:hệ số san bằng mũ, 0    1
Y: giá trị thực tế ở thời kỳ t
F: giá trị dự báo (san bằng mũ)ở thời kỳ t
• Áp dụng quyền số không bằng nhau cho các mức độ trong quá khứ 26
Phương pháp san bằng mũ giản đơn
Không thể dự báo cho kỳ đầu tiên vì không có dữ liệu ở kỳ trước đó.
Để bắt đầu tính các giá trị dự báo, cần phải gán giá trị cho kết quả dự báo của kỳ thứ hai.
• Cách phổ biến:đặt giá trị dự báo của kỳ thứ hai bằng với giá trị quan sát
thực tế của kỳ đầu tiên, tức F= Y
Chỉ dự báo được cho một thời kỳ tiếp theo. 27
Phương pháp san bằng mũ giản đơn
Giá trị của hệ số san bằng mũ có ảnh hưởng đến kết quả dự báo.
•càng gần 1, dự báo phản ứng nhanh với những thay đổi mới nhất trong
dữ liệu nhưng có thể không ổn định và dễ bị ảnh hưởng bởi những biến
động nhỏ, không liên quan đến xu hướng dài hạn.
•càng gần 0, dự báo trơn mượt,ổn định hơn và ít bị ảnh hưởng bởi các
biến động ngắn hạn nhưng khó bắt kịp với những thay đổi quan trọng hoặc
xu hướng mới của dãy số thời gian.
Có thể thử nghiệm nhiều giá trị khác nhau và lựa chọn dựa trên độ chính xác của dự báo. 28
Dự báo cho chuỗi không dừng
Áp dụng cho các chuỗi thời gian không dừng: có xu thế và không có mùa vụ. Các phương pháp:
•Dự báo dựa vào lượng tăng (giảm)tuyệt đối bình quân
•Dự báo dựa vào tốc độ phát triển bình quân
•Dự báo dựa vào ngoại suy hàm xu thế 29
Dự báo dựa vào lượng tăng (giảm) tuyệt đối bình quân
Mô hình dự báo: F = Y+δ .h Trong đó:
Yn: Mức độ cuối cùng trong dãy số h: tầm xa dự báo
Áp dụng khi dãy số có các lượng tăng (giảm)tuyệt đối liên hoàn xấp xỉ nhau 30
Dự báo dựa vào tốc độ phát triển bình quân
Mô hình dự báo: F = Y(t) Trong đó:
Yn:Mức độ cuối cùng trong dãy số h: tầm xa dự báo
Áp dụng khi dãy số có các tốc độ phát triển liên hoàn xấp xỉ nhau. 31
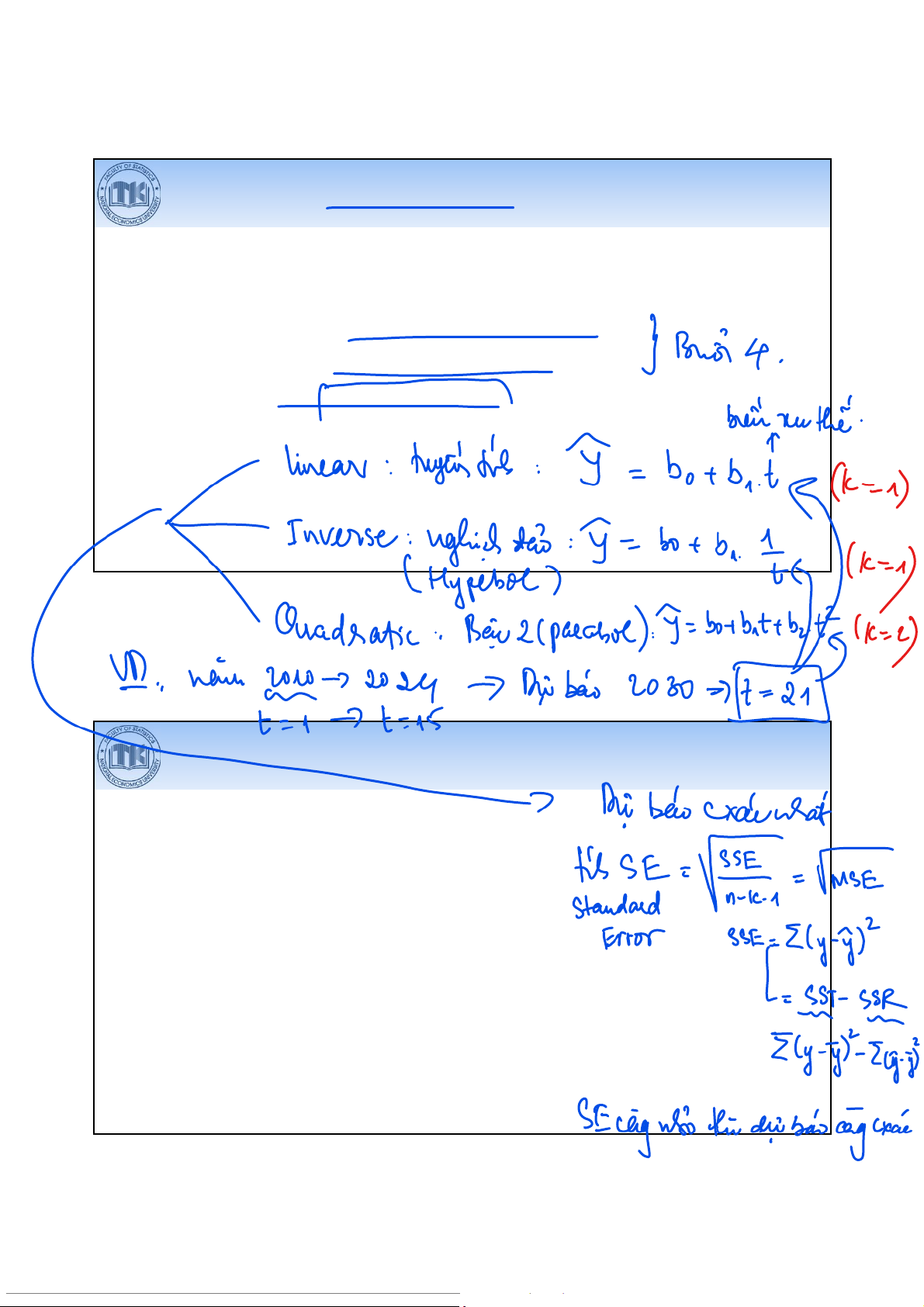
Dự báo dựa vào ngoại suy hàm xu thế
Xây dựng hàm xu thế phản ánh xu hướng biến động của hiện tượng qua thời gian: Y = f(t)
• Hàm xu thế tuyến tính • Hàm xu thế phi tuyến
Sử dụng hàm xu thế để dự báo cho các thời kỳ tiếp theo: F= Y 32
Dự báo dựa vào ngoại suy hàm xu thế
Hàm xu thế tuyến tính: Y= a + bt
Trong đó: Ylà giá trị dự báo theo xu thế tuyến tính ở thời gian t a là hệ số chặn b là hệ số góc t là thứ tự thời gian 33
Dự báo dựa vào ngoại suy hàm xu thế
Hàm xu thế tuyến tính: Y= a + bt
Ước lượng a, b theo phương pháp bình phương nhỏ nhất  b =   ∑ ∑   a = Y −bt 
Trong đó: Ylà giá trị quan sát thực tế ở kỳ t
n là số thời kỳ trong dãy số thời gian
Ylà giá trị trung bình của dãy số thời gian
tlà giá trị trung bình của t 34
Dự báo dựa vào ngoại suy hàm xu thế Hàm xu thế phi tuyến •Nghịch đảo:Y = a + b  •Bậc 2: Y = a + bt + bt •Mũ:Y = ab •Tuyến tính – log: Y= a + bln (t)
• Log – tuyến tính: ln Y= a + bt 35
Dự báo dựa vào ngoại suy hàm xu thế
Có thể sử dụng phần mềm để xác định các hàm xu thế phù hợp và lựa chọn
hàm xu thế tốt nhất để thực hiện dự báo.
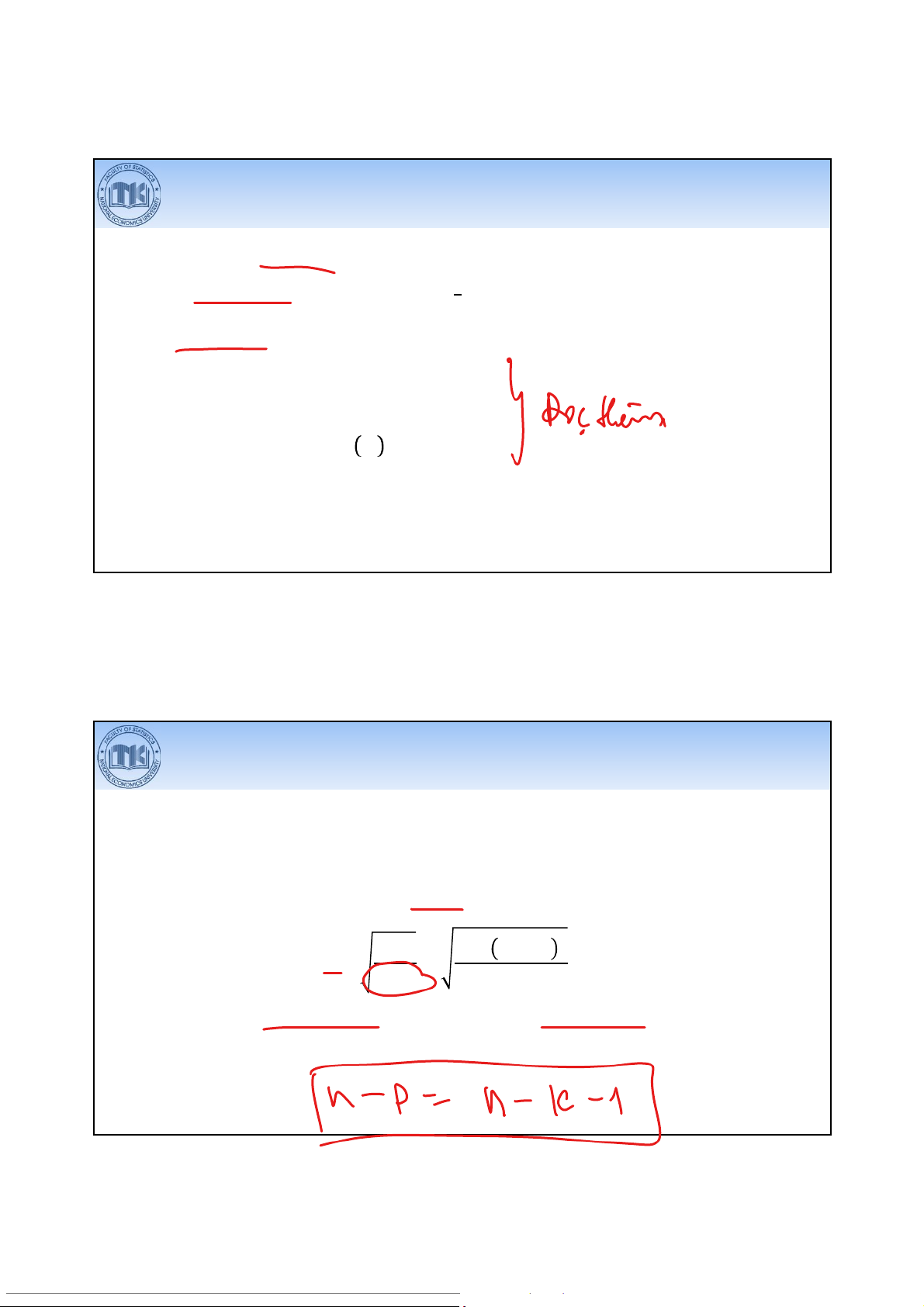
• Hàm xu thế tốt nhất được chọn trong các hàm xu thế phù hợp, có sai số
chuẩn của ước lượng (Se) nhỏ nhất. Se = SSEn  −p=∑Y  −Y  n−p⇒min
Trong đó: p là số hệ số trong hàm xu thế (gồm cả hệ số chặn) 36
Các thước đo đo độ chính xác của dự báo
Sai số dự báo (Forecast Error - FE) là sự khác biệt giữa giá trị quan sát thực
tế (Y) và giá trị dự báo (F). FE= Y−F
Sai số tuyệt đối trung bình (Mean Absolute Deviation/Error – MAD/MAE) MAD = ∑Y     −  F n=∑FE n 37
Các thước đo đo độ chính xác của dự báo
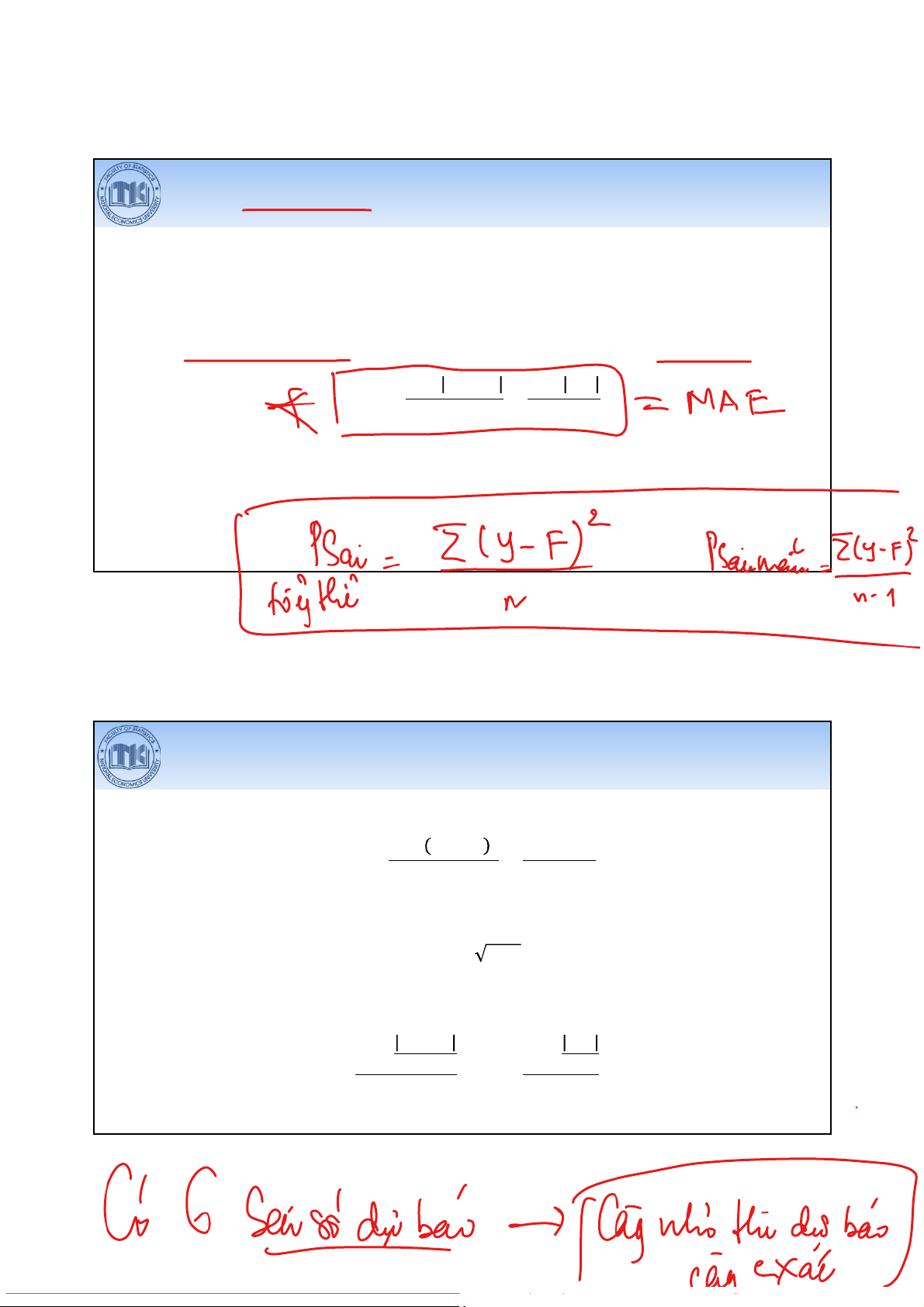
Sai số bình phương trung bình (Mean Squared Error - MSE) MSE = ∑Y   −  F n=∑FE n
Căn bậc hai của sai số bình phương trung bình (Root Mean Squared Error - RMSE) RMSE = MSE
Phần trăm sai số tuyệt đối trung bình (Mean Absolute Percentage Error - MAPE) MAPE = ∑Y−F x100 = ∑FE  Y  Y n n x100 38
Ứng dụng SPSS trong phân tích DSTG và dự báo
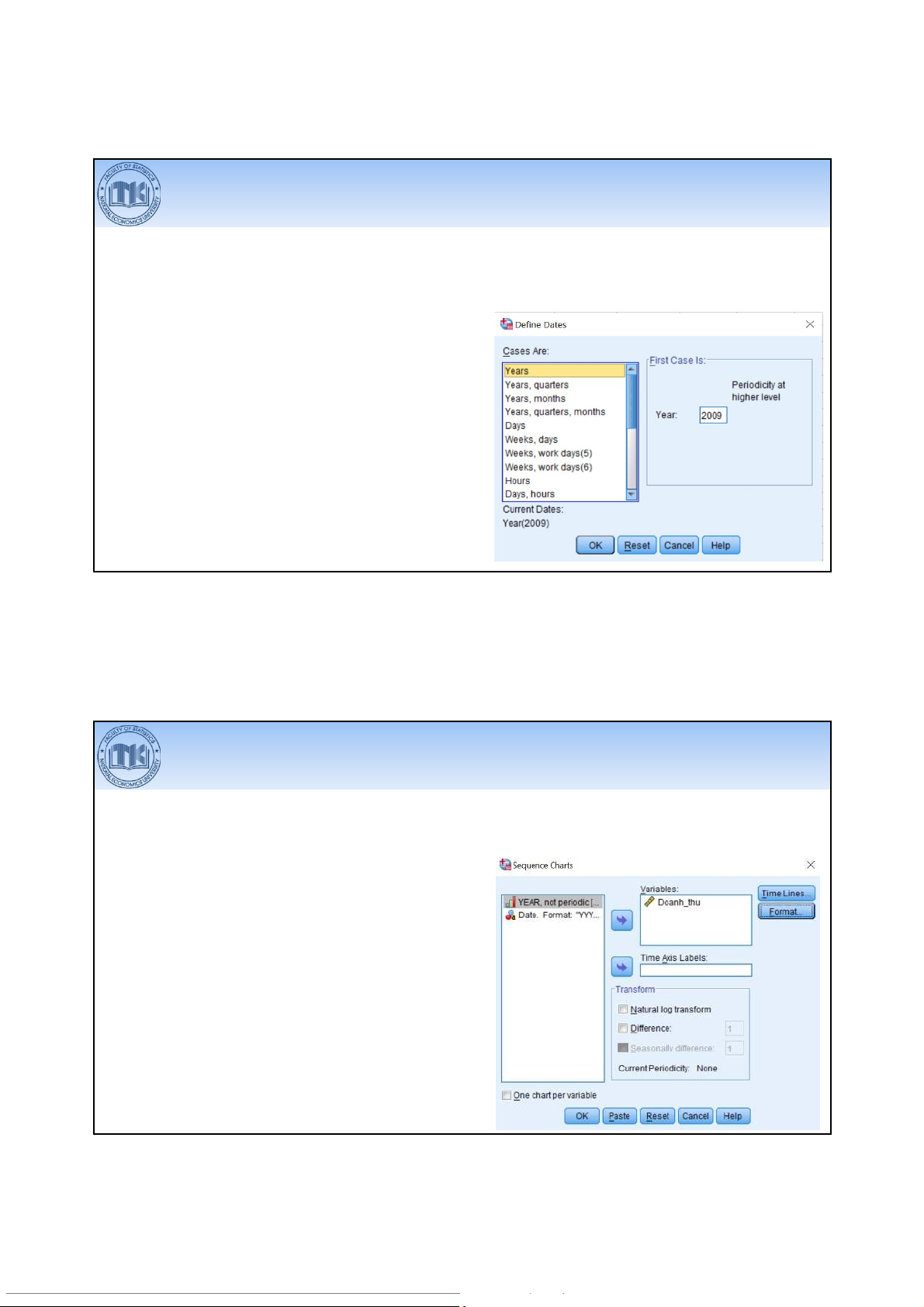
Xác định dữ liệu là chuỗi thời gian Data > Define Dates
•Chọn yếu tố thời gian phù hợp: Cases are
• Xác định kỳ đầu tiên của chuỗi: First case is 39
Ứng dụng SPSS trong phân tích DSTG và dự báo
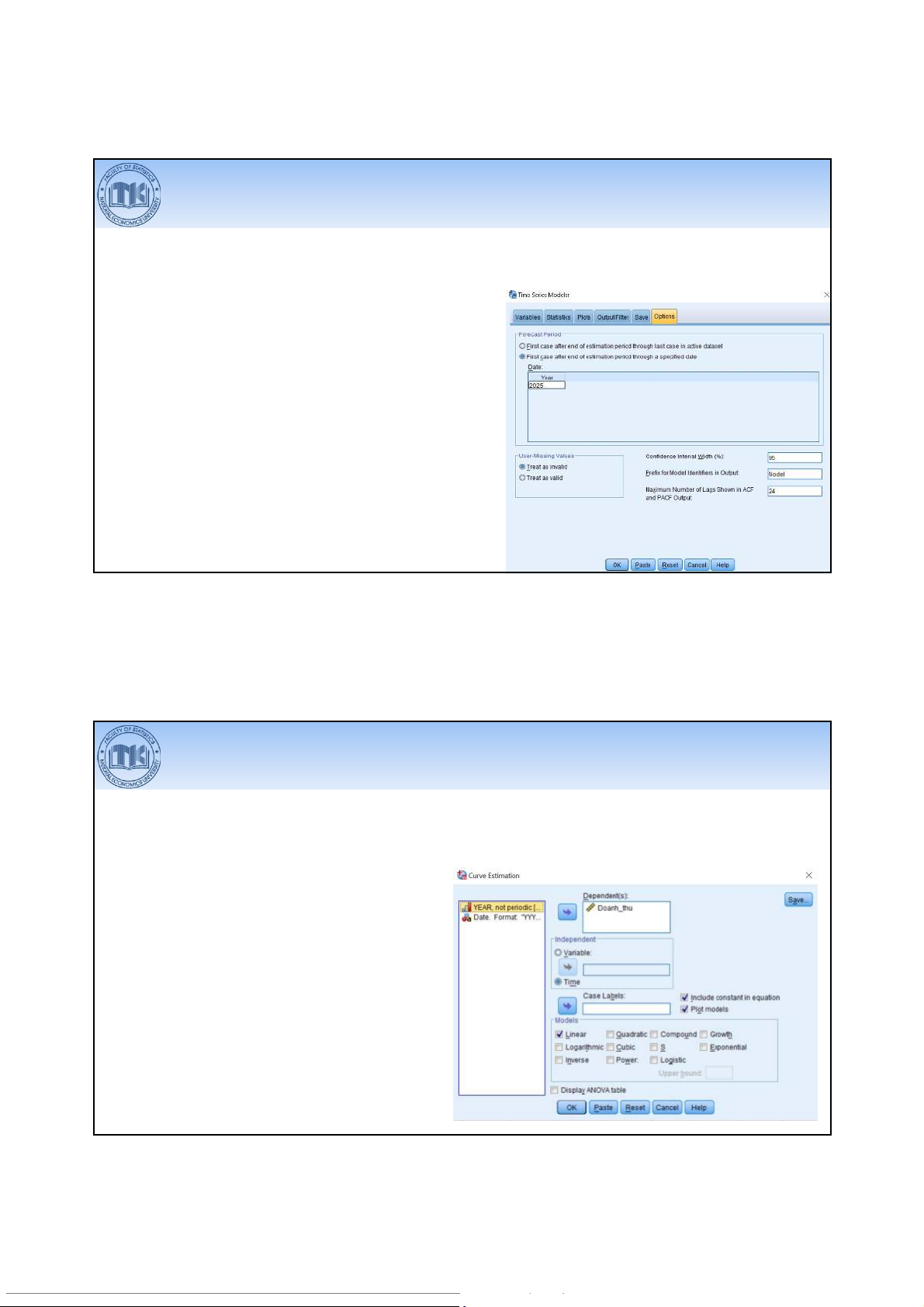
Vẽ đồ thị phát triển
Analyze > Forecasting > Sequence Charts…
•Đưa biến quan tâm vào Variables 40
Ứng dụng SPSS trong phân tích DSTG và dự báo
Dự báo bằng phương pháp san bằng mũ giản đơn
Analyze > Forecasting > Create Models… Tại khung Variables
•Đưa biến quan tâm vào Dependent Variables
•Chọn Exponential Smoothing trong Method
•Nhấn vào Criteria, chọn Model Type/ Nonseasonal/ Simple 41
Ứng dụng SPSS trong phân tích DSTG và dự báo
Dự báo bằng phương pháp san bằng mũ giản đơn
Analyze > Forecasting > Create Models… Tại khung Statistics
•Chọn các giá trị đo độ chính xác của dự báo:
Root mean square error, Mean absolute
percentage error, Mean absolute error
•Để hiển thị kết quả dự báo, chọn Display forecasts 42
Ứng dụng SPSS trong phân tích DSTG và dự báo
Dự báo bằng phương pháp san bằng mũ giản đơn
Analyze > Forecasting > Create Models… Tại khung Options
•Chọn kỳ muốn dự báo tại Forecast Period Tại khung Save
•Nếu muốn lưu lại kết quả dự báo, khoảng tin
cậy cho kết quả dự báo, phần dư, chọn
Predicted Values, Lower/Upper Confidence
Limit, Residual trong Save 43
Ứng dụng SPSS trong phân tích DSTG và dự báo
Xây dựng hàm xu thế
Analyze > Regression > Curve Estimation…
•Đưa biến quan tâm vào Dependent(s)
•Chọn Time trong Independent
•Chọn dạng hàm xu thế muốn xây dựng trong Models 44
Ứng dụng SPSS trong phân tích DSTG và dự báo
Dự báo bằng ngoại suy hàm xu thế
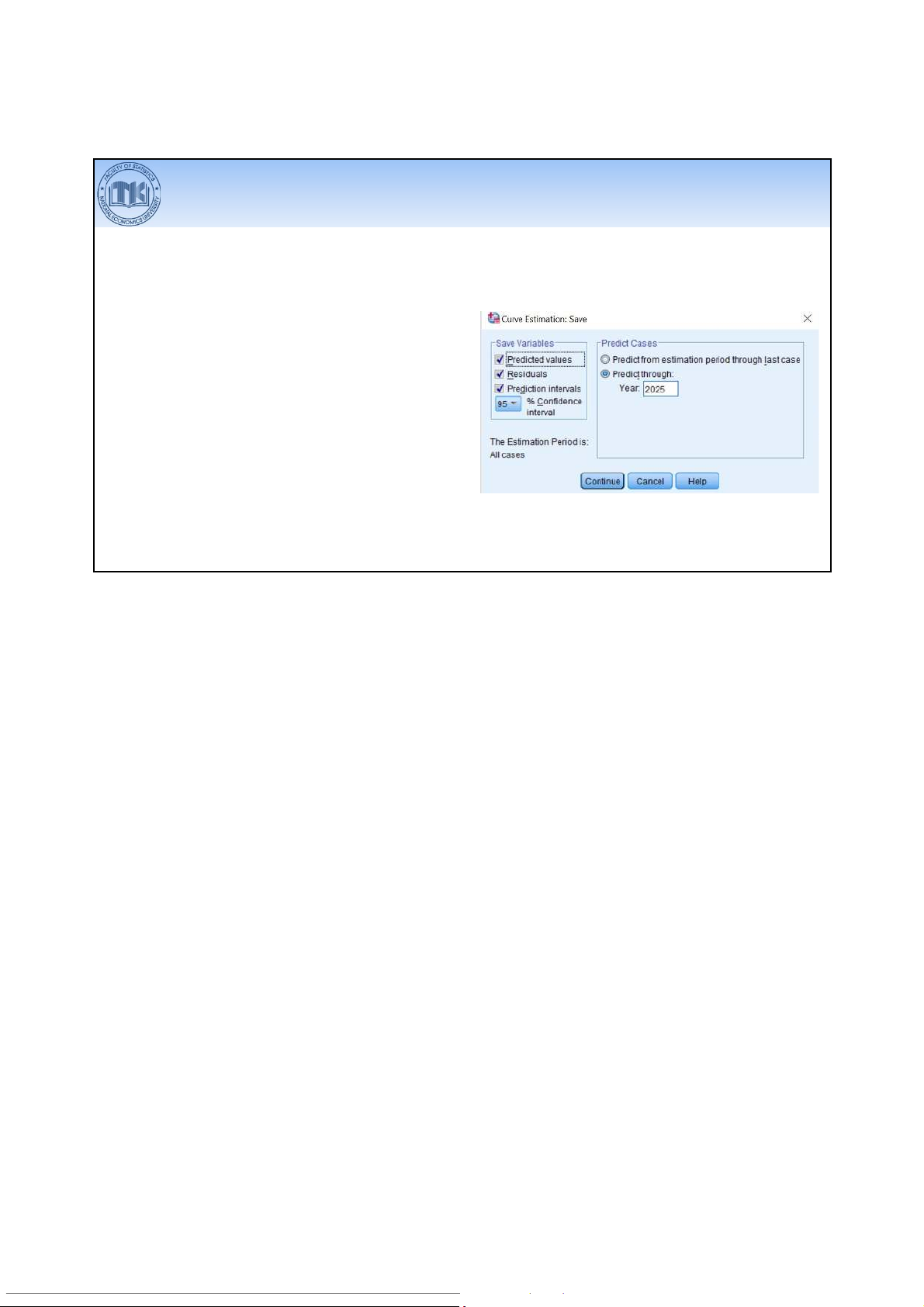
Analyze > Regression > Curve Estimation > Save
•Để lưu lại kết quả dự báo, phần dư,khoảng
tin cậy cho kết quả dự báo, tích chọn
Predicted values, Residuals và
Prediction intervals tương ứng trong Save Variables
•Chọn kỳ muốn dự báo tại Predict Cases 45