KHAI THÁC MỐI LIÊN HỆ CỦA ĐƯỜNG ĐỐI TRUNG
VỚI MỘT SỐ KHÁI NIỆM HÌNH HỌC PHẲNG
Võ Thị Ngọc Ánh, THPT chuyên Nguyễn Tất Thành, Kon Tum.
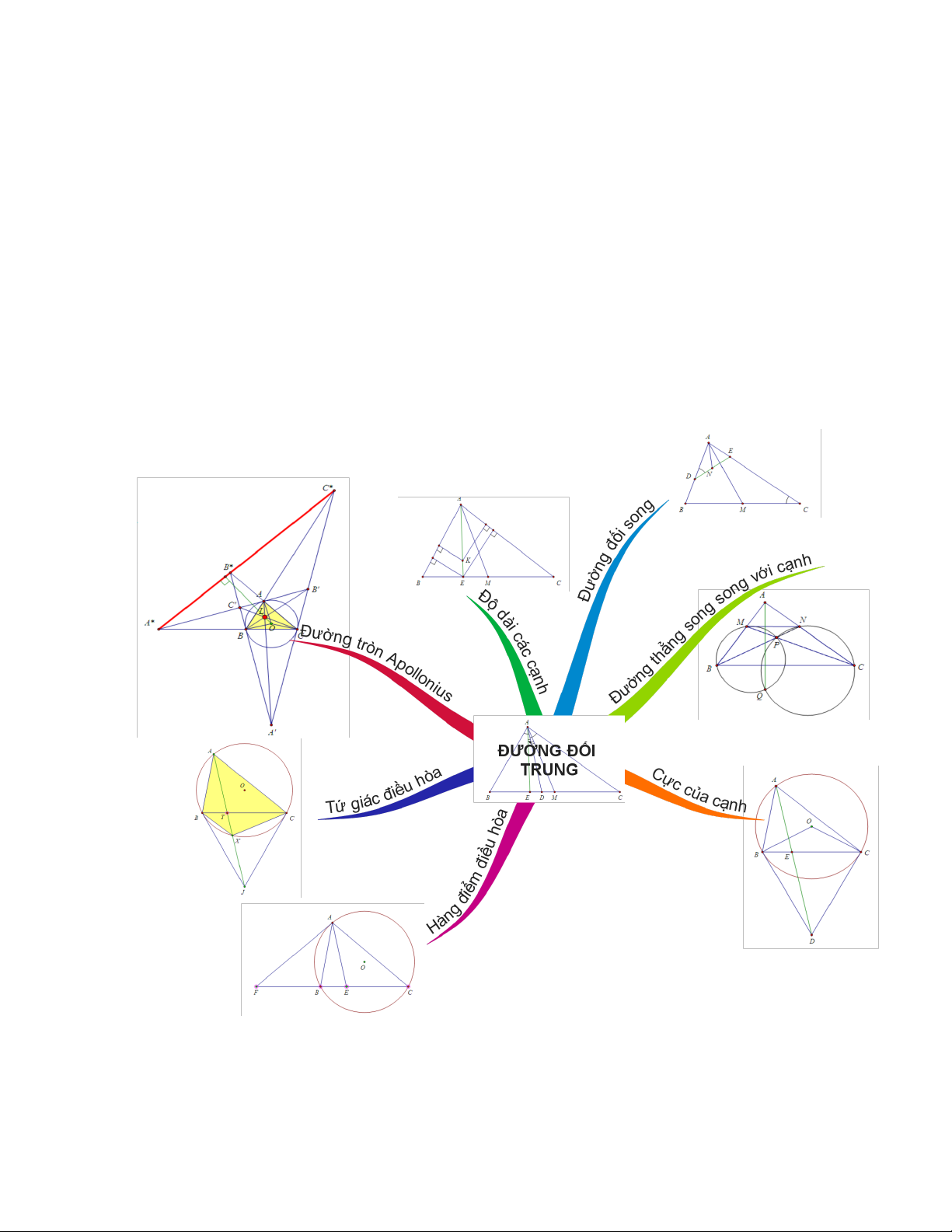
Đường đối trung là một khái niệm quan trọng trong hình học phẳng, nó
có mối liên hệ chặt chẽ với các khái niệm hình học phẳng khác như: đường
đối song, hàng điểm điều hòa, tứ giác điều hòa, cực và đối cực, ... Bài viết
này nhằm khai thác các mối liên hệ đó thông qua việc nghiên cứu mối liên
hệ giữa các yếu tố trên hình vẽ của các khái niệm trên. Về khía cạnh nào đó,
đường đối trung là "chiếc cầu nối" quan trọng để tìm tòi lời giải cho một số
bài toán hình học phẳng cũng như xây dựng các bài toán mới. 1 1
Định nghĩa đường đối trung (symmedian line)
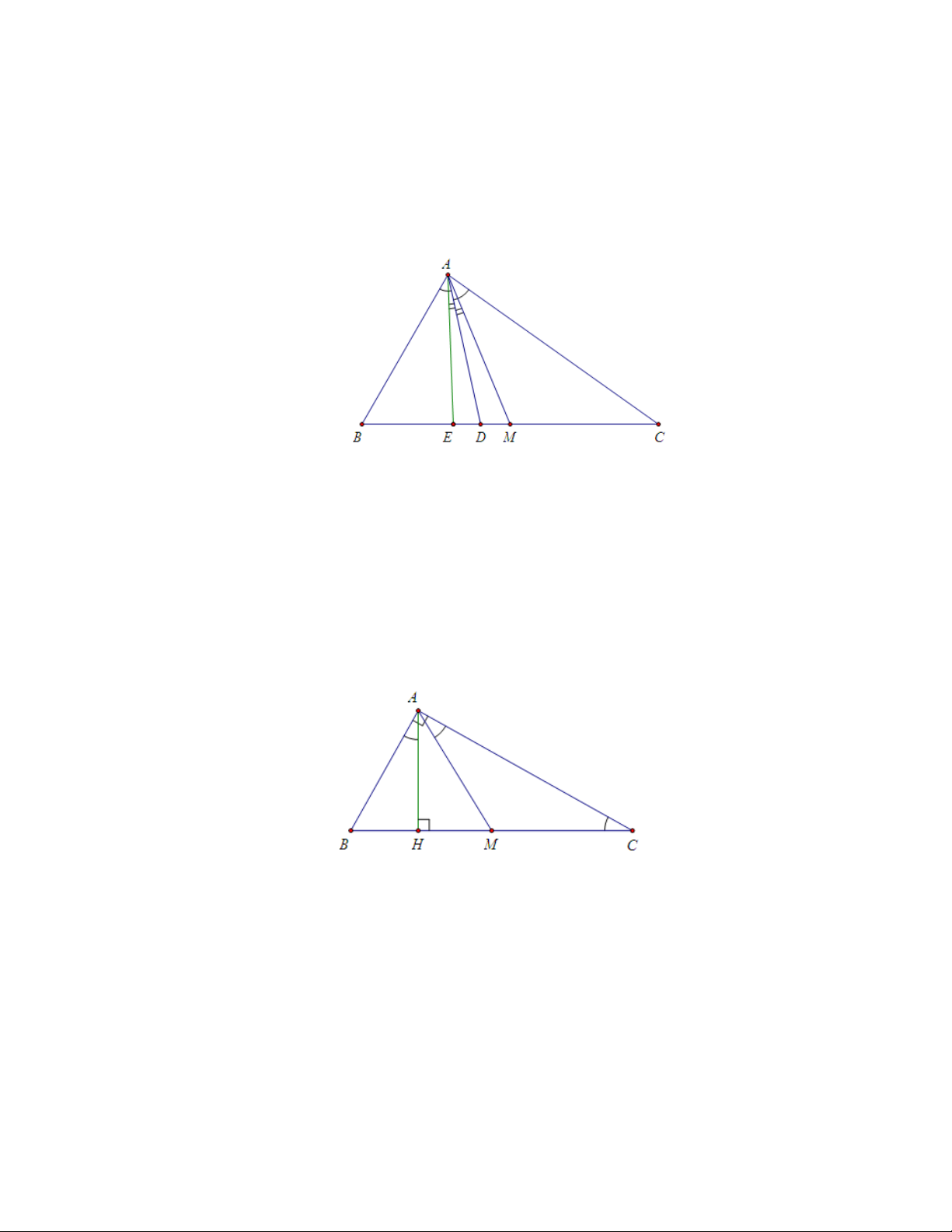
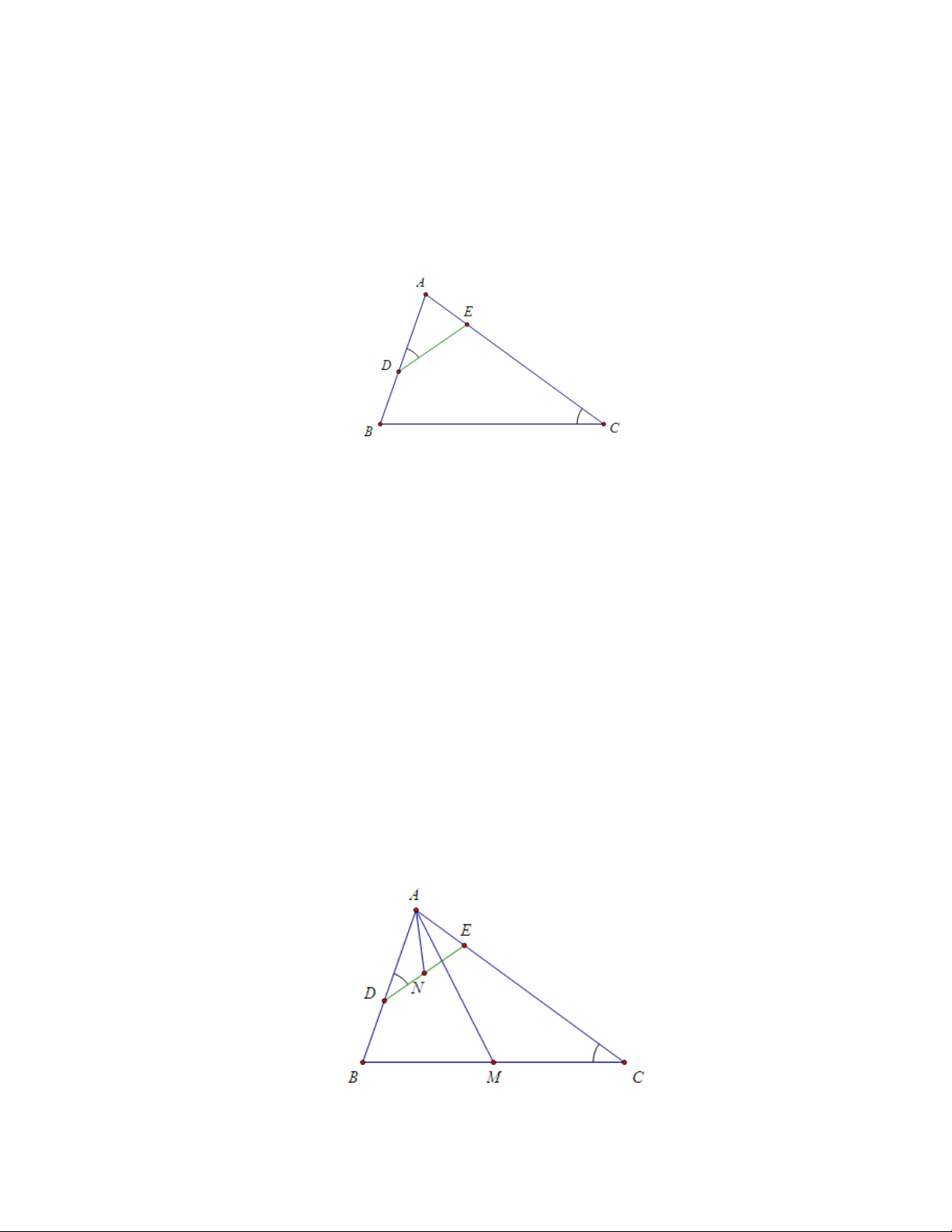
Định nghĩa 1. Trong tam giác ABC, đường thẳng AE đối xứng với đường
trung tuyến AM qua đường phân giác trong AD gọi là đường đối trung (sym-
median line) của tam giác ABC xuất phát từ đỉnh A. Nhận xét:
i) AE là đường đối trung của tam giác ABC xuất phát từ đỉnh A thì \ EAD = \ M AD, [ BAE = \ M AC, \ BAM = [ EAC .
ii) Đường đối trung AE là đường đẳng giác với đường trung tuyến AM trong góc BAC.
iii) Trong tam giác ABC vuông tại A đường cao AH chính là đường đối trung
của tam giác xuất phát từ đỉnh A. 2 2
Liên hệ giữa đường đối trung với một số khái niệm
hình học phẳng- Các dấu hiệu xuất hiện đường đối trung
Trong mục này, các kết quả được trình bày dưới dạng định lí hoặc bài
toán. Đây là các tính chất đẹp của đường đối trung, có thể là các bổ đề "tốt"
để đưa đến lời giải cho các bài toán cũng như là các ý tưởng "tốt” để xây dựng các bài toán mới. 2.1
Liên hệ giữa đường đối trung với độ dài các cạnh
của tam giác- Một số dấu hiệu cơ bản của đường đối trung 2.1.1 Dấu hiệu 1
Định lí 1. Cho tam giác ABC, E là một điểm thuộc cạnh BC. AE là đường EB AB2
đối trung của tam giác ABC khi và chỉ khi = − . EC AC2 Chứng minh: EB SBAE
* Giả sử AE là đường đối trung của tam giác ABC , ta có = − = EC SEAC 2SMAC AB sin [ BAE AB sin [ MAC AB AB2 − . = − . = − . AC.M C = − AC sin[ EAC AC sin [ MAB AC 2SMAB AC2 AB.M B EB AB2
* Giả sử E là điểm thuộc cạnh BC và = −
. Vẽ AE0 là đường đối EC AC2 E0B AB2
trung, E0 thuộc đường thẳng BC. Ta có hệ thức = − suy ra E0 ≡ E E0C AC2
hay AE là đường đối trung. Nhận xét:
i) Đường đối trung chia trong cạnh đối diện thành những phần tỉ lệ với bình EB AB2
phương các cạnh kề tức là = − . EC AC2
ii) Ba đường đối trung của tam giác đồng quy tại một điểm (do định lí Ceva),
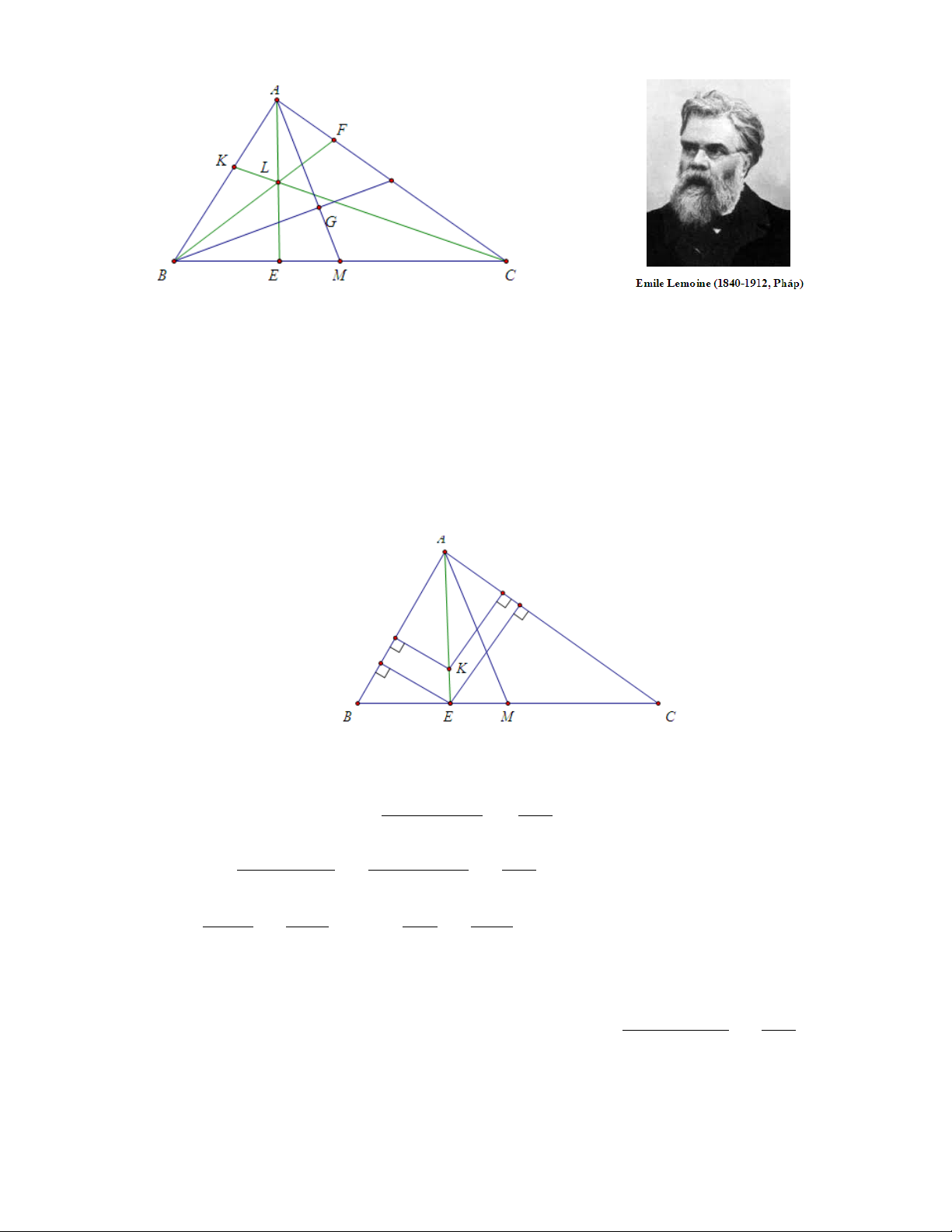
điểm này gọi là điểm Lemoine của tam giác. Như vậy, điểm Lemoine L là
điểm đẳng giác với trọng tâm G của tam giác ABC . 3 2.1.2 Dấu hiệu 2
Định lí 2. Đường đối trung xuất phát từ một đỉnh của tam giác (trừ điểm
đó) là quỹ tích của những điểm có tỉ số khoảng cách đến hai cạnh kề của tam
giác tỉ lệ thuận với độ dài của các cạnh. Chứng minh Xét tam giác ABC. d(K; AB)) AB * Gọi K là điểm sao cho =
, gọi E là giao điểm của AK và d(K; AC) AC d(E; AB)) d(K; AB)) AB BC, ta có = = . d(E; AC) d(K; AC) AC SABE AB2 EB AB2 Suy ra = , từ đó =
hay AE là đường đối trung của tam SACE AC2 EC AC2 giác.
* Ngược lại, giả sử AE là đường đối trung, dễ dàng chứng minh được điểm d(K0; AB)) AB
K0 thuộc AE (K0 không trùng với A) có tính chất = d(K0; AC) AC 4 2.2
Liên hệ giữa đường đối trung và đường đối song (antiparallel line)
Định nghĩa 2. Cho tam giác ABC. Một cát tuyến cắt hai đường thẳng AB,
AC theo thứ tự tại D và E. Nếu \ ADE = [
ACB thì ta có đoạn thẳng DE đối song với BC. Nhận xét:
i) Nếu tứ giác CBDE nội tiếp được thì DE đối song với BC.
ii) Tiếp tuyến của đường tròn ngoại tiếp một tam giác tại một đỉnh đối song với cạnh đối diện.
iii) Trong tam giác trực tâm HKL của tam giác ABC thì HKL có các cạnh
đối song với các cạnh tương ứng của tam giác. Bài toán 1.
Cho tam giác ABC. Trên đường thẳng AB lấy một điểm D và trên đường
thẳng AC lấy điểm E sao cho DE là đường đối song của BC, N là điểm
thuộc đoạn DE. Lúc đó AN là đường đối trung của tam giác ABC khi và chỉ
khi N là trung điểm của DE. Chứng minh Ta có ∆ADE ∼ ∆ACB. 5
* Giả sử N là trung điểm của DE. mà M là trung điểm của DE, BC nên ∆ADN ∼ ∆ACM suy ra \ DAN = \
CAM hay AN là đường đối trung của tam giác ABC.
* Giả sử AN là đường đối trung của tam giác ABC suy ra \ DAN = \ CAM ,
lúc đó ∆ADN ∼ ∆ACM mà M là trung điểm của BC nên N là trung điểm của DE
Nhận xét: Đường đối trung của tam giác ABC xuất phát từ A chính là
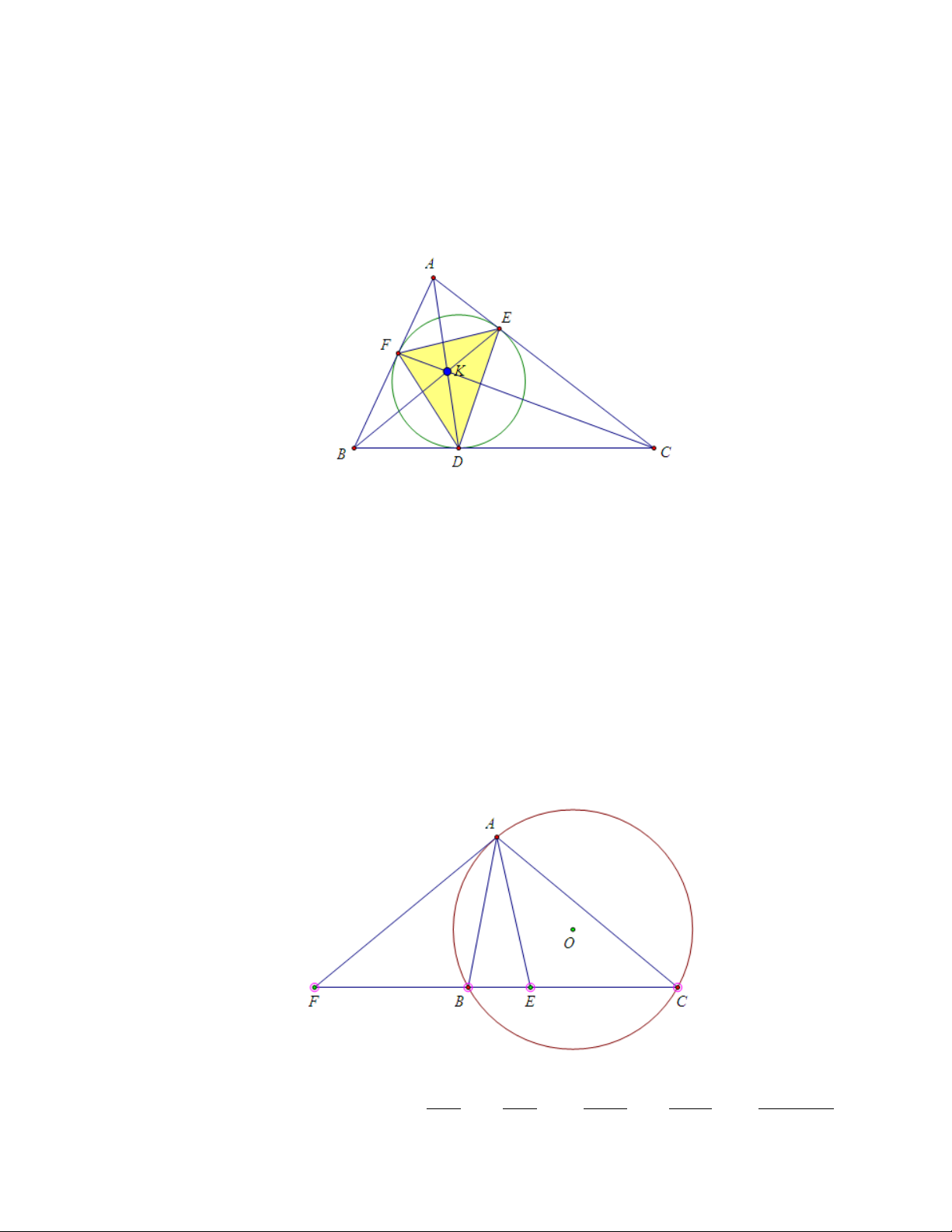
tập hợp các trung điểm của các đường đối song với cạnh BC. Bài toán 2.
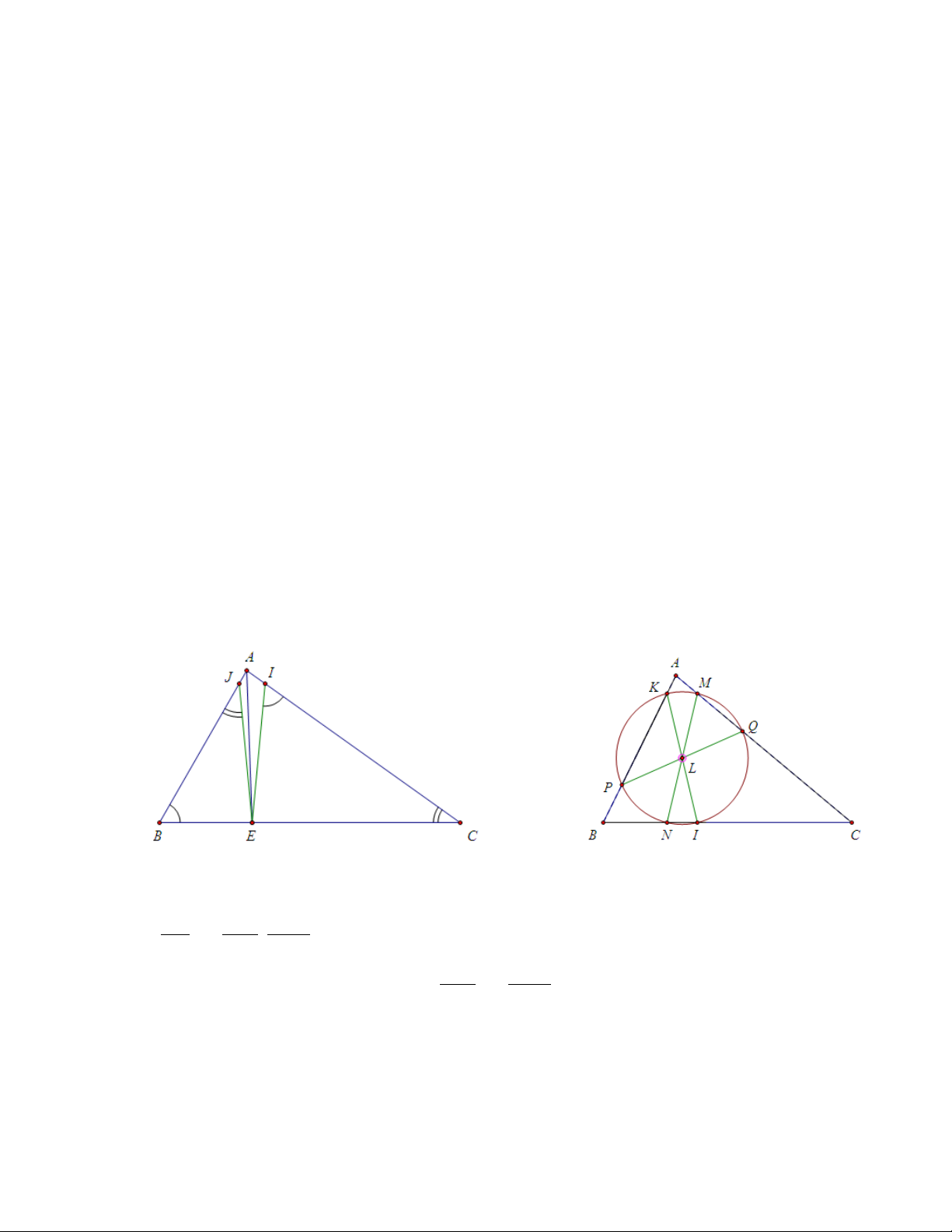
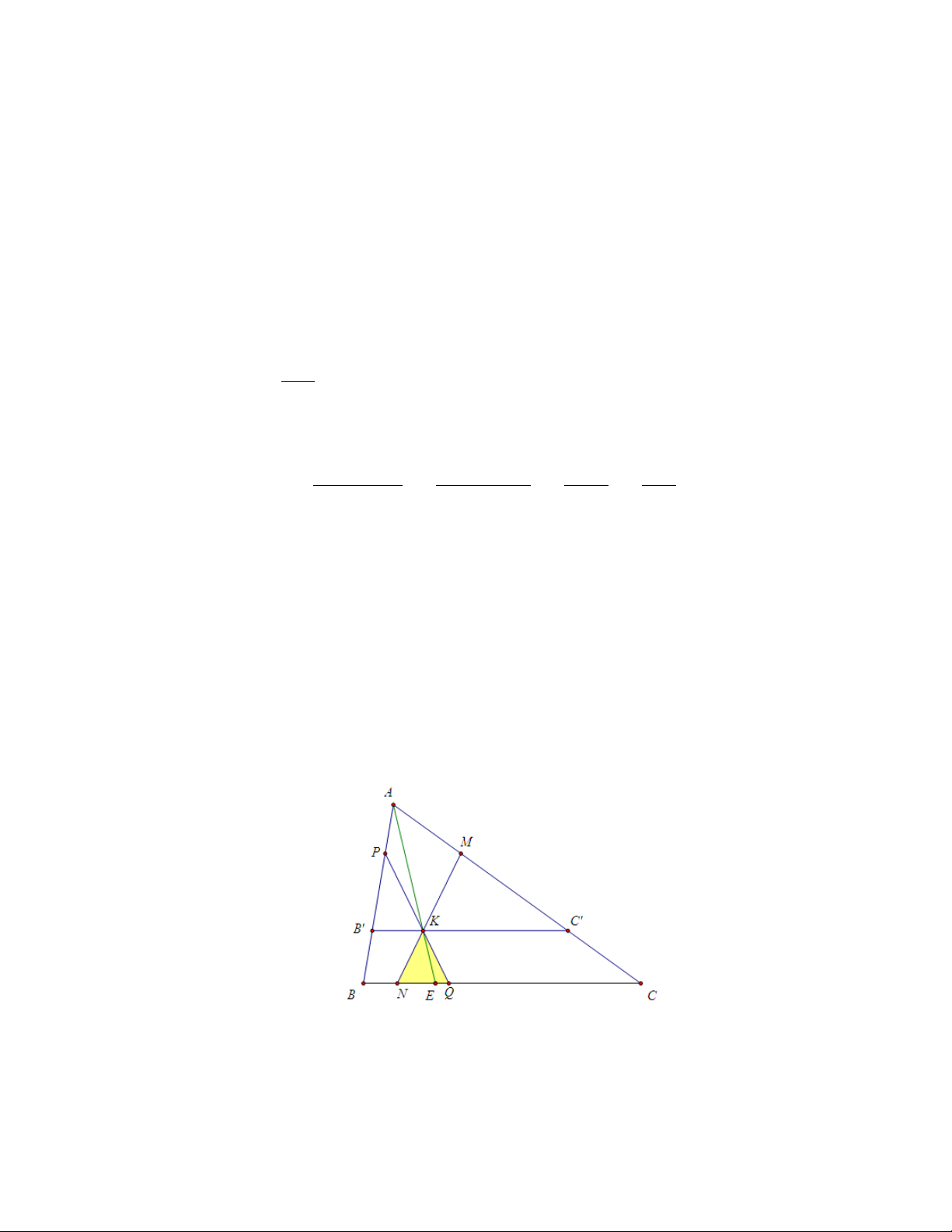
Trong tam giác ABC, E thuộc cạnh BC sao cho AE là đường đối trung, L là
điểm Lemoine của tam giác. Lúc đó:
a) Các đường đối song EJ, EI ứng với các cạnh AB, AC có độ dài bằng nhau.
b) Ba đường đối song M N , KI, P Q đi qua điểm L có độ dài bằng nhau và
nhận L làm trung điểm. Từ đó suy ra 6 điểm M, N, K, I, P, Q cùng nằm trên
một đường tròn có tâm là L (Đường tròn này gọi là đường tròn Lemoine
thứ nhất hay đường tròn Cosin hay đường tròn Tucker ). Chứng minh
a)Từ giả thiết đường đối song ta có ∆EJ B ∼ ∆ACB, ∆EIC ∼ ∆ABC suy EI EB AC2 ra = . . EJ EC AB2 EB AB2
Mà AE là đường đối trung nên = từ đó suy ra EI = EJ . EC AC2
b) Gọi ba đường đối song đi qua L là M N , P Q, KI (như hình vẽ). Ta có [ LN I = [ LIN = [
BAC nên ∆LIN cân tại L, do đó LN = LI.
Tương tự ta có LP = LK, LM = LQ.
Mặt khác, theo bài toán 1 , L là trung điểm của các đoạn thẳng M N , P Q,
KI nên LM = LN = LP = LQ = LK = LI suy ra M N = P Q = KI và 6 6
điểm M, N, P, Q, K, I cùng thuộc một đường tròn có tâm L 2.3
Liên hệ giữa đường đối trung xuất phát từ một
đỉnh tam giác và đường thẳng song song (parallel
line) với cạnh đối diện
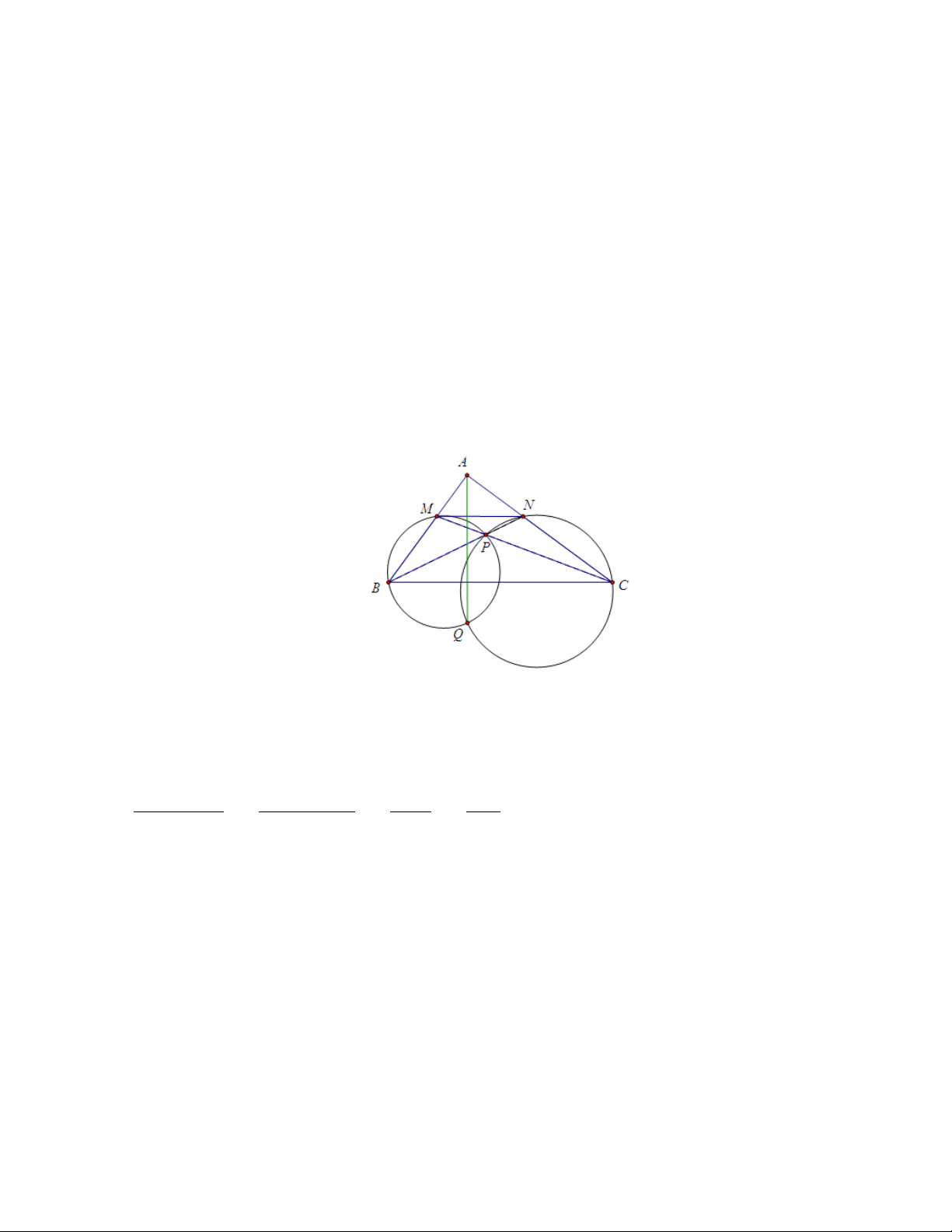
Bài toán 3. (BMO 2009) Cho M N là đường song song với cạnh BC của
tam giác ABC với M thuộc cạnh AB, N thuộc cạnh AC. Các đường thẳng
BN và CM cắt nhau tại P . Đường tròn ngoại tiếp các tam giác BM P và
CN P cắt nhau tại hai điểm P và Q. Lúc đó đường thẳng AQ là đường đối
trung xuất phát từ A của tam giác ABC. Chứng minh Ta có \ BQM = \ BP M = \ CP N = \ CQN , \ M BQ = [ CP Q = \ CN Q. Suy ra d(Q; AB) d(Q; BM ) BM AB = = =
nên theo dấu hiệu 2 , suy ra AQ là d(Q; AC) d(Q; CN ) CN AC đường đối trung
Nhận xét:Trong tài liệu [2] khai thác rất nhiều bài toán vận dụng từ mối liên hệ trên.
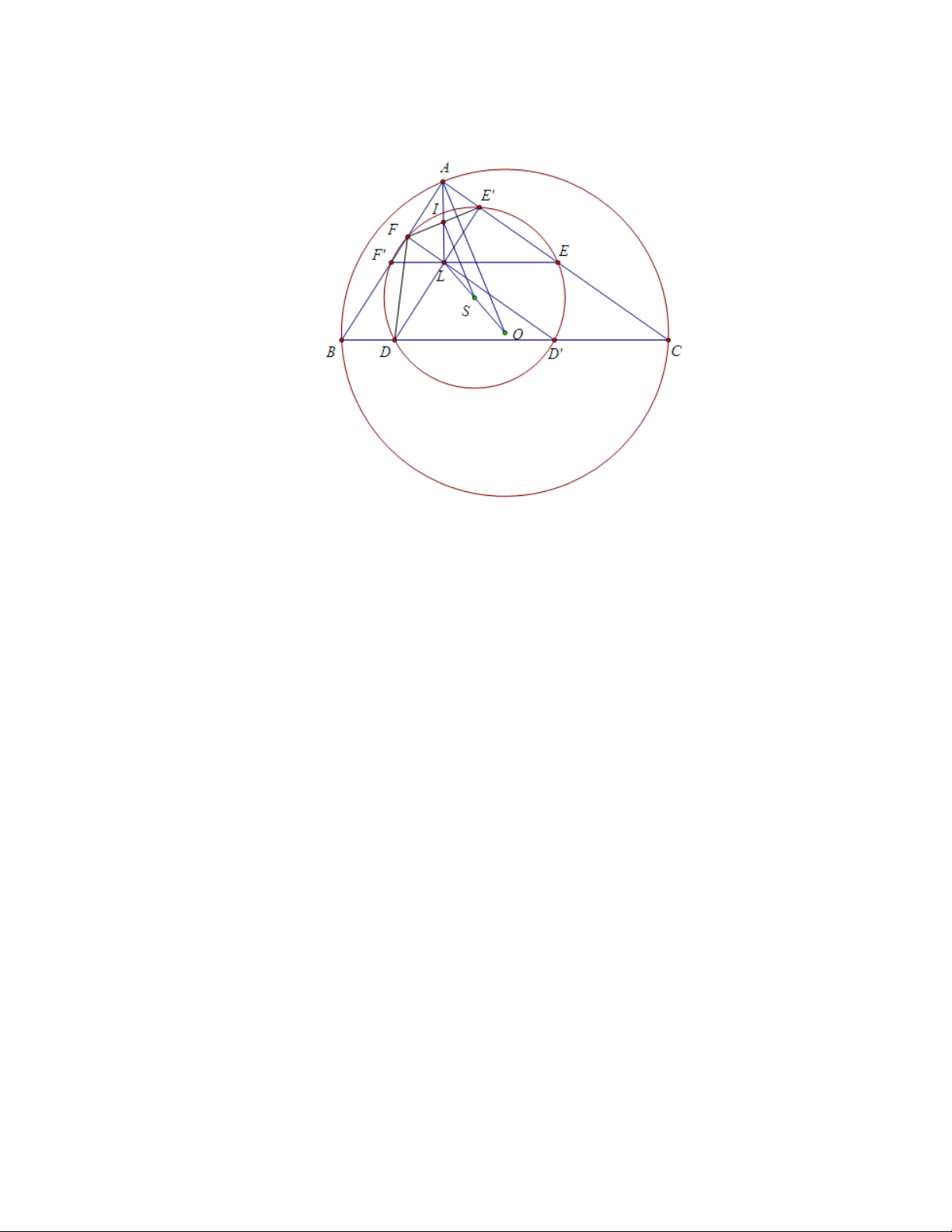
Bài toán 4. (Đường tròn Lemoine thứ hai)
Ba đường thẳng đi qua điểm Lemoine L và song song với các cạnh của tam
giác ABC xác định trên ba cạnh 6 điểm cùng thuộc một đường tròn. Đường
tròn này gọi là đường tròn Lemoine thứ hai. Tâm của đường tròn chính là
trung điểm của LO (với O là tâm ngoại tiếp của tam giác ABC). 7 Chứng minh
Gọi D, D0, E, E0, F, F 0 lần lượt là các giao điểm của các đường thẳng đi
qua điểm Lemoine và song song với các cạnh của tam giác với các cạnh BC, CA, AB.
Ta có AF LE0 là hình bình hành nên AL đi qua trung điểm của F E0, mà AL
là đường đối trung của tam giác ABC nên F E0 là đường đối song ứng với BC của ∆ABC .
Suy ra F E0 cũng là đường đối song ứng với F 0E của ∆AF 0E. Do đó E, E0, F, F 0
cùng thuộc đường tròn, ta gọi là đường tròn (Ω1).
Chứng minh tương tự, ta được E, E0, D, D0 cùng thuộc đường tròn (Ω2) và
F, F 0, D, D0 cùng thuộc đường tròn (Ω3).
Giả sử (Ω1), (Ω2), (Ω3) đôi một phân biệt thì ba trục đẳng phương AB, BC, CA
đồng quy hoặc song song (điều này mâu thuẫn) suy ra D, D0, E, E0, F, F 0 cùng
thuộc một đường tròn, ta gọi là (Ω).
Vì EF 0 đối song với BC nên EF 0⊥AO (với O là tâm đường tròn ngoại tiếp
của ∆ABC). Gọi S là trung điểm của LO thì IS k AO nên S thuộc đường
trung trực của E0F . Tương tự, S cũng thuộc đường trung trực của ED0, DF 0 hay S là tâm của (Ω) 8 2.4
Liên hệ giữa đường đối trung với cực (pole) của
cạnh tam giác ứng với đường tròn ngoại tiếp của tam giác
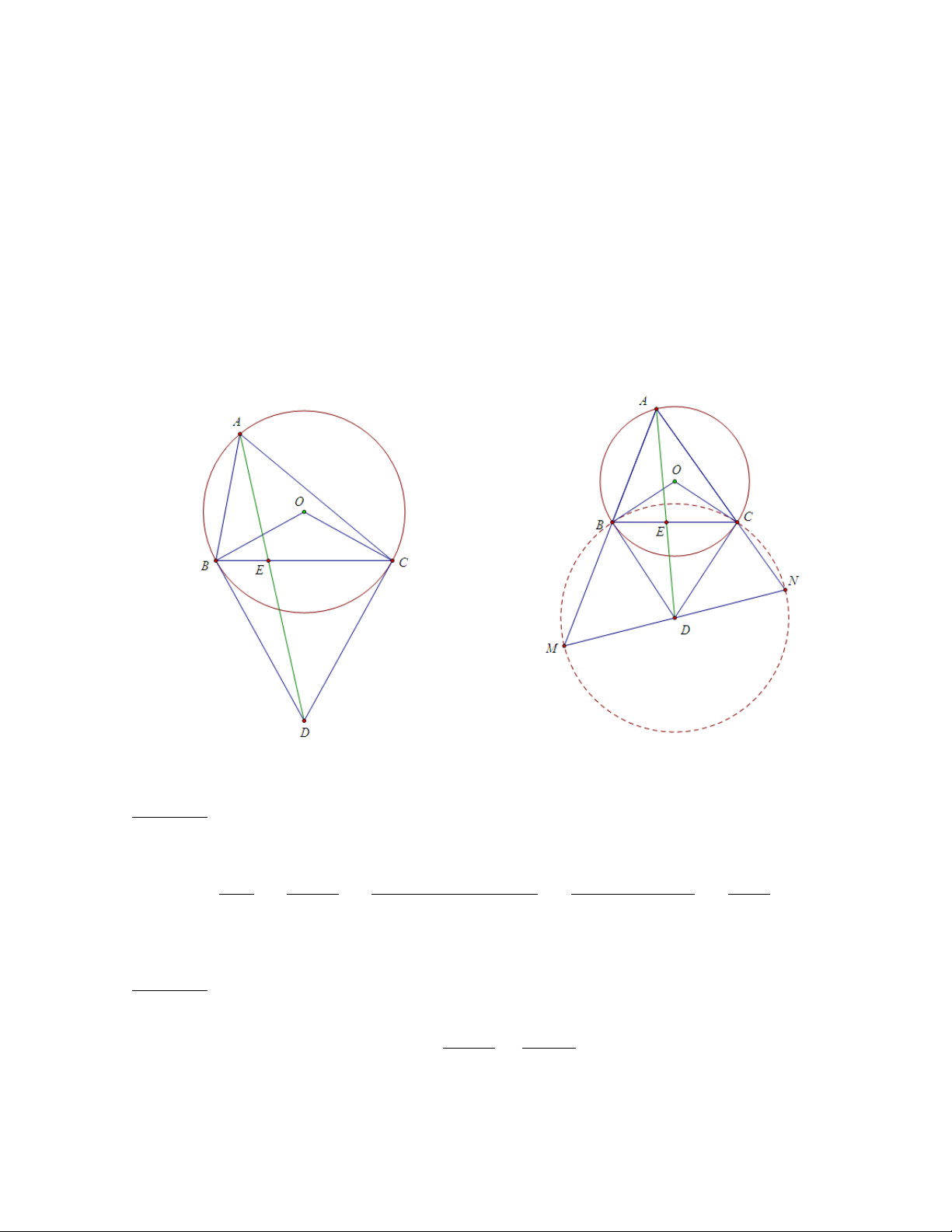
Bài toán 5. Cho tam giác ABC nội tiếp đường tròn (O), E là điểm thuộc
cạnh BC. Lúc đó AE là đường đối trung khi và chỉ khi AE đi qua cực của BC
ứng với đường tròn (O) (tức là, đường đối trung xuất phát từ A đi qua giao
điểm của hai tiếp tuyến tại B, C của đường tròn (O) ). Chứng minh
Giả sử D là cực của BC ứng với (O). Ta cần chứng minh AD là đường đối trung của tam giác ABC. Cách 1: Ta có: EB SABD AB.BD.sin\ ABD AB.sin\ ABD AB2 = = = = . EC SACD AC.CD.sin\ ACD AC.sin\ ACD AC2
Nên theo dấu hiệu 1, AE là đường đối trung của tam giác.
Cách 2: Gọi M, N là giao điểm của AB, AC với đường tròn Ω tâm D bán kính DB. \ BOC \ BDC Ta có \ M BN = \ BAN + \ AN B = +
= 900 nên M N là đường kính 2 2
của đường tròn, nên D là trung điểm của M N mà BC đối song với M N nên
theo bài toán 1, AD là đường đối trung của tam giác ABC 9
Nhận xét: Nếu D, E, F là tiếp điểm của đường tròn nội tiếp với các cạnh
BC, CA, AB của tam giác ABC (DEF còn được gọi là tam giác Gergonne
của tam giác ABC) thì DA, EB, F C là các đường đối trung của tam giác
DEF . Tức là điểm Gergonne của tam giác ABC chính là điểm Lemoine của tam giác Gergonne. 2.5
Liên hệ giữa đường đối trung với hàng điểm điều hòa (Harmonic division)
Bài toán 6.Cho tam giác ABC nội tiếp (O), điểm E thuộc cạnh BC, BC
giao với tiếp tuyến tại A của (O) tại F. Lúc đó, AE là đường đối trung xuất
phát từ A của tam giác ABC khi và chỉ khi (BCFE)=-1. Tiếp tuyến AF còn
gọi là đường đối trung ngoài của tam giác ABC. Chứng minh F B AB F B2 AB2 F B2 Ta có ∆AFB ∼ ∆CF A nên = ⇒ = ⇒ = F A AC F A2 AC2 F B.F C 10 AB2 F B AB2 ⇒ = . AC2 F C AC2
(Để ý, vì F A là tiếp tuyến nên F A2 = F B.F C). Suy ra EB AB2 F B EB
AE là đường đối trung ⇔ = ⇔ = ⇔ (BCF E) = −1 EC AC2 F C EC
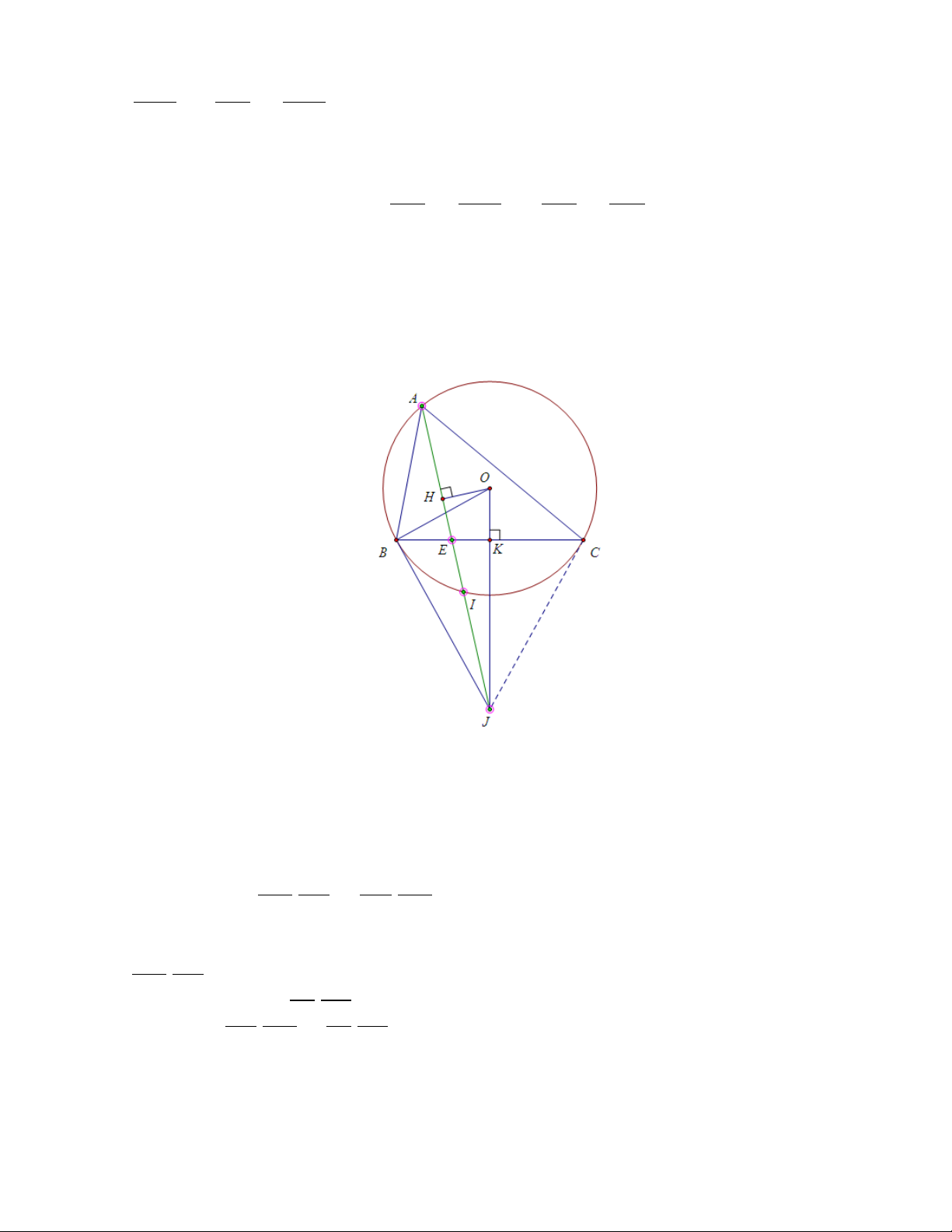
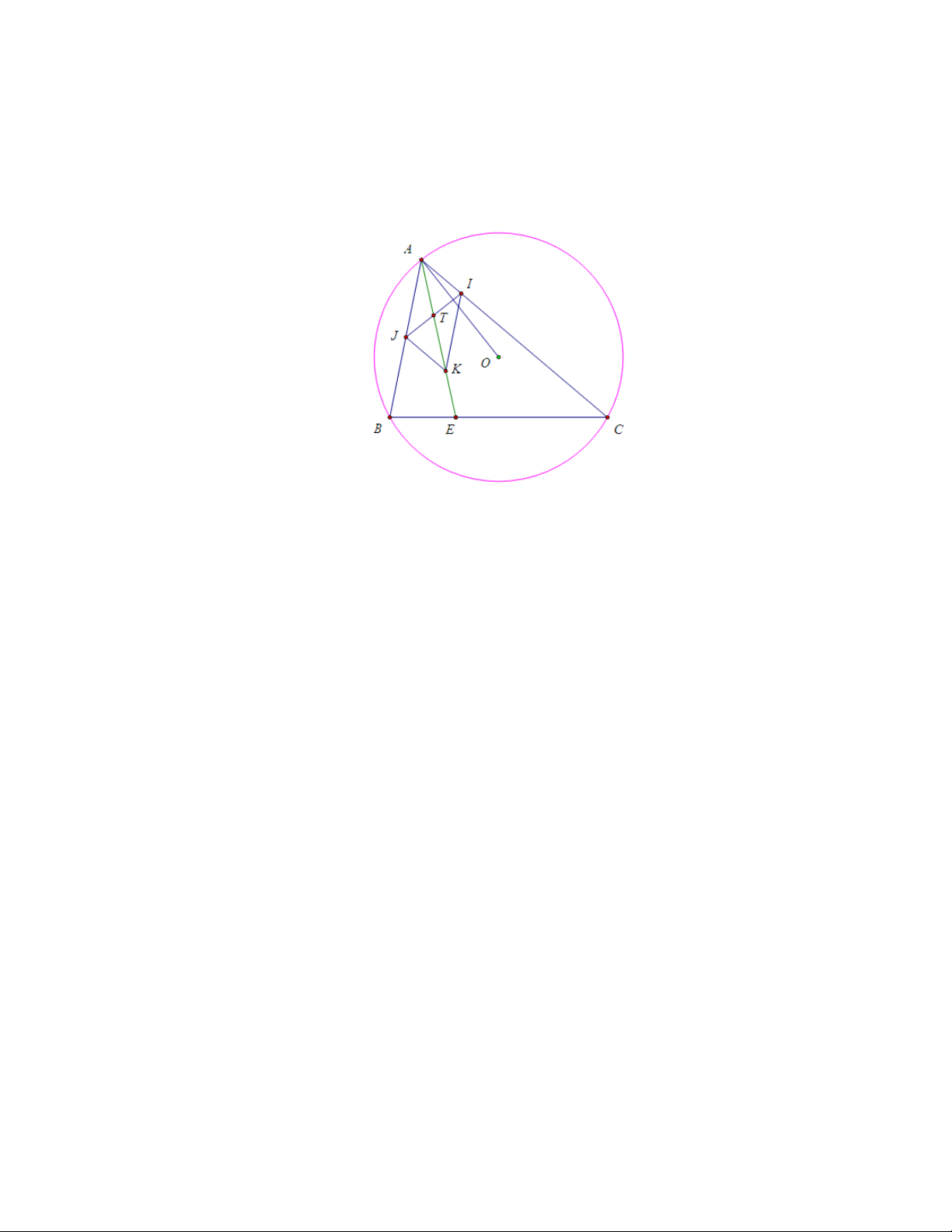
Bài toán 7.Cho tam giác ABC nội tiếp (O), đường đối trung xuất phát từ A
cắt cạnh BC tại E, AE cắt tiếp tuyến tại B của (O) tại J và cắt đường tròn
(O) tại I (I khác A) thì (AIEJ)=-1. Chứng minh
Theo bài toán 5 , AE là đường đối trung và AE cắt tiếp tuyến tại B của
(O) tại J nên J cũng là giao điểm của hai tiếp tuyến của (O) tại B và C.
Gọi H là hình chiếu của O lên AJ , nên H là trung điểm của AI.
Đặt K là giao điểm của OJ và BC. Ta có, tứ giác OHEK nội tiếp (vì \ OHE = \ OKE = 900).
Suy ra ta có J K.J O = J E.J H (phương tích của điểm J đối với đường tròn ngoại tiếp OHEK)
Mặt khác xét trong tam giác OBJ vuông tại B có BK là đường cao thì J K.J O = J B2.
Hơn nữa J B2 = J I.J A (phương tích của điểm J đối với đường tròn (O)). Từ
đó suy ra J E.J H = J I.J A nên theo hệ thức Macloranh suy ra (AIEJ ) = −1 11 2.6
Liên hệ giữa đường đối trung với tứ giác điều hòa (harmonic quadrilateral)
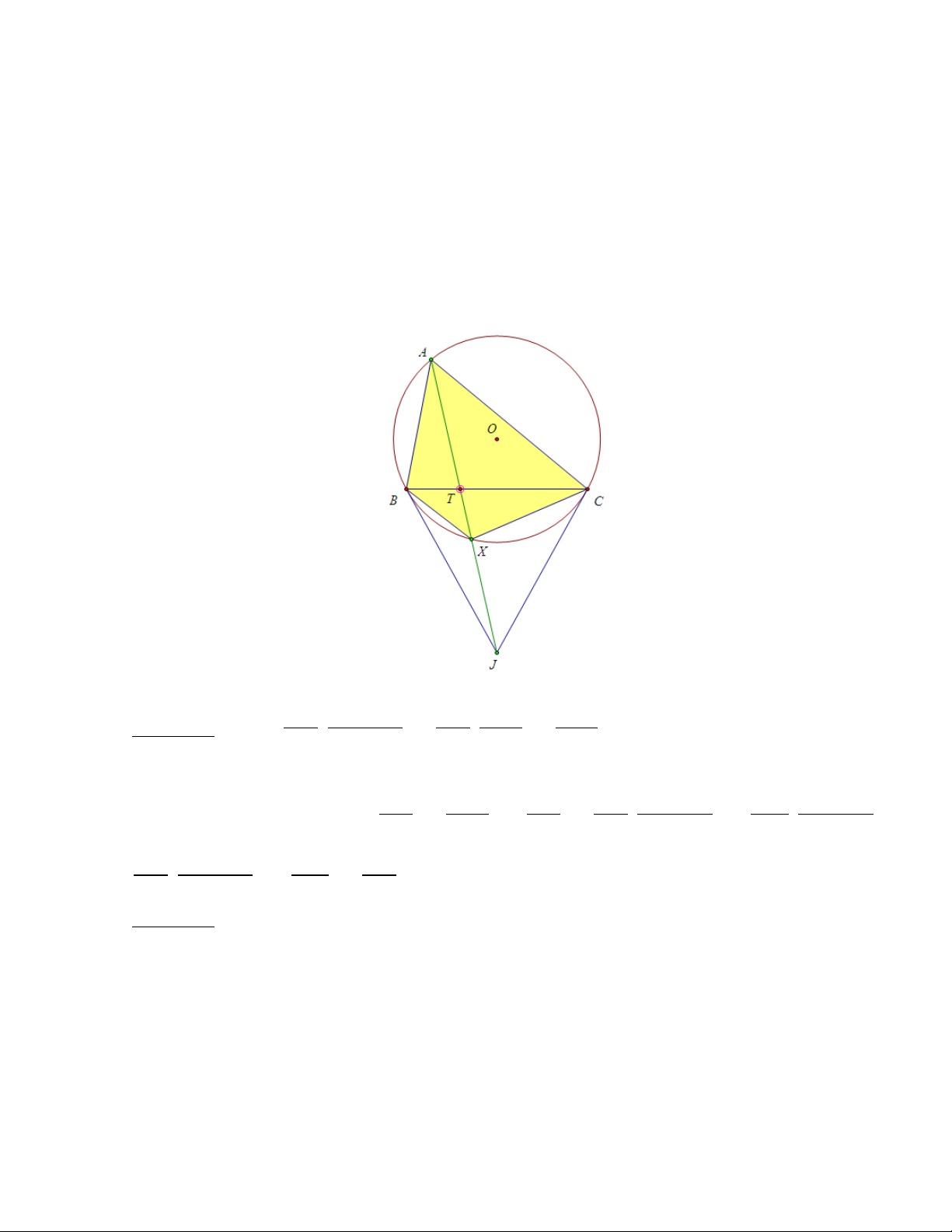
Bài toán 8. Cho tam giác ABC nội tiếp đường tròn (O), X là điểm thuộc
cung BC không chứa A. Lúc đó AX là đường đối trung của tam giác ABC
khi và chỉ khi tứ giác ABXC điều hòa. Chứng minh AB sin [ AXB AB sinb C AB2 Cách 1: Ta có . = . = AC sin [ AXC AC sin AC2 b B
Gọi T là giao điểm của AX với BC. Ta có T B AB2 T B AB sin [ AXB XB sin [ AXB
AX là đường đối trung ⇔ = ⇔ = . ⇔ . = T C AC2 T C AC sin [ AXC XC sin [ AXC AB sin [ AXB XB AB . ⇔ =
⇔ABXC là tứ giác điều hòa. AC sin [ AXC XC AC
Cách 2: ABXC là tứ giác điều hòa ⇔ AX đi qua giao điểm hai tiếp tuyến
tại B và C của (ABC) ⇔ AX là đường đối trung (theo bài toán 5 ) 2.7
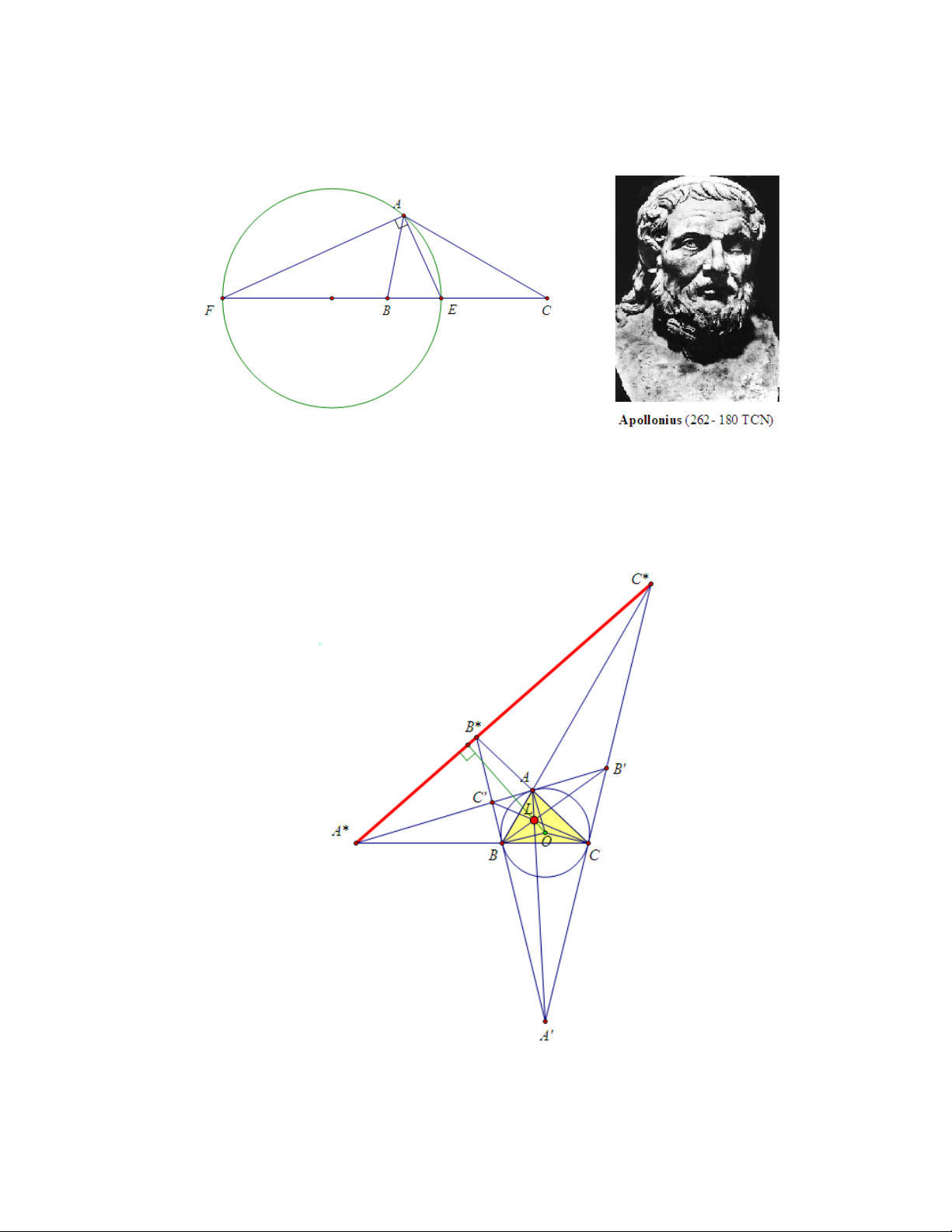
Liên hệ giữa đường đối trung và đường tròn Apol- lonius (Apollonius Circle)
Định nghĩa 3. Cho tam giác ABC không cân, nếu các phân giác trong và
phân giác ngoài góc A cắt cạnh BC tại E và F thì đường tròn đường kính EF 12
gọi là đường tròn A- Apollonius. Tương tự ta có các đường tròn B- Apollonius, C- Apollonius.
Nhận xét: Gọi (O) là đường tròn ngoại tiếp ∆ABC, xét cực và đối cực đối với (O)
i) Gọi A∗ là giao điểm của tiếp tuyến tại A của đường tròn (O) và BC, khi
đó A∗ là tâm của đường tròn A - Apollonius. Tương tự, ta có các điểm B∗,
C∗ . Để ý rằng ở đây AA∗, BB∗, CC∗ chính là các đường đối trung ngoài của tam giác ABC. 13
ii) Gọi A0, B0, C0 lần lượt là cực của các cạnh BC, CA, AB thì A∗, B∗, C∗
chính là cực của các đường đối trung AA0, BB0, CC0.
iii) Vì AA0, BB0, CC0 đồng quy nên A∗, B∗, C∗ thẳng hàng, và đường thẳng
này còn gọi là trục Lemoine. Do đó trục Lemoine chính là đối cực của điểm
Lemoine . Trục Lemoine vuông góc với trục Brocard OL (trục Brocard là
đường thẳng O và điểm Lemoine L).
Bài toán 9. Cho tam giác ABC nội tiếp (O), T là điểm thuộc cạnh BC. Lúc
đó AT là đường đối trung khi và chỉ khi AT là trục đẳng phương của đường
tròn (O) và đường tròn A- Apolonius.
Chứng minh: Gọi D là giao điểm thứ hai của đường tròn A−Apollonius
và đường tròn (O), tức AD là trục đẳng phương của hai đường tròn. Gọi M là trung điểm của EF . [ BAC [ BAC Ta có \ M AB + = \ M AE = + [ ACB ⇒ \ M AB = [ ACB hay M A là 2 2
tiếp tuyến của (O) tại A.
Hơn nữa M A = M D, OA = OD nên M D đối xứng với M A qua OM , do đó
M D cũng là tiếp tuyến của (O) tại D.
Mà M thuộc BC nên tứ giác ABDC là tứ giác điều hòa, theo bài toán 7 ,
AD là đường đối trung của tam giác ABC 14 3 Bài tập vận dụng
Trong phần bài tập vận dụng là một số bài toán khai thác thêm một số
mô hình xuất hiện đường đối trung, tính chất của đường đối trung và một
số bài toán từ các cuộc thi học sinh giỏi được tiếp cận lời giải theo hướng
vận dụng các mối liên hệ giữa đường đối trung với các yếu tố trong hình học
phẳng nêu ở phần trên. Qua đó, ta có thể thấy được ý tưởng xây dựng các
bài toán từ các mối liên hệ giữa đường đối trung với các yếu tố hình học đã
phân tích ở trên. Ngoài ra, ta nhận thấy rằng lời giải sử dụng đường đối trung
cũng như các bổ đề nêu trên là lời giải khá ngắn gọn.
* Một số bài toán chứng minh đường đối trung
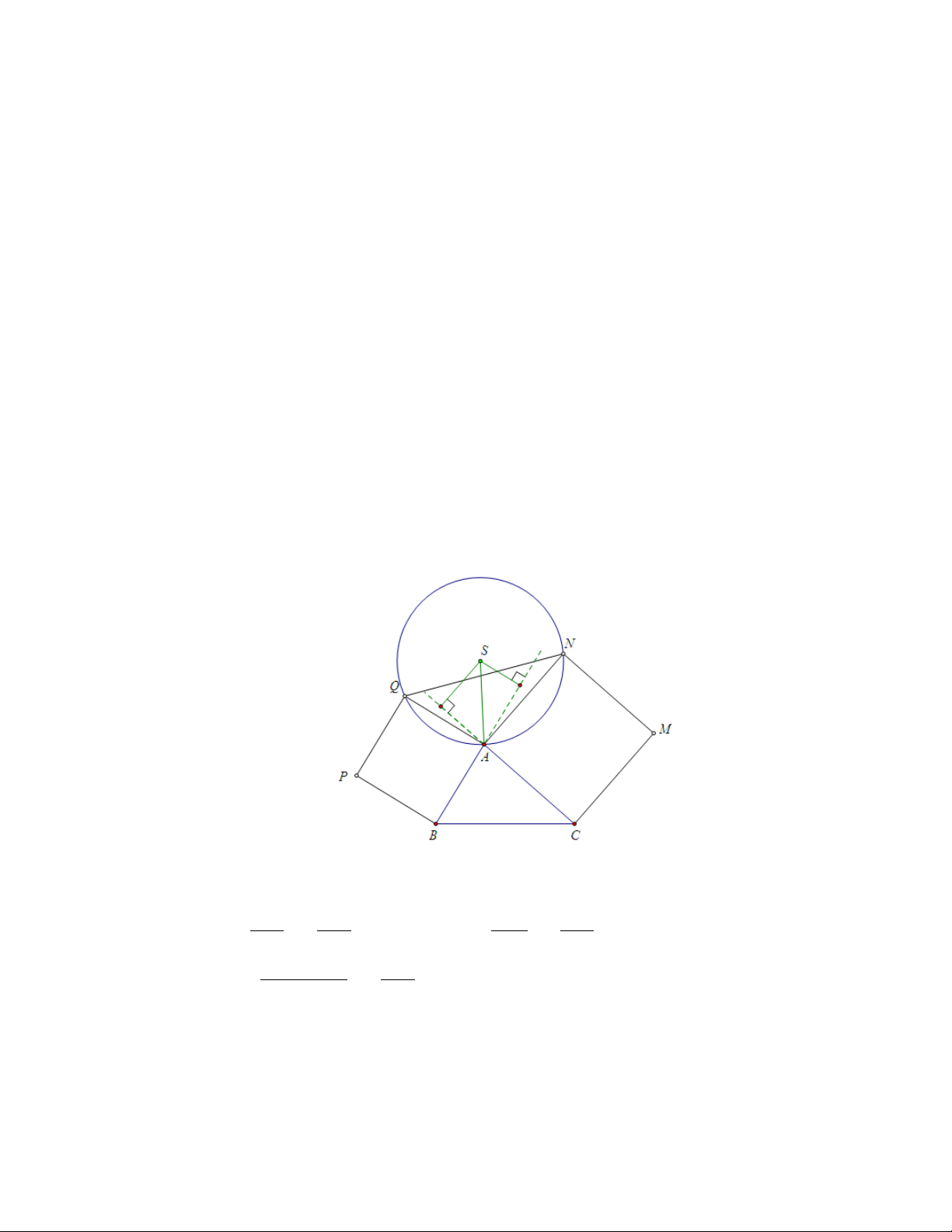
Bài 1. Cho tam giác ABC và ACM N, ABP Q là các hình vuông dựng ra
phía ngoài của tam giác. Gọi S là tâm của đường tròn ngoại tiếp tam giác
AN Q. Chứng minh rằng AS là đường đối trung của tam giác ABC. Lời giải:
Ta có S nằm trên đường trung trực của các đoạn thẳng AQ và AN , suy ra AQ AB AN AC d(S; AB) = = ; d(S; AC) = = . 2 2 2 2 d(S; AB) AB Từ đó suy ra =
hay AS là đường đối trung của tam giác ABC. d(S; AC) AC
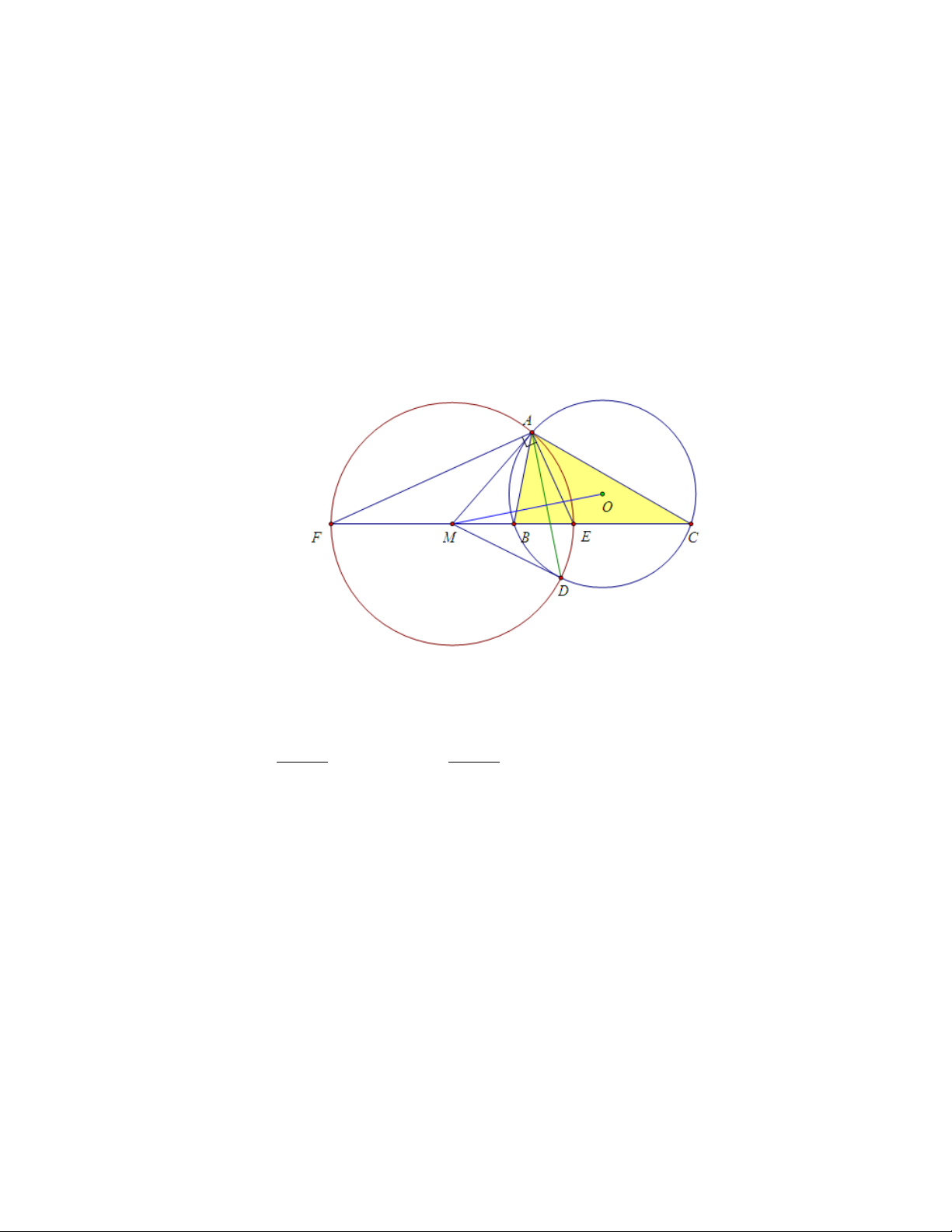
Bài 2. (Russia 2009-Grade 9) Cho tam giác ABC nội tiếp đường tròn
(O) có AD (D ∈ BC) là đường phân giác trong, đường thẳng AD cắt đường
tròn (O) tại điểm E khác điểm A. Đường tròn đường kính DE cắt (O) tại
điểm thứ hai là F . Chứng minh rằng AF là đường đối trung của tam giác ABC. 15 Lời giải:
Gọi M là trung điểm của BC. K là điểm đối xứng với E qua O. Ta có E, M, K thẳng hàng. Vì \ DF E = \
KF E = 900 nên K, D, F thẳng hàng. Do AKEF và
AKM D là các tứ giác nội tiếp nên [ EAF = \ EKF = \ M KD = \ M AD . Do
đó AF đối xứng với AM qua phân giác trong AD của góc [ BAC . Hay AF là đường đối trung.
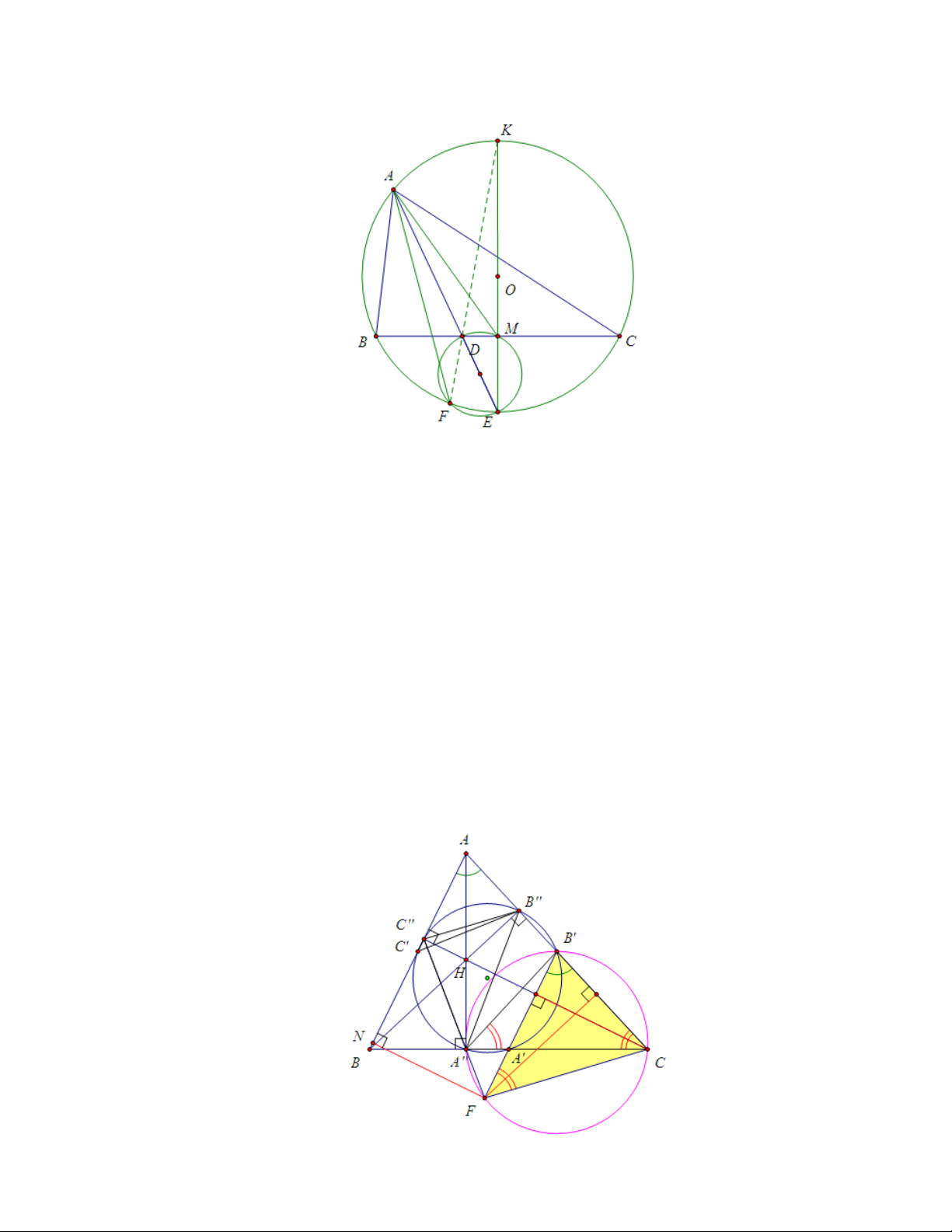
Bài 3. Cho tam giác ABC. A0, B0, C0 lần lượt là trung điểm của BC, CA, AB.
∆A00B00C00 là tam giác trực tâm (tức A00, B00, C00 lần lượt là chân các đường
cao kẻ từ A, B, C). Chứng minh rằng các đường thẳng A00, C00 và A0B0 giao
nhau tại điểm F nằm trên đường đối trung kẻ từ A của tam giác ABC.
Nhận xét Các điểm A0, B0, C0 , A00, B00, C00 làm xuất hiện đường tròn Ơle của tam giác ABC. Lời giải: 16
Dễ chứng minh các đường cao của tam giác ABC là các đường phân giác của tam giác A00B00C00 suy ra \ B00A00C = \ BA00C00 = \ F A00C (1)
Để ý rằng 6 điểm A0, B0, C0, A”, B”, C00 cùng thuộc đường tròn Euler của tam giác ABC, suy ra \ B00A00C = \ F B0C (2) Từ (1) và (2) suy ra \ F A00C = \
F B0C hay tứ giác AB0CF nội tiếp, ta được \ CF B0 = \ CA00B0 (3) . AC B0A00 = B0C =
nên ∆B0A00C cân tại B0, do đó \ CA00B0 = [ BAC (4). 2 Từ (3) và (4) suy ra \ CF B0 = [ BAC mà \ CB0F = [ CAB nên ∆CF B0 ∼ ∆BCA. Suy ra d(F ; AB) d(C; F B0) BB00 AB = = = . d(F ; AC) d(F ; AC) CC00 AC
Từ đó theo dấu hiệu 2 , ta được AF là đường đối trung.
* Về liên hệ giữa đường đối trung và đường đối song, đường song song với cạnh
Bài 4. Cho tam giác ABC, AE là đường đối trung (E thuộc cạnh BC), K
là điểm bất kỳ thuộc đoạn AE. Qua K kẻ các đường d1, d2 lần lượt đối song
với AB và AC. d1 cắt CA, CB lần lượt tại M, N . d2 cắt BA, BC lần lượt tại
P, Q. Chứng minh rằng M N = P Q. Lời giải:
Qua K kẻ B0C0 k BC, ta có AK là đường đối trung của tam giác AB0C0 nên
theo bài toán 2, ta được KM = KN . Mặt khác ta có \ M N C = [ BAC = \ P QB
nên tam giác KN Q cân tại K, suy ra KN = KQ. Vậy M N = P Q. 17
Bài 5. Cho tam giác ABC nội tiếp (O), AE là đường đối trung (E thuộc
cạnh BC), K là điểm bất kỳ thuộc đoạn AE. Qua K kẻ các đường d1, d2 lần
lượt song song với AB và AC. d1 cắt AC, CB tại I. d2 cắt AB tại J. Chứng minh rằng IJ ⊥AO. Lời giải:
Từ giả thiết ta suy ra AJ KI là hình bình hành, do đó AE đi qua trung điểm
của IJ , theo bài toán 1 ta được IJ là đường đối song của BC trong tam giác ABC.
Do đó IJ song song với tiếp tuyến tại A của đường tròn (O) hay IJ ⊥AO.
* Về liên hệ giữa đường đối trung và cực của cạnh
Bài 6. Cho tam giác ABC nội tiếp đường tròn (O) và có K là điểm Lemoine.
AK, BK, CK cắt lại (O) tương ứng ở D, E, F . Chứng minh rằng K cũng là
điểm Lemoine của tam giác DEF . Lời giải:
* Nếu tam giác ABC đều thì dễ suy ra kết quả.
* Nếu tam giác ABC vuông hoặc cân thì ý tưởng giải sau vẫn thực hiện được
bằng cách chọn đỉnh thích hợp. Cụ thể là giả sử tam giác đó vuông hoặc cân ở C .
Tiếp tuyến của (O) tại B và C cắt nhau ở P . Tiếp tuyến của (O) tại E và F
cắt nhau ở Q . Vì AK là đường đối trung của tam giác ABC nên A, K, D, T thẳng hàng.
Gọi J là giao điểm của EF và BC thì ta có S, D, K thẳng hàng vì cùng thuộc
đường đối cực của J đối với (O), do đó DA là đường đối trung của tam giác DEF .
Tương tự ta cũng chứng minh được EB là đường đối trung của tam giác DEF . 18
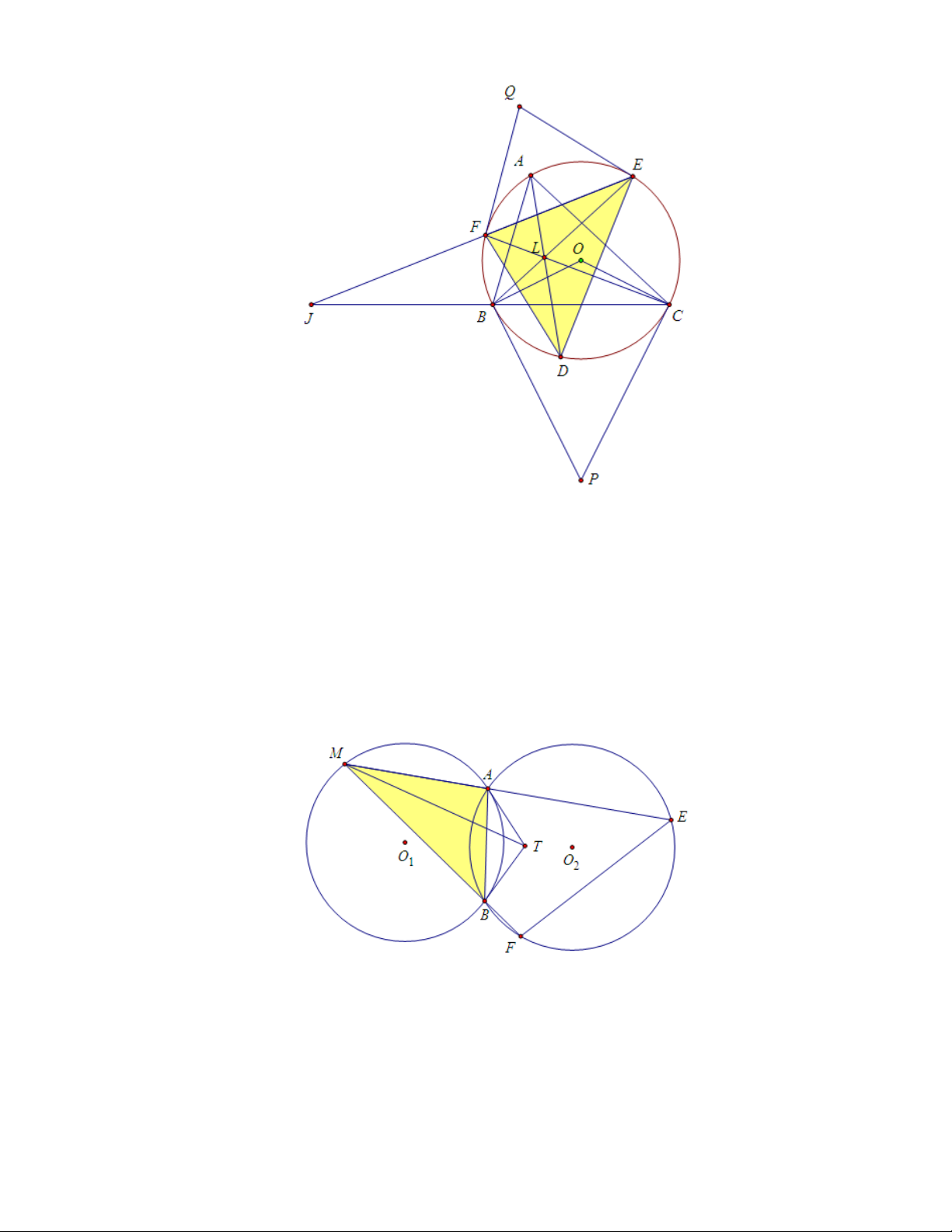
Bài 7. (St. Petersburg 1997 ) Cho hai đường tròn (O1), (O2) cắt nhau
tại hai điểm phân biệt A, B. Các tiếp tuyến của (O1) tại A và B cắt nhau tại
T . M là một điểm tùy ý của (O1) khác A, B và nằm ngoài đường tròn (O2).
Các đường thẳng M A, M B cắt đường tròn (O2) tại E, F . Chứng minh rằng
đường thẳng M T đi qua trung điểm của E, F . Lời giải:
Ta có T là đối cực của AB đối với (O1) nên M T là đường đối trung của tam giác M AB.
Mặt khác tứ giác ABF E nội tiếp nên EF đối song với AB trong tam giác M AB.
Vậy, M T đi qua trung điểm của EF . 19
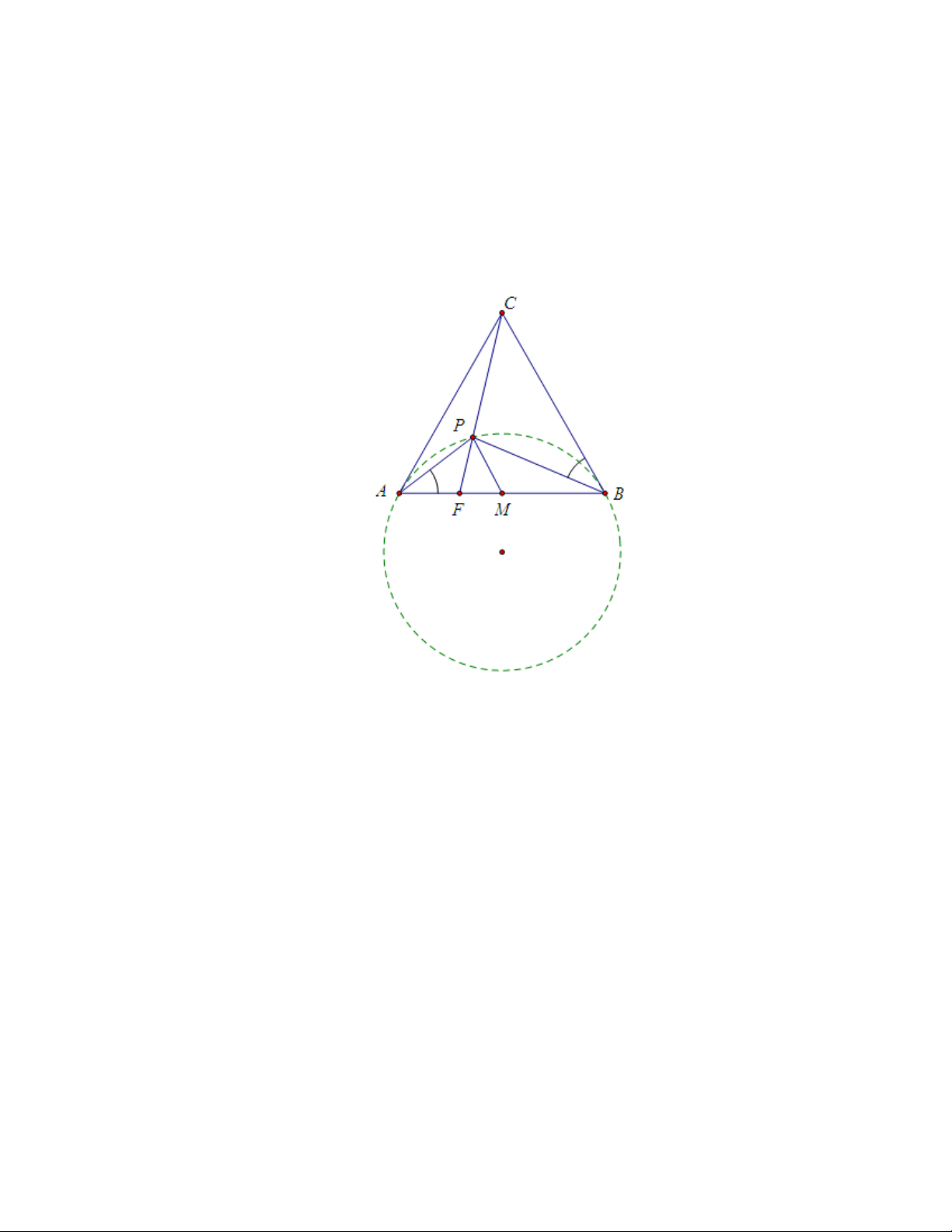
Bài 8. (Polan 2000) Cho tam giác ABC cân tại C. P là điểm nằm trong tam giác sao cho [ P AB = \
P BC. Gọi M trung điểm AB. Chứng minh \ CP B + \ AP M = 1800. Lời giải:
Vẽ đường tròn (O) ngoại tiếp tam giác P AB
Từ giả thiết ta có CB và AC là các tiếp tuyến của đường tròn (O).
Suy ra P C là đường đối trung của tam giác P AB, do đó CP đối xứng P M qua phân giác góc AP B.
Kéo dài CP cắt AB tại F, khi đó \ BP M = [ AP F Mà \ BP M + [ AP C = [ AP F + [ AP C = 1800 Suy ra \ CP B + \ AP M = 3600 − ( \ BP M + [ AP C) = 1800.
Bài 9. (Chọn đội tuyển PTNK 2010) Cho đường tròn (O) và điểm A
cố định trên (O), điểm B, C (khác điểm A) thay đổi trên (O) BC song song
với đường thẳng d cố định. Các tiếp tuyến của (O) tại B và C cắt nhau tại
K. Gọi M là trung điểm của BC, N là giao điểm của AM với (O). Chứng
minh đường thẳng KN luôn đi qua một điểm cố định khi BC thay đổi. Lời giải:
Gọi D, P lần lượt là giao điểm của KN, AK và (O). Vì BC có phương không 20