-
Thông tin
-
Quiz
Đường thẳng Simson, đường thẳng Steiner và điểm anti-Steiner | Toán 12
Cho tam giác ABC và một điểm P nằm trên đường tròn ngoại tiếp của nó. Khi đó các hình chiếu của P lên các cạnh AB, BC, CA nằm trên một đường thẳng, và đường thẳng đó gọi là đường thẳng Simson của điểm P đối với tam giác ABC. Tài liệu được sưu tầm giúp bạn tham khảo, ôn tập và đạt kết quả cao trong kì thi sắp tới. Mời bạn đọc đón xem!
Chương 3: Phương pháp tọa độ trong không gian 143 tài liệu
Toán 12 3.8 K tài liệu
Đường thẳng Simson, đường thẳng Steiner và điểm anti-Steiner | Toán 12
Cho tam giác ABC và một điểm P nằm trên đường tròn ngoại tiếp của nó. Khi đó các hình chiếu của P lên các cạnh AB, BC, CA nằm trên một đường thẳng, và đường thẳng đó gọi là đường thẳng Simson của điểm P đối với tam giác ABC. Tài liệu được sưu tầm giúp bạn tham khảo, ôn tập và đạt kết quả cao trong kì thi sắp tới. Mời bạn đọc đón xem!
Chủ đề: Chương 3: Phương pháp tọa độ trong không gian 143 tài liệu
Môn: Toán 12 3.8 K tài liệu
Thông tin:
Tác giả:
Preview text:
Đường thẳng Simson, đường thẳng Steiner và điểm anti-Steiner
Ong Thế Phương, khoá 2012-2013 THPT chuyên Lương Thế Vinh, Đồng Nai Ngày 1 tháng 11 năm 2012 1 Đường thẳng Simson: 1. Định nghĩa.
Cho tam giác ABC và một điểm P nằm trên đường tròn ngoại tiếp của nó. Khi đó các hình chiếu
của P lên các cạnh AB, BC, CA nằm trên một đường thẳng, và đường thẳng đó gọi là đường
thẳng Simson của điểm P đối với tam giác ABC. Chứng minh: A E D B C F P
Gọi D, E, F lần lượt là hình chiếu của P lên BC, CA, AB thì:
(DE, DP ) ≡ (CE, CP ) ≡ (CA, CP ) ≡ (BF, BP ) ≡ (DF, DP )(modπ). Do đó D, E, F thẳng hàng.
Chỉ dẫn lịch sử: Vào thế kỉ XIX, người ta cho rằng định lý này thuộc về nhà toán học người
Scotland là Robert Simson (1687-1768), và tên của ông được đặt cho định lý. Tuy nhiên bằng các
cuộc khảo sát và điều tra của J.S. Mackay thì định lý này ko nằm trong bất kì công trình nào của
Simson, và cũng ko có bất kì bằng chứng nào chứng tỏ định lý này thuộc về ông. Theo như Mackay
thì định lý này được khám phá lần đầu tiên bởi William Wallace, và nhiều nhà hình học bỏ qua
cái tên quen thuộc là đường thẳng Simson để gọi đường thẳng này mà thay vào đó là đường thẳng
Wallace. Hiện nay nó thường được gọi là đường Walace-Simson, và định lý trên được gọi là định lý Walace-Simson.
Trong bài viết này, cho gọn, ta sẽ ký hiệu SM (ABC) là đường thẳng Simson của tam giác ABC.
Chú ý rằng bài toán đảo lại của định lý Simson cũng đúng, cụ thể như sau: Cho tam giác ABC
và điểm P sao cho hình chiếu của nó xuống các cạnh của tam giác ABC nằm trên một đường
thẳng thì P nằm trên đường tròn ngoại tiếp tam giác ABC.
Chứng minh bài toán này đơn giản xin dành cho bạn đọc. 1 2. Một vài tính chất:
Trong mục này, chúng ta sẽ cùng đi đến những tính chất cơ bản nhất về đường thẳng Simson,
còn nhiều tính chất thú vị liên quan đến đường thẳng Simson sẽ được đề cập tới dưới dạng bài tập.
Với các kí hiệu như trên, ta thu được những tính chất sau:
Tính chất 1.1 Nếu Q là giao điểm của DP với đường tròn (ABC) thì ta có: AQkSM (ABC). Chứng minh:
(QA, QP ) ≡ (CA, CP ) ≡ (CE, CP ) ≡ (DP, DE)(modπ) ⇒ AQkSM (ABC)
Sau đây là một tính chất khá thú vị có liên quan đến đường thẳng Steiner sẽ được nói đến ở
phần sau, do đó trong phần này sẽ không nêu ra chứng minh.
Tính chất 1.2 Nếu H là trực tâm tam giác ABC thì đường thẳng SM (ABC) đi qua trung điểm HP .
Tính chất 1.3 Giao điểm của đường thẳng SM (ABC) với HP nằm trên đường tròn Euler của tam giác ABC. Chứng minh. A H O' E O D B M C F P
Gọi O và O0 lần lượt là tâm đường tròn ngoại tiếp và đường tròn Euler của tam giác ABC. M
là giao của SP (ABC) và P H. Khi đó theo tính chất 1.2 thì M là trung điểm P H. Mặt khác lại 1
có O0 là trung điểm của HO. Từ đó suy ra O0M =
OP . mà OP = R (bán kính của (O)), nên 2
suy ra M thuộc đường tròn Euler của tam giác ABC.
Tính chất 1.4 Q thuộc (O) sao cho AQ và AP là hai đường đẳng giác, khi đó AQ ⊥ SP (ABC)
Tính chất 1.5 P là một điểm bất kì trên đường trong (ABC) thì ta có: 1 −→ −→ π (SP (ABC), BC) ≡ OA, OP + (modπ) 2 2 Chứng minh: π 1 −→ −→ π
(SP (ABC), BC) ≡ (SP (ABC), P D) + (P D, BC) ≡ (CP, CA) + ≡ OA, OP + (modπ) 2 2 2
Tính chất 1.6 Gọi P và Q là hai điểm bất kì trên đường tròn (ABC) thì: −→ −→
(SP (ABC), SQ(ABC)) ≡ OP , OQ (modπ) Chứng minh: 2 A K Q P F H E B L G C
Gọi E, F là hình chiếu của P lên BC, BA; G, H là hình chiếu của Q lên BC, CA và K là
giao điểm của SP (ABC) và SQ(ABC); L là hình chiếu của K lên BC. Ta có:
(SP (ABC), SQ(ABC)) ≡ (KE, KG) ≡ (KE, KL) + (KL, KG) ≡ (EK, EP ) + (GQ, GK) ≡ −→ −→
(BA, BP ) + (CQ, CA)≡ OP , OQ (modπ).
Hệ quả 1. Nếu P và P 0 là hai điểm đối tâm đối với (O) thì SP (ABC) ⊥ SP 0(ABC).
Hệ quả 2. Với hai điểm khác nhau trên đường tròn ngoại tiếp tam giác ABC thì phương của
hai đường thẳng Simson của hai điểm đó cũng khác nhau.
Tính chất 1.7. Cho hai tam giác ABC và A’B’C’ cùng nội tiếp đường tròn (O) và P là một
điểm trên đường tròn đó, khi đó: 1 −→ −−→ 1 − − → −−→ 1 −→ −−→ (SP (ABC), SP (A0B0C0)) ≡ OA, OA0 + OB, OB0 + OC, OC0 (modπ) 2 2 2 Chứng minh:
Áp dụng Tính chất 1.4 ta có: 1 −→ −→
(SP (ABC), SP (A0B0C0)) ≡ (SP (ABC), BC)+(BC, B0C0)+(SP (A0B0C0)), B0C0) ≡ OA, OP + 2 1 −→ −−→ 1 −→ −−→ 1 − − → −−→ 1 −→ −−→ (BC, BC0) + (BC0, B0C0) + OP , OA0 ≡ OA, OA0 + OB, OB0 + OC, OC0 (modπ) 2 2 2 2
Hệ quả 1. Góc giữa hai đường thẳng Simson của P đối với tam giác ABC và A’B’C’ ko phụ
thuộc vào vị trí điểm M nằm trên đường tròn ABC.
Hệ quả 2. Chú ý rằng hai đường thẳng Simson vuông góc với nhau khi: −→ − −→ − − → −−→ −→ − −→ OA, OA0 + OB, OB0 + OC, OC0 ≡ π(modπ)
Hai đường thẳng Simson của M đối với tam giác ABC và A0B0C0 vuông góc với nhau nếu:
a) A0, B0, C0 là các điểm xuyên tâm đối của A, B, C.
b) A0 là điểm xuyên tâm đối của A và B0C0kBC. c) A0 trùng A và BC ⊥ B0C0
d) A0, B0, C0 là giao của các đường phân giác trong góc A, B, C của tam giác ABC với đường tròn (ABC)
e) A0, B0, C0 là giao của các đường cao đỉnh A, B, C của tam giác A, B, C với đường tròn (ABC)
Hệ quả 3. Tương tự thì ta cũng có hai đường thẳng Simson song song với nhau khi:
a) A0 là điểm xuyên tâm đối của A và B0C0 ⊥ BC. b) A0 trùng A và BCkB0C0.
c) A0, B0, C0 lần lượt là giao điểm của đường phân giác ngoài góc A, B, C của tam giác ABC với (ABC). 3
Tính chất 1.8 Cho tam giác ABC và A’B’C’ cùng nội tiếp 1 đường tròn, P và Q thuộc đường tròn đó thì ta có: 1 −→ −−→ 1 − − → −−→ 1 −→ −−→ 1 −→ −→ (SP (ABC), SQ(A0B0C0)) ≡ OA, OA0 + OB, OB0 + OC, OC0 + OQ, OP 2 2 2 2
Chứng minh điều này dựa vào các Tính chất 1.6 và Tính chất 1.7, xin dành cho bạn đọc. 2
Đường thẳng Steiner và điểm anti-Steiner: 1. Định nghĩa:
Định lý 1 (đường thẳng Steiner). Cho tam giác ABC và điểm P nằm trên đường tròn ngoại
tiếp tam giác đó. A0, B0, C0 là các điểm đối xứng với P qua BC, CA, AB. Khi đó ba điểm A, B,
C thẳng hàng và đường thẳng đi qua ba điểm này đi qua trực tâm H của tam giác ABC. Đường
thẳng đi qua A, B, C, H được gọi là đường thẳng Steiner của P đối với tam giác ABC. Chứng minh. A'' A B' A' H C' B C H' P
H0là giao điểm của AH với (ABC), A00 là giao điểm của P A0 với (ABC). Do A00AH0P là hình
thang cân và P H0 đối xứng với HA0 qua BC nên:
(A”A, A”P ) ≡ (P A”, P H0) ≡ (A0H, A0P )(modπ) Từ đó suy ra HA0kAA”(1).
Gọi D, E, F theo thứ tự là hình chiếu của P xuống BC, CA, AB. Như vậy D, E, F thẳng
hàng (đường thẳng Simson). Do đó A0, B0, C0 cũng thẳng hàng và đường thẳng qua A0, B0, C0 song
song với đường thẳng Simson của P đối với tam giác ABC và do đó song song với AA00 (Tính
chất 1.1). Từ đó và (1) ta có A0, B0, C0, H thẳng hàng.
Bây giờ ta sẽ đến với một định lý ngược lại của định lý 1 như sau:
Định lý 2 (định lý Collings hay điểm anti-Steiner) Cho tam giác ABC với trực tâm H.
Một đường thẳng d qua H. d1, d2, d3 là các đường thẳng đối xứng với d qua BC, CA, AB lần
lượt. Khi đó d1, d2, d3 đồng quy tại một điểm P nằm trên đường tròn ngoại tiếp tam giác ABC.
P được gọi là điểm anti-Steiner của d đối với tam giác ABC. Chứng minh: 4 A Hb N H B C Ha P
Gọi P là giao điểm của d1 và d2. AH và BH cắt (ABC) tại Ha, Hb. Như vậy d1, d2 lần lượt đi qua Ha, Hb.
Từ đó ta có: (AHa, d1) ≡ (d, AHa) ≡ (HbA, d2)(modπ). Do đó P thuộc (O).
Tương tự suy ra P 0 là giao điểm của d1 với d3 cũng thuộc (O) do đó d1, d2, d3 đồng quy tại một điểm thuộc (O).
Ghi chú: Từ Định lý 1 ta thấy rằng đường thẳng Steiner và đường thẳng Simson song song
với nhau và phép vị tự tâm P biến đường thẳng Simson thành đường thẳng Steiner theo số 2. Hơn
nữa đường thẳng Steiner đi qua H do đó đường thẳng Simson đi qua trung điểm của PH, và đây chính là Tính chất 1.2. 2. Một vài tính chất.
Như ta đã biết đường thẳng Simson và đường thẳng Steiner song song với nhau, do đó các
tính chất về góc của đường thẳng Simson và đường thẳng Steiner là như nhau nên ta sẽ ko nhắc
lại những tính chất này nữa. Cũng phải nói rằng, rất nhiều tính chất của đường thẳng Steiner và
điểm anti-Steiner có chứng minh phức tạp và phải dựa vào nhiều kết quả đã biết trước, nên dưới
đây ta chỉ đề cập đến một vài tính chất dễ chứng minh của đường thẳng Steiner, đồng thời cũng
là một số kết quả tiện cho việc tìm tòi và giải toán.
Tính chất 2.1 P thuộc đường tròn (ABC) thì đường thẳng Steiner và đường thẳng Simson
của P với tam giác ABC song song với nhau, và phép vị tự tâm P tỉ số 1 biến đường thẳng Simson 2
thành đường thẳng Steiner.
Tính chất 2.2. Kết hợp với Tính chất 1.1 ta có: nếu P là điểm anti-Steiner của d với tam
giác ABC. đường thẳng qua P vuông với BC cắt (ABC) lần nữa tại Q thì AQkd. 3 Một số ví dụ
Trong phần này ta sẽ sử dụng các tính chất của đường thẳng Simson, đường thẳng Steiner và điểm
anti-Steiner để giải các bài toán, đồng thời tìm hiểu thêm nhiều tính chất khác của chúng. 3.1
Các bài toán về quan hệ vuông góc và song song của các đường thẳng.
Các quan hệ vuông góc và song song là một trong những quan hệ cơ bản và có nhiều ứng dụng
nhất trong hình học phẳng, trong phần này, ta sẽ thấy được sức mạnh của các định lý đã nêu để
giải quyết các vấn đề về vuông góc và song song.
Ví dụ. (Chọn đội tuyển dự JBMO của Rumani, 2001) Cho tứ giác ABCD nội tiếp đường tròn
tâm (O) bán kính R. Với E là một điểm bất kì nằm trên (O), ta có K, L, M , N lần lượt là hình 5
chiếu của E trên AD, AB, BC, CD. Chứng minh rằng N là trực tâm của tam giác KLM khi và
chỉ khi ABCD là hình chữ nhật. Lời giải. L E Q A K M D B P N C
Cách 1. Dễ thấy rằng N là trực tâm của tam giác KLM khi và chỉ khi M N ⊥ LK và N K ⊥ M L.
Chú ý rằng M N , LK, N K, M L lần lượt là các đường thẳng Simson của E với các tam giác
BCD, ABD, ACD, BAC. Do đó theo Hệ quả 2 của Tính chất 1.7 ta có N là trực tâm tam giác KLM khi và chỉ khi: − − → −−→ (OB, OD) ≡ 0(modπ) −→ −→ (OA, OC) ≡ 0(modπ)
Từ đó suy ra N là trực tâm tam giác KLM khi và chỉ khi ABCD là hình chữ nhật.
Cách 2. Gọi P , Q lần lượt là hình chiếu của E lên BD, AC. Khi đó theo định lý Simson ta có
các cặp điểm thẳng hàng sau: (L, K, P ), (M, Q, L), (M, N, P ), (N, K, Q).
Gọi U , V là giao điểm của EP , EQ với (O), ta có U AkKL, U CkM N , V BkM L, V DkN K.
Do đó N là trực tâm tam giác KLM khi và chỉ khi:
M N ⊥ KLvà N K ⊥ M L ⇔ U A ⊥ U C và V B ⊥ V D ⇔ AC và BD là hai đường kính
⇔ ABCD là hình chữ nhật. 3.2
Các bài toán về đồng quy và thẳng hàng.
Ví dụ. (Điểm Parry reflection) Cho tam giác ABC. Qua A, B, C kẻ các đường thẳng α, β, γ song
song với đường thẳng Euler của tam giác. Gọi α0, β0, γ0 là các đường thẳng đối xứng với α, β, γ
qua BC, CA, AB. Khi đó α0, β0, γ0 đồng quy tại điểm Parry reflection của tam giác ABC. Lời giải. Cách 1. 6 A A' α H O α" B C Q α'
Gọi Q là điểm anti-Steiner của đường thẳng Euler đối với tam giác ABC. A0 là giao điểm
thứ 2 của α với (ABC), theo Tính chất 2.2 ta có QA0 vuông góc với BC. Hơn nữa chú ý rằng
OA0 = OQ nên OA0 đối xứng với OQ qua đường thẳng qua O song song với BC.
Suy ra đường thẳng đối xứng với OA0 qua BC song song với OQ. (1)
Gọi α” là đường thẳng đối xứng với đường thẳng Euler của tam giác ABC qua BC. Do phép −−→
tịnh tiến OA0 biến đường thẳng Euler thành đường thẳng α nên từ đó và (1) suy ra phép tịnh tiến −→ OQ biến α” thành α0.
Tương tự gọi β”, γ” là đường thẳng đối xứng với đường thẳng Euler qua AC và AB lần lượt −→
thì phép tịnh tiến OQ biến β” thành β0, biến γ” thành γ0. Hơn nữa theo định lý Collings thì α”,
β”, γ” đồng quy, vậy suy ra α0, β0, γ0 đồng quy. Cách 2. A1 A H O B D E C B1 F C1 A2
Gọi A1, B1, C1 là ba điểm đối xứng của O lần lượt qua A, B, C. Suy ra phép vị tự tâm O, tỉ
số 2 biến tam giác ABC thành A1B1C1. Do đó hai đường thẳng Euler của hai tam giác ABC và A1B1C1 trùng nhau.
Gọi A2 là điểm đối xứng của A qua BC. Suy ra A2 thuộc α0. Ta sẽ chứng minh rằng α0 đối
xứng với đường thẳng Euler của tam giác A1B1C1 qua B1C1. 7
Gọi D, F là giao điểm của AA2 với BC và B1C1. Ta có:
HA2 = AA2−AH = 2 AD − OE = 2 AH + HD − OE = 2 OE + HD = 2 DF + HD = 2HF
Từ đó suy ra α0 đối xứng với đường thẳng Euler của tam giác A0B0C0 qua B0C0, tương tự β, γ
đối xứng với đường thẳng Euler của tam giác A0B0C0 qua CA, AB lần lượt. Từ đó theo định lý
Collings thì α0, β0, γ0 đồng quy.
Ví dụ. (Đường thẳng Droz-Farny) Cho hai đường thẳng bất kì vuông góc với nhau tại trực
tâm tam giác ABC. Chúng tương ứng cắt các cạnh BC, CA, AB tại X, X0, Y , Y 0, Z, Z0. Khi đó
ta có Ma, Mb, Mc tương ứng là trung điểm XX0, Y Y 0, ZZ0 thẳng hàng. Lời giải. Y' A Hb Z' Y Hc H Z X X' C B Ha P
Gọi Ha, Hb, Hc lần lượt là điểm đối xứng với H qua BC, CA, AB.
Suy ra Ha, Hb, Hc đều thuộc (ABC), và ta có ∠XHaX0 = ∠CHX, ∠Y HbY 0 = ∠Y HY 0,
∠ZHZ0 = ∠ZHcZ0. Từ đó suy ra Ha, Hb, Hc lần lượt thuộc đường tròn đường kính XX0, Y Y 0, ZZ0.
Mặt khác theo định lý Collings ta có XHa, Y Hb, ZHc đồng quy tại một điểm P thuộc (ABC).
Và do đó áp dụng định lý Miquel vào tam giác P Y Z có H ∈ Y Z, Hc ∈ ZP , Hb ∈ Y P . Ta có
(P HbHc), (ZHHc), (Y HHb) đồng quy. Do đó đường tròn (ABC), đường tròn đường kính ZZ0 và Y Y 0 đồng quy.
Tương tụ đường tròn (ABC), đường tròn đường kính XX0, Y Y 0 đồng quy, đường tròn (ABC),
đường tròn đường kính XX0, ZZ0 đồng quy.
Từ đó suy ra đường tròn đường kính XX0, Y Y 0, ZZ0 đồng quy tại một điểm khác H. Do đó
tâm của chúng thẳng hàng. Hay Ma, Mb, Mc thẳng hàng.
Để kết thúc phần này, ta sẽ đến với bài toán sau, bài toán sau đây là một bài toán không phải
quá khó với nhiều bạn học sinh, tuy vậy nó là một bài toán khá hay, chúng ta sẽ cùng gặp lại nó sau
phần Ứng dụng của đường thẳng Simson, đường thẳng Steiner, và điểm anti-Steiner này.
Ví dụ. Cho tứ giác ABCD nội tiếp đường tròn (O). Gọi Sa, Sb, Sc, Sd lần lượt là các đường
thẳng Simson của A với tam giác BCD, B với tam giác ACD, C với tam giác ABD, và D với
tam giác ABC. Chứng minh rằng Sa, Sb, Sc, Sd đồng quy. Chứng minh. 8 B O A H H c d I C D
Gọi Ha, Hb, Hc, Hd lần lượt là trực tâm của tam giác BCD, ACD, ABD, ABC. M là trung điểm AB. Do đó DHc = 2OM = CHd.
Mặt khác DHckCHd nên tứ giác DCHdHc là hình bình hành. Từ đó DHd, CHc cắt nhau tại trung điểm mỗi đường.
Tương tự ta thu được AHa, BHb, CHc, DHd cắt nhau tại trung điểm mỗi đường.
Chú ý rằng ta có Sa đi qua trung điểm AHa, Sb đi qua trung điểm BHb, Sc đi qua trung điểm
CHc, Sd đi qua trung điểm DHd, nên ta có Sa, Sb, Sc, Sd đồng quy tại trung điểm của AHa, BHb, CHc, DHd. 3.3
Các bài toán về đồng viên
Đồng viên là một trong những vấn đề rộng lớn trong hình học phẳng, có rất nhiều định lý và bài
toán nổi tiếng liên quan đến khái niệm đồng viên, trong mục này, ta sẽ khám phá ứng dụng của
đường thẳng Simson, đường thẳng Steiner và điểm anti-Steiner để giải quyết các vấn đề liên quan
đến đồng viên. Trước tiên là một định lý hết sức quen thuộc và vô cùng quan trọng trong hình học phẳng: Ví dụ
a) (Điểm Miquel) Cho tứ giác toàn phần ABCDEF . Khi đó các đường tròn ngoại tiếp các tam
giác AEF , DCE, ABC, BDF đồng quy tại 1 điểm, điểm đó gọi là điểm Miquel của tứ giác toàn phần.
b) (Đường tròn Miquel) Cho tứ giác toàn phần ABCDEF . Khi đó điểm Miquel và tâm ngoại
tiếp các tam giác AEF , CDE, ABC, BDF cũng nằm trên đường tròn, đường tròn đó gọi là đường
tròn Miquel của tứ giác toàn phần. Lời giải. a) 9 A M F E B C D
Gọi M là giao điểm của (ABC) và (AEF ). Ta có:
(F M, F E) ≡ (AM, AC) ≡ (BM, BC) ≡ (BM, BD)(modπ)
Suy ra F , M , D, B đồng viên.
Tương tự thì C, E, M , D đồng viên. Từ đó suy ra các đường tròn AEF , DCE, ABC, BDF đồng quy tại 1 điểm. b) A M R Oa F S Oc T O E B O C D b
Gọi O, Oa, Ob, Oc là tâm đường tròn ngoại tiếp các tam giác ABC, AEF , BDF , CED.
R, S, T là trung điểm của M A, M E, M C lần lượt. Ta có M A ⊥ OOa, M C ⊥ OOc, M E ⊥ OaOc.
Hơn nữa dễ thấy R, S, T thẳng hàng, do đó theo định lý đảo lại của đường thẳng Simson ta
có M , O, Oa, Oc đồng viên.
Tương tự M , Oa, O, Ob đồng viên.
Do đó M , O, Oa, Ob, Oc đồng viên.
Trên đây là định lý Miquel, một định lý rất quan trọng trong hình học, tiếp đến ta sẽ đến với
một vài tính chất có liên quan đến đường thẳng Steiner mà theo tác giả thì nó rất hay và đẹp.
Ví dụ. Cho tam giác ABC nội tiếp đường tròn (O). P là một điểm bất kì trong mặt phẳng.
Gọi A1, A2, A3 lần lượt là giao điểm của AP , BP , CP với đường tròn (O). A2, B2, C2 lần lượt là
các điểm đối xứng của (O) qua BC, CA, AB. Chứng minh rằng 4 đường tròn (ABC), (P A1A2),
(P B1B2), (P C1C2) đồng quy. Lời giải. 10 A P A2 H B C Ha Q A1 A3
Gọi A3 là điểm đối xứng của P qua BC. Khi đó rõ ràng ta có P , A3, A1, A2 đồng viên.
Gọi Q là điểm anti-Steiner của đường thẳng HP với tam giác ABC (trong đó H là trực tâm
tam giác ABC) thì Q thuộc (ABC). Ta sẽ chứng minh Q cũng thuộc các đường tròn (P A1A2), (P B1B2), và (P C1C2).
Halà giao điểm của AH với (O), như vậy HaA3 đối xứng với HP qua BC, nên theo định lý
Collings HaA3 đi qua Q. Mặt khác lại có HHaQP là hình thang cân nên:
(A3Q, A3P ) ≡ (HaQ, HaA) ≡ (A1Q, A1A)(modπ)
Từ đó suy ra Q, A3, P , A1 đồng viên, do đó P A1A2 đi qua Q.
Chứng minh tương tự thì P C1C2 và P B1B2 cũng đi qua Q. Từ đó ta thu được kết luận của bài toán.
Ta cùng đi đến một bài toán nữa của tác giả Nguyễn Văn Linh cùng với hai lời giải, lời giải
của tác giả bài toán tuy dài hơn nhưng cũng chứa đựng nhiều điều thú vị, đáng học hỏi.
Ví dụ.(Nguyễn Văn Linh, mathley round 2) Cho tam giác ABC nội tiếp đường tròn (O)
với trực tâm H. Một đường thẳng đi qua H cắt đường tròn (O) tại hai điểm P và Q. Qua P , Q
lần lượt kẻ các đường vuông góc với AP và AQ, các đường này cắt BC lần lượt tại M , N . Chứng
minh rằng đường thẳng qua P và vuông góc với OM và đường thẳng qua Q và vuông góc với ON
cắt nhau tại một điểm nằm trên đường tròn (O)
Lời giải 1. (Lê Bích Ngọc, học sinh chuyên toán chuyên KHTN) 11 A Q H O P M Z B C Y N X S T
Gọi đường thẳng qua P và vuông góc với OM và đường thẳng qua Q và vuông góc với ON cắt
nhau tại T . Gọi AS là đường kính của (O). Gọi X, Y , Z là hình chiếu của (O) lên P S, BC, SQ. −−→ 1 −→ − − → 1 − −→ −→ 1 −→ Dễ thấy OX = AP , OY = AH, OZ =
AQ. Mà P , Q, H thẳng hàng suy ra X, Y , Z 2 2 2 thẳng hàng.
Theo bài toán đảo của đường thẳng Simson suy ra O, M , N , S đồng viên, từ đó ta có biến đổi góc sau đây:
(T P, T Q) ≡ (OM, ON ) ≡ (SM, SN ) ≡ (SP, SQ)(modπ)
Từ đó S, T , P , Q đồng viên hay T thuộc (O).
Lời giải 2 (Nguyễn Văn Linh)
Lời giải này thông qua bổ đề sau:
Bổ đề: Cho tam giác ABC nội tiếp đường tròn tâm (O) với trực tâm H. Một đường thẳng
bất kì qua O cắt AB, AC tại I, J . Khi đó:
a) Các đường tròn đường kính BI và CJ cắt nhau tại một điểm F nằm trên (O).
b) Gọi G là điểm đối xứng của F qua IJ thì G thuộc (O), khi đó HF là đường thẳng Steiner
của G đối với tam giác ABC. Chứng minh bổ đề. 12 L A M G H K P I O J C B F
a) Kẻ đường kính CP và BK của (O). Áp dụng định lý Pascal đảo cho 6 điểm A, B, C, P ,
F , K ta suy ra P J và IK giao nhau tại một điểm F thuộc (O). Vì CP và BK là đường kính của
(O) nên ta cũng dễ thấy F thuộc các đường tròn đường kính BI và CJ (đpcm).
b) Gọi L là giao của BH với (O), M là giao của GL và AC. Do BH, BO là hai đường đẳng
giác trong góc ∠BAC nên LKkAC do đó ta có: 1 −→ −→ − → −→ 1 −→ −→ −→ − −→ (M G, M I) ≡ (M G, M A) ≡ OG, OA + OL, OC ≡ OG, OA + OA, OK ≡ 2 2 1 −→ −−→ OG, OK
≡ (F G, F K) ≡ (F G, F I)(modπ). 2
Do đó tứ giác GM IF nội tiếp, suy ra (M F, M I) ≡ (GF, GI) ≡ (F I, F G) ≡ (M I, M G)(modπ).
Suy ra M F , M G đối xứng nhau qua AC kéo theo điểm đối xứng với G qua AC nằm trên M F .
Mặt khác dễ thấy H, L đối xứng với nhau qua AC và L thuộc M G do đó H thuộc M F . Vậy
HF là đường thẳng Steiner của G đối với tam giác ABC. Đó là điều phải chứng minh. Trở lại bài toán. A P H J O N B M C Q
Áp dụng bổ đề trên ta suy ra giao điểm J của (O) và đường thẳng qua P vuông góc với OM
là điểm anti-Steiner của đường thẳng P H trong tam giác ABC. Tương tự giao điểm J 0 của (O)
và đường thẳng qua Q vuông góc với ON là điểm anti-Steiner của đường thẳng QH trong tam
giác ABC. Vậy J ≡ J 0. Ta có kết luận của bài toán. 13 3.4
Các bài toán về điểm và đường cố định.
Trước hết chúng ta cũng xem qua ví dụ đơn giản sau:
Ví dụ. Cho hai đường tròn (O1) và (O2) cắt nhau tại A, B. Một cát tuyến thay đổi qua A cắt
(O1) tại C và (O2) tại D. Tiếp tuyến tại C của (O1) và tiếp tuyến tại D của (O2) cắt nhau tại P .
Gọi H, K là hình chiếu của B lên P C và P D. Chứng minh HK luôn tiếp xúc với đường tròn cố định. Lời giải: P H C A D J I K B
Rõ ràng bài toán có ý nhắc chúng ta nghĩ đến đường thẳng Simson, chúng ta cùng xem lời giải sau:
Gọi I là trung điểm AB còn J là hình chiếu của B lên CD.
Ta có: (BC, BD) ≡ (BC, BA)+(BA, BD) ≡ (CP, CA)+(DA, DP ) ≡ (CP, CD)+(CD, DP ) ≡ (CP, DP )(modπ)
Từ đó suy ra P, C, B, D đồng viên, do đó H, J, K thẳng hàng. Hơn nữa lại có:
(IJ, HK) ≡ (IJ, J B) + (J B, HK) ≡ (J B, AB) + (J B, J K) ≡ (BK, BD) + (J B, J K) ≡ π
(J K, J D) + (J B, J K) ≡ (J B, ID) ≡ (modπ) 2
Từ đó suy ra IJ ⊥ HK ⇒ HK tiếp xúc với đường tròn đường kính AB. Do đó HK tiếp xúc
với đường tròn cố định
Bài toán trên là ví dụ khá cơ bản về đường thẳng Simson trong việc tìm các yếu tố cố định,
sau đây cũng là một ví dụ về các yếu tố cố định liên quan đến hai đường thẳng Simson.
Ví dụ. Cho tam giác ABC nội tiếp đường tròn (O), P và Q là hai điểm xuyên tâm đối với
nhau qua (O). Chứng minh rằng giao điểm hai đường thẳng Simson của P và Q với tam giác ABC
thuộc một đường cố định. Lời giải: 14 F' Q A M' E' H O' E O D B C D' M F P
Gọi D, E, F là hình chiếu của P lên BC, CA, AB và D0, E0, F 0 là hình chiếu của Q lên BC,
CA, AB. Do đó theo định lý về đường thẳng Simson ta có D, E, F thẳng hàng và D0, E0, F 0 thẳng hàng.
Gọi H và trực tâm tam giác ABC và O0 là tâm đường tròn Euler của tam giác ABC, M và
M 0 lần lượt là giao điểm của đường thẳng qua D, E, F với HP và đường thẳng qua D0, E0, F 0 với
HQ. Khi đó theo Tính chất 1.4 thì ta có M và M 0 lần lượt là trung điểm của P H và QH.
Mặt khác ta lại có O0 là trung điểm của HO, do đó ta suy ra được M , O, O0 thẳng hàng, từ đó R
chú ý rằng M M 0 là đường trung bình của tam giác HP Q như vậy O0M 0 = O0M = hay M và 2
M 0 thuộc đường tròn Euler của tam giác ABC đồng thời vì M M 0 = R nên M M 0 cũng là đường
kính của đường tròn Euler của tam giác ABC.
Từ đó theo hệ quả 1 của tính chất 1.6 thì ta được hai đường thẳng qua D, E, F và D0, E0, F 0
vuông góc với nhau, do vậy giao điểm của chúng nằm trên đường tròn Euler của tam giác ABC
(cố định), ta hoàn thành chứng minh.
Trên đây là một ví dụ khá thú vị, nó giúp ta thấy được mối liên hệ giữa đường thẳng Euler
của tam giác và hai đường thẳng Simson của hai điểm xuyên tâm đối đối với tam giác đó tiếp tục
mối liên hệ giữa các đường thẳng Simson và đường tròn Euler ta sẽ tìm hiểu tiếp ở phần Các vấn
đề liên quan đến đường tròn Euler ở phần sau, đối với để tiếp tục phần này, mời bạn đọc đến
với một ví dụ khá đẹp mắt sau, ví dụ dưới đây cần sự phán đoán hợp lý để tìm yếu tố cố định:
Ví dụ. Cho tam giác ABC, M là một điểm thay đổi trên BC. Gọi D, E là điểm đối xứng của
M qua AB, AC. Chứng minh trung điểm DE thuộc một đường thẳng cố định khi M thay đổi trên BC. Lời giải: 15 A B' P D N C' Q R E H B C M
Không như các ví dụ trên, ví dụ này, không nhắc chúng ta nghĩ đến đường thẳng Simson, hay
đường thẳng Steiner, tuy nhiên ta vẫn có thể dùng phán đoán để giải bài này như sau.
Suy nghĩ một chút, ta sẽ thấy khi M di chuyển trên BC thì nó đi qua hai điểm đặc biệt rất
dễ nhìn thấy, đó là B và C, hơn nữa, khi đó trung điểm DE sẽ lần lượt trùng với chân đường cao
hạ từ B và C xuống các cạnh tương ứng, đến đây, ý tưởng của ta là chứng minh trung điểm DE,
chân các đường cao từ B và C thẳng hàng, ta đi đến lời giải sau:
Gọi H là trực tâm tam giác ABC. P và Q lần lượt là giao điểm của CH và BH với DE, R là
giao điểm thứ hai của đường tròn (ADM ) với AC.
Từ đó ta có: (RC, RE) ≡ (RM, RC) ≡ (DM, DA) ≡ (M A, M D) ≡ (RA, RD)(modπ)
Từ đó suy raD, R, E thẳng hàng. Do đó (AC, AE) ≡ (AM, AC) ≡ (AM, AR) ≡ (DM, DR) ≡ (P C, P E)(modπ)
Suy ra A, E, C, P đồng viên.
Nên (P A, P Q) ≡ (P A, P E) ≡ (CA, CE) ≡ (CM, CA) ≡ (HA, HQ)(modπ)
Như vậy A, P, Q, H đồng viên.
Gọi C0, B0 lần lượt là chân các đường cao đỉnh B, C của tam giác ABC. N là trung điểm của DE
Ta có AD = AM = AE do đó AN ⊥ DE, hơn nữa AC0 ⊥ P H, AB0 ⊥ QH. Như vậy theo
định lý Simson thì N , B0, C0 thẳng hàng. Suy ra N nằm trên B0C0 cố định.
Ví dụ sau đây đòi hỏi chúng ta phải phán đoán các yếu tố cố định ở mức độ cao hơn:
Ví dụ. Cho tứ giác ABCD khác hình thang có AD = BC, trên hai cạnh AD và BC lấy E, F
sao cho DE = BF . Gọi P là giao điểm của AC và BD, đường thẳng EF cắt AC và BD tại Q và
R. Chứng minh rằng đường tròn ngoại tiếp tam giác P QR đi qua một điểm cố định khác P khi E, F thay đổi. Lời giải. D E J S A R P K I Q B F C 16
Gọi I, J , K lần lượt là trung điểm của AC, BD, EF .
S là giao điểm của đường trung trực DB và AC. Do đó SB = SD; SA = SC nên ∆SAD = ∆SCB
Từ đó suy ra SE = SF hay SK là trung trực của EF . ED BF Đặt k = = EA CF −→ −→ −→ − −→ − − → −→
Ta có: 2KI = EA + F C = k DE + BF = 2kJ K
Từ đó suy ra I, J , K thẳng hàng.
Chú ý rằng I, J , K lần lượt là hình chiếu của S lên AC, BD, EF và I, J , K thẳng hàng nên
S nằm trên đường tròn (P QR). Hơn nữa S cố định, do đó (P QR) đi qua S cố định.
Nhận xét: Chắc hẳn nhiều bạn đọc sẽ cho rằng ví dụ trên đây có cách giải rất không tự nhiên,
đúng là vậy, thoạt nhìn thì nó không tự nhiên, nhưng thông qua bổ đề nổi tiếng sau đây, bạn sẽ
thấy rằng, cách giải trên là hợp lý và rất tự nhiên.
“Bổ đề E.R.I.Q. Cho hai bộ ba điểm thẳng hàng (A1, A2, A3) và (B1, B2, B3) thỏa A1A2 B C = 1B2 = k 1A1
. Trên A1B1, A2B2, A3B3 lần lượt lấy C1, C2, C3 thỏa thỏa = A1A3 B1B3 C1B1 C2A2 C = 3A3 . C2B2 C3B3 C1C2
Khi đó C1, C2, C3 thẳng haàng và = k” C1C3
Từ bổ đề E.R.I.Q này và chú ý rằng bài toán của chúng ta yêu cầu chứng minh đường tròn
đi qua điểm cố định, do đó ý tưởng của chúng ta sẽ là tìm ba điểm I, J , K đủ đặc biệt trên các
cạnh của tam giác P , Q, R sao cho I, J , K thẳng hàng (và điều này bổ đề E.R.I.Q đã giúp ích
ta rất nhiều), hơn nữa nó phải đủ đặc biệt để có thể dễ dàng tìm ra điểm S có hình chiếu lên các
cạnh của tam giác P QR chính là các điểm I, J , K. Và vì trung điểm đoạn thẳng là các điểm đặc
biệt hơn cả nên việc lựa chọn trung điểm để giải bài này qua đó cũng không mấy khó khăn.
Tuy nhiên, đối với bài toán trên đây thì việc tìm điểm cố định bằng bổ đề E.R.I.Q thì tương
đối thuận tiện, hơn nữa nó có ý tưởng cho ta xây dựng bài toán tổng quát sau:
Bài toán (Ong Thế Phương) Cho một tứ giác lồi ABCD, trên AC và BD lấy các điểm E, AE DF F sao cho =
. Gọi P là giao điểm của CE và DA, Q và R là giao điểm của EF với CE AC DE
và AD. Chứng minh đường tròn ngoại tiếp tam giác P QR luôn đi qua một điểm cố định khi E, F thay đổi trên AC và BD. 3.5 Một số bài toán khác
Ví dụ. Cho tam giác ABC nội tiếp đường tròn (O), gọi M là điểm nằm trên cung nhỏ BC, gọi
H; K; I lần lượt là hình chiếu của M xuống BC và AB, AC. Kẻ M N vuông góc với tiếp tuyến
Bx của (O) tại B. Chứng minh rằng:M H.M K = M I.M N Lời giải. 17 A O I H B C K M N
Do góc ∠M N B = ∠M HB = ∠M KB = 900 nên rõ ràng ta có H, B, K, N , M đồng viên, từ
đó ta thu được: (HM, HI) ≡ (N M, N K)(modπ)
Hơn nữa lại có: (N M, N K) ≡ (BM, BK) ≡ (CM, CA) ≡ (HM, HI)(modπ) M N M K
Do đó ∆M N K ∼ ∆M HI suy ra: = hay M H.M K = M N.M I M H M I
Ví dụ. (IMO 2007) Xét 5 điểm A, B, C, D, E sao cho ABCD là hình bình hành và B, C, D,
E cũng thuộc một đường tròn. Gọi d là một đường thẳng qua A. Giả sử d cắt đoạn DC ở F và
BC ở G. Giả sử EF = EG = EC, chứng minh rằng d là phân giác ∠DAB. Lời giải. G M E C N B F P D A
Gọi M, N lần lượt là hình chiếu của E lên BC, CD. P là trung điểm CA.
Do EC = EF = EG nên E là tâm đường tròn ngoại tiếp tam giác CF G và do đó M và N
là trung điểm của CG và CF . Do đó M N song song với d, do đó M , N , P thẳng hàng, nên theo
định lý về đường thẳng Simson ta có P là hình chiếu của E lên BD.
Mặt khác Do P là trung điểm CA nên N P cũng song song với d mà do ABCD là hình bình
hành nên P là trung điểm BD.
Như vậy E là điểm chính giữa cung BD. Do đó ∆ECM = ∆ECN nên CM = CN hay CG = CF .
Từ đó dễ dàng suy ra d là phân giác của ∠DAB.
Trên đây chỉ là những ứng dụng nhỏ của đường thẳng Simson và đường thẳng Steiner, thật ra
còn rất nhiều tính chất khác rất hay và đẹp liên quan đến các vấn đề này, do khuôn khổ bài viết 18
có hạn nên tác giả xin dừng lại bài viết này. Kết thúc bài viết, xin dành cho các bạn một số bài tập để rèn luyện.
Bài 1. Cho đường tròn (O) và đường thẳng d không cắt nó.Điểm M thay đổi trên d, kẻ các
tiếp tuyến M T, M H với (O).Gọi A là hình chiếu vuông góc của O lên d và E, F lần lượt là hình
chiếu vuông góc của A lên M T, M H.Chứng minh rằng:
a)Đường thẳng T H đi qua một điểm cố định.
b)Đường thẳng EF đi qua một điểm cố định.
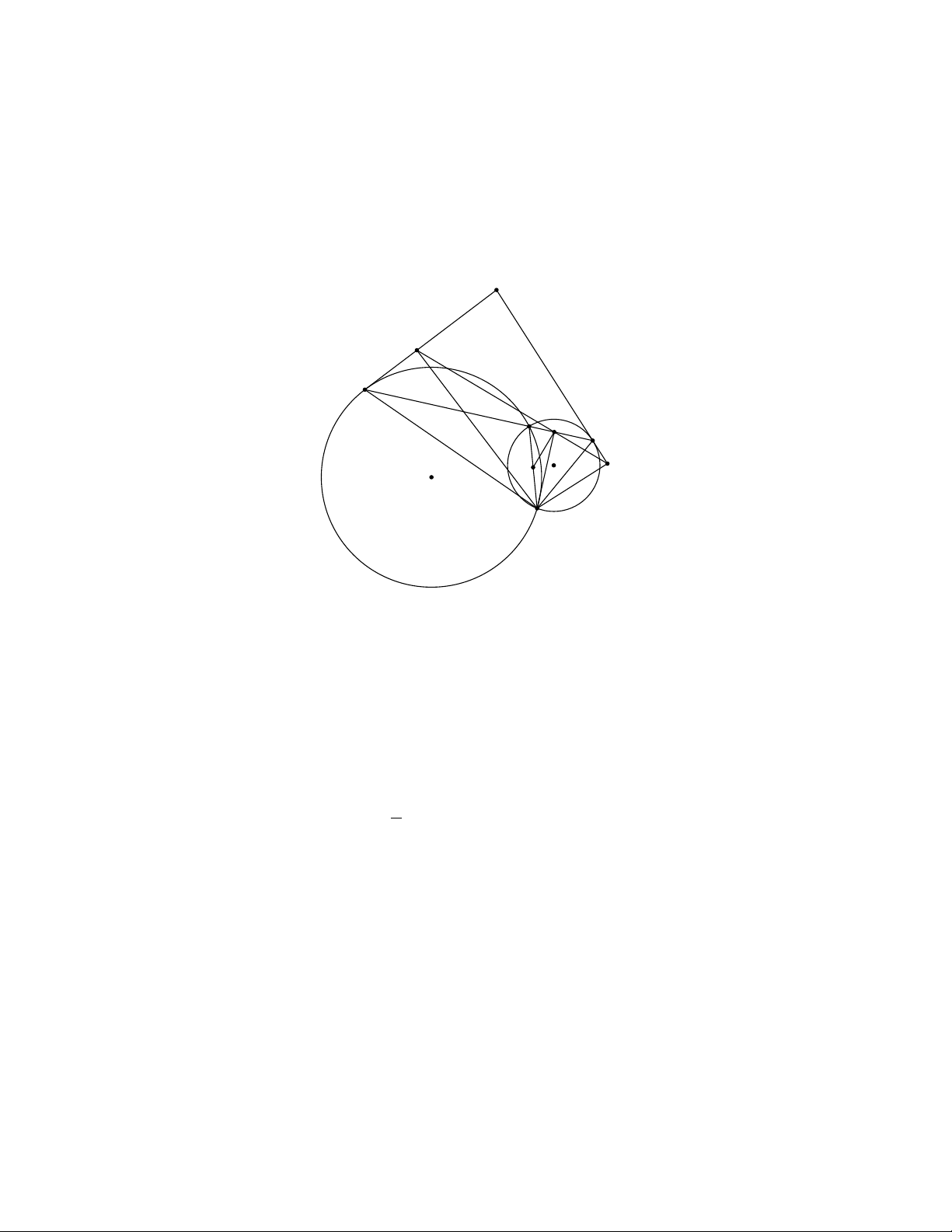
Bài 2. Cho tam giác ABC, K và J lần lượt là tâm đường tròn bàng tiếp góc C và góc B của
tam giác. P , Q, R, S lần lượt là hình chiếu của A lên KB, KC, BJ , CJ . Gọi B0, C0 là trung điểm
AB, AC. Chứng minh rằng P , Q, R, S, B0, C0 thẳng hàng.
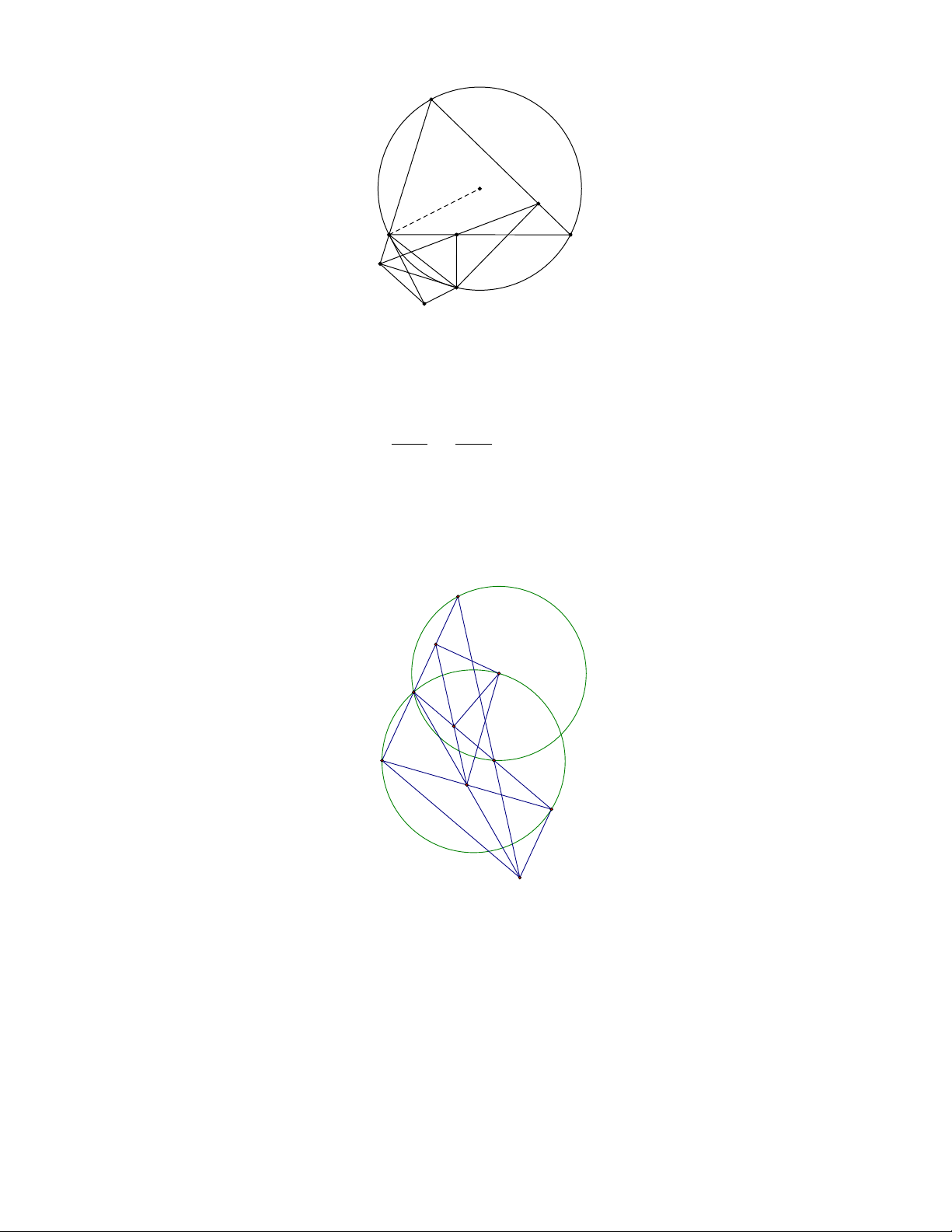
Bài 3. Cho tứ giác ABCD nội tiếp đường tròn (O) và một điểm M nằm trong đường tròn.
Gọi X, Y, Z, T, U, V là hình chiếu vuông góc của M xuống AB, BC, CD, DA, AC, BD. Gọi N , P ,
Q là trung điểm của U V, XZ, Y T .Chứng minh rằng N, P, Q thẳng hàng .
Bài 4. Cho tam giác ABC với A0, B0, C0 lần lượt là trung điểm BC, CA, AB. Q là một điểm
bất kì trên mặt phẳng. M , N , P lần lượt là hình chiếu của Q lên BC, CA, AB. Chứng minh rằng
một trong hai giao điểm của đường tròn (M N P ) và đường trong (A0B0C0) là điểm anti-Steiner
của Q đối với tam giác A0B0C0.
Bài 5. Cho tam giác ABC nội tiếp đường tròn tâm (O) với N là điểm Nagel của nó. ON cắt
đường tròn (O) tại P . Chứng minh rằng đường thẳng Simson của P với tam giác ABC hoặc song
song hoặc vuông góc với HN .
Bài 6. (Định lý Sondat) Cho tam giác ABC, một đường thẳng d bất kì cắt BC, CA, AB tại
A0, B0, C0. Các đường thẳng qua A0, B0, C0 và vuông góc với BC, CA, AB cắt nhau tạo thành
tam giác A1B1C1. Chứng minh d chia đôi đường nối hai trực tâm H và H0 của tam giác ABC và A0B0C0.
Bài 7. (bài 4 Mathley round 5) Cho tam giác ABC nội tiếp trong một đường tròn (O).
Gọi P là một điểm tùy ý trong mặt phẳng tam giác. Các điểm A0, B0, C0 lần lượt đối xứng với A
qua BC, CA, AB. X là giao điểm khác A của đường tròn đường kính AP và đường tròn ngoại
tiếp tam giác AB0C0. Các điểm Y , Z được xác định tương tự. Chứng minh năm đường tròn (O),
(AB0C0), (BC0A0), (CA0B0), (XY Z) có một điểm chung.
Bài 8. Cho tam giác ABC nội tiếp đường tròn (O) với H là trực tâm. Gọi l là đường thẳng
qua H và vuông góc với OH, l1, l2, l3 lần lượt là tiếp tuyến của (O) tại A, B, C. Gọi A1 là giao
điểm của l và l1. A2 đối xứng với A1 qua A. Xác định tương tự B2, C2. Chứng minh rằng A2, B2, C2 thẳng hàng.
Bài 9. (Điểm Jarabek) Cho tam giác ABC, H là trực tâm, O là tâm đường tròn ngoại tiếp.
Chứng minh rằng các đường tròn Euler của các tam giác ABC, AHO, BHO, CHO đồng quy tại một điểm.
Bài 10. (đường tròn Hagge) Cho tam giác ABC và một điểm P bất kì. Gọi A1, B1, C1 lần
lượt là giao điểm của AP , BP , CP với đường tròn ngoại tiếp tam giác ABC. A2 đối xứng với A1
qua BC. Xác định tương tự các điểm B2, C2. Chứng minh rằng đường tròn ngoại tiếp tam giác
A2B2C2 đi qua trực tâm tam giác ABC.
Bài 11. Cho tam giác ABC nội tiếp (O). Một đường thẳng d bất kì qua O cắt AB, AC tại
Z, Y . Khi đó đường tròn đường kính BY , CZ, (O) đồng quy tại E, đường tròn đường kính BY ,
CZ và đường tròn Euler của tam giác ABC đồng quy tại F .
Bài 12. (Nguyễn Văn Linh) Cho (O), dây cung BC cố định. A chuyển động trên đường
tròn. Một điểm Q cố định trên mp. Gọi A1B1C1 là tam giác Pedal của Q ứng với tam giác ABC.
Gọi X, Y là hai giao điểm của (A1B1C1) với đường tròn Euler của tam giác ABC. P là điểm liên
hợp đẳng giác của Q trong tam giác ABC. M là 1 điểm trên đường vuông góc kẻ từ P tới BC −−→ − →
sao cho P M = u cho trước. CMR trong hai đường thẳng qua X, Y và vuông góc với XM , Y M , 19
có một đường thẳng cắt BC tại điểm cố định.
Bài 13. Cho tứ giác ABCD nội tiếp. Kí hiệu SA,SB theo thứ tự là đường thẳng Simson của
A, B đối với tam giác BCD, ACD. EA, EB theo thứ tự là đường thẳng Euler của tam giác BCD,
ACD. Chứng minh rằng: SA ⊥ EB ⇔ SB ⊥ EA.
Bài 14. (Mathley round 8) Cho tam giác ABC nội tiếp đường tròn (O) với trực tâm H.
Hai đường thẳng d1 và d2 bất kì vuông góc với nhau đi qua H. d2 cắt BC, CA, AB lần lượt tại
X1, Y1, Z1. Gọi A1B1C1 là tam giác tạo bởi đường thẳng qua X1 vuông góc với BC, qua Y1 vuông
góc với CA, qua Z1 vuông góc với AB. Tương tự xác định tam giác A2B2C2. Chứng minh rằng
đường tròn ngoại tiếp các tam giác A1B1C1 và đường tròn ngoại tiếp các tam giác A2B2C2 tiếp
xúc với nhau tại một điểm nằm trên (O).
Bài 15. (IMO 2011) Cho tam giác ABC nhọn với đường tròn ngoại tiếp Γ. l là một tiếp
tuyến của Γ và la, lb, lc lần lượt là đường thẳng đối xứng với l qua BC, CA, AB. Chứng minh
rằng đường tròn ngoại tiếp của tam giác tạo bởi la, lb, lc tiếp xúc với đường tròn Γ. Tài liệu tham khảo
[1] Các bài toán về hình học phẳng (2 tập) - V.V Praxolov
[2] Advanced Euclidean Geometry Dover Books on Mathematics - Roger A. Johnson
[3] Tài liệu giáo khoa chuyên toán - Đoàn Quỳnh (chủ biên)
[4] Một số kiến thức hình học phẳng thi Olympic - mathscope.org
[5] Episodes in nineteeth and twentith century Euclidean geometry - Ross Honsberger
[6] Tạp chí Toán Học và Tuổi Trẻ - nxb Giáo Dục. [7] Tạp chí AMM [8] Tạp chí Excalibur
[9] Tạp chí Mathematical Reflection [10] forum.mathscope.org [11] diendantoanhoc.net [12] mathlinks.ro 20