Electric Charge & Field Concepts môn Vật lý đại cương 2 | Học viện Công Nghệ Bưu Chính Viễn Thông

Introduction Course Information
Course of Physics for engineering students
(General Physics or University Physics) consists of three parts: ¾Physics I: Mechanics
Physics (Greek: physis – φύσις meaning "nature")
¾Physics II: Electromagnetics & Thermal
is the natural science which examines basic concepts Physics
such as energy, force, and spacetime and all that derives
from these, such as mass, charge, matter and its motion.
¾Physics III: Optics & Quantum Physics
http://en.wikipedia.org/wiki/Physics HUST – CTTT PH 1026 HUST – CTTT PH 1026
Course has several components: Lectures ¾Lectures
¾Discussion sections (tutorials, problem solving, quizzes)
Turn off your cell phone in lecture ¾Homework Bring your textbook ¾
Pls. NO chatting or private work in lecture
Labs: (group exploration of physical phenomena) Exams and grading: Note taking:
¾Scores on the components: homework, lab works and
•Lecture notes will be sent to your group’s mail after each lecture
mid-semester exams are counted up with the weight 0.3
¾Scores on the final exam are counted with the weight 0.7 HUST – CTTT PH 1026 HUST – CTTT PH 1026 The syllabus References links
•http://courses.physics.illinois.edu/phys212/syllabus.asp
•http://phys.lsu.edu/~jdowling/PHYS21024SP10/lectures/index.html
Lecturer contact: Communication by E-mail only
Textbook and other course material:
•Young and Freedman - University Physics with Modern Physics w Solution 13e
•Halliday, Fundamentals of Physics Extended, 8e
•Modern Physics Serway 3e w solution On-line video lecturer:
•http://ocw.mit.edu/courses/physics/8-02sc-physics-ii-electricity-
and-magnetism-fall-2010/index.htm HUST – CTTT PH 1026 Physics 2102 Spring 2007 Chapter 21 Jonathan Dowling Ph P y h s y i s c i s c s 2 1 2 0 1 2 0 2 S p S r p i r n i g n g 2 0 2 0 0 7 0 Electric Charge and Le L c e t c u t r u e r e 1 7 1 Electric Field Ch C 3 h 0 3 : 0 In I d n u d c u t c i t o i n o n an d an d I n I d n u d c u t c an t c an e c e I PowerPoint®Lectures for
University Physics, Thirteenth Edition
– Hugh D. Young and Roger A. Freedman
Lectures by Wayne Anderson HUST – CTTT PH 1026
Copyright © 2012 Pearson Education Inc. Introduction Goals for Chapter 21 •Water makes life possible as a solvent for biological
•Study electric charge & charge conservation molecules. What electrical properties allow it to do
•Learn how objects become charged this? •We now begin our study
•Calculate electric force between objects using
of electromagnetism, one Coulomb’s law of the four fundamental forces in Nature.
•Learn distinction between electric force and •We start with electric electric field charge and electric fields. HUST – CTTT PH 1026 HUST – CTTT PH 1026 Goals for Chapter 21 Electric charge •Two positive or two
•Calculate the electric field due to many charges negative charges repel each other.
•Visualize and interpret electric fields A positive charge and a negative charge attract each other.
•Calculate the properties of electric dipoles •Check out: http://www.youtube.com/wat ch?v=45AAIl9_lsc HUST – CTTT PH 1026 HUST – CTTT PH 1026 Electric charge Electric charge •Two positive or two negative charges repel •Two positive or two each other. negative charges repel each other. A positive charge and a negative charge attract A positive charge and each other. a negative charge attract each other. •Check out Balloons in PhET simulations HUST – CTTT PH 1026 HUST – CTTT PH 1026
Laser printer & Photocopier
Electric charge and the structure of matter
•A laser printer makes use of forces between charged bodies. •The particles of the atom are the negative electron, the positive proton, and the uncharged neutron. HUST – CTTT PH 1026 HUST – CTTT PH 1026 Atoms and ions Atoms and ions
•A neutral atom has the same number of protons as electrons.
•A positive ion is an atom with one or more electrons removed.
A negative ion has gained one or more electrons. HUST – CTTT PH 1026 HUST – CTTT PH 1026 Conservation of charge
Conductors and insulators
•The proton and electron have the same magnitude charge.
•A conductor permits the
•The magnitude of charge of the electron or proton is a easy movement of charge
natural unit of charge. All observable charge is through it. quantized in this unit.
•An insulator does not.
•The universal principle of charge conservation states
that the algebraic sum of all the electric charges in any closed system is constant. HUST – CTTT PH 1026 HUST – CTTT PH 1026
Conductors and insulators
Conductors and insulators
•A conductor permits the easy movement of charge through it. An insulator does not.
•A conductor permits the easy movement of charge
through it. An insulator •Most metals are good does not. conductors, while most nonmetals are insulators. •Most metals are good conductors, while most •Semiconductors are nonmetals are insulators. intermediate in their properties between good conductors and good insulators. HUST – CTTT PH 1026 HUST – CTTT PH 1026 Charging by induction Charging by induction
•The negative rod is able to charge the metal ball without losing
•The negative rod is able to charge the metal ball without losing any of its own charge. any of its own charge. HUST – CTTT PH 1026 HUST – CTTT PH 1026 Charging by induction
Electric forces on uncharged objects
•The negative rod is able to charge the metal ball without losing
•The charge within an insulator can shift slightly. As a result, an any of its own charge.
electric force *can* be exerted upon a neutral object. HUST – CTTT PH 1026 HUST – CTTT PH 1026
Electric forces on uncharged objects Electrostatic painting
•Induced positive charge on the metal object attracts the
negatively charged paint droplets. Check out
http://www.youtube.com/watch?feature=endscreen&v=zTwkJBtCcBA&NR=1 HUST – CTTT PH 1026 HUST – CTTT PH 1026
Coulomb’s law – Electric FORCE Coulomb’s law
The magnitude of electric force bet-
ween two point charges is directly •Mathematically:
proportional to the pro-duct of their
charges and inversely proportional
F = k|q1q2|/r2
to the square of the distance between them.
= (1/4πε0)|q1q2|/r2 •A VECTOR •Magnitude •Direction •Units HUST – CTTT PH 1026 HUST – CTTT PH 1026 Coulomb’s law
Measuring the electric force between point charges •Mathematically: Example 21.1 compares the F = k|q electric and gravitational 1q2|/r2 forces.
= (1/4πε0)|q1q2|/r2
An alpha particle has mass m = 6.64 x 10-
27 kg and charge q = +2e = 3.2 x 10-19 C. •k = 9 x 109Nm2/C2
Compare the magnitude of the electric
repulsion between two alpha particles and
∀ε0 = 8.85 x 10 – 12 C2/Nm2 their gravitational attraction HUST – CTTT PH 1026 HUST – CTTT PH 1026
Force between charges along a line
Force between charges along a line
•Example 21.2 for two charges:
•Example 21.3 for three charges:
Two point charges, q1 = +25nC, and q2 = -75 nC,
Two point charges, q1 = +1.0nC at x = +2.0 cm, and
separated by r = 3.0 cm. What is the Force of q1 on
q2 = -3.0 nC at x = +4.0 cm. What is the Force of q1
q2? What is the force of q2 on q1?
and q2 on q3 = + 5.0 nC at x = 0? HUST – CTTT PH 1026 HUST – CTTT PH 1026
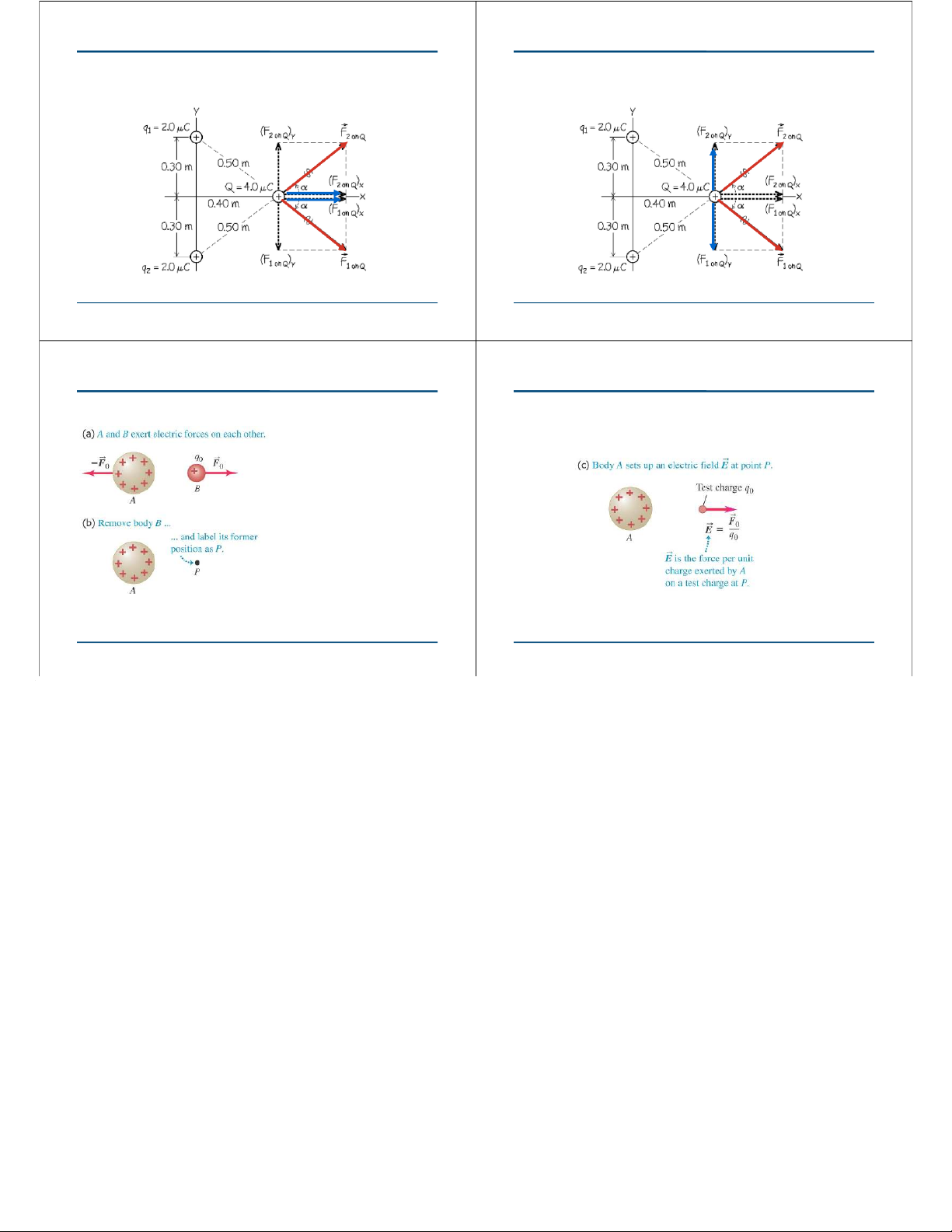
Vector addition of electric forces
Vector addition of electric forces
•Example 21.4 shows that we must use vector addition when
•Example 21.4 shows that we must use vector addition when adding electric forces. adding electric forces.
Two equal positive charges, q1 = q2 = +2.0µCare
located at x=0, y = 0.30 m and x=0, y = -.30 m respectively.
What is the Force of q1 and q2 on Q = + 5.0 µC at x = 0.40 m, y = 0? HUST – CTTT PH 1026 HUST – CTTT PH 1026
Vector addition of electric forces
Vector addition of electric forces
•Example 21.4 shows that we must use vector addition when
•Example 21.4 shows that we must use vector addition when adding electric forces. adding electric forces. HUST – CTTT PH 1026 HUST – CTTT PH 1026 Electric field Electric field
•A charged body produces an electric field in the space around it
•We use a small test charge q0to find out if an electric field is present. HUST – CTTT PH 1026 HUST – CTTT PH 1026 Electric field
Definition of the electric field
•We use a small test charge q0to find out if an electric field is
•E fields are VECTOR fields – and solutions to present.
problems require magnitude, direction, and units. HUST – CTTT PH 1026 HUST – CTTT PH 1026
Definition of the electric field
Electric field of a point charge
•E fields are VECTOR fields – and solutions to
•E fields from positive charges point AWAY from the charge
problems require magnitude, direction, and units.
•E fields point in the direction a POSITIVE test charge would move! HUST – CTTT PH 1026 HUST – CTTT PH 1026
Electric field of a point charge
Electric-field vector of a point charge
•E fields point TOWARDS a negative charge •Example 21.6 - the vector nature of the electric field.
•E fields point in the direction a POSITIVE test charge would move!
•Step 1: Coordinate System! •Step 2: SKETCH! HUST – CTTT PH 1026 HUST – CTTT PH 1026
Electric-field vector of a point charge
Electric-field vector of a point charge •Example 21.6 - the vector •Example 21.6 - the vector nature of the electric field. nature of the electric field.
•Step 1: Coordinate System!
•Step 1: Coordinate System! θ θ •Step 2: Sketch! •Step 2: Sketch! •Step 3: COMPONENTS!! •Step 3: COMPONENTS!!
–Ex= kq/r2 cos (θ) (-x dir)
–Ex= kq/r2 cos (θ) i(-x dir)
–Ey= kq/r2 sin (θ) (+y dir)
–Ey= kq/r2 sin (θ) j (+y dir)
•E = -11 N/C i+ 14 N/C j HUST – CTTT PH 1026 HUST – CTTT PH 1026
Electron in a uniform field- Ex 21.7
Electron in a uniform field- Ex 21.7
•Uniform field between two charged plates;
•What is acceleration of single electron in field?
•Electrical “pressure” (voltage!) from battery
•What speed and KE after 1.0 cm? How much time? HUST – CTTT PH 1026 HUST – CTTT PH 1026
Superposition of electric fields
Superposition of electric fields
•The total electric field at a point is the vector sum of the fields due
•The total electric field at a point is the vector sum of the fields due to all the charges present. to all the charges present.
•For discrete charges: E = Σ(kqi/ri3)ri = Σ(kqi/ri2) ri
•For *continuous charge distributions* E = ∫k(dqi/ri2) ri
•START by finding dE from a infinitesimal charge dq in an
infinitesimal element of length (ds), area (dA), or volume (dV)
•Integrate over all dq in a line, surface, or volume. HUST – CTTT PH 1026 HUST – CTTT PH 1026
Superposition of Infinitesimal charge elements:
Superposition of Infinitesimal charge elements:
•E-Field of a linear ring (radius = a) of charge Qat
•Field of a linear ring of charge
some point P a distance x away?
•What is dQ in a tiny segment ds? –Total Charge Q ds Total charge Q –Total length = 2πa a a E –Charge/length = λ P=? Px –λ = Q/ 2πa •dQ = λds HUST – CTTT PH 1026 HUST – CTTT PH 1026
Ex 21.9 – Field of charged line segment
Ex 21.10 - Field of a charged line segment
•Field of a linear ring of charge •More challenging!
•The point P is no longer the SAME distance away from every element ds!! HUST – CTTT PH 1026 HUST – CTTT PH 1026
Ex. 21.11 – Field of disk of charge
Field of two oppositely charged infinite sheets
•Treat the disk as superposition of multiple rings of •Follow Example 21.12.
thickness dr! ⇒dQ here: σda = σ(2πr)dr HUST – CTTT PH 1026 HUST – CTTT PH 1026 Electric field lines
Electric field lines of point charges
•An electric field line is an imaginary line or curve
•Electric field lines of a single point charge and for two charges of
whose tangent at any point is the direction of the electric
opposite sign and of equal sign.
field vector at that point. (See Figure 21.27 below.) HUST – CTTT PH 1026 HUST – CTTT PH 1026 Electric dipoles Dipole electric fields
•The total electric field at a point is the vector sum of the fields due to all the charges present.
•An electric dipole is a pair of point charges having equal but opposite sign and separated by a distance. •Water molecules form an electric dipole. HUST – CTTT PH 1026 HUST – CTTT PH 1026
Ex 21.14 - Electric field of a dipole
Force and torque on a dipole
•What is E at a distance y from a dipole separated by a
•A dipole in an electric field can rotate!
distance d (and dipole moment P= qd)?
•The field exerts a torque on the dipole about its center.
•F = qEand τ= rx Fwith magnitude (d q)Esin( φ)
•Define p = qd, direction palong dipole – to plus + HUST – CTTT PH 1026 HUST – CTTT PH 1026