Experimental Report 3: Inductor & Free Oscillation in RLC Circuit môn Vật lý đại cương 2 | Học viện Công Nghệ Bưu Chính Viễn Thông

Experimental Report 3
INDUCTOR AND FREE OSCILLATION IN RLC CIRCUIT
Verification of the instructors Group: 04
Name: Nguyễn Nhật Minh Student ID: 20224347 I. Experiment Motivations
-Understanding the current across an inductor-resistor and RLC circuit.
-Calculating the energy of the oscillation RLC circuit. II. Experimental result
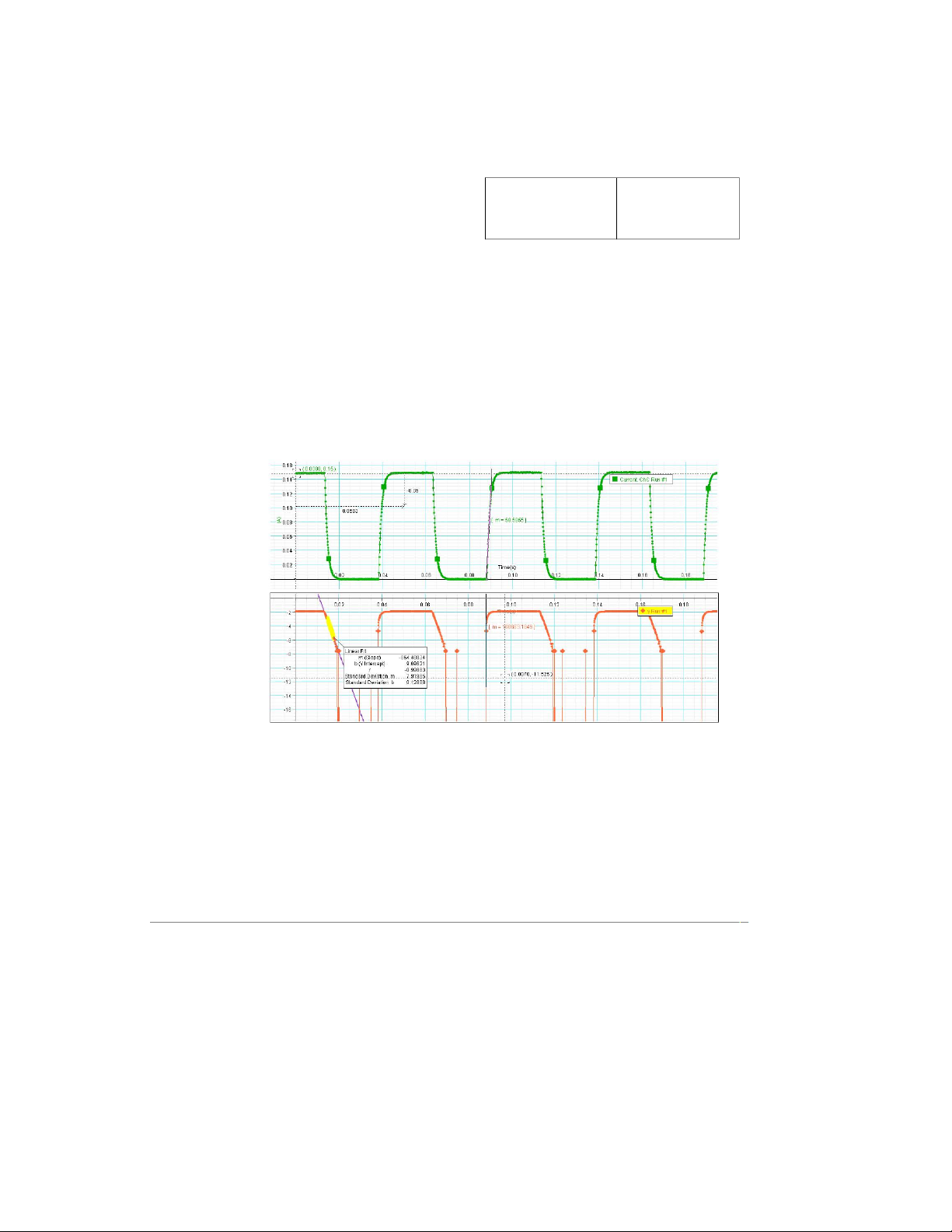
Part 1: Resistance and Inductance of the coil a. Without core VS=1(V) I0 = 0.15 (A) Slope S = -864.48834
The resistance of the coil:
RL=VS =10.15 ≈6.67(Ω) IO Coil inductance :
LW/O=VSIO×S=1 0.15×864=7.72×10−3(H) b. With core VS=1(V) I0 = 0.14 (A) Slope S = -173,20136
The resistance of the coil:
RL=VS =10.14 ≈7.14(Ω) IO Coil inductance : LW/O=VS
IO×S=1 0.14×173=41.3×10−3(H)
Explain: Once the core is inserted into the coil, the coil's inductance rises
dramatically from 7.72mH to 41.3mH. This happens because the core has a
higher permeability than air, allowing magnetic fields to pass through the core
more easily, which in turn enhances the coil's inductance.
Part 2: Free oscillation of the RLC circuit a. Frequency
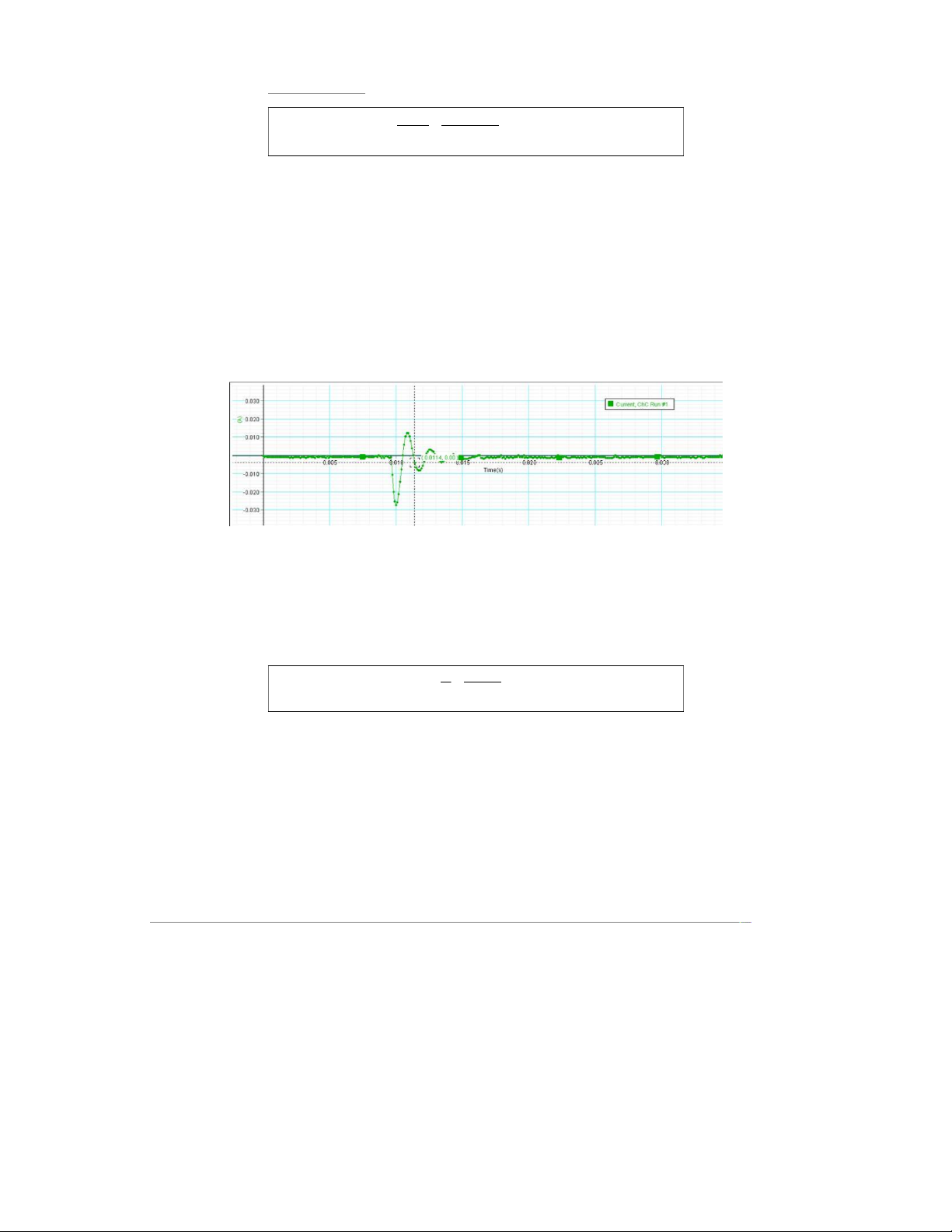
The current in RLC circuit: t1 = 0.0113 (s) t2 = 0.0129 (s) T = t1 - t2 = 0.0016 (s)
The frequency based on the graph:
fmeasured=1T=10.0016=625(Hz)
LW/O=¿ 7.72 mH=7.83× 10−3 H C=10-5 F=0.00001 F
The frequency based on theoretical calculation: fprediction=1 LC=1 7.72×10−3 10 × −5=572.81(Hz ) 2π √ 2×3.14× √ Comparison:
Δf=fprediction−fmeasured=625−572.81=52.19(Hz) b. Energy
The total energy in RLC circuit:
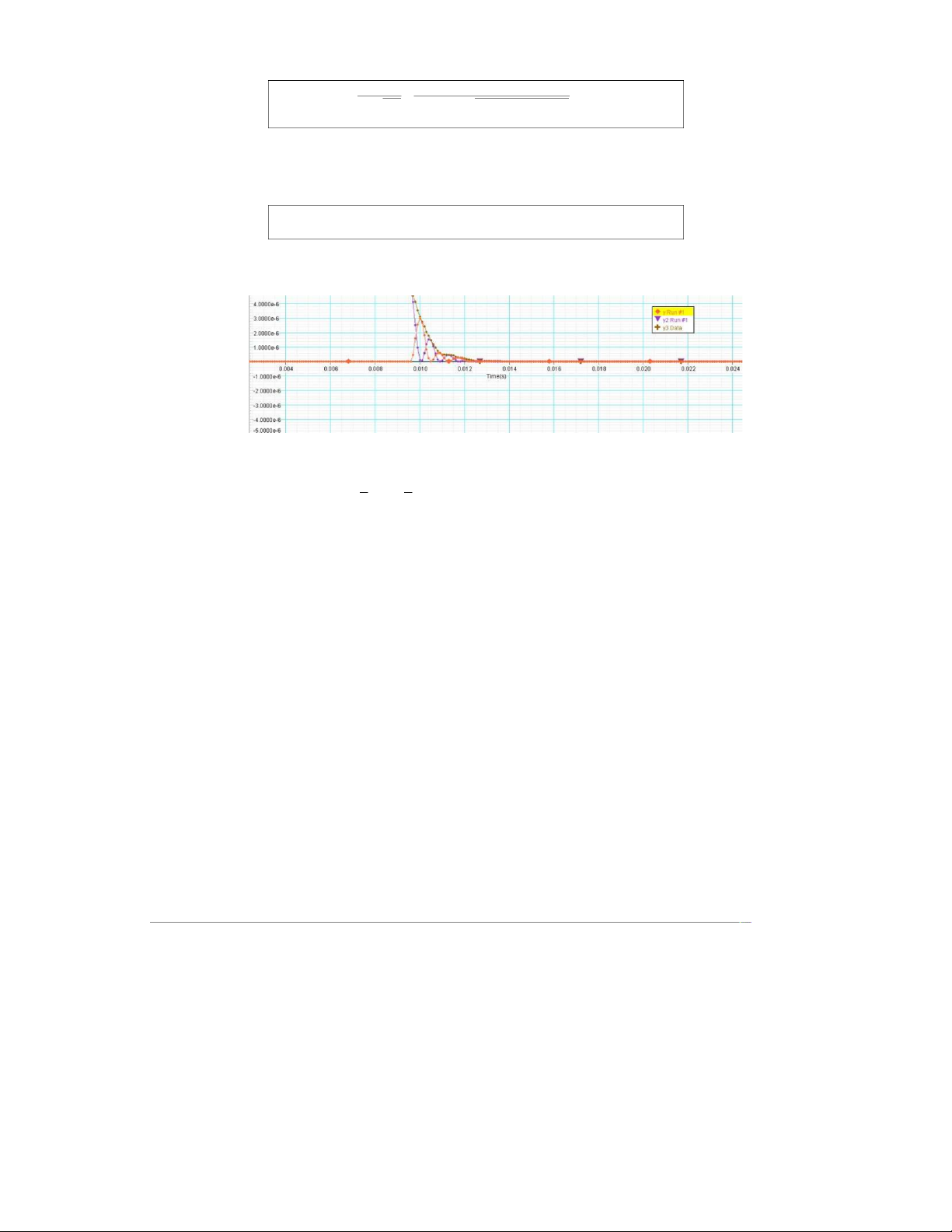
U=Uc+UL=1 2CV2+1 2LI2 = 8.1× 10−5 (J) Comment:
- After stopping the electric power, the energy of the circuit does not
decrease rapidly to zero, it reduces to zero over a short period of time.
- The energy of oscillations of the coil and the capacitor are damped oscillations. Explain:
The energy of the circuit loses by the heat of the resistor at rate i2R
The graph of total energy is steepest at the time that the magnetic
energy reaches a local maximum because in these times, the current
through the coil is highest, and the loss of energy is mainly due to the resistance of the coil.