

















Preview text:
20 Chemical Kinetics C O N T E N T S
20-1 Rate of a Chemical Reaction 20-7 Reaction Kinetics: A Summary 20-2 Measuring Reaction Rates 20-8
Theoretical Models for Chemical LEARNING OBJECTIVES
20-3 Effect of Concentration on Reaction Kinetics
20.1 Express the rate of reaction in terms Rates: The Rate Law 20-9 The Effect of Temperature on
of the rate of appearance or the rate of 20-4 Zero-Order Reactions Reaction Rates disappearance of a substance. 20-5 First-Order Reactions 20-10 Reaction Mechanisms
20.2 Explain how a graph of concentration 20-6 Second-Order Reactions 20-11 Catalysis
versus time can be used to determine the
rate of reaction at any instant.
20.3 Describe how the method of initial
rates can be used to determine the rate law for a reaction.
20.4 Use the rate law for a zero-order
reaction, together with experimental data,
to obtain the rate constant for a zero-order reaction.
20.5 Use the rate law for a first-order
reaction to determine the rate constant or half-life of a reaction.
20.6 Identify the integrated rate law for a
second-order reaction, and derive the C
relationship between half-life and rate Y constant.
20.7 Summarize the differences between hotographs, N
zero-order, first-order, and second-order ental P reactions.
20.8 Discuss the significance of the innot/Fundam
activation energy for a reaction, and
describe the reaction profile for both Joseph P. S
endothermic and exothermic reactions.
Although stable at room temperature, ammonium dichormate decomposes very
20.9 Discuss the Arrhenius equation and rapidly once ignited:
how it can be used to estimate the
1NH422Cr2O71s2 ¢ " N21g2 + 4 H 2O1g2 + Cr2O31s2
activation energy for a reaction.
The rates of chemical reactions and the effect of temperature on those rates are
20.10 Describe the general structure of a
among several key concepts explored in this chapter.
reaction profile for a two-step mechanism,
and describe what is meant by the rate- determining step.
20.11 Explain the role played by a
catalyst, and describe how enzymes perform this task.
Rocket fuel is designed to give a rapid release of gaseous products
and energy to provide a rocket maximum thrust. Milk is stored in a
refrigerator to slow down the chemical reactions that cause it to
spoil. Current strategies to reduce the rate of deterioration of the ozone
layer try to deprive the ozone-consuming reaction cycle of key intermedi-
ates that come from chlorofluorocarbons (CFCs). Catalysts are used to
reduce the harmful emissions from internal combustion engines that con-
tribute to smog. These examples illustrate the importance of the rates of
chemical reactions. Moreover, how fast a reaction occurs depends on the 922 20-1 Rate of a Chemical Reaction 923
reaction mechanism—the step-by-step molecular pathway leading from reac-
tants to products. Thus, chemical kinetics concerns how rates of chemical
reactions are measured, how they can be predicted, and how reaction-rate
data are used to deduce probable reaction mechanisms.
The chapter begins with a discussion of the meaning of a rate of reaction and
some ideas about measuring rates of reaction. This is followed by the introduc-
tion of mathematical equations, called rate laws, that relate the rates of reac-
tions to the concentrations of the reactants. Finally, with this information as
background, we will turn to one of our central purposes of this chapter: relat-
ing rate laws to plausible reaction mechanisms. 20-1 Rate of a Chemical Reaction
Rate, or speed, refers to something that happens in a unit of time. A car travel-
ing at 60 km/h, for example, covers a distance of 60 kilometers in one hour.
For chemical reactions, the rate of reaction describes how fast the concentra-
tion of a reactant or product changes with time.
To illustrate, let’s consider the reaction that begins immediately after the ions and Sn2+ Fe3+
are simultaneously introduced into water.
2 Fe3+1aq2 + Sn2+1aq2 ¡ 2 Fe2+1aq2 + Sn4+1aq2 (20.1)
Suppose that 38.5 s after the reaction starts, 3Fe2+4 is found to be 0.0010 M. Recall that the symbol ▲ 3 4
During the period of time, ¢t = 38.5 s, the change in concentration of Fe2+,
means “concentration.” Also,
which we designate as ¢3Fe2+4, is ¢3Fe2+4 = 0.0010 M - 0 M = 0.0010 M. ¢ means “the change in,”
The average rate at which Fe2+ is that is, the final value minus
formed in this interval is the change in concentration of Fe2+ divided by the the initial value. change in time. ¢3Fe2+4 0.0010 rate M of formation of Fe2+ = = = 2.6 * 10-5 M s-1 ¢t 38.5 s
How has the concentration of Sn4+ changed during the 38.5 s we were moni- toring the
Can you see that in 38.5 s, ¢3Sn4+ Fe2+? 4 will be 0.00050 M - 0 M= Because only one
ion is produced for every two Fe2+ Sn4+ 0.00050 M? ions, the
buildup of 3Sn4+4 will be only one-half that of 3Fe2+4. Consequently the rate of formation of Sn4+ is 0.00050 M rate of formation of Sn4+ = = 1.3 * 10-5 M s-1 38.5 s
We can also follow the course of the reaction by monitoring the concentra-
tions of the reactants. Thus, the amount of Fe3+ consumed is the same as the amount of
produced. The change in concentration of Fe3+ Fe2+ is
The concentration change is negative because Fe3+ ¢3Fe3+4 = -0.0010 M. is
consumed by the reaction. Thus, ¢3Fe3+4 -0.0010 M = = - 2.6 * 10-5 M s-1 ¢t 38.5 s
The quantity above is the average rate of change of change of 3Fe3+4 in this inter-
val. It is a negative quantity because 3Fe3+4 decreases with time. The average rate
of disappearance of Fe3+ is defined as follows. ¢3Fe3+4
rate of disappearance of Fe3+ = - = 2.6 * 10-5 M s-1 ¢t
Why is a negative sign incorporated into the definition of rate in this case? It is
because the term “rate of disappearance” implies that 3Fe3+4 decreases with
time. When told the rate of disappearance of is 2.6 * 10-5 M s-1 Fe3+ , we 924 Chapter 20 Chemical Kinetics
know the rate of change of concentration must be -2.6 * 10-5 M s-1.
In the same way that we related the rate of formation of Sn4+ to that of Fe2+,
we can relate the rate of disappearance of Sn2+ to that of Fe3+. That is, the rate of
disappearance of Sn2+ is half that of Fe3+, giving
rate of disappearance of Sn2+ = 1.3 * 10-5 M s-1
When we refer to the rate of reaction (20.1), which of the four quantities
described should we use? To avoid confusion in this matter, the International
Union of Pure and Applied Chemistry (IUPAC) recommends that we use a gen-
eral rate of reaction, which, for the hypothetical reaction represented by the bal- anced equation,
a A + b B + Á ¡ g G + h H + Á is 1 ¢3A4 1 ¢3B4 1 ¢3G4 1 ¢3H4 rate of reaction = - = - = = (20.2) a ¢t b ¢t g ¢t h ¢t
In this expression, we take the negative value of ¢3X4>¢t, when X refers to a
reactant to ensure that the rate of reaction is a positive quantity. To obtain a sin-
gle, positive quantity it is necessary to divide all rates by the appropriate stoi-
chiometric coefficients. If we apply this expression to reaction (20.1), we obtain 1 ¢3Fe3+4 ¢3Sn2+4 rate of reaction = - = - 2 ¢ t ¢t 1 ¢3Fe2+4 ¢3Sn4+4 = = = 1.3 * 10-5 M s-1 2 ¢t ¢t EXAMPLE 20-1
Expressing the Rate of a Reaction
Suppose that at some point in the reaction A + 3 B ¡ 2 C + 2 D
3B4 = 0.9986 M,and that 13.20 min later 3B4 = 0.9746 M.What is the average rate of reaction during this time period, expressed in M s-1? Analyze
This is a straightforward application of the definition for rate of reaction, expression (20.2). To formulate the
rate, we use ¢3B4 = 0.9746 M - 0.9986 M = -0.0240 M and ¢t = 13.20 min. Solve The solution is 1 ¢3B4 1 -0.0240 average rate M of reaction = - = - * = 6.06 * 10-4 3 M min -1 ¢t 3 13.20 min
To express the rate of reaction in moles per liter per second, we must convert from min-1 to s-1. We can do
this with the conversion factor 1 min>60 s. 1 min rate of reaction = 6.06 * 10-4 - M min 1 * = 1.01 * 10-5 M s-1 60 s
Alternatively, we could have converted 13.20 min to 792 s and used ¢t = 792 s in evaluating the rate of reaction. Assess
By monitoring changes in concentration over a time period, we can obtain the average rate of reaction.
Remember that the rate of reaction can be defined in terms of any reactant or product. PRACTICE EXAMPLE A:
At some point in the reaction 2 A + B ¡ C + D, 3A4 = 0.3629 M. At a time 8.25 min
later 3A4 = 0.3187 M. What is the average rate of reaction during this time interval, expressed in M s-1? PRACTICE EXAMPLE B: In the reaction 2 A ¡
3 B, 3A4 drops from 0.5684 M to 0.5522 M in 2.50 min. What is
the average rate of formation of B during this time interval, expressed in M s-1? 20-2 Measuring Reaction Rates 925 20-1 CONCEPT ASSESSMENT
In the reaction of gaseous nitrogen and hydrogen to form gaseous ammonia, what
are the relative rates of disappearance of the two reactants? How is the rate of
formation of the product related to the rates of disappearance of the reactants? KEEP IN MIND that according to expression 20-2 Measuring Reaction Rates
(20.2), the rate of this reaction can be expressed either
To determine a rate of reaction, we need to measure changes in concentration as rate of disappearance of
over time. A change in time can be measured with a stopwatch or other timing H2O2 or 2 * rate of formation of O g .
device, but how do we measure concentration changes during a chemical 21 2
reaction? Also, why is the term average used in referring to a rate of reaction?
These are two of the questions that are answered in this section. Following a Chemical Reaction
The decomposition of hydrogen peroxide, a common antiseptic, results in the formation of water and O21g2* 1 H2O21aq2 ¡ H2O1l2 + (20.3) 2 O21g2
We can follow the progress of the reaction by focusing either on the formation
of O21g2 or on the disappearance of H2O2. For example, we can
• Measure the volumes of O21g2 produced at different times and relate
these volumes to decreases in concentration of H2O2 (Fig. 20-1).
• Remove small samples of the reaction mixture from time to time, and
analyze these samples for their H O
2 2 content. One way to do this is by
titration with KMnO4 in acidic solution. The net ionic equation for this
oxidation–reduction reaction is 2 MnO - 4 1aq2 + 5 H2O 1
2 ¡ Mn2+1aq2 + 8 H2O1l2 + 5 O21g2 2 aq2 + 6 H+1aq 2 ▲ FIGURE 20-1 (20.4) Experimental setup for determining the rate of
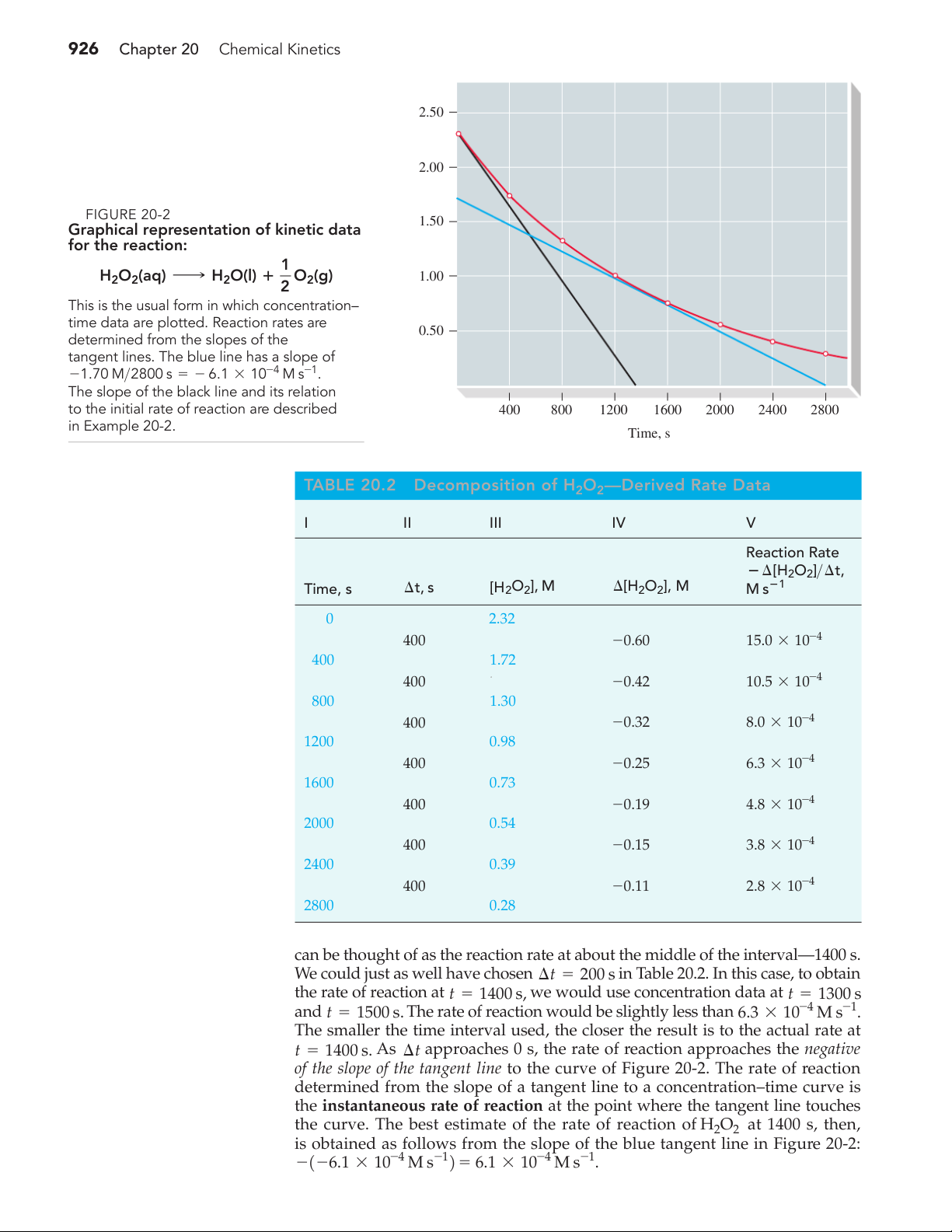
Table 20.1 lists typical data for the decomposition of H O 2 2, and Figure 20-2 decomposition of H O 2 2
displays comparable data graphically. Oxygen gas given off by the reaction mixture is trapped, and its volume is measured
Rate of Reaction Expressed as Concentration in the gas buret. The amount Change over Time of H2O2 consumed and the
Some data extracted from Figure 20-2 are listed in Table 20.2 (in blue). Column III remaining concentration of lists the concentration of H H2O2 can be calculated
2O2 at the times shown in column I. Column II lists from the measured volume
the arbitrary time interval between data points—400 s. Column IV reports the of O g .
concentration changes that occur for each 400 21 2
s interval. The rates of reaction,
expressed as the rate of disappearance of H2O ,2 are shown in column V. The
data show that the reaction rate is not constant—the lower the remaining con- TABLE 20.1
centration of H2O ,2 the more slowly the reaction proceeds. Decomposition of H2O2
Rate of Reaction Expressed as the Slope of a Tangent Line Time, s [H2O2], M
When the rate of reaction is expressed as - ¢3H2O24>¢t, the result is an average 0 2.32
value for the time interval ¢t. For example, in the interval from 1200 to 1600 s, 200 2.01
the rate averages 6.3 * 10-4 M s-1 (fourth entry in column V of Table 20.2). This 400 1.72 600 1.49 1200 0.98
*Although reaction (20.3) goes to completion, it does so very slowly. Generally, a catalyst is used 1800 0.62
to speed up the reaction. We describe the catalysis in this reaction in Section 20-11. When H 3000 0.25
2O21aq2 is applied to an open wound, the enzyme catalase in blood catalyzes its decomposition. 926 Chapter 20 Chemical Kinetics 2.50 2.00 ▲ /L FIGURE 20-2 ol 1.50
Graphical representation of kinetic data ], m for the reaction: 2O2 1 H O H [H 2 2(aq) ¡ 2O(l) ⴙ O 1.00 2 2(g)
This is the usual form in which concentration–
time data are plotted. Reaction rates are 0.50
determined from the slopes of the
tangent lines. The blue line has a slope of
-1.70 M>2800 s = - 6.1 * 10-4 M s-1.
The slope of the black line and its relation
to the initial rate of reaction are described 400 800 1200 1600 2000 2400 2800 in Example 20-2. Time, s TABLE 20.2
Decomposition of H O —Derived Rate Data 2 2 I II III IV V Reaction Rate ⴚ ¢[H2O2]>¢t, Time, s ¢t, s [H2O2], M ¢[H2O2], M M sⴚ1 0 2.32 400 -0.60 15.0 * 10-4 400 1.72 400 a -0.42 10.5 * 10-4 800 1.30 400 -0.32 8.0 * 10-4 1200 0.98 400 -0.25 6.3 * 10-4 1600 0.73 400 -0.19 4.8 * 10-4 2000 0.54 400 -0.15 3.8 * 10-4 2400 0.39 400 -0.11 2.8 * 10-4 2800 0.28
can be thought of as the reaction rate at about the middle of the interval—1400 s.
We could just as well have chosen ¢t = 200 s in Table 20.2. In this case, to obtain
the rate of reaction at t = 1400 s, we would use concentration data at t = 1300 s and
The rate of reaction would be slightly less than 6.3 * 10-4 M s-1 t = 1500 s. .
The smaller the time interval used, the closer the result is to the actual rate at
t = 1400 s. As ¢t approaches 0 s, the rate of reaction approaches the negative
of the slope of the tangent line to the curve of Figure 20-2. The rate of reaction
determined from the slope of a tangent line to a concentration–time curve is
the instantaneous rate of reaction at the point where the tangent line touches
the curve. The best estimate of the rate of reaction of H2O2 at 1400 s, then,
is obtained as follows from the slope of the blue tangent line in Figure 20-2: 6.1 * 10-4 M s-1 -1-6.1 * 10-4 M s-12 = . 20-2 Measuring Reaction Rates 927
To better understand the difference between average and instantaneous reac-
tion rates, think of taking a 190 km highway trip in 2.00 h. The average speed is
95 km/h. The instantaneous speed is the speedometer reading at any instant. 20-1 ARE YOU WONDERING?
How do we differentiate between the average rate of
reaction and the instantaneous rate?
If you are familiar with differential calculus, you probably know the answer. If the
rate of reaction (20.3) is written as - ¢3H O 2 24 lim ¢t ¡ 0 ¢t
the delta quantities can be replaced by the differentials -d3H2O24 and d ,t leading to the expression -d3H2O24 dt
Thus, the delta notation (not taken to the limit of ¢t ¡ ) 0 signifies an average
rate and the differential notation, an instantaneous rate. Initial Rate of Reaction
Sometimes we simply want to find the rate of reaction when the reactants are
first brought together—the initial rate of reactio .
n This rate can be obtained from
the tangent line to the concentration–time curve at t = 0. An alternative way is to
measure the concentration of the chosen reactant as soon as possible after mix-
ing, in this way obtaining ¢3reactant4 for a very short time interval 1¢t2 at
essentially t = 0. These two approaches give the same result if the time interval
used is limited to that in which the tangent line and the concentration-time curve
practically coincide. In Figure 20-2 this condition occurs for about the first 200 s. EXAMPLE 20-2
Determining and Using an Initial Rate of Reaction
From the data in Table 20.2 and Figure 20-2 for the decomposition of H2O2, determine (a) the initial rate of
reaction, and (b) 3H2O24t at t = 100 s, assuming that the initial rate is constant for at least 100 s. Analyze
To determine the initial rate of reaction from the slope of the tangent line in part (a), we use the intersection of
the black tangent line with the axis. In part (b) we will assume that the rate determined in (a) remains essen-
tially constant for at least 100 s. Solve
(a) t = 0, 3H2O24 = 2.32 M; t = 1360 s, 3H2O24 = 0. -10 - 2.322 M
initial rate of reaction = -1slope of tangent line2 = 11360 - 20 s = 1.71 * 10-3 M s-1
An alternative method is to use data from Table 20.1: 3H2O24 = 2.32 M at t = 0 and 3H2O24 = 2.01 M at t = 200 s. - ¢3H2O24 -12.01 - 2 2.32 M initial rate = = ¢t 200 s = 1.55 * 10-3 M s-1 (continued) 928 Chapter 20 Chemical Kinetics (b) Since - ¢3H2O24 rate of reaction = ¢t then - ¢3H2O24 1.71 * 10-3 M s-1 = 100 s -11.71 * 10-3 -
M s 121100 s2 = ¢3H2O24 = 3H2O 4 2 t - 3H2O 4 2 0
-1.71 * 10-1 M = 3H2O24t - 2.32 M
3H2O24t = 2.32 M - 0.17 M = 2.15 M Assess
In part (a) the agreement between the two methods is fairly good, although it might be better if the time inter-
val were shorter than 200 s. Of the two results, the one based on the tangent line is presumably more precise
because it is expressed with more significant figures. However, the reliability of the tangent line depends on
how carefully the tangent line is constructed. Another reason for favoring a graphical method is that it tends to
minimize the effect of errors that may be found in individual data points. In part (b) if we had used initial rate
= 1.6 * 10-3 M s-1, we would have calculated 3H2O24t = 2.16 M. PRACTICE EXAMPLE A:
For reaction (20.3), determine (a) the instantaneous rate of reaction at 2400 s and (b) 3H2O24
at 2450 s. [Hint: Assume that the instantaneous rate of reaction at 2400 s holds constant for the next 50 s.] PRACTICE EXAMPLE B:
Use data only from Table 20.2 to determine 3H2O24 at t = 100 s. Compare this value with
the one calculated in Example 20-2(b). Explain the reason for the difference. 20-2 CONCEPT ASSESSMENT
As shown later in the chapter, for certain reactions the initial and instantaneous
rates of reaction are equal throughout the course of the reaction. What must be
the shape of the concentration–time graph for such a reaction? 20-3
Effect of Concentration on Reaction Rates: The Rate Law
One of the goals in a chemical kinetics study is to derive an equation that can
be used to predict the relationship between the rate of reaction and the con-
centrations of reactants. Such an experimentally determined equation is called ▲ Rate laws are obtained
a rate law, or rate equation. experimentally and thus, are
Consider the hypothetical reaction empirical.
a A + b B + Á ¡ g G + h H + Á (20.5)
where a, b, Á stand for coefficients in the balanced equation. The rate law for
reaction (20.5) can often be expressed in the following general form.*
rate of reaction = k3A4m3B4n Á (20.6)
The terms 3A4, 3B4, Á represent reactant molarities. The required exponents, m n
, , Á are generally small, positive whole numbers, although in some cases
*We assume that reaction (20.5) goes to completion. If it is reversible, the form of the rate equa-
tion is more complex than that given in equation (20.6). Even for reversible reactions, though,
equation (20.6) applies to the initial rate of reaction because in the early stages of the reaction
there are not enough products for a significant reverse reaction to occur. 20-3
Effect of Concentration on Reaction Rates: The Rate Law 929
they may be zero, fractional, or negative. They must be determined by experi-
ment and are generally not related to stoichiometric coefficients a, b, Á . That
is, often m Z a, n Z b, and so on.
The term order is related to the exponents in the rate law and is used in two
ways: (1) If m = 1, we say that the reaction is first order in A. If n = 2, the reac-
tion is second order in B, and so on. (2) The overall order of reaction is the sum
of all the exponents: m + n + Á . The proportionality constant k relates the
rate of reaction to reactant concentrations and is called the rate constant of the
reaction. Its value depends on the specific reaction, the presence of a catalyst
(if any), and the temperature. The larger the value of k, the faster a reaction goes. A common misconception ▲
The order of the reaction establishes the general form of the rate law and the
is that rate and k are the same.
appropriate units of k (that is, depending on the values of the exponents). As equation (20.6) clearly
With the rate law for a reaction, we can
shows, rate Z k in general.
The rate constant, k, is one of
• calculate rates of reaction for known concentrations of reactants
the factors affecting the rate of reaction but not the only one.
• derive an equation that expresses a reactant concentration as a function of time
But how do we establish the rate law? We need to use experimental data of the type
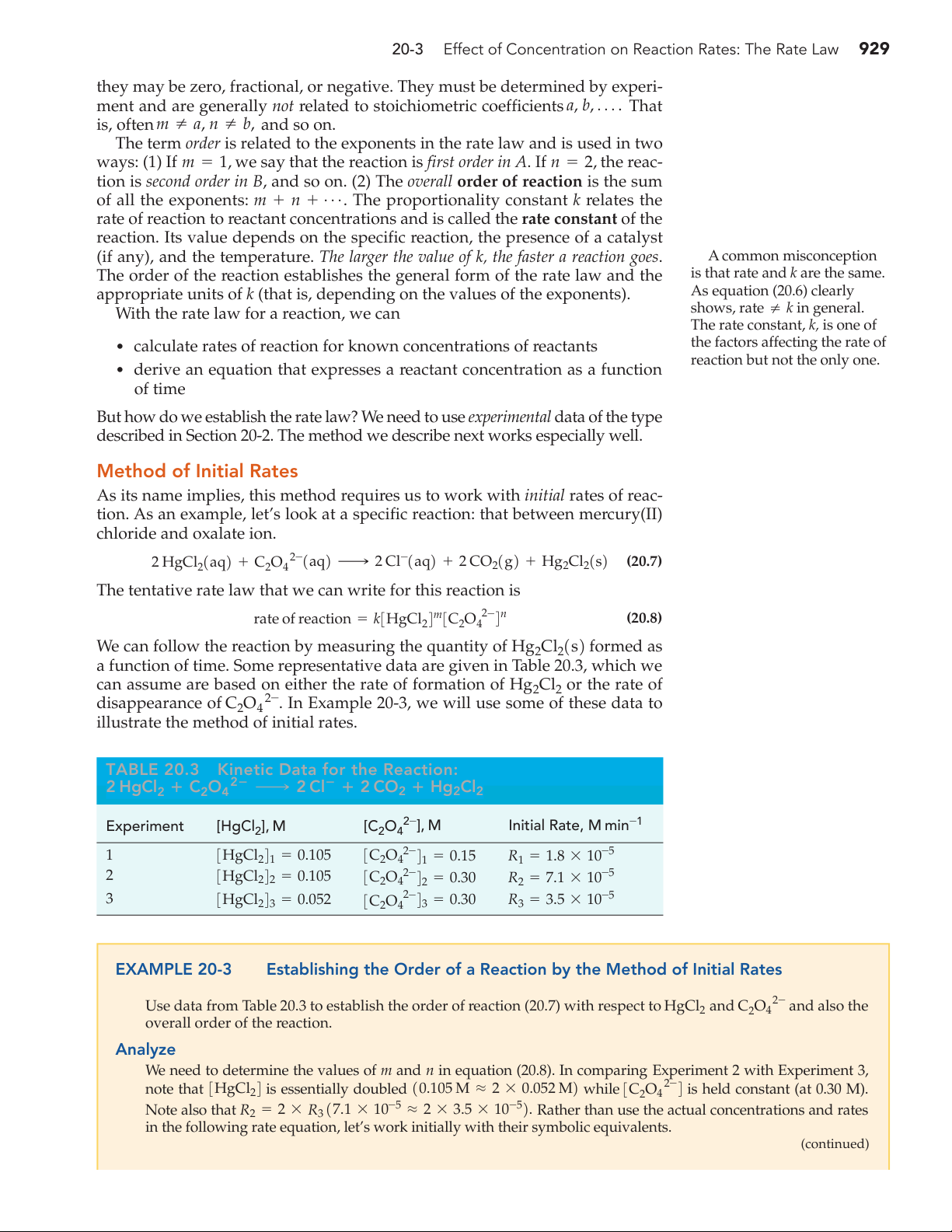
described in Section 20-2. The method we describe next works especially well. Method of Initial Rates
As its name implies, this method requires us to work with initial rates of reac-
tion. As an example, let’s look at a specific reaction: that between mercury(II) chloride and oxalate ion. 2 HgCl 2- 21aq2 + C
1aq2 ¡ 2 Cl-1aq2 + 2 CO21g2 + Hg2Cl21s2 (20.7) 2O4
The tentative rate law that we can write for this reaction is rate of reaction = k3HgCl m 2- 24 3C 4n (20.8) 2O4
We can follow the reaction by measuring the quantity of Hg2Cl21s2 formed as
a function of time. Some representative data are given in Table 20.3, which we
can assume are based on either the rate of formation of Hg2Cl2 or the rate of disappearance of C 2- 2O4 .
In Example 20-3, we will use some of these data to
illustrate the method of initial rates. TABLE 20.3 Kinetic Data for the Reaction: 2 HgCl C O 2ⴚ 2 ⴙ 2 4 ¡ 2 Clⴚ ⴙ 2 CO 2 ⴙ Hg2Cl2 Experiment [HgCl 2- 2], M [C2O4 ], M Initial Rate, M min-1 1 3HgCl 2- 241 = 0.105 3C2O4 4 1 = 0.15 R1 = 1.8 * 10-5 2 3HgCl 2- 242 = 0.105 3C2O4 4 2 = 0.30 R2 = 7.1 * 10-5 3 3HgCl 2- 243 = 0.052 3C2O4 4 3 = 0.30 R3 = 3.5 * 10-5 EXAMPLE 20-3
Establishing the Order of a Reaction by the Method of Initial Rates
Use data from Table 20.3 to establish the order of reaction (20.7) with respect to and C 2- HgCl2 2O4 and also the overall order of the reaction. Analyze
We need to determine the values of m and n in equation (20.8). In comparing Experiment 2 with Experiment 3,
note that 3HgCl24 is essentially doubled 10.105 M L 2 * 0.052 M2 while 3C 2- 2O4 4 is held constant (at 0.30 M). Note also that R 5
2 = 2 * R3 17.1 * 10-5 L 2 * 3.5 * 10- 2. Rather than use the actual concentrations and rates
in the following rate equation, let’s work initially with their symbolic equivalents. (continued) 930 Chapter 20 Chemical Kinetics Solve We begin by writing R m 2- n 2- n 2 = k * 3HgCl 4 2 2 * 3C2O 4 = k * 12 * 3HgCl24 4 4 2 32m * 3C O 2 4 3 R m 2- n 3 = k * 3HgCl 4 2 3 * 3C2O 4 4 3 2 * 2- R k * 2m * 3HgCl m 24 * 3C O 4n R2 = 3 = 2 = 3 2 4 3 = 2m R3 R3 k * 3HgCl m 2- 243 * 3C2O4 4n 3 In order that 2m = 2, m = 1.
To determine the value of n, we can form the ratio R2>R1. Now, 3C 2- 2O4 4 is doubled and 3HgCl24 is held
constant. This time, let’s use actual concentrations instead of symbolic equivalents. Also, we now have the value m = 1. R 1 2- n n 2 = k * 3HgCl 4 2 2 * 3C2O4 4 = k * 1 2 0.105 1 * 12 * 0.152 2 R 1 2- n 1 = k * 3HgCl 4 2 1 * 3C2O4 4 = k * 1 2 0.105 1 * 1 2 0.15 n 1 R 7.1 * 10-5 k * 10.10521 * 2n * 10.152n 2 = L 4 = = 2n R1 1.8 * 10-5 k * 1 2 0.105 1 * 1 2 0.15 n In order that 2n = 4, n = 2. Assess
In summary, the reaction is first order in HgCl m = 1 , second order in C 2- 2 1 2 2O4 1n = 2 2 , and third order overall 1m + n = 1 + 2 = 2
3 . In this example we found n by solving the equation 2n = 4. In some cases we may need to
solve equations containing a noninteger number, such as in 2n = 1.4143. To solve this kind of equation, we take
the logarithm of both sides, for example, log12n2 = log1 2
1.4143 , and rearrange to get n = log11.41432>log1 2 2 .
The answer is n = 0.5. Consult Appendix A-2 if you are unfamiliar with logarithms. PRACTICE EXAMPLE A:
The decomposition of N2O5 is given by the following equation: 2 N O 2 5 ¡ 4 NO2 + O2
At an initial 3N2O54 = 3.15 M, the initial rate of reaction = 5.45 * 10-5 M s-1, and when 3N2O54 = 0.78 M, the
initial rate of reaction = 1.35 * 10-5 M s-1. Determine the order of this decomposition reaction. PRACTICE EXAMPLE B:
Consider a hypothetical Experiment 4 in Table 20.3, in which the initial conditions are 3HgCl244 = 0.025 M and 3C 2- 2O4 4
4 = 0.045 M. Predict the initial rate of reaction.
We made an important observation in Example 20-3: If a reaction is first
order in one of the reactants, doubling the initial concentration of that reactant
causes the initial rate of reaction to double. Following is the general effect of
doubling the initial concentration of a particular reactant (with other reactant concentrations held constant). ▲ Reactions that are too fast
• Zero order in the reactant—there is no effect on the initial rate of reaction. for traditional methods
• First order in the reactant—the initial rate of reaction doubles. of analysis are followed by
• Second order in the reactant—the initial rate of reaction quadruples. spectroscopic methods.
• Third order in the reactant—the initial rate of reaction increases eightfold.
As previously mentioned, the order of a reaction, as indicated through the
rate law, establishes the units of the rate constant, k. That is, if on the left side
of the rate law the rate of reaction has the units M 1time2-1, on the right side,
the units of k must provide for the cancellations that also lead to M 1time2-1.
Thus, for the rate law established in Example 20-3, rate l
aw: rate of reaction = k * 3HgCl 2- 24 * 3C2O4 42 M-2 min-1 M min-1 units: M2 M
Once we have the exponents in a rate equation, we can determine the value
of the rate constant, k. To do this, all we need is the rate of reaction correspond-
ing to known initial concentrations of reactants, as illustrated in Example 20-4. 20-4 Zero-Order Reactions 931 EXAMPLE 20-4 Using the Rate Law
Use the results of Example 20-3 and data from Table 20.3 to establish the value of k in the rate law (20.8). Analyze
We can use data from any one of the three experiments of Table 20.3, together with the values m = 1 and n = 2. Solve
First, we solve equation (20.8) for k. R 1.8 * 10-5 M min-1 1 k = = 3HgCl 2- 243C2O4 42 0.105 M * 10.1522 M2 = 7.6 * 10-3 M-2 min-1 Assess
If the rate data in Table 20.3 were based on the disappearance of HgCl2 instead of C 2- 2O4 , R 1 in this setup
would be twice as great and k for the general rate of reaction would be based on -1 Note the 2 * ¢3HgCl24> ¢t.
units on the rate constant are M-2 min-1, which are appropriate units for a third-order rate constant. Checking
the units in an answer is one way to ensure that we have not made any mistakes. PRACTICE EXAMPLE A:
A reaction has the rate law: rate = k3A4 3
2 B4. When 3A4 = 1.12 M and 3B4 = 0.87 M, the
rate of reaction = 4.78 * 10-2 M s-1. What is the value of the rate constant, k? PRACTICE EXAMPLE B:
What is the rate of reaction (20.7) at the point where 3HgCl24 = 0.050 M and 3C 2- 2O4 4 = 0.025 M? 20-3 CONCEPT ASSESSMENT
The rate of decomposition of gaseous acetaldehyde, CH3CHO, to gaseous
methane and carbon monoxide is found to increase by a factor of 2.83 when the
initial concentration of acetaldehyde is doubled. What is the order of this reaction? 20-4 Zero-Order Reactions
An overall zero-order reaction has a rate law in which the sum of the expo-
nents, m + n Á, is equal to 0. As an example, let’s take a reaction in which a
single reactant A decomposes to products. A ¡ products
If the reaction is zero order, the rate law is
rate of reaction = k3A40 = k = constant (20.9)
Other features of this zero-order reaction are:
• The concentration–time graph is a straight line with a negative slope (Fig. 20-3).
• The rate of reaction, which is equal to k and remains constant throughout
the reaction, is the negative of the slope of this line.
• The units of k are the same as the units of the rate of a reaction: mol for example, mol L-1 s-1 L-1 (time)-1, or M s-1.
Equation (20.9) is the rate law for a zero-order reaction. Another useful
equation, called an integrated rate law, expresses the concentration of a
reactant as a function of time. This equation can be established rather easily 932 Chapter 20 Chemical Kinetics ▲ The dependence of k on 20-2 ARE YOU WONDERING? temperature is discussed in Section 20-9.
What is the difference between the rate and the rate constant?
Many students have difficulty with this distinction. Remember, a rate of reaction
tells how the concentration of a reactant or product changes with time and is often
expressed as moles per liter per second. A rate of reaction can be established
through an expression of the type - ¢3A4>¢t, from a tangent to a
concentration–time curve, and by calculation from a rate law. In most cases, the [A]
rate of a reaction strongly depends on reactant concentrations and, therefore, 0
changes continuously during a reaction.
The rate constant of a reaction (k) relates the rate of a reaction to reactant
concentrations. Generally, it is not itself a rate of reaction, but it can be used ]
to calculate rates of reaction. Once the value of k at a given temperature has [A
been established, this value stays fixed for the given reaction, regardless of the
reactant concentrations. The units of reaction rate do not depend on the order
of a reaction, but those of k do, as we shall see in this and the following two sections. t Time f ▲ FIGURE 20-3 A zero-order reaction: A ¡ products
from the graph in Figure 20-3. Let’s start with the general equation for a The initial concentration of straight line the reactant A is 3A4 that 0 , is, 3A4 = 3A4 at y = mx + b 0 t = 0. 3A4 decreases until the reaction
and substitute y = 3A4t (the concentration of A at some time
stops. This occurs at the time, t); x = t (time);
b = 3A40 (the initial concentration of A at time t = 0 ); and m = - k (m, the t where f , 3A4 = 0. The slope of the line is
slope of the straight line, is obtained as indicated in the caption to Figure 20-3). 10 - 3A402 3A4 = - 0 1 tf - 02 tf. The rate constant is the 3A4t = -kt + 3A40 (20.10) negative of the slope:3A40
k = - slope = tf. 20-3 ARE YOU WONDERING? ▲
Does the term “integrated” rate law have anything to do Perhaps the most important with integral calculus? examples of zero-order reac-
tions are found in the action of
Not surprisingly, it does. The rate of reaction in a rate law, such as equation (20.9), is enzymes. Enzyme-catalyzed
an instantaneous rate, which we learned in Are You Wondering 20-1 can be repre- reactions are discussed in
sented through differentials. When -d3A4>dt is substituted for the rate of reaction in Section 20-11.
the rate law for a zero-order reaction, we get the equation -d3A4>dt = k. We can
separate the differentials to obtain d3A4 = -k dt
. At this point we can apply the cal-
culus procedure of integration to obtain, successively, the following expressions.
The final one is equation (20.10), the integrated rate law for a zero-order reaction. 3A4 t t d3A4 = -k dt, 3A4t - 3A4 3A4 A L 0 = -kt, t = -kt + 3 40 3A4 L 0 0 20-5 First-Order Reactions
An overall first-order reaction has a rate law in which the sum of the expo-
nents, m + n + Á, is equal to 1. A particularly common type of first-order
reaction, and the only type we will consider, is one in which a single reactant 20-5 First-Order Reactions 933
decomposes into products. The decomposition of H2O ,2 a reaction we encoun-
tered in Section 20-2, is a first-order reaction. 1 H O 2 21aq2 ¡ H O 2 1l2 + 2 O21g2
The rate of reaction depends on the concentration of H2O2 raised to the first power, that is, rate of reaction = k3H2O24 (20.11)
It is easy to establish that the reaction is first order by the method of initial
rates, but there are also other ways of recognizing a first-order reaction.
An Integrated Rate Law for a First-Order Reaction
Let us begin our discussion of first-order reactions as we did zero-order reac-
tions, by examining a hypothetical reaction Most processes in nature ▲ A ¡ products follow first-order chemical
For a first-order reaction, the rate law is kinetics. If you had a bank that compounded interest ¢3A4 continuously, then your funds rate of reaction = - = k3A4 (20.12) ¢t would grow exponentially.
We can obtain the integrated rate law for this first-order reaction by applying
the calculus technique of integration to equation (20.12). The result of this
derivation (shown in Are You Wondering 20-4) is 3A4 ln t = -kt or ln3A4t = -kt + ln3A40 (20.13) 3A40 3A4 KEEP IN MIND
t is the concentration of A at time t, 3A40 is its concentration at t = 0, and k
is the rate constant. Because the logarithms of numbers are dimensionless that scatter of experimental
(have no units), the product -k * t must also be dimensionless. This means data on a straight-line graph
that the unit of k in a first-order reaction is such as s-1 1time2-1, or min-1.
often results in a value of k cal-
Equation (20.13) is that of a straight line. culated from equation (20.13) less reliable than a value ln3A4 = 1- A obtained from the slope t k2t + ln3 40 ¯˚˘˚˙ ¯ ˚˘˚ ˙ ¯ ˚˘˚ ˙ of the straight line. y = #
Equation of straight line m x + b 20-4 ARE YOU WONDERING?
How do we obtain the integrated rate law for a first-order reaction?
If the reaction A ¡ products is first order, then the rate law is, in differential form, d3A4>dt = -k3A4.
Separation of the differentials leads to the expression d3A4>3A4 = -k dt .
Integration of this expression between the limits 3A40 at time t = 0 and 3A4t at
time t is indicated through the expression 3A4t d3A4 t = -k dt L3A4 3A4 L 0 0
The result of the integration is equation (20.13), the integrated rate law. 3A4 ln t 3 = - A4 kt 0 934 Chapter 20 Chemical Kinetics EXAMPLE 20-5
Using the Integrated Rate Law for a First-Order Reaction H O
2 21aq2, initially at a concentration of 2.32 M, is allowed to decompose. What will 3H2O 4 2 be at t = ? 1200 s Use k = 7.30 * 10-4 1
s- for this first-order decomposition. Analyze
We have values for three of the four quantities in equation (20.13): k = 7.30 * 10-4 s-1 t = 1200 s 3H O 2 240 = 2.32 M 3H O 2 24t = ?
We need to solve for the fourth quantity. Solve
We substitute into the expression ln3H2O24t = -kt + ln3H2O240
= -17.30 * 10-4 s-1 * 1200 s2 + ln (2.32) = -0.8760 + 0.8415 = -0.0345 3H2O24t = e-0.0345 = 0.966 M Assess
This calculated value agrees well with the experimentally determined value of 0.98 M, shown below. 0.800 0.400 ▲ FIGURE 20-4
Test for a first-order reaction: ] 0.000 Decomposition of H O 2 2 21aq2 O
Plot of ln H2O2 versus t. The data are 2H
based on Table 20.1 and are listed below. 21.095 ln [ 2 0.400
The slope of the line is used in the text. t, s [H2O2] ,M ln [H2O2] 2 0.800 1500 s 0 2.32 0.842 21.095 200 2.01 0.698 Slope 5 5 2 7.30 3 1024 s21 1500 s 2 1.200 400 1.72 0.542 600 1.49 0.399 1200 0.98 -0.020 1800 0.62 -0.48 600 1200 1800 2400 3000 3000 0.25 -1.39 Time, s PRACTICE EXAMPLE A:
The reaction A ¡ 2 B + C is first order. If the initial 3A4 = 2.80 M and
k = 3.02 * 10-3 s-1, what is the value of 3A4 after 325 s? PRACTICE EXAMPLE B:
Use data tabulated in Figure 20-4, together with equation (20.13), to show that the decomposition of H O
2 2 is a first-order reaction. [Hint: Use a pair of data points for 3H O 2 4 2 0 and 3H O 2 24t and
their corresponding times to solve for k. Repeat this calculation using other sets of data. How should the results compare?] 20-5 First-Order Reactions 935
An easy test for a first-order reaction is to plot the natural logarithm of a
reactant concentration versus time and see if the graph is linear. The data from
Table 20.1 are plotted in Figure 20-4, and the rate constant k is derived from the
slope of the line: k = -slope = -1-7.30 * 10-4 - s 12 = 7.30 * 10-4 s-1. An
alternative, nongraphical approach, illustrated in Practice Example 20-5B, is to
substitute data points into equation (20.13) and solve for k.
Although until now we have used only molar concentrations in kinetics
equations, we can sometimes work directly with the masses of reactants.
Another possibility is to work with a fraction of reactant consumed, as is done in the concept of half-life.
The half-life of a reaction is the time required for one-half of a reactant to be
consumed. It is the time during which the amount of reactant or its concentra-
tion decreases to one-half of its initial value. That is, at t = t1>2, 3A4 = 1 A t 23 40.
At this time, equation (20.13) takes the form 3A4 1 A 1 ln t 23 40 = ln = ln = -ln 3 2 = - k * t A4 1>2 0 3A40 2 ln 2 0.693 t1 = (20.14) >2 = k k
Equation (20.14) is valid only for first-order reactions. We will derive half-life
expressions for other types of reactions as we encounter them.
For the decomposition of H2O21aq2, the reaction described in Section 20-2,
we conclude that the half-life is 0.693 t1>2 = = 9.49 * 102 s = 949 s 7.30 * 10-4 s-1
Equation (20.14) indicates that the half-life is constant for a first-order reaction. ▲ Half-life is constant for
Thus, regardless of the value of 3A40 at the time we begin to follow a reaction, first-order reactions but not
at t = t1>2, 3A4 = 1 A 0. After two half-lives, that is, at t = 2 * t . * constant for zero-order or 23 4 1>2 3A4 = 12 1 second-order reactions. For a A 0 = 1 A 0. At t = 3 * t 23 4 43 4 1 A 0, and so on. >2, 3A4 = 183 4 zero-order reaction, half-life
The constancy of the half-life and its independence of the initial concentra- decreases with decreasing
tion can be used as a test for a first-order reaction. Try it with the simple reactant concentration. For a
concentration–time graph of Figure 20-2. That is, starting with 3H2O24 = 2.32 M second-order reaction, half-
at t = 0, at what time is 3H2O24 equal to 1.16 M? 0.58 M? 0.29 M? Starting with life increases with decreasing 3H O
2 24 = 1.50 M at t = 600 s, at what time is 3H2O24 = 0.75 M? reactant concentration.
In the discussion above we made the assumption that the stoichiometric
coefficient a = 1. What would the rate equations look like if a Z 1? In this case we would write a A ¡ products for which the rate law is 1 ¢3A4 rate of reaction = - = k3A4 a ¢t
which can be rearranged to give ¢3A4 - = ak3A4 ¢t
The expression above is very similar to equation (20.12) except that ak has
taken the place of k in that equation. As a result, the integrated rate law
and the half-life for the reaction a A ¡ products can be obtained from
equations (20.13) and (20.14) by replacing k with ak. We obtain 0.693
ln3A4t = -akt + ln3A40 and t1>2 = ak
As illustrated in Example 20-6, a first-order reaction can also be described
in terms of the percent of a reactant consumed or remaining. 936 Chapter 20 Chemical Kinetics EXAMPLE 20-6
Expressing Fraction (or Percent) of Reactant Consumed in a First-Order Reaction
Use a value of k = 7.30 * 10-4 s-1 for the first-order decomposition of H2O21aq2 to determine the percent H O
2 2 that has decomposed in the first 500.0 s after the reaction begins. Analyze The ratio 3H O 2 24t>3H O
2 240represents the fractional part of the initial amount of H2O2 that remains unreacted at
time t. Our problem is to evaluate this ratio at t = 500.0 .
s This is done by making use of equation (20.13),
which relates the concentration at t = 0 to the concentration at some other time. Solve
Substituting into equation (20.13), 3H O 2 24 ln t -4 = - s-1 * 3 kt = - 7.30 * 10 500.0 s = -0.365 H2O 4 2 0 3H2O 24t = e-0.365 = 0.694 and 3H O 2 24t = 3 0.694 H2O 4 3H 2 0 2O 4 2 0 The fractional part of the H O
2 2 remaining is 0.694, or 69.4%. The percent of H2O2 that has decomposed is 100.0% - 69.4% = 30.6%. Assess
The integrated form of the rate law is used for determining concentrations as a function of time. The integrated
form of the rate law for first-order reactions is useful for many types of reactions and events. We will see this
equation later when we talk about radioactivity (Section 25-5). PRACTICE EXAMPLE A:
Consider the first-order reaction A ¡ products, with k = 2.95 * 10-3 s-1. What
percent of A remains after 150 s? PRACTICE EXAMPLE B:
At what time after the start of the reaction is a sample of H O 2 21aq2 two-thirds decomposed? Reactions Involving Gases
For gaseous reactions, rates are often measured in terms of gas pressures. For
the hypothetical reaction, A1g2 ¡ products, the initial partial pressure,
1PA20, and the partial pressure at some time t, 1PA2t, are related through the expression 1P ln A2t = -kt (20.15) 1PA20
To see how this equation is derived, start with the ideal gas equation written
for reactant A: PAV = nART. Note that the ratio nA>V is the same as 3A4.
So, 3A40 = 1PA20>RT and 3A4 = t
1PA2t>RT. Substitute these terms into equa-
tion (20.13), and note that the RT terms cancel in the numerator and denomi-
nator and leave the simple ratio 1PA2t>1PA20.
Di-t-butyl peroxide (DTBP) is used as a catalyst in the manufacture of
polymers. In the gaseous state, DTBP decomposes into acetone and ethane by a first-order reaction. C8H18O2(g) ¡ 2 CH C 3 OCH3(g) + CH3CH3(g) (20.16) DTBP acetone ethane
Partial pressures of DTBP are plotted as a function of time in Figure 20-5, and
the half-life of the reaction is indicated.
As shown in Are You Wondering 20-5, the partial pressure of the reactant
DTBP can be obtained from two experimentally determined quantities: the
initial pressure P0, and the total pressure Ptotal. 20-5 First-Order Reactions 937 800 700 g H m 600 , m P B T 500 D e of 400 essur t1/2 300 artial pr P 200 t1/2 100 t1/2 40 80 120 160 200 240 280 Time, min ▲ FIGURE 20-5
Decomposition of di-t-butyl peroxide (DTBP) at 147 °C
The decomposition reaction is described through equation (20.16). In this graph
of the partial pressure of DTBP as a function of time, three successive half-life
periods of 80 min each are indicated. This constancy of the half-life is proof
that the reaction is first order. 20-5 ARE YOU WONDERING?
How can the partial pressure be obtained experimentally
in a reaction involving gases?
In the study of a reaction like the decomposition of DTBP, the total pressure is typ-
ically measured as a function of time. At any time t, the total pressure is 1Ptotal2 = + + t 1PDTBP2t 1Paceton 2 e t 1Pethane2t
If the initial presure of DTBP is P , then using the stoichiometry of the balanced 0
chemical equation, the partial pressure of DTBP is PDTBP = 1P0 - Pethane2 since
for every mole of DTBP that decomposes, a mole of ethane is produced. The par-
tial pressure of acetone is Pacetone = 2 Pethane, again using the stoichiometry of the
reaction. The total pressure is then given by
Ptotal = 1P0 - Pethane2 + 2 Pethane + Pethane = P0 + 2 Pethane and P total - P0 Pethane = 2 So that
▲ Note that the total pressure 2 P in reaction (20.16) increases 0 - 1Ptotal - P02 3 P0 - Ptotal PDTBP = 1P - 0 Pethane2 = = from P0 at the start of the 2 2 reaction to 3P0 when PDTBP has fallen to zero. 938 Chapter 20 Chemical Kinetics EXAMPLE 20-7
Applying First-Order Kinetics to a Reaction Involving Gases
Reaction (20.16) is started with pure DTBP at 147 °C and 800.0 mmHg pressure in a flask of constant volume.
(a) What is the value of the rate constant k? (b) At what time will the partial pressure of DTBP be 50.0 mmHg? Analyze
In part (a) we observe from Figure 20-5 that t1>2 = 8.0 * 101 min.Recall that for a first-order reaction the
relationship between t1>2 and the rate constant is t1
>k In part (b) the final DTBP partial pressure of >2 = 0.693 .
50.0 mmHg is 1 of the starting pressure of 800.0 mmHg; that is, P 16 DTBP = 11 = mmHg. The reac- 224 * 800.0 50.0
tion must go through four half-lives. Solve
(a) Substituting in the appropriate values we have k = 0.693>t 1
1>2 = 0.693>8.0 * 10 min = 8.7 * 10-3 min-1
(b) Therefore, t = 4 * t1>2 = 4 * 8.0 * 101 min = 3.2 * 102 min. Assess
This type of analysis is useful only if we have the half-life data. If we do not, we will need to use equation (20.13). PRACTICE EXAMPLE A:
Start with DTBP at a pressure of 800.0 mmHg at 147 °C. What will be the pressure of
DTBP at t = 125 min, if t1>2 = 8.0 * 101 min? [Hint: Because 125 min is not an exact multiple of the half-life,
you must use equation (20.15). Can you see that the answer is between 200 and 400 mmHg?] PRACTICE EXAMPLE B:
Use data from Table 20.4 to determine (a) the partial pressure of ethylene oxide, and
(b) the total gas pressure after 30.0 h in a reaction vessel at 415 °C if the initial partial pressure of 1CH222O1g2 is 782 mmHg. TABLE 20.4 Some First-Order Processes Process Half-Life, t1/2 Rate Constant k, sⴚ1 Radioactive decay of 238 92 U 4.51 * 109 yr 4.87 * 10-18 Radioactive decay of 146C 5.73 * 103 yr 3.83 * 10-12 Radioactive decay of 32 15 P 14.3 d 5.61 * 10-7 Radioactive decay of 131 8.04 d 53 I 9.98 10-7 * C " 12H22O111aq2 + H O 2 1l2 15 °C C6H12O61aq2 + C6H12O61aq2 8.4 h 2.3 * 10-5 sucrose glucose fructose 1CH222O1g2 415 °C " CH 1 4 g2 + CO1g2 56.3 min 2.05 * 10-4 ethylene oxide N O " 2 51g2 in CCl4 N O 2 41g2 + 1 2 18.6 min 6.21 * 10-4 45 °C 2 O21g CH - 7 3COOH1aq2 ¡ H+1aq2 + CH C 3 OO 1aq2 8.9 * 10- s 7.8 * 105
Examples of First-Order Reactions ▲ We will explore radioactive
One of the most familiar examples of a first-order process is radioactive decay. decay in some detail in
For example, the radioactive isotope iodine-131, used in treating thyroid dis- Chapter 25.
orders, has a half-life of 8.04 days. Whatever number of iodine-131 atoms are
in a sample at a given moment, there will be half that number in 8.04 days;
one-quarter of that number in 8.04 + 8.04 = 16.08 days; and so on. The rate
constant for the decay is k = 0.693>t1
and in equation (20.13) we can use >2,
numbers of atoms, that is, Nt for 3A4t and N0 for 3A40. Table 20.4 lists several
examples of first-order processes. Note the great range of values of t1>2 and k.
The processes range from very slow to ultrafast. 20-6 Second-Order Reactions 939 20-4 CONCEPT ASSESSMENT
Without doing calculations, sketch (a) concentration versus time plots for two
first-order reactions, one having a large k and the other a small k, and (b) ln k
versus time plots for the same two situations. Describe the similarities and
differences between the two plots in each case. 20-6 Second-Order Reactions
An overall second-order reaction has a rate law with the sum of the expo-
nents, m + n Á, equal to 2. As with zero- and first-order reactions, our dis-
cussion will be limited to reactions involving the decomposition of a single reactant A ¡ products
If the reaction is second order, then we can write
rate of reaction = k3A42 (20.17)
Again, our primary interest will be in the integrated rate law that is derived
from the rate law. For the reaction we are considering, the integrated rate law is 1/[A]0 ] 1 1 = kt + [A (20.18) / A A 1 3 4t 3 40
Figure 20-6 is a plot of 1>3A4t against time. The slope of the line is k, and Time
the intercept is 1>3A40. From the graph, we can see that the units of k must be
the reciprocal of concentration divided by time: or M-11time2-1 M-1>1time2 — ▲ FIGURE 20-6 -1 -1 A straight-line plot for
for example, M s-1 or M-1 min . We can reach this same conclusion by the second-order reaction
determining the units of k that produce the required units for the rate of a A ¡ products
reaction, that is, moles per liter per unit time. From equation (20.17): The reciprocal of the concentration, 1 rate law: A 2 >3A4, is rate of reaction = k * 3 4 plotted against time. As M-1 time-1 M2 M time-1 units: the reaction proceeds, [A] decreases and 1
For the half-life of the second-order reaction A ¡ products, we can >3A4 increases in a linear fashion.
substitute t = t1>2 and 3A4 = 1 into equation (20.18). 2 3A40 The slope of the line is the rate constant k. 1 1 2 = 1 kt1>2 + ; = kt1 (20.19a) 3A4 >2 + 0>2 3A40 3A40 3A40 and 1 t1 (20.19b) >2 = k3A40
From equation (20.19a, b), we see that the half-life depends on both the rate
constant and the initial concentration 3A40. The half-life is not constant. Its
value depends on the concentration of reactant at the start of each half-life
interval. Because the starting concentration is always one-half that of the pre-
vious half-life, each successive half-life is twice as long as the one before it. 940 Chapter 20 Chemical Kinetics Pseudo-First-Order Reactions
At times, it is possible to simplify the kinetic study of complex reactions by
getting them to behave like reactions of a lower order. Then their rate laws
become easier to work with. Consider the hydrolysis of ethyl acetate, which is second order overall. CH C 3 OOCH C
2 H3 + H2O ¡ CH3COOH + CH3CH2OH Ethyl acetate Acetic acid Ethanol
Suppose we follow the hydrolysis of 1 L of aqueous 0.01 M ethyl acetate to completion. 3CH3COOCH CH 2 4
3 decreases from 0.01 M to essentially zero.
This means that 0.01 mol CH3COOCH2CH3 is consumed, and along with it,
0.01 mol H2O. Now consider what happens to the molarity of the H2O.
Initially, the solution contains about 1000 g H2O, or about 55.5 mol H2O.
When the reaction is completed, there is still 55.5 mol H2O (that is, 55.5 - 0.01 L )
55.5 . The molarity of the water remains essentially constant
throughout the reaction—55.5 M. The rate of reaction does not appear to ▲
depend on 3H2O4. So, the reaction appears to be zero order in H2O, first order The rate constant obtained
in CH3COOCH2CH3, and first order overall. A second-order reaction that is from a study that used an
made to behave like a first-order reaction by holding one reactant concentra- excess of one reactant,
tion constant is called a pseudo-first-order reaction. We can treat the reaction sometimes called Ostwald’s
with the methods of first-order reaction kinetics. Other reactions of higher isolation method after the
kineticist who invented it, is
order can be made to behave like reactions of lower order under certain con- a pseudo-rate constant and is
ditions. Thus, a third-order reaction might be converted to pseudo-second- concentration-dependent.
order or even to pseudo-first-order. 20-6 ARE YOU WONDERING?
How do we obtain the integrated rate law for the
second-order reaction A ¡ products?
In differential form, the rate law for a second-order reaction, A ¡ products, is d3A4>dt = - k3A42.
Separation of the differentials leads to the expression d3A4>3A42 = -k dt .
Integration of this expression between the limits 3A40 at time t = 0 and 3A4t at
time t is indicated through the expression 3A4t d3A4 t = - k dt L3A4 2 L 0 3A4 0
The result of the integration is equation (20.18), the integrated rate law. 1 1 1 - + = - = 3 kt or 1 kt + A4t 3A40 3A4t 3A40 20-7 Reaction Kinetics: A Summary
Let’s pause briefly to review what we have learned about rates of reaction,
rate constants, and reaction orders. Although a problem often can be solved in
several different ways, these approaches are generally most direct.
1. To calculate a rate of reaction when the rate law is known, use this expres-
sion: rate of reaction = k3A4m3B4n Á
2. To determine a rate of reaction when the rate law is not given, use
• the slope of an appropriate tangent line to the graph of 3A4 versus t
• the expression - ¢3A4>¢t, with a short time interval ¢t 20-7 Reaction Kinetics: A Summary 941 TABLE 20.5
Reaction Kinetics: A Summary for the Hypothetical Reaction a A ¡ Products Order Rate Lawa Integrated Rate Equationb Straight Line k = Units of k Half-Lifeb 0 rate = k 3A4 = - 1 A t akt + 3A40 3A4 v. time - 0 * slope mol L-1 s-1 3 4 a 2ak 1 rate = k3A4 l 3 n A4 = - A A v. time 1 s-1 0.693 t akt + ln3 40 ln3 4 - * slope a ak 1 1 1 1 2 rate = k3A42 = v. time 1 3 akt + A4 * slope L mol-1 s-1 A t 3A40 3A4 a ak3 40 ¢3A4 arate = - a 1 b a ¢t
bTo obtain the expressions for a A ¡ products, we replace k with ak in the expressions given in the text for A ¡ products.
3. To determine the order of a reaction, use one of the following methods.
• Use the method of initial rates if the experimental data are given in the
form of reaction rates at different initial concentrations.
• Find the graph of rate data that yields a straight line (Table 20.5).
• Test for the constancy of the half-life (good only for a first-order reaction).
• Substitute rate data into integrated rate laws to find the one that gives a constant value of k.
4. To find the rate constant k for a reaction, use one of the following methods.
• Obtain k from the slope of a straight-line graph.
• Substitute concentration–time data into the appropriate integrated rate law.
• Obtain k from the half-life of the reaction (good only for a first-order reaction).
5. To relate reactant concentrations and times, use the appropriate integrated
rate law after first determining k. EXAMPLE 20-8
Graphing Data to Determine the Order of a Reaction
The data listed in Table 20.6 were obtained for the decomposition reaction A ¡ products. (a) Establish the
order of the reaction. (b) What is the rate constant, k? (c) W
hat is the half-life, t1 if >2, 3A40 = 1.00 M? TABLE 20.6 Kinetic Data for Example 20-8 Time, min [A], M ln [A] 1/[A] 0 1.00 0.00 1.00 5 0.63 -0.46 1.6 10 0.46 -0.78 2.2 15 0.36 -1.02 2.8 25 0.25 -1.39 4.0 Analyze
To determine the order of the reaction, we need to plot the data according to the integrated rate law for the dif-
ferent reaction orders. The plot yielding a straight line shows the overall reaction order. Recall that the slope
of the straight line is related to the rate constant. The half-life of the reaction is also dependent on the overall reaction order. Solve
(a) Plot the following three graphs.
1. 3A4 versus time. (If a straight line, reaction is zero order.) (continued)