Giải bài tập Toán rời rạc | Đại học Nguyễn Tất Thành

lOMoAR cPSD| 46342819
GIẢI BÀI TẬP TOÁN RỜI RẠC
PHẦN I – LÝ THUYẾT TỔ HỢP................................................................................................................................................... 2
Chapter I – Nhập Môn Toán Rời Rạc (Introduce) .................................................................................................................... 2
Chapter II – Bài Toán Đếm Tổ Hợp (Counting Problem) .......................................................................................................... 5
I. NGUYÊN LÝ CỘNG VÀ NGUYÊN LÝ NHÂN ........................................................................................................................ 5
II. CHỈNH HỢP, HOÁN VỊ, TỔ HỢP ..................................................................................................................................... 13
III. NGUYÊN LÝ BÙ TRỪ ..................................................................................................................................................... 17
IV. HỆ THỨC TRUY HỒI ...................................................................................................................................................... 24
V. HÀM SINH ..................................................................................................................................................................... 41
Chapter III – Bài Toán Tồn Tại (Existence) .............................................................................................................................. 45
Chapter IV – Bài Toán Liệt Kê Tổ Hợp (Enumeration) ............................................................................................................ 47
Chapter V – Bài Toán Tối Ưu Tổ Hợp ..................................................................................................................................... 48 LÊ ĐỒ NG – ATTT-K60 1 lOMoAR cPSD| 46342819
GIẢI BÀI TẬP TOÁN RỜI RẠC
NGUYỄN ĐỨC NGHĨA
PHẦN I – LÝ THUYẾT TỔ HỢP
Chapter I – Nhập Môn Toán Rời Rạc (Introduce)
Bài 1: Cho biết trong các hệ thức dưới ây, hệ thức nào là úng hệ thức nào là sai a) A   A B
b) C     A B C
c) A   B A B
d) A     B A A B
e)  A B  \ A  B A B\ Giải a) Sai
• Xét tập 𝐴 = {1, 2} và tập 𝐵 = {2, 3}.
▪ Ta có A  B {2}
▪ Do 1   A B nên ta có A   A B
• Từ ó, Kết luận mệnh ề sai. b) Đúng
• Nếu  A        B  A B C C C  Nếu  A        B W  A B C W C C
• Từ ó, Kết luận mệnh ề úng. c) Sai
• Xét tập 𝐴 = {1, 2} và tập 𝐵 = {2, 3}.
▪ Ta có A  B {2} và A  B {1,2,3} ▪ Do {1,3}   A B nên ta có  A   B  A B .
• Từ ó, Kết luận mệnh ề sai. d) Sai
• Ta sử dụng mệnh ề A       B C  A B  A C  Ta có A           A
B  A A  A B A  A B A
• Ta có mệnh ề A   A B là sai (Câu a).
• Từ ó, Kết luận mệnh ề sai. e) Sai
• Xét tập 𝐴 = {1, 2} và tập 𝐵 = {2, 3}.
▪ Ta có A  B {1,2,3}và A  B {2}. LÊ ĐỒNG – ATTT-K60 2 lOMoAR cPSD| 46342819
▪ Ta có  A B  \ A  B {1,3} và A B\  {1}.
▪ Ta thấy  1,3    1 .
• Từ ó, Kết luận mệnh ề sai.
Bài 2: Ký hiệu ℤ là tập các số nguyên. Xét hai tập con của ℤ:
𝐴 = {𝑥 ∈ ℤ ∶ 𝑥 = 4𝑝 − 1 với một 𝑝 ∈ ℤ nào đó}.
𝐵 = {𝑦 ∈ ℤ ∶ 𝑦 = 4𝑞 − 5 với một 𝑞 ∈ ℤ nào đó}. Chứng minh rằng 𝐴 = 𝐵. Giải
Xét x A x      4 1p p
Xét y B      y 4 5q q
Ta có x    4p 14 p  1 5.
Với mỗi một giá trị của 𝑥 luôn tồn tại một giá trị 𝑞 = 𝑝 + 1 ∈ ℤ sao cho 𝑥 = 4𝑞 − 5. Từ ó ta có 𝐴 = 𝐵.
Bài 3: Xét hai tập:
A1    n :n  0 và A2    n :n  0 .
Hỏi hai tập A1 và A2 có tạo thành phân hoạch của hay không ? Nếu úng hãy giải thích câu trả lời, nếu sai, hãy
ưa ra phân hoạch úng của . Giải
• Ta có A1   A2 \  0
▪ Từ ó ta có A1 và A2 không phủ kín tập nên chúng không tạo thành một phân hoạch của tập .
• Ta có phân hoạch úng của tập như sau:
▪ Xét tập A1    n :n  0 - Tập các số nguyên âm.
▪ Xét tập A2    n :n  0 - Tập các số nguyên không âm.
▪ Từ ó ta thấy A1 và A2 phủ kín tập nên chúng tạo thành một phân hoạch của tập .
Bài 4: Cho 𝐴 = {0, 1, 2, 3, 4} và xác ịnh quan hệ ℝ trên 𝐴 bởi:
𝑅 = {(0,0); (2, 1); (0, 3); (1, 1); (3, 0); (1, 4); (4, 1); (2, 2); (2, 4); (3, 3); (4, 4); (1, 2); (4, 2)}.
Chỉ ra rằng quan hệ ℝ là quan hệ tương ương hay không ? Nếu câu trả lời là khẳng ịnh hãy ưa ra phân hoạch
của 𝐴 thành các lớp tương ương theo quan hệ ℝ ã cho. LÊ ĐỒ NG – ATTT-K60 3 lOMoAR cPSD| 46342819
Bài 5: Xét các tập với các phần tử là các số nguyên:
A0     ..., 10, 5,0,5,10,15,20,25,... ;
A1     ..., 9, 4,1,6,11,16,21,26,... ;
A2     ..., 8, 3,2,7,12,17,22,27,... ;
A3   ..., 7  , 2,3,8,13,18,23,28,... ;
A4     ..., 6, 1,4,9,14,19,24,29,... ;
a) Chỉ ra rằng các tập A0,A ,1 A A2, 3 và A4 tạo thành phân hoạch của một tập số nguyên ℤ.
b) Chỉ ra quan hệ 𝑠 tương ứng với phân hoạch này. LÊ ĐỒNG – ATTT-K60 4 lOMoAR cPSD| 46342819
Chapter II – Bài Toán Đếm Tổ Hợp (Counting Problem) I.
NGUYÊN LÝ CỘNG VÀ NGUYÊN LÝ NHÂN
Bài 1: Cho 5 ký tự 𝐴, 𝐵, 𝐶, 𝐷, 𝐸.
a) Có bao nhiêu xâu ký tự có ộ dài 4 có thể lập ược từ các ký tự ã cho (Nếu không cho phép lặp lại ký tự). Giải Ví dụ: A D E B Cách 1:
• Chọn 4 phần tử từ tập 5 phần tử {𝐴, 𝐵, 𝐶, 𝐷, 𝐸} với các ký tự không lặp lại chính là một chỉnh hợp. Theo ề
bài số cách chọn là A 4 5  120 . Cách 2:
• Gọi xâu ký tự là a a a a1 2 3 4 .Với ai   X  A B C D E, , , ,  .
▪ Số cách chọn phần tử thứ nhất a1 của xâu là: 5
▪ Số cách chọn phần tử thứ hai a2 của xâu từ tập X a\ 1là 4.
▪ Số cách chọn phần tử thứ ba a3 của xâu từ tập X \ a a1, 2 là 3.
▪ Số cách chọn phần tử thứ tư a4 của xâu từ tập X \ a a a1, 2, 3 là 2.
• Theo nguyên lý nhân thì số các xâu ký tự có thể có (Thỏa mãn yêu cầu) là: 5.4.3.2 = 𝟏𝟐𝟎.
b) Có bao nhiêu xâu ký tự trong (𝑎) bắt ầu từ 𝐵 ? Giải Ví dụ: B D E A Cách 1:
• Cố ịnh vị trí ầu tiên của xâu là ký tự 𝐵.
• Chọn 3 phẩn tử từ tập 4 phần tử còn lại {𝐴, 𝐶, 𝐷, 𝐸} với các ký tự không lặp lại chính là một chỉnh hợp.
Theo yêu cầu bài toán số cách chọn là 1. A 3 4  24. Cách 2:
• Gọi xâu ký tự là Ba a a1 2 3.Với ai   X  A C D E, , ,  .
▪ Số cách chọn phần tử thứ nhất a1 của xâu là: 4.
▪ Số cách chọn phần tử thứ hai a2 của xâu từ tập X a\ 1là 3. LÊ ĐỒ NG – ATTT-K60 5 lOMoAR cPSD| 46342819
▪ Số cách chọn phần tử thứ ba a3 của xâu từ tập X \ a a1, 2 là 2.
• Theo nguyên lý nhân thì số các xâu ký tự có thể có (Thỏa mãn yêu cầu) là: 4𝑥3𝑥2 = 𝟐𝟒.
c) Có bao nhiêu xâu ký tự trong (𝑎) không bắt ầu từ 𝐵 ?
 Số xâu ký tự mà không bắt ầu từ 𝐵 là 120 − 24 = 𝟗𝟖 (Cách).
Bài 2: Cho 𝑋 là tập 𝑛 phần tử. Có bao nhiêu bộ có thứ tự (𝐴, 𝐵) thỏa mãn A  B X ?
Bài 3: Đoàn chủ tịch của một cuộc họp gồm có 6 người: 𝐴, 𝐵, 𝐶, 𝐷, 𝐸, 𝐹 cần bầu ra “Ban lãnh ạo” gồm 1 chủ
tịch, 1 phó chủ tịch và 1 thư ký.
a) Hỏi có bao nhiêu cách khác nhau ? Giải Ví dụ: A D E
 Số cách chọn ra 3 người phân biệt từ tập 6 người là A 3 6  120.
b) Có bao nhiêu cách mà trong ó một trong hai người 𝐴, 𝐵 là chủ tịch ? Giải
• Nếu 𝐴 là chủ tịch, thì Cần chọn 2 người (1 phó chủ tịch và 1 thư ký) từ 5 người còn lại {𝐵, 𝐶, 𝐷, 𝐸, 𝐹}. Số cách chọn là A 2 5 .
• Do vai trò của 𝐴 và 𝐵 là như nhau nên số cách chọn khi 𝐴 là chủ tịch hay 𝐵 là chủ tịch là như nhau. Do ó,
Số cách thỏa mãn yêu cầu bài toán là 2.A 2 5  40 .
c) Có bao nhiêu cách chọn mà trong ó 𝐸 là một thành viên của ban lãnh ạo ? Giải Ví dụ: E D A
• Chọn vị trí trong ban lãnh ạo cho 𝐸 có 3 vị trí (chủ tịch hoặc phó chủ tịch hoặc thư ký).
• Chọn 2 người vào 2 vị trí còn lại từ tập 5 người còn lại {𝐴, 𝐵, 𝐶, 𝐷, 𝐸} có số cách là A 2 5 .
• Theo nguyên lý nhân số cách thỏa mãn yêu cầu bài toán là: 3.A 2 5  60.
d) Có bao nhiêu cách mà trong ó 𝐷 và 𝐹 là thành viên của ban lãnh ạo ? Giải Ví dụ: D F A
• Chọn 2 vị trí trong ban lãnh ạo cho 𝐷 và 𝐹. Số cách là C 2 3 .
▪ Do vai trò của 𝐷 và 𝐹 là như nhau nên chúng có thể hoán vị các chức danh cho nhau. Số cách là 2!.
• Chọn Vị trí còn lại trong ban lãnh ạo từ tập 4 người con lại {𝐴, 𝐵, 𝐶, 𝐸}. Số cách là A 1 4 . LÊ ĐỒNG – ATTT-K60 6 lOMoAR cPSD| 46342819
• Theo nguyên lý nhân, Số cách thỏa mãn yêu cầu bài toán là:  2!.C 23 .A14  24.
Bài 4: Có bao nhiêu xâu nhị phân có ộ dài 10 𝑏í𝑡 bắt ầu bởi hoặc là 101 hoặc là 111 ? Giải Ví dụ: 1 0 1 1 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 1
• Xâu nhị phân (Chỉ gồm bít 0 và 1) bắt ầu bởi 101.
▪ Ba vị trí ầu của xâu là 101 nên xâu 10 𝑏í𝑡 còn lại 10 − 3 = 7 𝑏í𝑡.
▪ Do mỗi ô trong 7 ô ó ều có 2 cách chọn (chọn 0 hoặc chọn 1) nên theo nguyên lý nhân, Số cách chọn là 27 .
• Xâu nhị phân (Chỉ gồm bít 0 và 1) bắt ầu bởi 111.
▪ Ba vị trí ầu của xâu là 111 nên xâu 10 𝑏í𝑡 còn lại 10 − 3 = 7 𝑏í𝑡.
▪ Do mỗi ô trong 6 ô ó ều có 2 cách chọn (chọn 0 hoặc chọn 1) nên theo nguyên lý nhân, Số cách chọn là 27 .
• Theo nguyên lý cộng, Số xâu nhị phân thỏa yêu cầu là: 27    27 28 256.
Bài 5: Có 10 𝑐𝑢ố𝑛 𝑠á𝑐ℎ khác nhau, trong ó có 5 𝑐𝑢ố𝑛 sách thuộc lĩnh vực 𝑇𝑖𝑛 𝐻ọ𝑐, 3 𝑐𝑢ố𝑛 sách thuộc lĩnh vực
𝑇𝑜á𝑛 𝐻ọ𝑐 và 2 𝑐𝑢ố𝑛 sách về lĩnh vực 𝑁𝑔ℎệ 𝑇ℎ𝑢ậ𝑡. Hỏi có bao nhiêu cách chọn ra 2 𝑐𝑢ố𝑛 sách có nội dung
thuộc các lĩnh vưc khác nhau từ 10 𝑐𝑢ố𝑛 sách nói trên ? Giải
• Chọn 2 cuốn sách (1 cuốn 𝑇𝑖𝑛 𝐻ọ𝑐 và 1 cuốn 𝑇𝑜á𝑛 𝐻ọ𝑐)
▪ Chọn 1 cuốn 𝑇𝑖𝑛 𝐻ọ𝑐 từ tập 5 cuốn sách 𝑇𝑖𝑛 𝐻ọ𝑐, có số cách là C 1 3 .
▪ Chọn 1 cuốn 𝑇𝑜á𝑛 𝐻ọ𝑐 từ tập 3 cuốn sách 𝑇𝑜á𝑛 𝐻ọ𝑐, có số cách là C 1 3 .
▪ Theo nguyên lý nhân, Số cách chọn là C C 1 1 5 . 3  15 .
• Chọn 2 cuốn sách (1 cuốn 𝑇𝑜á𝑛 𝐻ọ𝑐 và 1 cuốn 𝑁𝑔ℎệ 𝑇ℎ𝑢ậ𝑡)
▪ Chọn 1 cuốn 𝑇𝑜á𝑛 𝐻ọ𝑐 từ tập 3 cuốn sách 𝑇𝑜á𝑛 𝐻ọ𝑐, có số cách là C 1 3 .
▪ Chọn 1 cuốn 𝑁𝑔ℎệ 𝑇ℎ𝑢ậ𝑡 từ tập 2 cuốn sách 𝑁𝑔ℎệ 𝑇ℎ𝑢ậ𝑡, có số cách là C 1 2 .
▪ Theo nguyên lý nhân, Số cách chọn là C 1 3 .C12  6.
• Chọn 2 cuốn sách (1 cuốn Nghệ Thuật và 1 cuốn 𝑇𝑖𝑛 𝐻ọ𝑐)
▪ Chọn 1 cuốn 𝑁𝑔ℎệ 𝑇ℎ𝑢ậ𝑡 từ tập 2 cuốn sách 𝑁𝑔ℎệ 𝑇ℎ𝑢ậ𝑡, có số cách là C 1 2 .
▪ Chọn 1 cuốn 𝑇𝑖𝑛 𝐻ọ𝑐 từ tập 5 cuốn sách 𝑇𝑖𝑛 𝐻ọ𝑐, có số cách là C 1 5 .
▪ Theo nguyên lý nhân, Số cách chọn là C C 1 1 2 . 5  10.
• Theo nguyên lý cộng, Số cách chọn thỏa yêu cầu là: 15 + 6 + 10 = 𝟑𝟏. LÊ ĐỒ NG – ATTT-K60 7 lOMoAR cPSD| 46342819
Bài 6: Có 10 𝑐𝑢ố𝑛 𝑠á𝑐ℎ khác nhau, trong ó có 5 𝑐𝑢ố𝑛 sách thuộc lĩnh vực: 𝑇𝑖𝑛 𝐻ọ𝑐, 3 𝑐𝑢ố𝑛 sách thuộc lĩnh
vực 𝑇𝑜á𝑛 𝐻ọ𝑐 và 2 𝑐𝑢ố𝑛 sách về lĩnh vực 𝑁𝑔ℎệ 𝑇ℎ𝑢ậ𝑡.
a) Hỏi có bao nhiêu cách xếp 10 𝑐𝑢ố𝑛 sách này lên giá Giải
• Khi xếp lên giá thì 10 𝑐𝑢ố𝑛 sách là như nhau, nên chúng có thể ổi chỗ cho nhau ược.
• Số cách chính là số hoán vị của 10 𝑝ℎầ𝑛 𝑡ử hay 𝟏𝟎!.
b) Hỏi có bao nhiêu cách xếp 10 𝑐𝑢ố𝑛 sách này lên 1 giá sách sao cho tất cả các cuốn sách 𝑇𝑖𝑛 𝐻ọ𝑐 ược
xếp ở phía trái giá sách còn 2 cuốn sách về 𝑁𝑔ℎệ 𝑇ℎ𝑢ậ𝑡 ược xếp bên phải ? Giải Ví dụ: Tin Tin Tin Tin Tin Toán Toán
Toán Nghệ Thuật Nghệ Thuật
• Do vai trò của 5 𝑐𝑢ố𝑛 sách 𝑇𝑖𝑛 𝐻ọ𝑐 là như nhau nên chúng có thể hoán vị cho nhau. Số cách xếp 5 𝑐𝑢ố𝑛
sách 𝑇𝑖𝑛 𝐻ọ𝑐 ở bên trái là 5!.
• Do vai trò của 2 𝑐𝑢ó𝑛 sách 𝑁𝑔ℎệ 𝑇ℎ𝑢ậ𝑡 là như nhau nên chúng có thể hoán vị cho nhau. Số cách xếp 2
𝑐𝑢ó𝑛 sách 𝑁𝑔ℎệ 𝑇ℎ𝑢ậ𝑡 ở bên phải là 2!.
• Do chỉ có 10 vị trí, nhưng xếp bên trái 5 vị trí cho 𝑇𝑜á𝑛 𝐻ọ𝑐, bên phải 2 vị trí cho 𝑁𝑔ℎệ 𝑇ℎ𝑢ậ𝑡 nên còn
lại 3 𝑐𝑢ố𝑛 sách 𝑇𝑜á𝑛 𝐻ọ𝑐 sẽ tự ặt vào giữa giá sách. ▪ Số cách xếp 3 𝑐𝑢ố𝑛 sách 𝑇𝑜á𝑛 𝐻ọ𝑐 là: 3!.
• Theo nguyên lý nhân, Số cách phân chia công viêc thỏa mãn yêu cầu của bài toán là 5! .3! .2! = 𝟏𝟒𝟒𝟎.
c) Hỏi có bao nhiêu cách xếp 10 𝑐𝑢ố𝑛 sách này lên 1 giá sách sao cho tất cả các cuốn sách thuộc cùng lĩnh
vực ược xếp cạnh nhau ? Giải Ví dụ: Tin Tin Tin Tin Tin Toán Toán Toán
Nghệ Thuật Nghệ Thuật
• Coi 5 𝑐𝑢ố𝑛 sách 𝑇𝑖𝑛 𝐻ọ𝑐 là phần tử 𝑋.
▪ Số cách xếp 5 𝑐𝑢ố𝑛 sách 𝑇𝑖𝑛 𝐻ọ𝑐 trong 𝑋 là 5!.
• Coi 3 𝑐𝑢ố𝑛 sách 𝑇𝑜á𝑛 𝐻ọ𝑐 là phần tử 𝑌.
▪ Số cách xếp 3 𝑐𝑢ố𝑛 sách 𝑇𝑜á𝑛 𝐻ọ𝑐 trong 𝑌 là 3!.
• Coi 2 𝑐𝑢ố𝑛 sách 𝑁𝑔ℎệ 𝑇ℎ𝑢ậ𝑡 là phần tử 𝑍.
▪ Số cách xếp 2 𝑐𝑢ố𝑛 sách 𝑁𝑔ℎệ 𝑇ℎ𝑢ậ𝑡 trong 𝑍 là 2!.
• Số cách xếp 𝑋, 𝑌, 𝑍 vào 3 vị trí là 3!.
• Theo nguyên lý nhân, Số cách xếp thỏa mãn yêu cầu bài toán là (5! .3! .2!). 3! = 𝟖𝟔𝟒𝟎.
d) Hỏi có bao nhiêu cách xếp 10 𝑐𝑢ố𝑛 sách này lên 1 giá sách sao cho 2 𝑐𝑢ố𝑛 sách 𝑁𝑔ℎệ 𝑇ℎ𝑢ậ𝑡 không ược xếp cạnh nhau. LÊ ĐỒNG – ATTT-K60 8 lOMoAR cPSD| 46342819 Giải Ví dụ: Tin Toán Tin Toán Tin Tin Toán Tin
Nghệ Thuật Nghệ Thuật
• Ta xếp 10 𝑐𝑢ố𝑛 sách lên giá sao cho 2 𝑐𝑢ố𝑛 sách 𝑁𝑔ℎệ 𝑇ℎ𝑢ậ𝑡 luôn ược xếp cạnh nhau.
▪ Coi 2 𝑐𝑢ố𝑛 sách 𝑁𝑔ℎệ 𝑇ℎ𝑢ậ𝑡 là phần tử 𝑋.
Số cách xếp 2 𝑐𝑢ố𝑛 sách 𝑁𝑔ℎệ 𝑇ℎ𝑢ậ𝑡 trong 𝑋 là 2!.
▪ Xếp 8 𝑐𝑢ố𝑛 sách còn lại (5 𝑐𝑢ố𝑛 sách 𝑇𝑖𝑛 𝐻ọ𝑐 và 3 𝑐𝑢ố𝑛 sách 𝑇𝑜á𝑛 𝐻ọ𝑐) cùng với 𝑋 vào 9 𝑣ị 𝑡𝑟í.
Số cách xếp chúng là 9!.
▪ Theo nguyên lý nhân, Số cách xếp thỏa mãn là 2! .9!
• Ta có số cách xếp 10 𝑐𝑢ố𝑛 sách vào 1 giá là 10!.
• Theo nguyên lý bù trừ, Số cách xếp thỏa mãn yêu cầu bài toán là: 10! − 2! .9! = 𝟐𝟗𝟎𝟑𝟎𝟒𝟎.
Bài 7: Có bao nhiêu số có 4 𝑐ℎứ 𝑠ố có thể tạo thành từ các chữ số 0, 1, 2, 3, 4, 5 thỏa mãn
a) Không có chữ số nào ược lặp lại. Giải Ví dụ 1 0 2 3 Cách 1:
• Gọi số cần tìm là aaaa1 2 3 4 , trong ó ai  a j và a1  0. Có ai   X  0,1,2,3,4,5 ▪ Do a1  0 nên
a1  1,2,3,4,5 . Số cách chọn a1là 5.
▪ Do không có chữ số nào ược lặp lại nên ta cần lấy ra 3 𝑐ℎữ 𝑠ố cho a a a2, 3, 4 từ tập gồm 5 chữ số X \  a 3
1 . Số cách chọn là A5 .
• Theo nguyên lý nhân, Số các số thỏa mãn yêu cầu bài toán là 5.A 3 5  3 00 . Cách 2:
• Gọi số cần tìm là a a a a1 2 3 4 , trong ó ai  a j và a1  0. Có ai   X  0,1,2,3,4,5 .
• Số các số có 4 𝑐ℎữ 𝑠ố tạo thành từ 6 𝑐ℎữ 𝑠ố của tập X   0,1,2,3,4,5 là A 4 6 .
• Số các số có 4 𝑐ℎữ 𝑠ố mà bắt ầu bằng chữ số 0. ▪ Ví dụ 0 1 2 3 LÊ ĐỒ NG – ATTT-K60 9 lOMoAR cPSD| 46342819
▪ Do số tạo thành không có chữ số nào ươc lặp lại nên ta cần lấy ra 3 𝑐ℎữ 𝑠ố cho a2,a ,3 a4 từ tập gồm 5
chữ số X \ 0  . Số cách chọn là A 35.
• Do các số mà bắt ầu bằng chữ số 0 là các số vô nghĩa.Nên Theo nguyên lý bù trừ, Số các số thỏa mãn yêu
cầu bài toán là: A 4 3 6   A5 300 .
b) Các chữ số ược lặp lại. Giải
• Gọi số cần tìm là aaaa1 2 3 4 , trong ó a1  0. Có ai   X  0,1,2,3,4,5 .
▪ Do a1  0 nên a1  1,2,3,4,5 . Số cách chọn a1là 5.
▪ Do các chữ số có thể ược lặp lại, nên mỗi chữ số a a2, 3,a4ều có 6 cách chọn từ tập 𝑋.Do ó, số cách
chọn bộ  a a2, 3,a4 là 63.
• Theo nguyên lý nhân, số các số thỏa mãn yêu cầu bài toán là 5.63  1080 . c) Các số chẵn trong (𝑏). Giải
• Gọi số cần tìm là aaaa1 2 3 4 , trong ó a1  0. Có ai   X  0,1,2,3,4,5 .
• Do số cần tìm là chẵn nên a4   0,2,4 . Số cách chọn a4là 3.
▪ Do a1  0 nên a1  1,2,3,4,5 . Số cách chọn a1là 5.
▪ Do các chữ số có thể ược lặp lại, nên mỗi chữ số a a2, 3ều có 6 cách chọn từ tập 𝑋. Do ó, số cách chọn
bộ  a a2, 3 là 62 .
• Theo nguyên lý nhân, Số các số thỏa mãn yêu cầu bài toán là: 5.6 .32  540.
d) Các số chẵn mà các chữ số của nó không ược lặp lại. Giải
• Gọi số cần tìm là aaaa1 2 3 4 , trong ó ai  a j và a1  0. Có ai   X  0,1,2,3,4,5 .
• Do số cần tìm là chẵn nên a4   0,2,4 . • Nếu a4  0
▪ Do số tạo thành không có chữ số nào ươc lặp lại nên ta cần lấy ra 3 𝑐ℎữ 𝑠ố cho a1,a ,2 a3 từ tập gồm 5
chữ số X \ 0  . Số cách chọn là A 35.
▪ Theo nguyên lý nhân, Số các số trong 3
trường hợp này là: 1.A5 . LÊ ĐỒNG – ATTT-K60 10 lOMoAR cPSD| 46342819
• Nếu a4   2,4
▪ Số cách chọn a4 là 2.
▪ Do a1  0 nên a1 X \ 0, a4 . Số cách chọn a1là 4.
▪ Do không có chữ số nào ược lặp lại nên ta cần lấy ra 2 𝑐ℎữ 𝑠ố cho a a2, 3 từ tập gồm 4 chữ số X \ a a 2
1, 4 . Số cách chọn là A4 .
▪ Theo nguyên lý nhân, Số các số trong trường hợp này là: 4.A 2 4 .2  96
• Theo nguyên lý cộng, Số các số thỏa mãn yêu cầu bài toán là: A 3 5   96 156.
Bài 8: Trên cạnh bên của một tam giác ta lấy 𝑛 iểm, trên cạnh bên thứ hai lấy 𝑚 iểm. Mỗi một trong hai ỉnh của
cạnh áy ược nối với các iểm ược chọn trên cạnh bên ối diện bởi các ường thẳng. Hỏi
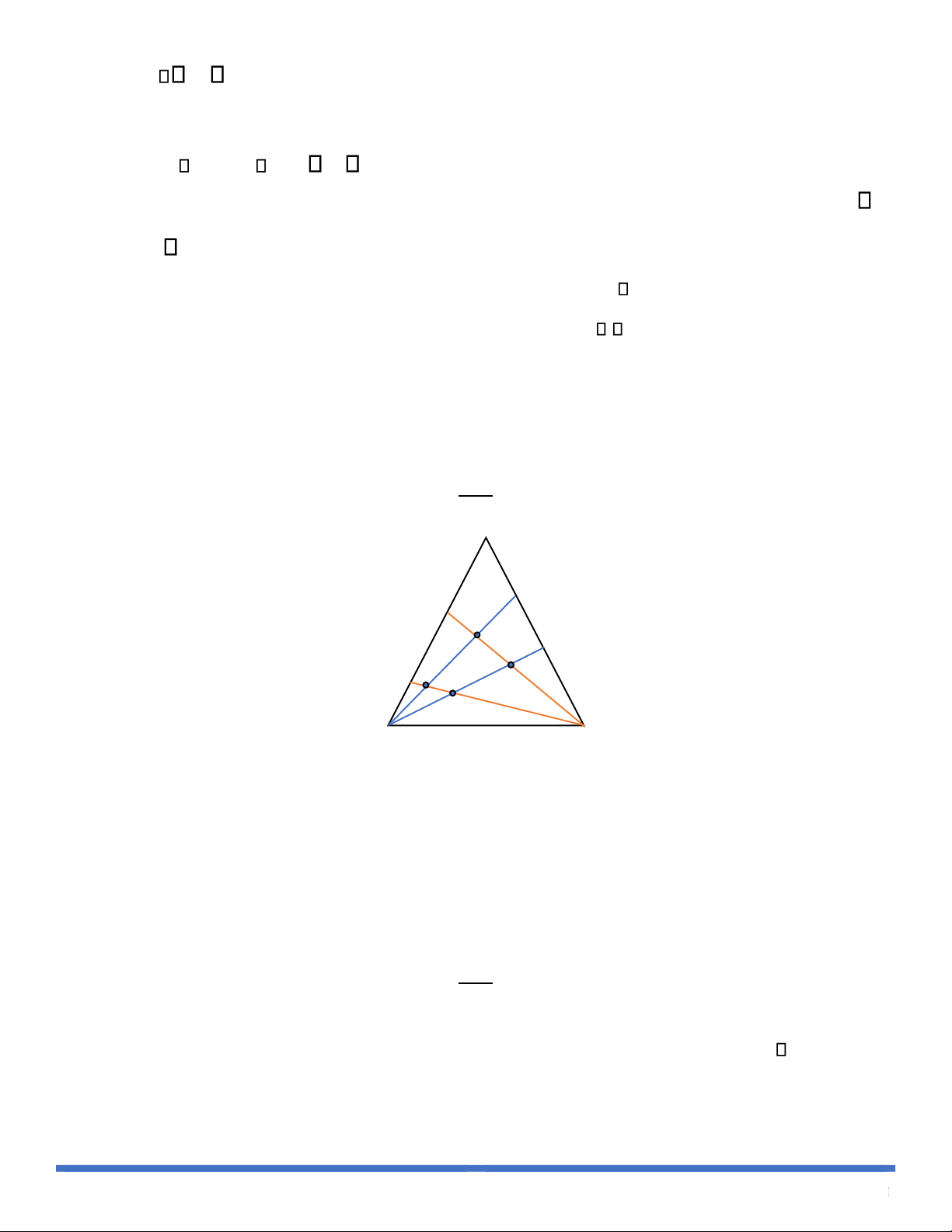
a) Có bao nhiêu giao iểm của các ường thẳng nằm trong a giác Giải A m iểm n iểm B C
• Giả sử các ỉnh ở áy là 𝐵 và 𝐶. Trên cạnh 𝐴𝐵 lấy 𝑚 iểm. Trên cạnh 𝐴𝐶 lấy 𝑛 iểm.
• Nối iểm 𝐵 với 𝑛 iểm trên cạnh 𝐴𝐶 ta ược 𝑛 ường thẳng.
• Nối iểm 𝐶 vứi 𝑚 iểm trên cạnh 𝐴𝐵 ta ược 𝑚 ường thẳng.
▪ Mỗi ường i qua 𝐶 không song song với bất kỳ ường nào trong 𝑛 ường kia sẽ cắt 𝑛 ường kia tại 𝑛 giao iểm nằm trong tam giác.
▪ Do có tất cả 𝑚 ường i qua 𝐶, nên số giao iểm nằm trong tam giác là 𝒏. 𝒎
b) Các ường thẳng chia tam giác ra làm bao nhiêu phần Giải
• Kẻ 𝑚 ường thẳng qua iểm 𝐶 sẽ chia ∆𝐴𝐵𝐶 ra thành 𝑚 + 1 phần.
• Ta thấy 𝑛 ường thẳng qua 𝐵 chia một phần (Trong 𝑚 + 1 phần) ra thành 𝑛 + 1 phần nhỏ.  Do có tất cả
𝑚 + 1 phần nên tam giác sẽ ược chia ra làm: (𝒎 + 𝟏). (𝒏 + 𝟏) phần. LÊ ĐỒ NG – ATTT-K60 11 lOMoAR cPSD| 46342819
Bài 9: Một cán bộ tin học do ãng trí ã quên mật khẩu của phần mềm máy tính của mình. May mắn là anh ta còn
nhớ mật khẩu có dạng 𝑁𝑁𝑁 − 𝑋𝑋 trong ó 𝑁𝑁𝑁 là các chữ số, còn 𝑋𝑋 là các chữ cái lấy trong bảng chữ cái có
26 𝑐ℎữ. Hỏi trong trường hợp xấu nhất cần phải thử bao nhiêu mật khẩu ể có thể tìm lại mật khẩu ã ặt ? Giải Ví dụ 0 1 0 A A
• Ta có tập các chữ số có 10 𝑝ℎầ𝑛 𝑡ử là  0,1,2,3,4,5,6,7,8,9
• Ta có tập các chữ cái có 26 𝑝ℎầ𝑛 𝑡ử.
• Mật khẩu có chứa 3 𝑐ℎữ 𝑠ố 𝑁𝑁𝑁 (có thể lặp lại)
▪ Mỗi chữ số 𝑁 trong mật khẩu có 10 cách chọn từ tập  0,1,2,3,4,5,6,7,8,9 .
▪ Theo nguyên lý nhân, Số cách chọn cho 𝑁𝑁𝑁 là 103 .
• Mật khẩu có chứa 2 𝑐ℎữ 𝑐á𝑖 𝑋𝑋 (có thể lặp lại) ▪ Mỗi chữ cái 𝑋 trong mật khẩu có 26 cách chọn.
▪ Theo nguyên lý nhân, Số cách chọn cho 𝑋𝑋 là 262 .
• Số trường hợp xấu nhất cần phải thử cũng chính là số lượng mật khẩu có thể có. Số mật khẩu có thể có ó là 10 .263 2 .
Bài 10: Hỏi có bao nhiêu bộ có thứ tự gồm 3 tập X1, X2, X3 thỏa mãn
X1   X2
X3  1,2,3,4,5,6,7,8 và X1  X2  X3  
Ví dụ hai bộ: X1   1,2,3 , X2   1,4,8 , X3   2,5,6,7 và X1   1,4,8 , X2   1,2,3 , X3   2,5,6,7 ược coi là khác nhau. Giải
• Do X1  X2  X3   nên một phần tử ai chỉ thuộc tối a là 1 tập hợp  Xét một phần tử ai 
   X1 X2 X3  1,2,3,4,5,6,7,8 bất kỳ
▪ Nếu ai chỉ thuộc 1 tập thì nó có 3 cách chọn (Hoặc là X1, hoặc là X2 , hoặc là X3 ) ▪ Nếu ai thuộc 2 tập hợp thì có C 2
3 cách chọn vị trí cho ai .
▪ Nếu ai  X j với j  1,2,3 thì vô lý. Do aj  X1 X2  X3.
▪ Theo nguyên lý cộng, Số cách xếp chỗ cho a 2
j là 3 C3  6.
• Do a j có thể là một trong 8 số  1,2,...,7,8 nên số bộ có thứ tự  X X1, 2, X3 là 68  1679616. LÊ ĐỒNG – ATTT-K60 12 lOMoAR cPSD| 46342819 II.
CHỈNH HỢP, HOÁN VỊ, TỔ HỢP
Bài 11: Có bao nhiêu hoán vị của các chữ cái trong xâu 𝐴𝐵𝐶𝐷𝐸𝐹 mà trong ó có chứa xâu con 𝐷𝐸𝐹 ? Giải
• Coi xâu con 𝐷𝐸𝐹 là phần tử 𝑋.
• Xếp 𝐴𝐵𝐶𝑋 vào 4 vị trí, số các hoán vị có thể có là 4!.
• Số các hoán vị chứa xâu con 𝐷𝐸𝐹 chính là số các hoán vị của xâu 𝐴𝐵𝐶𝑋. Số các hoán vị thỏa mãn yêu
cầu bài toán là 4! = 𝟐𝟒.
Bài 12: Có bao nhiêu hoán vị của các chữ cái trong xâu 𝐴𝐵𝐶𝐷𝐸𝐹 mà trong ó có chứa ba chữ cái 𝐷, 𝐸, 𝐹 ứng cạnh nhau ? Giải
• Coi ba chữ cái 𝐷, 𝐸, 𝐹 ứng cạnh nhau là phần tử 𝑋.
▪ Do vai trò của 𝐷, 𝐸, 𝐹 như nhau nên số các cách xếp có thể có của 𝑋 là 3!.
• Xếp 𝐴, 𝐵, 𝐶, 𝑋 vào 4 vị trí, số các hoán vị có thể có là 4!.
• Theo nguyên lý nhân, Số các hoán vị thỏa mãn yêu cầu bài toán là 3! .4! = 𝟏𝟒𝟒.
Bài 13: Có bao nhiêu cách xếp 6 𝑛𝑔ườ𝑖 vào ngồi quanh cái bàn tròn (hai cách xếp không coi là khác nhau nếu
chúng có thể thu ược từ nhau bởi phép quay bàn tròn) ? Giải
Ví dụ: Xét cách xếp 3 người 𝐴, 𝐵, 𝐶 quanh một bàn tròn như sau ược coi là một. A C B C B A C B A Cách 1:
• Xếp 6 𝑛𝑔ườ𝑖 ngồi quanh một cái bàn thì số cách xếp là 6!.
• Xếp quanh một bàn tròn
▪ Khi ta quay bàn tròn thì với một cách xếp có thứ tự của 6 người sẽ ược tính 6 lần.
• Từ ó, số cách xếp 6 𝑛𝑔ườ𝑖 ngồi quanh một bàn tròn là  5! 1 02 . Cách 2:
• Cố ịnh một vị trí ở trên bàn. LÊ ĐỒ NG – ATTT-K60 13 lOMoAR cPSD| 46342819
• Do có 6 𝑛𝑔ườ𝑖 mà có một người ngồi cố ịnh nên số cách sắp xếp người ngồi quanh bàn tròn là một bộ
hoán vị của 5 𝑛𝑔ườ𝑖 còn lại.
• Từ ó, Số cách xếp 6 𝑛𝑔ườ𝑖 ngồi quanh một bàn tròn là 5! = 𝟏𝟐𝟎. Tổng Quát:
• Số cách xếp 𝑛 người ngồi thành một hang ngang là 𝒏!.
• Số cách xếp 𝑛 người ngồi quanh một bàn tròn là (𝒏 − 𝟏)!.
Bài 14: Có bao nhiêu cách xếp 7 học sinh 𝑛𝑎𝑚 và 5 học sinh 𝑛ữ ra thành một hàng ngang sao cho không có 2
nữ sinh nào ứng cạnh nhau ? Giải
• Ký hiệu 𝑁𝑎𝑚 là 𝐵, còn 𝑁ữ là 𝐺.  Ví dụ B G B G B G B G B B B G
• Xếp chỗ cho 7 bạn 𝑁𝑎𝑚
▪ Do các bạn 𝑁𝑎𝑚 có thể hoán vị cho nhau nên số cách xếp 𝑁𝑎𝑚 là 7!.
• Do có 7 bạn 𝑁𝑎𝑚 nên giữa chúng hình thành lên 6 𝑘ℎ𝑒 + 2 𝑏ê𝑛 = 8 𝑣ị 𝑡𝑟í. Ta có thể xếp 5 bạn 𝑁ữ vào
8 vị trí trên sao cho không có í𝑡 𝑛ℎấ𝑡 2 bạn 𝑁ữ ở cùng một vị trí thì sẽ thỏa mãn yêu cầu bài toán.
▪ Số cách xếp 5 bạn 𝑁ữ vào 8 𝑣ị 𝑡𝑟í mà không có í𝑡 𝑛ℎấ𝑡 2 bạn 𝑁ữ ở cùng một vị trí chính là một
chỉnh hợp chập 8 của 5. Số cách xếp là A 5 8 .
• Theo nguyên lý nhân, Số cách xếp thỏa mãn yêu cầu bài toán là 7!.A 5 8  33868800.
Bài 15: Có bao nhiêu xâu nhị phân ộ dài 32 𝑏𝑖𝑡 mà trong ó có úng 6 𝑠ố 1 ? Giải Ví dụ 1 … 1 1 … 1 … 1 … 1
• Xâu nhị phân chỉ gồm 2 số là 0 hoặc 1.
• Xâu nhị phân có ộ dài 32 𝑏í𝑡 có úng 6 𝑠ố 1 chính là số cách chọn ra 6 𝑣ị 𝑡𝑟í từ 32 𝑣ị 𝑡𝑟í ể xếp số 1 vào ▪
Số cách chọn ó là C 6 32  906192.
Bài 16: Có bao nhiêu xâu ký tự có thể tạo ược từ các chữ cái 𝑴𝑰𝑺𝑺𝑰𝑺𝑺𝑰𝑷𝑷𝑰 ? Giải Ví dụ: M I S S I S S I P P I Cách 1:
• Xâu ký tự trên gồm 11 chữ cái có số lượng các chữ cái là ▪ Có 1 chữ 𝑀. ▪ Có 4 chữ 𝐼. ▪ Có 4 chữ 𝑆. LÊ ĐỒNG – ATTT-K60 14 lOMoAR cPSD| 46342819 ▪ Có 2 chữ 𝑃.
• Xếp 11 ký tự thành một hàng ta ược số xâu là 11!.  Do có 4 chữ 𝐼, có 4 chữ 𝑆, có 2 chữ 𝑃 ược lặp lại.
▪ Từ ó, Số xâu ký tự có thể tạo thành từ các ký tự trên là:  34650. Cách 2:
• Chọn 4 vị trí từ 11 vị trí ể xếp 4 chữ 𝐼. Số cách chọn là C 4 11 .
▪ Sau khi chọn xong 4 vị trí cho chữ 𝐼, còn lại 11 − 4 = 7 vị trí.
• Chọn 4 vị trí từ 7 vị trí còn lại ể xếp 4 chữ 𝑆. Số cách chọn là C 4 7 .
▪ Sau khi chọn xong 4 vị trí cho chữ 𝑆, còn lại 7 − 4 = 3 vị trí.
• Chọn 2 vị trí từ 3 vị trí còn lại ể xếp 2 chữ 𝑃. Số cách chọn là C 2 3 .
▪ Sau khi chọn xong 2 vị trí cho chữ 𝑃, còn lại 3 − 2 = 1 vị trí.  Ví trí còn lại sẽ dành cho chữ 𝑀.
• Theo nguyên lý nhân, Số các xâu ký tự thỏa mãn là: C C C 4 2 11 7 . 4. 3 .1 34650. Tổng Quát:
• Xếp 𝑛 ồ vật lại thành một hàng ngang.
• Trong 𝑛 ồ vật ó có n1ồ vật loại 𝐼, …, có nk ồ vật loại 𝑘.
• Số cách xếp ồ thỏa mãn là:
n! . n1!.n2!...nk !
Bài 17: Có 8 cuốn sách khác nhau. Hỏi có bao nhiêu các phân các cuốn sách này cho 3 học sinh: 𝑀ơ, 𝑀𝑎𝑖, 𝑀ậ𝑛
sao cho 𝑀ơ nhận ược 4 cuốn sách, còn 𝑀𝑎𝑖, 𝑀ậ𝑛 mỗi người nhận ược 2 cuốn sách ? Giải
• 𝑀ơ có 4 cuốn sách từ 8 cuốn sách. Số cách lấy sách cho 𝑀ơ là C 4 8 .
• 𝑀𝑎𝑖 có 2 cuốn sách từ 4 cuốn sách còn lại. Số cách lấy sách cho 𝑀𝑎𝑖 là C 2 4 .
• 𝑀ậ𝑛 có 2 cuốn sách từ 2 cuốn sách còn lại. Số cách lấy sách cho 𝑀ậ𝑛 là 1.
• Theo nguyên lý nhân, Số cách lấy sách thỏa mãn yêu càu bài toán là: C C 4 2 8 . 4  420 .
Bài 18: Giả sử 𝑋 là tập có 𝑡 phần tử. Ta gọi 𝑡ổ ℎợ𝑝 𝑙ặ𝑝 chập 𝑘 từ 𝑡 phần tử của 𝑋 là một bộ không có thứ tự
gồm 𝑘 thành phần lấy từ các phần tử của 𝑋. Ví dụ
• Xét tập 𝑋 = {𝑎, 𝑏, 𝑐}. Các tổ hợp lặp chập 2 từ các phần tử của 𝑋 là ▪ (𝑎, 𝑎); (𝑎, 𝑏); (𝑎, 𝑐); (𝑏, 𝑏); (𝑏, 𝑐); (𝑐, 𝑐).
Chứng minh rằng số tổ hợp lặp chập 𝑘 từ 𝑡 là:C t 1 k
k t   1  Ck t   1. LÊ ĐỒ NG – ATTT-K60 15 lOMoAR cPSD| 46342819 Giải
• Ta xếp 𝑡 phần tử thành một hàng ngang.
▪ Giữa 2 phần tử liên tiếp luôn tồn tại 1 vách ngăn.
▪ Do có 𝑡 phần tử nên sẽ có 𝑡 − 1 vách ngăn.
▪ Chúng sẽ tạo thành 𝑡 ngăn ược ánh số từ 1 tới 𝑡.
• Xét tổ hợp lặp chập 𝑘 của 𝑡 phần tử.
▪ Coi 𝑘 phần tử chính là 𝑘 ngôi sao. Xếp 𝑘 ngôi sao thành một hàng ngang.
▪ Ngăn thứ 𝒊 chứa thêm một ngôi sao mỗi lần khi phần tử thứ 𝒊 của tập xuất hiện trong tổ hợp.
• Ví dụ tổ hợp lặp chập 𝟔 của 𝟒 phần tử (𝒂, 𝒃, 𝒄, 𝒅) ược biểu thị bởi 6 𝑛𝑔ô𝑖 𝑠𝑎𝑜 và 3 vách ngăn.
▪ Biểu thị tổ hợp chứa úng 2 phần tử thứ nhất, 1 phần tử thứ hai, không có phần tử thứ ba, có 3 phần tử
thứ tư của tập hợp. Hay (𝑎, 𝑎, 𝑏, 𝑑, 𝑑, 𝑑) * * * * * *
▪ Biểu thị tổ hợp chứa úng 1 phần tử thứ hai, 5 phần tử thứ tư của tập hợp. Hay (𝑏, 𝑑, 𝑑, 𝑑, 𝑑, 𝑑) * * * * * *
• Ta thấy một dãy chứa (𝑡 − 1) vách ngăn và 𝑘 ngôi sao ứng với một tổ hợp lặp chập 𝑘 của 𝑡 phần tử.
▪ Chọn 𝑡 − 1 vị trí từ 𝑡 − 1 + 𝑘 vị trí ể xếp chỗ cho 𝑡 − 1 vách ngăn. Số cách xếp là: C t  1 t   1 k .
▪ Còn lại 𝑘 vị trí trong dãy ứng với 𝑘 ngôi sao.
• Vậy số các tổ hợp lặp chập 𝑘 từ 𝑡 phần tử là C t  1 t   1 k .
• Theo tính chất của tổ hợp C k n k t  1 k n  Cn
, ta có Ct   1 k  Ct  1 k .
Bài 19: Có 3 rổ ựng các quả cầu 𝑋𝑎𝑛ℎ, Đỏ, 𝑇í𝑚. Mỗi giỏ chỉ chứa các quả cầu cùng màu và mỗi giỏ chứa ít ra là 8 quả cầu.
a) Có bao nhiêu cách chọn ra 8 quả cầu. Giải
• Gọi số quả cầu lấy ra ở mỗi giỏ lần lượt là x x x1, 2, 3.
• Số cách lấy ra 8 quả cầu từ ba giỏ chính là số nghiệm nguyên không âm của phương trình sau
x1  x2  x3  8
• Số nghiệm nguyên không âm của phương trình trên chính là số tổ hợp lặp chập 8 của 3 phần tử. Số tổ
hợp lặp ó là C3 8 18   C102  45
b) Có bao nhiêu cách chọn ra 8 quả cầu mà trong ó có ít nhất một quả cầu Đỏ, một quả cầu 𝑋𝑎𝑛ℎ, một quả cầu 𝑇í𝑚 ? LÊ ĐỒNG – ATTT-K60 16 lOMoAR cPSD| 46342819 Giải
• Gọi số quả cầu lấy ra ở mỗi giỏ lần lượt là x x x1, 2, 3.
• Số cách lấy ra 8 quả cầu từ ba giỏ chính là số nghiệm nguyên không âm của phương trình sau
x1  x2  x3  8
 Đặt t1   x1 1, t2  x2  1, t3  x3  1.
▪ Do lấy ra ít nhất một quả cầu Đỏ, một quả cầu 𝑋𝑎𝑛ℎ, một quả cầu 𝑇í𝑚 nên x1  1, x2  1, x3  1 ▪ Do
vậy t1  0, t2  0, t3  0.
• Phương trình ầu bài trở thành t1    t2 t3 5(*).
• Số cách chọn ra 8 quả cầu mà trong ó có ít nhất một quả cầu Đỏ, một quả cầu 𝑋𝑎𝑛ℎ, một quả cầu 𝑇í𝑚
chính là số nghiệm nguyên không âm của phương trình (*). Nó chính là số tổ hợp lặp chập 5 của 3 phần
tử. Số tổ hợp ó là C 5 2
3 5 1     C7 21
Bài 20: Xét phương trình x1  x2  x3  x4  29.
a) Hỏi phương trình ã cho có bao nhiêu nghiệm nguyên dương ? Giải
• Do x1,...,x4  1 (Nguyên dương). Ta ặt yi    xi 1
yi  0 với   i 1,4
• Phương trình ầu bài trở thành y1  y2  y3  y4  25 (*) có nghiệm nguyên không âm.
• Mỗi nghiệm của phương trình (*) tương ứng với việc chọn 25 phần tử từ bốn loại ▪ Gồm y1 giá trị loại I.
▪ Gồm y2 giá trị loại II.
▪ Gồm y3 giá trị loại III.
▪ Gồm y4 giá trị loại IV.
• Từ ó, Số nghiệm của phương trình (*) chính là số tổ hợp lặp chập 25 của 4 phần tử. Số tổ hợp lặp ó là
C42 525 1  C238
b) Hỏi phương trình ã cho có bao nhiêu nghiệm nguyên không âm ? Giải
 Số nghiệm không âm của phương trình chính là số tổ hợp lặp chập 29 của 4 phần tử. Số tổ hợp lặp ó là
C42 929 1  C332 III. NGUYÊN LÝ BÙ TRỪ
Bài 1: Hỏi trong oạn từ 1 ến 1000 có bao nhiêu số hoặc là số lẻ, hoặc là số chính phương ? LÊ ĐỒ NG – ATTT-K60 17 lOMoAR cPSD| 46342819 Giải
• Gọi 𝐴 là tập hợp các số lẻ.
• Gọi 𝐵 là tập hợp các số chính phương.
▪ Khi ó, A B là tập hợp các số chính phương lẻ.
▪ Khi ó, A B là tập hợp các số lẻ hoặc là số chính phương.
• Tập hợp các số lẻ là các số không chia hết cho 2. ▪ Tập hợp các số chẵn là các số chia hết cho 2.
▪ Trong oạn từ 1 ến 1000, Số các số chẵn là  1000    2    500.
▪ Do trong oạn từ 1 ến 1000 chỉ gồm các số là chẵn hoặc lẻ, nên Số các số lẻ trong oạn này là 1000
500 500  . Từ ó có A  500.
• Một số ược gọi là Số chính phương nếu nó ược viết dưới dạng k  2 trong ó k  .
▪ Do ó, Số các số chính phương trong oạn từ 1 ến 1000 chính là số các giá trị 𝑘 nguyên dương có ược
thỏa mãn 1  k2 1000.
▪ Số giá trị 𝑘 thỏa mãn là   1000   31. Từ ó ta có B  31.
• Ta sẽ tìm số các Số chính phương lẻ trong oạn từ 1 ến 1000.
▪ Số các số chính phương lẻ trong oạn từ 1 ến 1000 chính là số các giá trị 𝑘 nguyên dương có ược thỏa
mãn 1  2k 1 2  1000   0 k 15. Từ ó ta có k  0,1,...,15 .
▪ Từ ó ta có A  B15.
• Theo nguyên lý bù trừ, Trong oạn từ 1 ến 1000 có số các số hoặc là số lẻ, hoặc là số chính phương là
A      B A B A B 500   31 16 515 số.
Bài 2: Có bao nhiêu xâu nhị phân ộ dài 8, không chứa 6 số 0 liên tiếp ? Giải
• Xâu nhị phân là xâu chỉ gồm các số 0 và 1.
• Số các xâu nhị phân có ộ dài 8 𝑏í𝑡 là 28  256.
• Ta ếm số xâu nhị phân có ộ dài 8 𝑏í𝑡, gồm 6 số 0 liên tiếp. ▪ Ta ếm số xâu nhị phân có úng 6 số 0 liên tiếp.
Ta coi 6 số 0 liên tiếp là một số 0*.
Nếu 0* ở ầu, ta xét xâu bắt ầu bởi 0*1 → Bít cuối cùng có thể là 0 hoặc 1. Số xâu là: 1.21  2.
Nếu 0* ở cuối, ta xét xâu kết thúc bởi 10* → Bít ầu tiên có thể là 0 hoặc 1. Số xâu là: 1.21  2.
Nếu 0* ở giữa, ta xét xâu có chứa 10*1 → Do xâu có ộ dài là 8 nên Số xâu là: 1.
Vậy tổng số xâu nhị phân có ược trong trường hợp này là 2 + 2 + 1 = 𝟓.
▪ Ta ếm số xâu nhị phân có úng 7 số 0 liên tiếp. LÊ ĐỒNG – ATTT-K60 18 lOMoAR cPSD| 46342819
Ta coi 7 số 0 liên tiếp là một số 0*.
Nếu 0* ở ầu, ta xét xâu bắt ầu bởi 0*1. Do xâu có ộ dài 8 𝑏í𝑡 nên Số xâu là: 1.
Nếu 0* ở cuối, ta xét xâu kết thúc bởi 10*. Do xâu có ộ dài 8 𝑏í𝑡 nên Số xâu là: 1.
Vậy tổng số xâu nhị phân có ược trong trường hợp này là 1 + 1 = 𝟐. ▪ Ta ếm số xâu nhị
phân có úng 8 số 0 liên tiếp.
Do xâu có ộ dài là 8 𝑏í𝑡 nên Số xâu nhị phân có úng 8 số 0 liên tiếp là 1.
▪ Vậy số xâu nhị phân có chứa 6 số 0 liên tiếp là: 5 + 2 + 1 = 𝟖.
• Theo nguyên lý bù trừ, Số xâu nhị phân ộ dài 8 không chứa 6 số 0 liên tiếp là 28   8 2 84 .
Bài 3: Có bao nhiêu số có 10 chữ số với các chữ số 1, 2, 3 mà trong ó mỗi chữ số 1, 2, 3 có mặt ít nhất 1 lần. Giải
• Gọi Ai là tập các số có 10 chữ số mà chữ số 𝑖 không xuất hiện. Với (𝑖 = 1, 2, 3). ▪
Ta có A1  A2  A3 là tập các số có 10 chữ số mà chữ số 1 hoặc chữ số 2 hoặc chữ số 3 không xuất hiện.
• Số các số tự nhiên có 10 chữ số có thể có từ tập 1, 2, 3 là 310 .
• Số các số tự nhiên có 10 chữ số mà trong ó mỗi chữ số 1, 2, 3 xuất hiện ít nhất 1 lần ▪ Theo nguyên lý
bù trừ, ta có N=310    A1 A2 A3 .
• Ta có N1    A1 A2 A3 ▪
A1 - Tập các số có 10 chữ số mà chữ số 1 không xuất hiện.
Các số có 10 chữ số trong trường hợp này chỉ từ các chữ số 2, 3.
Số các số trong trường hợp này là 210.Do ó ta có A1  210. ▪
Tương tự ta có A1  A2  A3  210. ▪ Do ó N1  3.210 .
• Ta có N2       A1 A2 A2 A3 A3 A1 . ▪
A A1 2 - Tập các số có 10 chữ số mà chữ số 1 và 2 không xuất hiện.
Các số có 10 chữ số trong trường hợp này chỉ từ các chữ số 1.
Số các số trong trường hợp này là 1. Do ó A1   A21. ▪
Tương tự ta có A1      A2 A2 A3 A3 A1 1. ▪ Do ó N2  3.
• Ta có N3    A1 A2 A3 LÊ ĐỒ NG – ATTT-K60 19 lOMoAR cPSD| 46342819 ▪
A1  A2 A3 - Tập các số có 10 chữ số mà chữ số 1, 2, 3 không xuất hiện. ▪
Do tập các chữ số có 10 chữ số ược tạo thành từ các chữ số 1, 2, 3 nên N3     A1 A2 A30. LÊ ĐỒNG – ATTT-K60 20