GIẢI TÍCH 1 - Đề Cuối Kỳ Giai Tích 1 các năm gần đây. Môn Giải tích 1 (GT01) | Trường Đại học Giao thông Vận tải.

lOMoAR cPSD| 58833082
TÀI LIỆU TỔNG HỢP BÀI TẬP MÔN GIẢI TÍCH 1 NẰM TRONG ĐỀ THI
CUỐI KỲ CÁC NĂM GẦN ĐÂY VÀ LỜI GIẢI MỘT SỐ BÀI MẪU.
I) Chương 1: Giới hạn và tính liên tục của dãy số DẠNG 1: TÍNH LIM ex   x x2  cos x
Bài 1: (Đề K64) Tính I  limx 0 (x sin )cosx x Ta có ex   x x2  cos x I  limx 0 x vsin x 1 ex   x x2  cos x =limx 0 .limx 0 cos x x sin x ex   x x2  cos x =limx 0 x sin x   0 ex   12x sin x
Sử dụng L’Hopital     limx 0  0  1 cosx x e   2 cosx sin x ex  sin x =limx 0 =limx 0  1 cos x
Chú ý: Cứ dạng ta đạo hàm đến bao giờ hết dạng thì thôi
Bài 2 (Đề K62) I  lim sinn n  1 sin  n   Ta có: 1 lOMoAR cPSD| 58833082
TÀI LIỆU TỔNG HỢP BÀI TẬP MÔN GIẢI TÍCH 1 NẰM TRONG ĐỀ THI
CUỐI KỲ CÁC NĂM GẦN ĐÂY VÀ LỜI GIẢI MỘT SỐ BÀI MẪU. n  1 n  n   1 1 .0 n n 1 n n 0 n n .0 0 n n 1 2 2 2017   limcos
Bài 3 (Đề K62) limn   2017x2  2   Ta có: 2.2017x2  2017x  2  I  lim    1 3 2     x   2017x  2      2 2 lOMoAR cPSD| 58833082
TÀI LIỆU TỔNG HỢP BÀI TẬP MÔN GIẢI TÍCH 1 NẰM TRONG ĐỀ THI
CUỐI KỲ CÁC NĂM GẦN ĐÂY VÀ LỜI GIẢI MỘT SỐ BÀI MẪU. 2 2 2 lim =ex   lim x   2017 =e x2 =e3
CÁC BÀI TẬP CÒN LẠI SẼ ĐƯỢC CHỮA TRỰC TIẾP TẠI CLB THAM GIA
GROUP: “Góc Học Tập ĐHXD” để nhận tài liệu và thông tin về lớp chữa đề Bài 4: (K63) Tính lim  x  n n n6    3 2 n6  2n3  cos2x cos3x Bài 5: (K62) TínhI x  limx 0 2
Bài 6. (K64) Cho dãy số xn  n 2n   1 sin ;n n N * Bài 7. (K63) Tính lim n n  2016n  1 1 2 Bài 8. (K64) Tính I  lim 0 4 2 4 n 1 Bài 9. (K63) Tính lim  n  x  ln(1 x) Bài 10 (K63) Tính lim x 0 3 lOMoAR cPSD| 58833082
TÀI LIỆU TỔNG HỢP BÀI TẬP MÔN GIẢI TÍCH 1 NẰM TRONG ĐỀ THI
CUỐI KỲ CÁC NĂM GẦN ĐÂY VÀ LỜI GIẢI MỘT SỐ BÀI MẪU. Bài 11: (K63) Tính I=?; I  lim n Bài 12: (K64) Cho 2 n dãy số x  n Bài 13 (K62) Tính I  lim 2016   1 n 2 n n
arctan x  sin x x.ln(1 2x ) Bài 14 (K62) Tìm giới hạn I  lim Bài 15 (K64) Tính lim 2 1 5 x 0
Bài 16 (K63). Tính I  lim x 0 sin3x ln(1 x) arctan x Bài 17 (K64). Tính 2 lim 1 1 Bài 18 (K62) Tính 2 lim x  4
Bài 19 (K61) Tínhlimx 1   ln x  x  1  x100  2x 1   0 Bài 20 (K63) I  limx 1
x50  2x 1     0 phương án đạo hàm tử và mẫu
DẠNG 2: CÁCH TÌM CỰC TRị HÀM SỐ DỰA VÀO DẤU f   ( )x BÀI TẬP
* Bài toán tìm cực trị Hàm số 4 lOMoAR cPSD| 58833082
TÀI LIỆU TỔNG HỢP BÀI TẬP MÔN GIẢI TÍCH 1 NẰM TRONG ĐỀ THI
CUỐI KỲ CÁC NĂM GẦN ĐÂY VÀ LỜI GIẢI MỘT SỐ BÀI MẪU.
Câu 1 (K64) Tìm cực trị của hàm số y  x e4. 4x
Ta có: y  x e4. 4x TXĐ: D=R
 y  2 .x e4x  4.e4x.x2 =e4x(4x2  2 )x
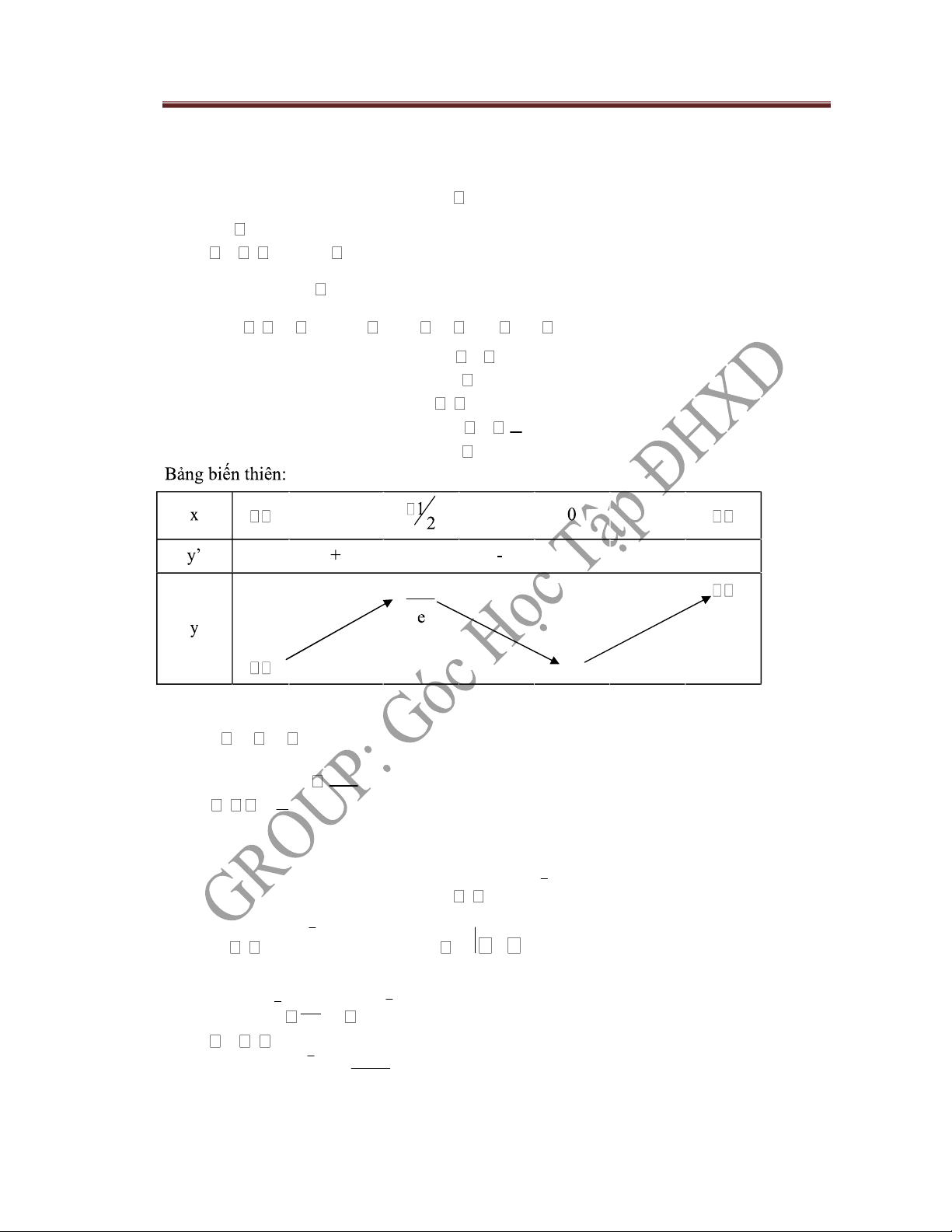
y  0  e4x(4x2  2 )x  0  4x2  2x  0  x  0    1  x   2 0 0 1 2 4 0 Vậy yct  0  x  0 1 1 yct  2    x 4e 2 1
Câu 2 (K64) Tìm cực trị của hàm số y   (x 2)ex 1 Ta có: y   (x 2)ex TXĐ: D  R  0 1 1 x  12 (x  2).ex  y  e x 1 5 lOMoAR cPSD| 58833082
TÀI LIỆU TỔNG HỢP BÀI TẬP MÔN GIẢI TÍCH 1 NẰM TRONG ĐỀ THI
CUỐI KỲ CÁC NĂM GẦN ĐÂY VÀ LỜI GIẢI MỘT SỐ BÀI MẪU.
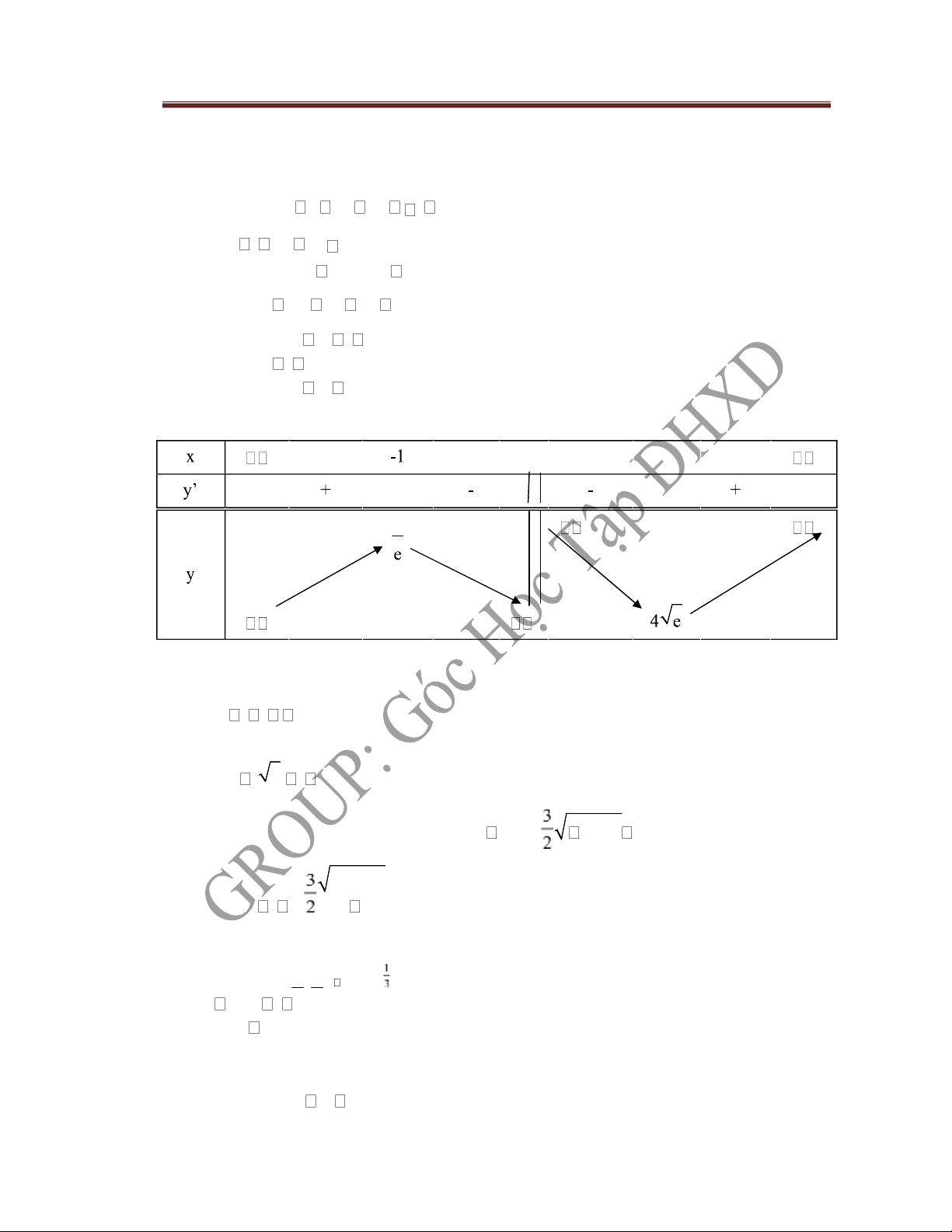
x  1 x  22    0 y  0  e   x   x2  x  2  0  x   1    x  2 Bảng biến thiên 0 2 0 0 1 1 Vậy yCÑ     x 1 e yct  4 e   x 2
Câu 3 (K64) Tìm cực trị của hàm số f x( )   x3 (x  1)2
Ta có: f x( )   x 3 (x  1)2 TXĐ: D=R 3 2  f  ( )x   1 . .(x  1) 2 3 1 =1+ x  1 3 6 lOMoAR cPSD| 58833082
TÀI LIỆU TỔNG HỢP BÀI TẬP MÔN GIẢI TÍCH 1 NẰM TRONG ĐỀ THI
CUỐI KỲ CÁC NĂM GẦN ĐÂY VÀ LỜI GIẢI MỘT SỐ BÀI MẪU. x  1
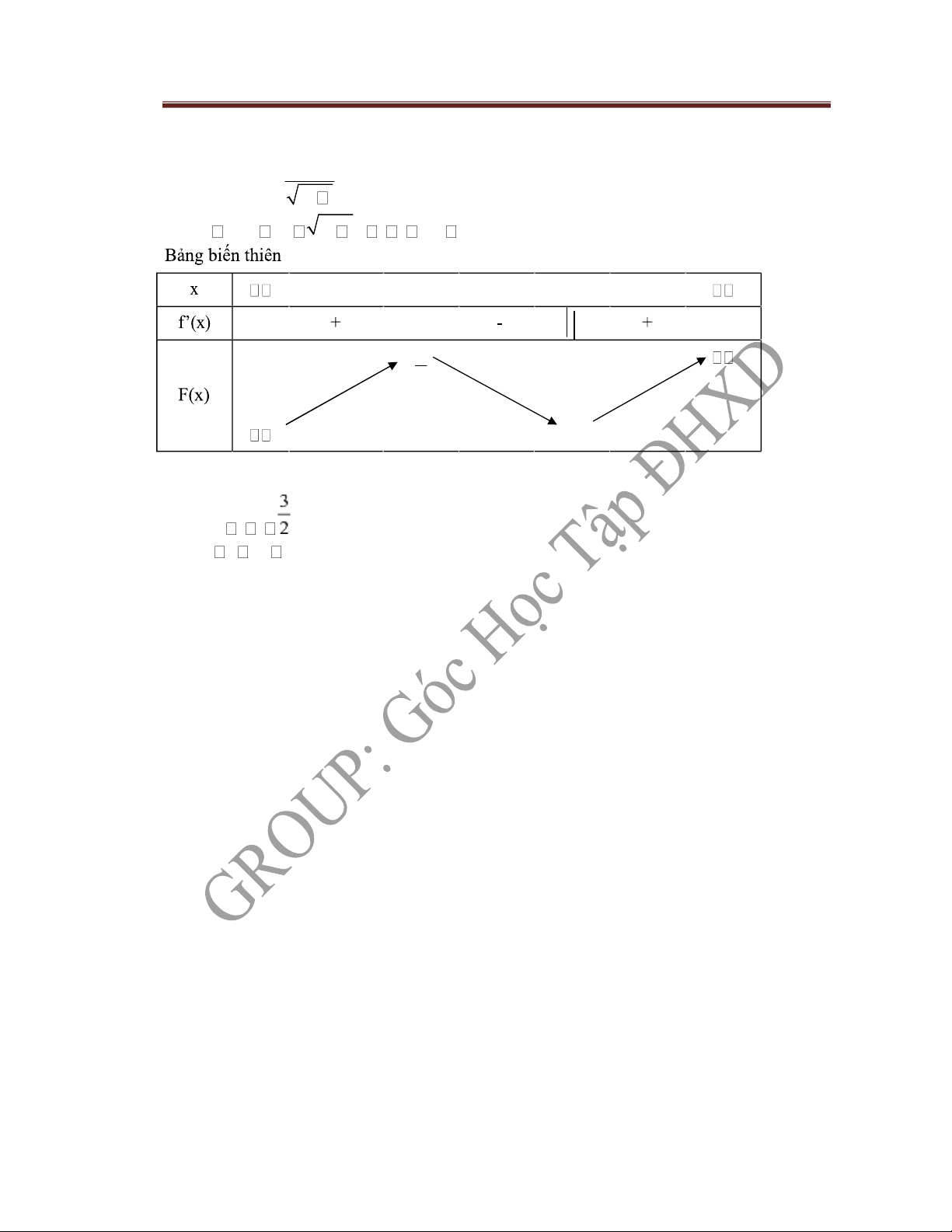
f  ( )x  0  3 x  1    1x  0 0 1 0 3 2 1
Vậy fCÑ    x 0 fct  1 x  1 7 lOMoAR cPSD| 58833082
TÀI LIỆU TỔNG HỢP BÀI TẬP MÔN GIẢI TÍCH 1 NẰM TRONG ĐỀ THI
CUỐI KỲ CÁC NĂM GẦN ĐÂY VÀ LỜI GIẢI MỘT SỐ BÀI MẪU.
CÁC BÀI TẬP CÒN LẠI SẼ ĐƯỢC CHỮA TRỰC TIẾP TẠI CLB
THAM GIA GROUP: “Góc Học Tập ĐHXD” để nhận tài liệu và thông tin về lớp chữa đề
Câu 4 (K63) Tìm cực trị của hàm số y  x2.e6x
Câu 5 (K64) Tìm cực trị của hàm số y   (x 6)e 2 3
Câu 6 (K64) Tìm cực trị của hàm số y   x ln(1 sin )x  x Câu 7 (K63) Tính limx 0 x e( x  1) ln(1 sin )x  x Câu 8 (K63) Tính lim x 0 xtan x x  arctan x Câu 9 (K64) Tính lim 3 x 0 x sin x  xe. x Câu 10 (K64) Tính lim x 0 xln(1 2 )x cos x e x x Câu 11 (K63) Tính lim x 0 xln(1 2 )x sin x  xcosx
Câu 12 (K64) Tính giới hạn limx 0 x.ln(1 3x2 ) x xe.  ln(1 x) lim
Câu 13 (K62) Tính giới hạn 2 x 0 x lOMoAR cPSD| 58833082
TÀI LIỆU TỔNG HỢP BÀI TẬP MÔN GIẢI TÍCH 1 NẰM TRONG ĐỀ THI
CUỐI KỲ CÁC NĂM GẦN ĐÂY VÀ LỜI GIẢI MỘT SỐ BÀI MẪU. 6
Dạng 3: Bài toán xét tính liên tục trên R Bài 1 (K62):  x  sin x  , neu x  0 Cho hàm số f x( )   x
Chứng minh hàm số liên tục tại x 0   0 , neu x  0 Ta có: x  sin x 1 cosx +) lim  lim  0 x 0 x x 0 1 x  sin x 1 cos x +) lim  lim  0 x 0 x x 0 1 +) f (0)  0
Vậy lim f x( )  lim f x( )  f (0)  0 nên hàm số liên tục trên R. x 0 x 0 Bài 2(K63):
Xác định a, b để các hàm sau liên tục trên R.
 ax2  bx  1, neu x ? 0 F x( )  
 acosx  bsin , neu x x  0 9 lOMoAR cPSD| 58833082
TÀI LIỆU TỔNG HỢP BÀI TẬP MÔN GIẢI TÍCH 1 NẰM TRONG ĐỀ THI
CUỐI KỲ CÁC NĂM GẦN ĐÂY VÀ LỜI GIẢI MỘT SỐ BÀI MẪU. Ta có:
+) lim f x( )  lim(ax2    bx 1) 1 x 0 x 0
+) lim f x( )  lim( cosax  bsin )x  a x 0 x 0 +) f (0)  1
Vậy hàm số liên tục trên R thì:
lim f x( )  lim f x( )  f (0)  0 x 0 x 0  a=1 và b thuộc R
Bài 3(K62):Tìm a để g x( )liên tục trên R  1  x.sin , neu x  0 g x( ) x   a , neu x  0 1 1
Ta có: lim f x( )  lim .sinx  lim 0.sin  0 x 0 x 0 x x 0 x 1 1 Vì   1 sin   1 0.sin  0 x x 1 +) lim f x( )  lim .sinx  0 x 0 x 0 x +) f (0)  a
Vậy để hàm số liên tục trên R thì a=0
CÁC BÀI TẬP CÒN LẠI SẼ ĐƯỢC CHỮA TRỰC TIẾP TẠI CLB
THAM GIA GROUP: “Góc Học Tập ĐHXD” để nhận tài liệu và thông tin về lớp chữa đề 10 lOMoAR cPSD| 58833082
TÀI LIỆU TỔNG HỢP BÀI TẬP MÔN GIẢI TÍCH 1 NẰM TRONG ĐỀ THI
CUỐI KỲ CÁC NĂM GẦN ĐÂY VÀ LỜI GIẢI MỘT SỐ BÀI MẪU.  1  2017x.sin khi x  0
Bài 4(K62): CMR f x( )   2017x   0 khi x  0 Bài 5(K61):Tìm a để hàm  ln(1 sin 2017 )2 x  khi x  0 f x( )   x liên tục trên R   a2 khi x  0
Bài 6(K61):Xác định  để hàm   1  x .sin neu x  0 f x( )   x liên tục tại x 0   0 neu x  0 Bài 7(K62):CMR  1  2017x sin khi x  0 f x( )   2017x liên tục tại x 0   0 khi x  0
Chương 2: Hàm số khả vi, khai triển Maclaurin, đạo hàm, đồ thị, Viết pttp.
1) Dạng 1: Hàm số khả vi (Hay tính đọa hàm f  (x0 )) 11 lOMoAR cPSD| 58833082
TÀI LIỆU TỔNG HỢP BÀI TẬP MÔN GIẢI TÍCH 1 NẰM TRONG ĐỀ THI
CUỐI KỲ CÁC NĂM GẦN ĐÂY VÀ LỜI GIẢI MỘT SỐ BÀI MẪU.
Bài 1 (K63): Xác định a, b để hàm số:  sin x a neu x  0 0 F x( )   Khả vi tại x  bx neu x ? 0 Ta có: - Xét tính liên tục: +) lim f x( )  lim bx  0   x 0 x 0 +) lim
f x( )  lim (sin x  a)  a   x 0 x 0
+) f (0)  0 => Để hàm số liên tục a 0 - Xét tính khả vi: f x( )  f x( 0) sin x  0 +) lim   lim   1 x 0 x 0 x  0 x  0 f x( )  f x( 0) bx  0 +) lim   lim   b x 0 x 0 x  0 x  0
Để hàm số khả vi thì b  1. Vậy a  0,b  1 Bài 2 (K62):  x sin x  ; x  0 f x( )   x
CMR: hàm số liên tục tại x 0 và tính f  (0)  ?   0 ; x  0 Ta có: x  sin x 1 cosx +) lim   lim  lim  0 x 0 x 0 x x 0 1 x  sin x 12 lOMoAR cPSD| 58833082
TÀI LIỆU TỔNG HỢP BÀI TẬP MÔN GIẢI TÍCH 1 NẰM TRONG ĐỀ THI
CUỐI KỲ CÁC NĂM GẦN ĐÂY VÀ LỜI GIẢI MỘT SỐ BÀI MẪU. +) lim  lim  0 x 0 x 0 x +) f (0)  0
 Hàm số liên tục tại x 0 x sinx f x( ) f x( 0) 0 x
 limx 0 x sin2 x  limx 0 1 cosx  limx 0
f x ( )  limx 0  lim x 0 sinx  0 x 0 x 0 x 2x 2 Vậy f  (0)  0 Bài 3 (K63):  ln(1 2x2 )  ;x  0 Tìm a, b để hàm số  x Khả vi trên R   x2   axb x;  0 Ta có: - Xét liên tục 2 2 ln(1 2x ) 2x +lim f x( )  lim  lim  lim  2x  0 x 0 x 0  x x 0 x x 0 + lim f x( )  lim (x2    ax b) b   x 0 x 0 + f (0)  b
Để hàm số liên tục trên R thì b  0 - Xét tính khả vi: 13 lOMoAR cPSD| 58833082
TÀI LIỆU TỔNG HỢP BÀI TẬP MÔN GIẢI TÍCH 1 NẰM TRONG ĐỀ THI
CUỐI KỲ CÁC NĂM GẦN ĐÂY VÀ LỜI GIẢI MỘT SỐ BÀI MẪU. ln(1 2x2) f x( ) f (0)2x2 + f(0 )   limx 0  limx 0  limx 0 2  2 x  0 x  0 x f x( )  f (0) x2  ax  0 + f    lim   lim   a (0 ) x 0 x 0 x  0 x  0  a  2
Vậy để hàm khả vi thì a   2   b  0
CÁC BÀI TẬP CÒN LẠI SẼ ĐƯỢC CHỮA TRỰC TIẾP TẠI CLB
THAM GIA GROUP: “Góc Học Tập ĐHXD” để nhận tài liệu và thông tin về lớp chữa đề
Bài 4 (K62):Chứng minh rằng:  1  2017x.sin khi x  0 f x( )   2017x
liên tục tại x 0 nhưng không khả vi tại đó.   0 khi x  0  exsin x  1  ; x  0
Bài 5 (K62): Tìm a, b để: f x( )   x Khả vi tại x 0   x2   axb; x  0 Bài 6 (K62)  1 cos neu x x  0 f x( )   x 14 lOMoAR cPSD| 58833082
TÀI LIỆU TỔNG HỢP BÀI TẬP MÔN GIẢI TÍCH 1 NẰM TRONG ĐỀ THI
CUỐI KỲ CÁC NĂM GẦN ĐÂY VÀ LỜI GIẢI MỘT SỐ BÀI MẪU.  1 e +x neu x  0
CMR: Hàm có đạo hàm cấp 1 tại 0 nhưng không có đạo hàm cấp 2 tại 0.
Bài 7 (K61) Tìm a R để f x( )  x  2016.sinax khả vi tại x 2016
Bài 8 (K58)CMR hàm f x( )  x  1.sin x
2) Dạng 2: Khai triển Maclaurin và ứng dụng
- Khai triển Maclaurin của 1 số hàm thường gặp
Bài 1 (K64): Khai triển maclaurin hàm ex 2 đến cấp 5=?
Bài 2 (K63): Viết khai triển Maclaurin của hàm số ex2 =?
Bài 3 (K63): Khai triển hàm Maclaurin hàm f x( )   ? 3 x
Bài 4 (K63) Viết triển khai Maclaurin của hàm số f x( )  2 với phần 1 x Bài 5 (K63)
Viết khai triển Maclaurin của hàm số y  (x2  1)sin2x với phần dư peano tới x11, từ đó y(11)(0)  ? Bài 6 (K63)
Khai triển Maclaurin của hàm số f x( )  (1 x).sin2x đến cấp 10. Từ đó, hãy tính f (10)(0) Bài 7 (K63) x
Viết khai triển Maclaurin hàm số f x( ) 
2 với phần dư dạng peano đến cấp 5, 1  x x từu đó tính f 5(0) 15 lOMoAR cPSD| 58833082
TÀI LIỆU TỔNG HỢP BÀI TẬP MÔN GIẢI TÍCH 1 NẰM TRONG ĐỀ THI
CUỐI KỲ CÁC NĂM GẦN ĐÂY VÀ LỜI GIẢI MỘT SỐ BÀI MẪU.
Bài 8 (K62) Khai triển Maclaurin của hàm f x( ) 
4) Dạng 4: Tính đạo hàm 1
Bài 1 (K64): Tính đạo hàm cấp n của các hàm: f x( )  2 x  4
Bài 2 (K62): Cho hàm y  sin4 x. Tính y10(0)  ?
Bài 3 (K63) Tính đạo hàm cấp n của f x( )  sin2 x
Bài 4 (K62) Tính đạo hàm cấp n của f x( )  x2.sin2x
Bài 5 (K64) Tính đạo hàm cấp n của f x( )  (x2   x 1).ex
Bài 6 (K61) Cho hàm số f x( ) 
 sin3 x. Hãy tính f (8)       2
Bài 7 (K62) Cho hàm số y  cos4 x. Tính y(10)(0)
Bài 8 (K63) Cho hàm số y  x2 sin 22 x . Tính y (9) (0) (Đề K56)
Bài 9 (K64) Cho hàm số y  cos3 x . Hãy tính f (7)  (Đề K58) ( ) 2
Bài 10 (K63) Tính đạo hàm cấp n của y  ln(x2   3x 2)
Bài 11 (K62) Tính đạo hàm cấp n của hàm số
a) f x( )  (x2   x 1).e2x c) f x( )  x2.sin3x 2 x b) f x( )  sin3 .cos2x x d) g( )x  1 x II) Chương 3: Tích Phân 8 16 lOMoAR cPSD| 58833082
TÀI LIỆU TỔNG HỢP BÀI TẬP MÔN GIẢI TÍCH 1 NẰM TRONG ĐỀ THI
CUỐI KỲ CÁC NĂM GẦN ĐÂY VÀ LỜI GIẢI MỘT SỐ BÀI MẪU.
Bài 1 (K62) Tính tích phân bất định sau: I  x 2  2 3x2  dx
Bài 2 (K64) Tính tích phân bất định dx dx  x a) 2 3 b)  2  1  x  2x 3 x dx2
Bài 3 (K64) Tính tích phân bất định I   2 x  1 dx 
Bài 4 (K61) Tính tích phân bất định: I  2 3  1 x 
Bài 5 (K62) Tính I   (x2  x  1)2 dx
Bài 6 (K63) Tính I   tan2 xdx
Bài 7 (K63) Tính tích phân   sin5x  4.44x  cos3x  2 dx:
Bài 8 (K64) Tính tích phân 1
I   0 x 1 3x 1dx 1 17 lOMoAR cPSD| 58833082
TÀI LIỆU TỔNG HỢP BÀI TẬP MÔN GIẢI TÍCH 1 NẰM TRONG ĐỀ THI
CUỐI KỲ CÁC NĂM GẦN ĐÂY VÀ LỜI GIẢI MỘT SỐ BÀI MẪU. Bài 9 (K61) Tính I   dx 3 Bài 10 (K64) Tính I  Bài 11 (K63) Tính I 2 1  Bài 12 (K64) Tính I  Bài 13 (K63) Tính I  1 sin x  cos x
* Sử dụng phương pháp tích phân từng phần.
Bài 14 (K62) Tính I    x2  1 . arctan
xdx Bài 15 (K63) Tính I   cos ln x dx e2 dx Bài 16 (K64) Tính I   e Bài 17 (K62) Tính I   0ln2
* Những câu tích phân trong đề các năm gần đây. 18 lOMoAR cPSD| 58833082
TÀI LIỆU TỔNG HỢP BÀI TẬP MÔN GIẢI TÍCH 1 NẰM TRONG ĐỀ THI
CUỐI KỲ CÁC NĂM GẦN ĐÂY VÀ LỜI GIẢI MỘT SỐ BÀI MẪU. 3 
Bài 18 (K62) Tính tích phân 1 x3  x  3 x.sin x  Bài 19 (K63) Tính I  cos2 x dx  3  x 4  Bài 20 (K64) I =
 x 2  x 1 dx 2x3  x2  5x  1  Bài 21 (K62) Tính I =
 x2  3  x2  x  1  K62  2sin x  3cosx dx Bài 22 (K63) Tính I   sin x  4cosx (sin x  cos x  3)dx  Bài 23 (K64) I  3sin x  4cos x  5
2) Dạng 2: Tích phân suy rộng (loại 1 và loại 2)   1
Bài 1 (K63) xét sự hội tụ của tích phân và xét hội tụ I   1 x2(x  1)dx   xdx
Bài 2 (K64) Tích phân suy rộng  2 x2  1 và xét phân ki 19 lOMoAR cPSD| 58833082
TÀI LIỆU TỔNG HỢP BÀI TẬP MÔN GIẢI TÍCH 1 NẰM TRONG ĐỀ THI
CUỐI KỲ CÁC NĂM GẦN ĐÂY VÀ LỜI GIẢI MỘT SỐ BÀI MẪU. Bài 3 (K65)   xdx Tính I   2
x3  1 Tích phân suy rộng.
Bài 4. Tích phân suy rộng (K63) a dx I   3 x2   x 6dx   dx
Bài 5. Tích phân suy rộng (k64) I   2  x  1  x  1   dx Bài 6 (K62) Tính I 
 1  x  1  x  1 ( Tích phân suy rộng)  
Bài 7 (K62) Tích phân suy rộng. Tính I   0 xe.  2015xdx Xét sự hội tụ   sin x
Bài 8 (K63) Xét sự hội tụ của tích phân suy rộng  o x2  1dx   xdx
Bài 9 (K63) Xét sự hội tụ và pk của tích phân suy rộng  1 2 2 1 x  1 x  1
Bài 10 (K63) Tính tích phân suy rộng  0
Bài 11 (K64) Tính tích phân suy rộng  3 2x2   5x 2   Cos x
Bài 12 (K63) Xét sự hội tụ của tích phân suy rộng  0 x2  4dx 20