Giải Toán 10 Bài 3: Tích của một số với một vectơ | Chân trời sáng tạo
Giải Toán 10 Chân trời sáng tạo bài 3 được biên soạn với các lời giải chi tiết, đầy đủ và chính xác bám sát chương trình sách giáo khoa môn Toán 10 tập 1. Giải Toán 10 bài 3 Chân trời sáng tạo là tài liệu cực kì hữu ích hỗ trợ các em học sinh
Chủ đề: Chương 5: Vecto (CTST)
Môn: Toán 10
Sách: Chân trời sáng tạo
Thông tin:
Tác giả:
Preview text:
Toán 10 Bài 3: Tích của một số với một vectơ
Trả lời câu hỏi Thực hành Toán 10 Bài 3 Thực hành 1 Cho hai vecto
và một điểm M như Hình 3. a) Hãy vẽ các vecto
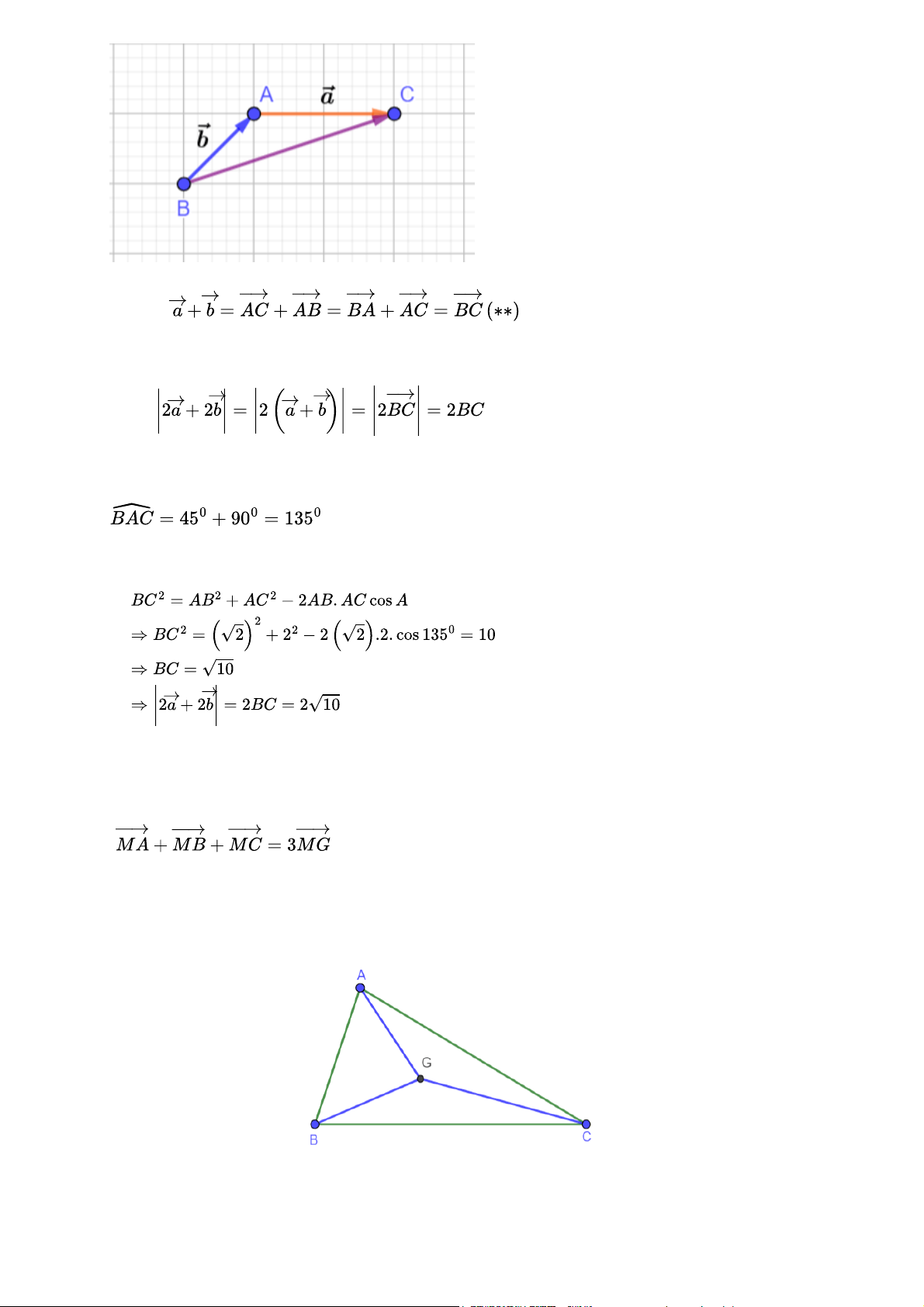
b) Cho biết mỗi ô vương có cạnh bằng 1. Tính Gợi ý đáp án a) Ta có:
Từ M vẽ đường thẳng song song với giá của
, lấy điểm N trên đường thẳng đó cùng hướng với vecto thỏa mãn Ta lại có:
Từ M vẽ đường thẳng song song với giá của
, lấy điểm P trên đường thẳng đó ngược hướng với vecto thỏa mãn
b) Đường chéo mỗi ô vuông có độ dài là Ta có: Khi đó: Ta có: (*) Đặt kí hiệu như hình vẽ: Ta có: Từ (*) và (**) => Xét tam giác ABC ta có:
Áp dụng định lí cosin trong tam giác ta có: Thực hành 2
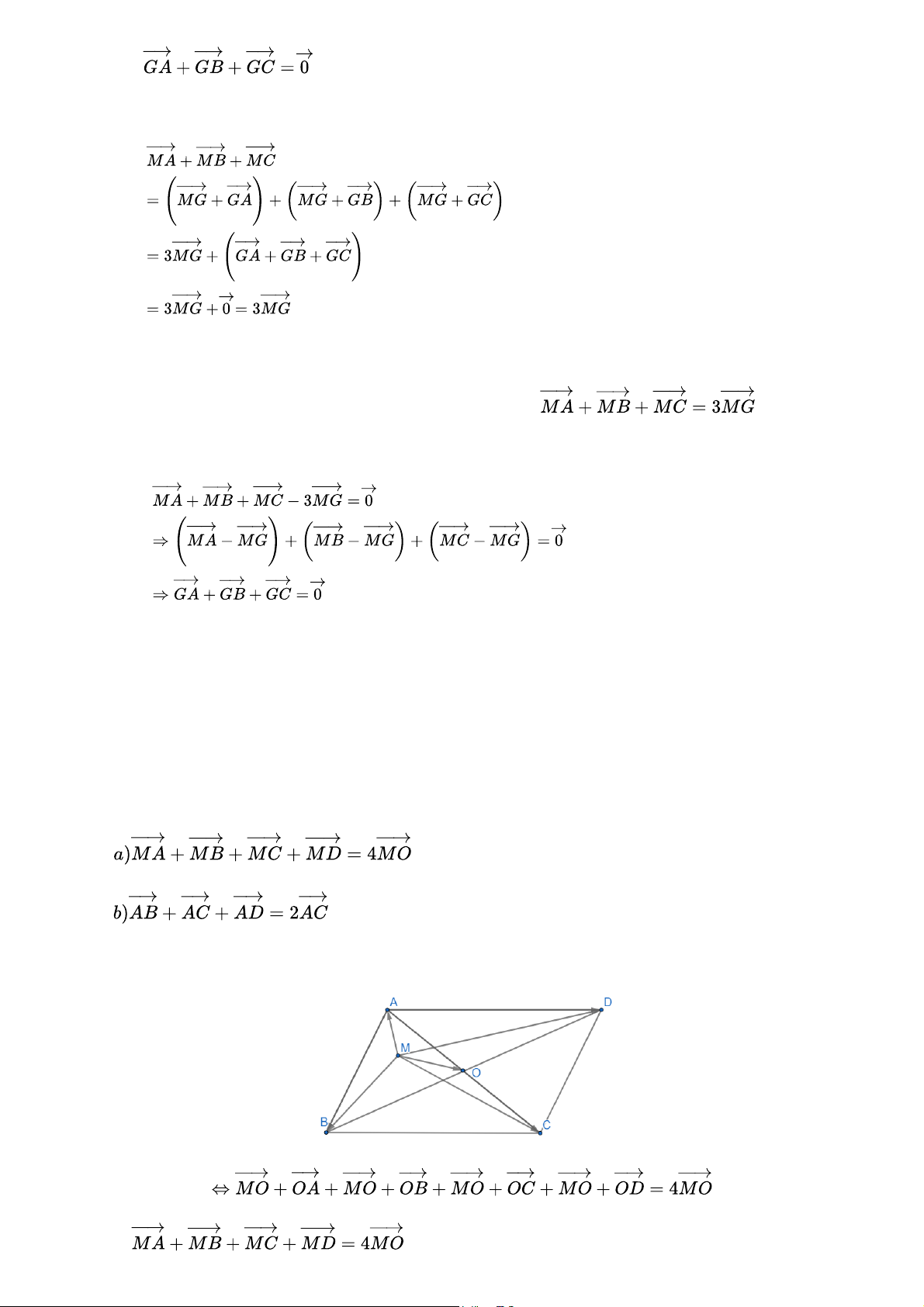
Cho tam giác ABC. Chứng minh G là trọng tâm của tam giác ABC khi và chỉ khi Gợi ý đáp án Hình vẽ minh họa:
Giả sử G là trọng tâm tam giác ABC => Khi đó:
Chứng minh chiều ngược lại
Giả sử tam giác ABC có hai điểm M và G bất kì thỏa mãn Khi đó:
Vậy G là trọng tâm tam giác ABC
Giải Toán 10 trang 97 Chân trời sáng tạo - Tập 1 Bài 1 trang 97
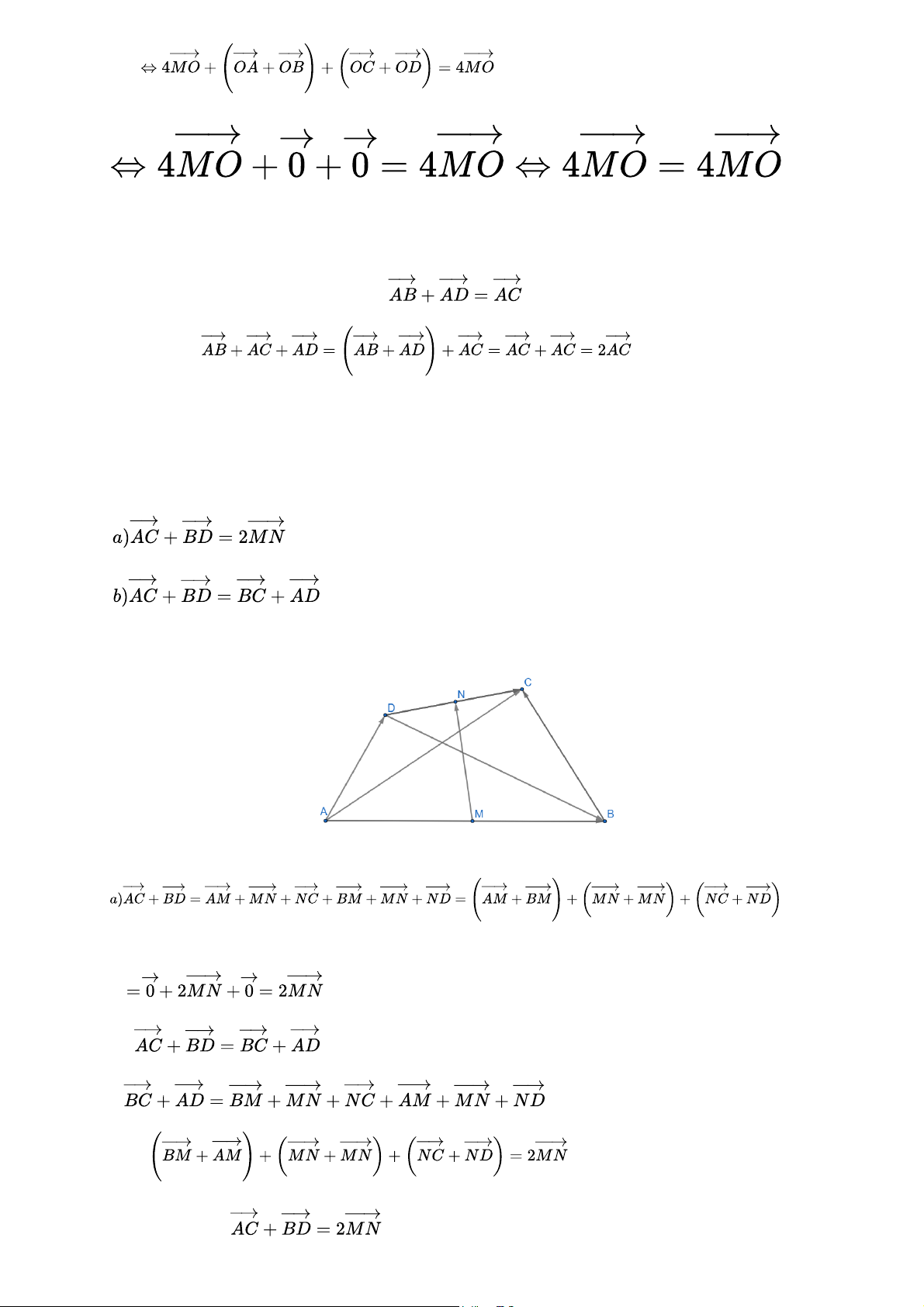
Cho hình bình hành ABCD D có O là giao điểm hai đường chéo. Với M là điểm tùy ý, chứng minh rằng: Gợi ý đáp án a) (luôn đúng)
(vì O là giao điểm 2 đường chéo nên là trung điểm của AB, CD)
b) ABCD là hình bình hành nên ta có Suy ra (đpcm) Bài 2 trang 97
Cho tứ giác ABCD gọi M và N lần lượt là trung điểm của các cạnh AB và CD . Chứng minh rằng Gợi ý đáp án (đpcm) b) Mặt khác ta có: Suy ra Bài 3 trang 97
Cho hai điểm phân biệt A và B. Xác định điểm M sao cho Gợi ý đáp án à ơ ngược hướng
Suy ra M nằm giữa AB sao cho Bài 4 trang 97
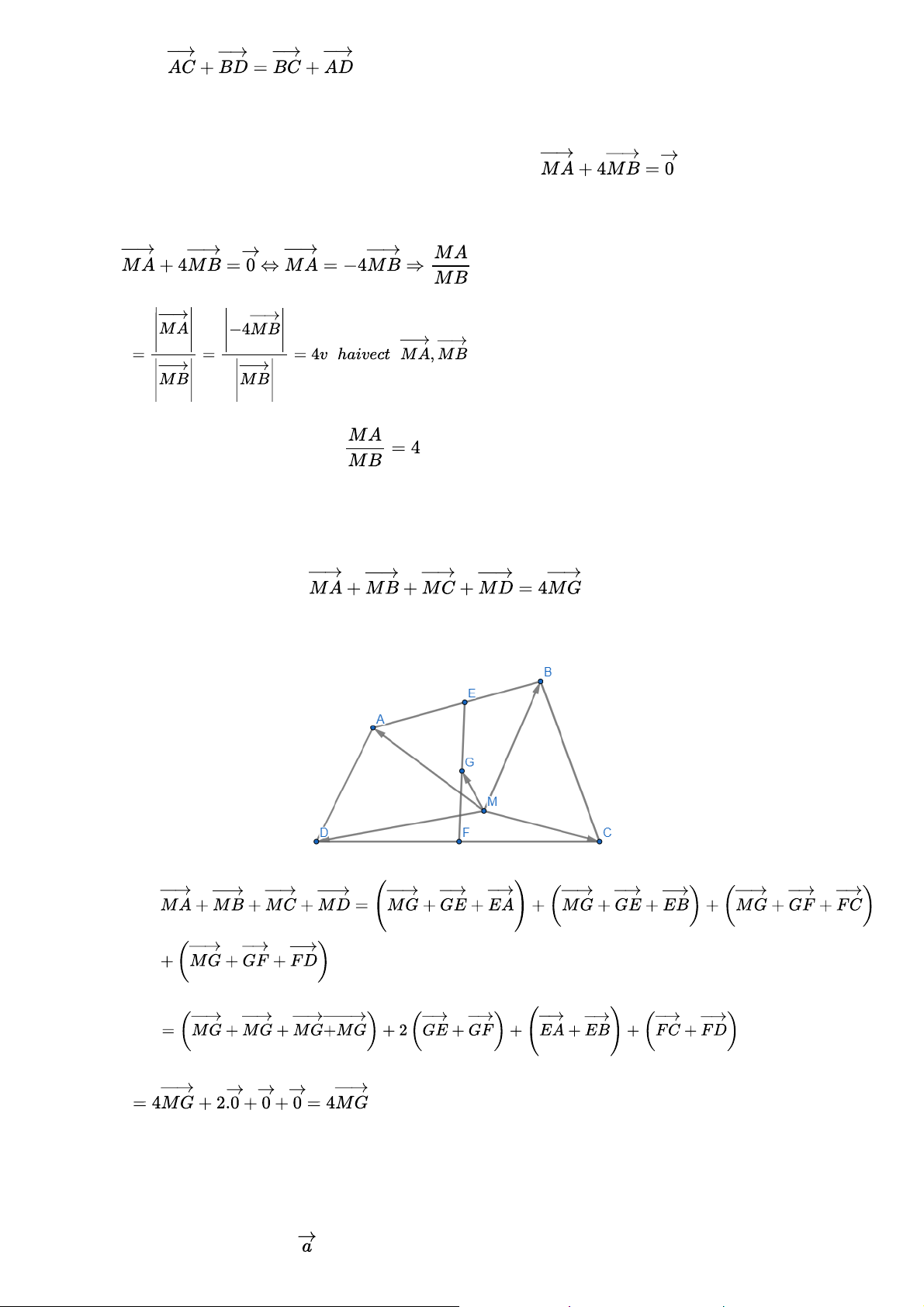
Cho tứ giác ABCD. Gọi E, F, G lần lượt là trung điểm của các đoạn thẳng AB, CD, EF. Lấy điểm
M tùy ý, chứng minh rằng Gợi ý đáp án (đpcm) Bài 5 trang 97
Máy bay A đang bay về hướng Đông Bắc với tốc độ 600 km/h. Cùng lúc đó, máy bay B đang
bay về hướng Tây Nam với tốc độ 800 km/h. Biểu diễn vectơ vận tốc \overrightarrow b của máy
bay B theo vectơ vận tốc của máy bay A Gợi ý đáp án vectơ
là vectơ vận tốc của máy bay A và máy bay b. Do đó
lần lượt là độ lớn của vectơ vận tốc tương ứng. Ta có:
Hai hướng Đông Bắc và Tây Nam là ngược nhau, do đó Bài 6 trang 97
Cho 2 điểm phân biệt A và B
a) Xác định điểm O sao cho
b) Chứng minh rằng với mọi điểm M, ta có Gợi ý đáp án
Vậy O thuộc đoạn AB sao cho b) Ta có: đ Bài 7 trang 97 Cho tam giác ABC
a) Xác định các điểm M, N, P thỏa mãn: b) Biểu thị mỗi vectơ theo hai vectơ
c) Chứng minh ba điểm M, N, P thẳng hàng Gợi ý đáp án a) Ta có: +) và
cùng hướng; tỉ số độ dài
nằm ngoài đoạn thẳng BC sao cho
thuộc đoạn thẳng AB và
là trung điểm của CA c) Ta có: Vậy M,N,P thẳng hàng
Lý thuyết Tích của một số với một vectơ
+) Tích của một vectơ
với một số thực k là một vectơ, kí kiệu là . +) vectơ có độ dài bằng và Cùng hướng với vectơ nếu k > 0
Ngược hướng với vectơ nếu k < 0 +) Quy ước: Nhận xét: Hai vectơ và
cùng phương khi và chỉ khi tồn tại k để