Giải Toán 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác | Kết nối tri thức
Giải Toán 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác | Kết nối tri thức được trình bày khoa học, chi tiết giúp cho các bạn học sinh chuẩn bị bài một cách nhanh chóng và đầy đủ đồng thời giúp quý thầy cô tham khảo để soạn giáo án cho học sinh của mình. Thầy cô và các bạn xem, tải về ở bên dưới.
Chủ đề: Chương 4: Tam giác bằng nhau (KNTT)
Môn: Toán 7
Sách: Kết nối tri thức
Thông tin:
Tác giả:
Tài liệu liên quan:
Preview text:
Giải Toán 7 bài 14: Trường hợp bằng nhau thứ hai và thứ
ba của tam giác sách Kết nối tri thức với cuộc sống
Giải Toán 7 Kết nối tri thức với cuộc sống tập 1 bài 14 - Luyện tập Luyện tập 1
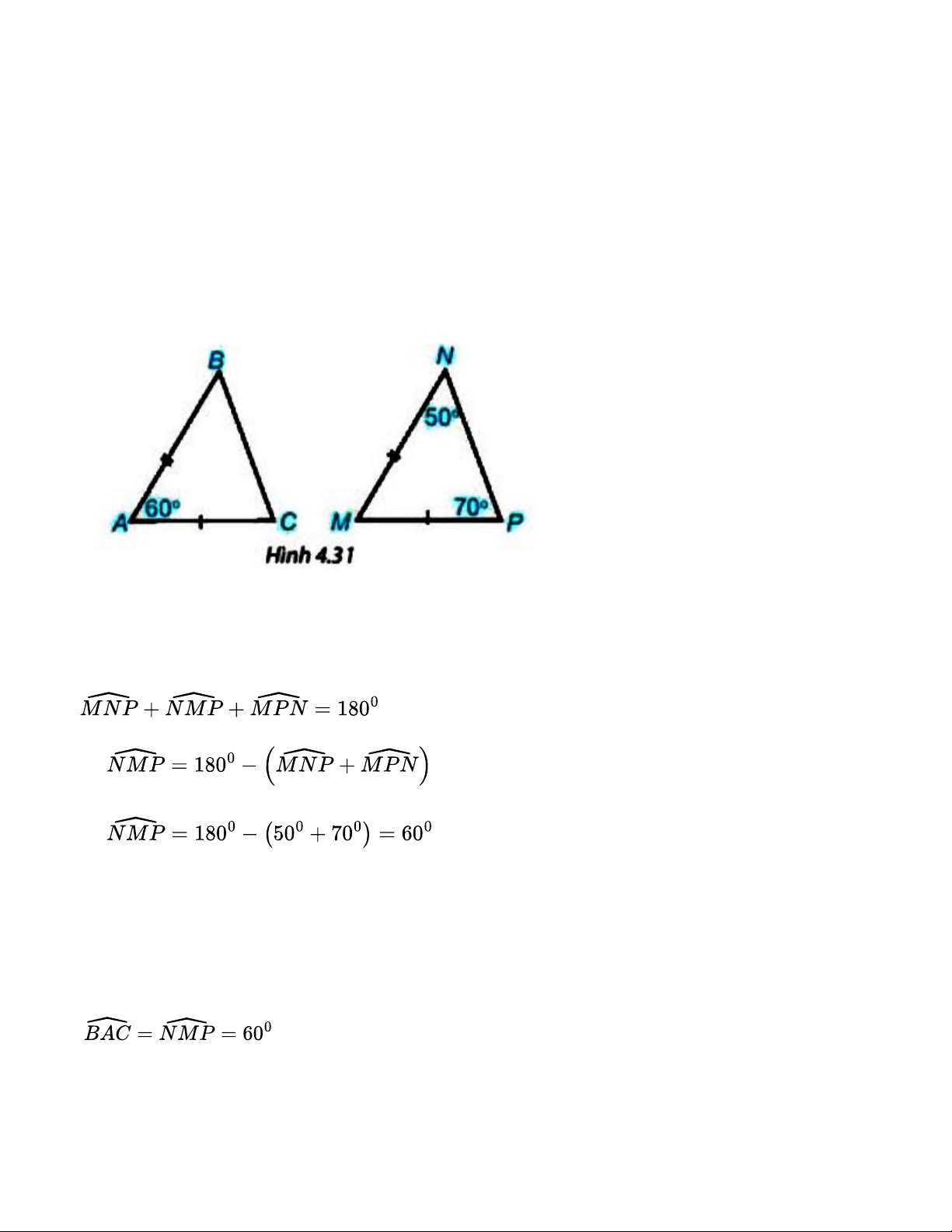
Hai tam giác ABC và MNP trong hình 4.31 có bằng nhau không? Vì sao? Gợi ý đáp án: Xét tam giác MNP có: => =>
Xét tam giác MNP và tam giác ABC ta có: AB = MN (giả thiết) AC = MP (giả thiết)
=> ∆ABC = ∆MNP (c – g – c) Luyện tập 2
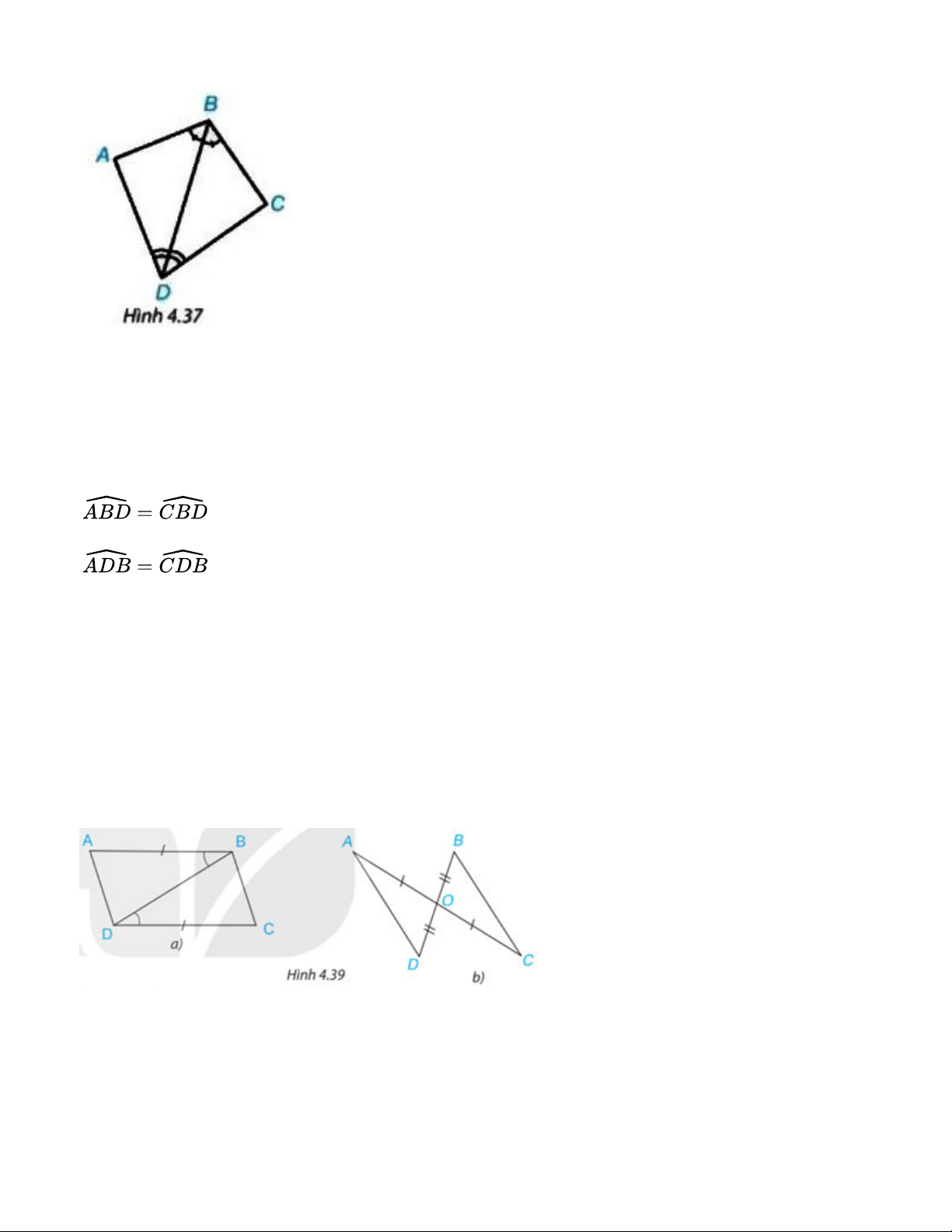
Chứng minh hai tam giác ABD và CBD trong Hình 4.37 bằng nhau. Gợi ý đáp án:
Xét tam giác ABD và tam giác CBD ta có: Cạnh BD chung (giả thiết) (giả thiết)
=> ∆ABD = ∆CBD (g – c - g)
Giải Toán 7 Kết nối tri thức với cuộc sống trang 73 tập 1 Bài 4.12
Trong mỗi hình bên (H.4.39), hãy chỉ ra một cặp tam giác bằng nhau và giải thích vì sao chúng bằng nhau. Gợi ý đáp án:
a) Xét tam giác ABD và tam giác CBD có: AB=CD BD chung Vậy
b) Xét hai tam giác OAD và OCB có: AO=CO (đối đỉnh) OD=OB Vậy Bài 4.13
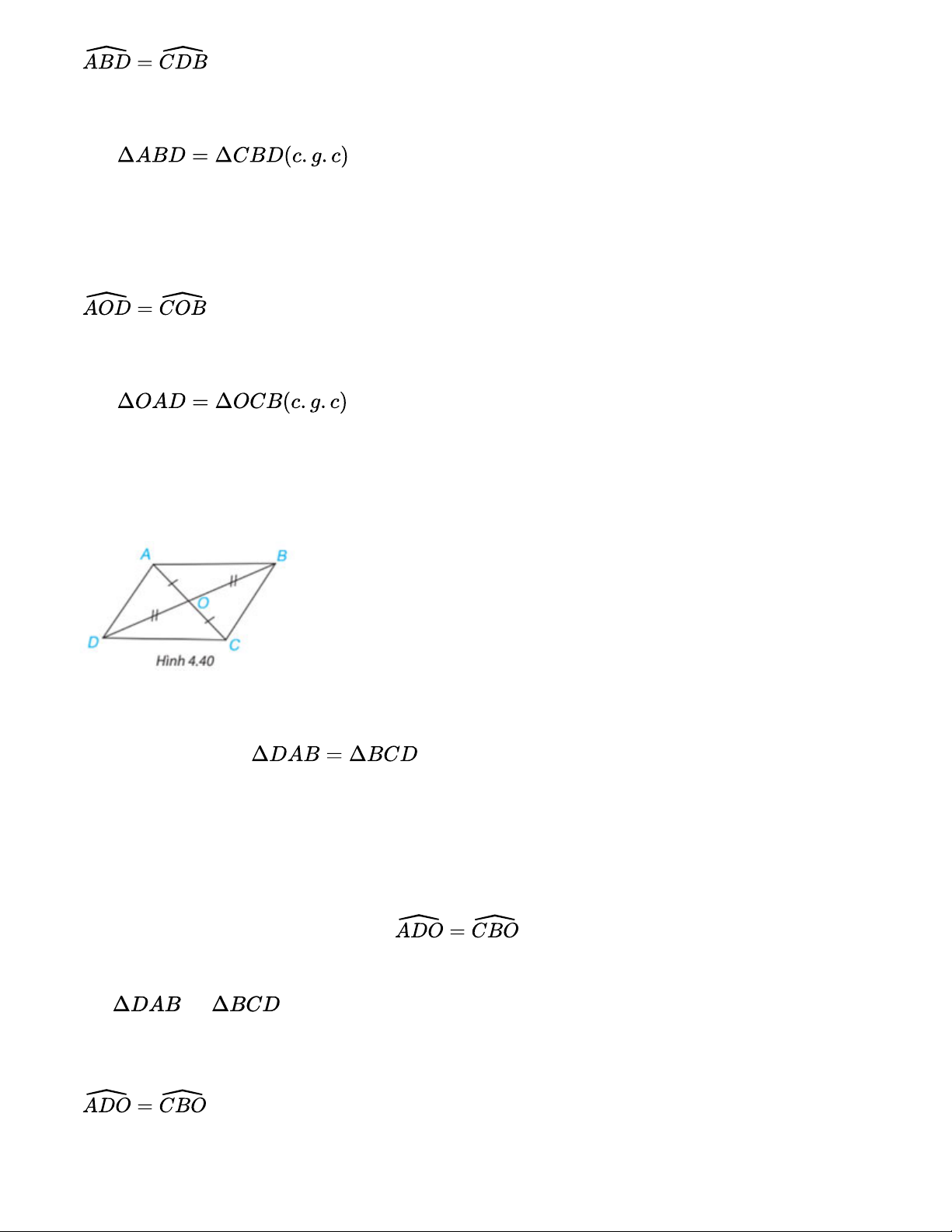
Cho hai đoạn thẳng AC và BD cắt nhau tại điểm O sao cho OA = OC, OB = OD như Hình 4.40.
a) Hãy tìm hai cặp tam giác có chung đỉnh O bằng nhau; b) Chứng minh rằng . Gợi ý đáp án:
a) Hai cặp tam giác có chung đỉnh O bằng nhau là: AOB và COD; AOD và COB theo trường
hợp cạnh – góc – cạnh.
b) Do hai tam giác AOD và COB nên:
(2 góc tương ứng) và AD=BC (2 cạnh tương ứng) Xét và có: AD=BC BD chung Vậy Bài 4.14
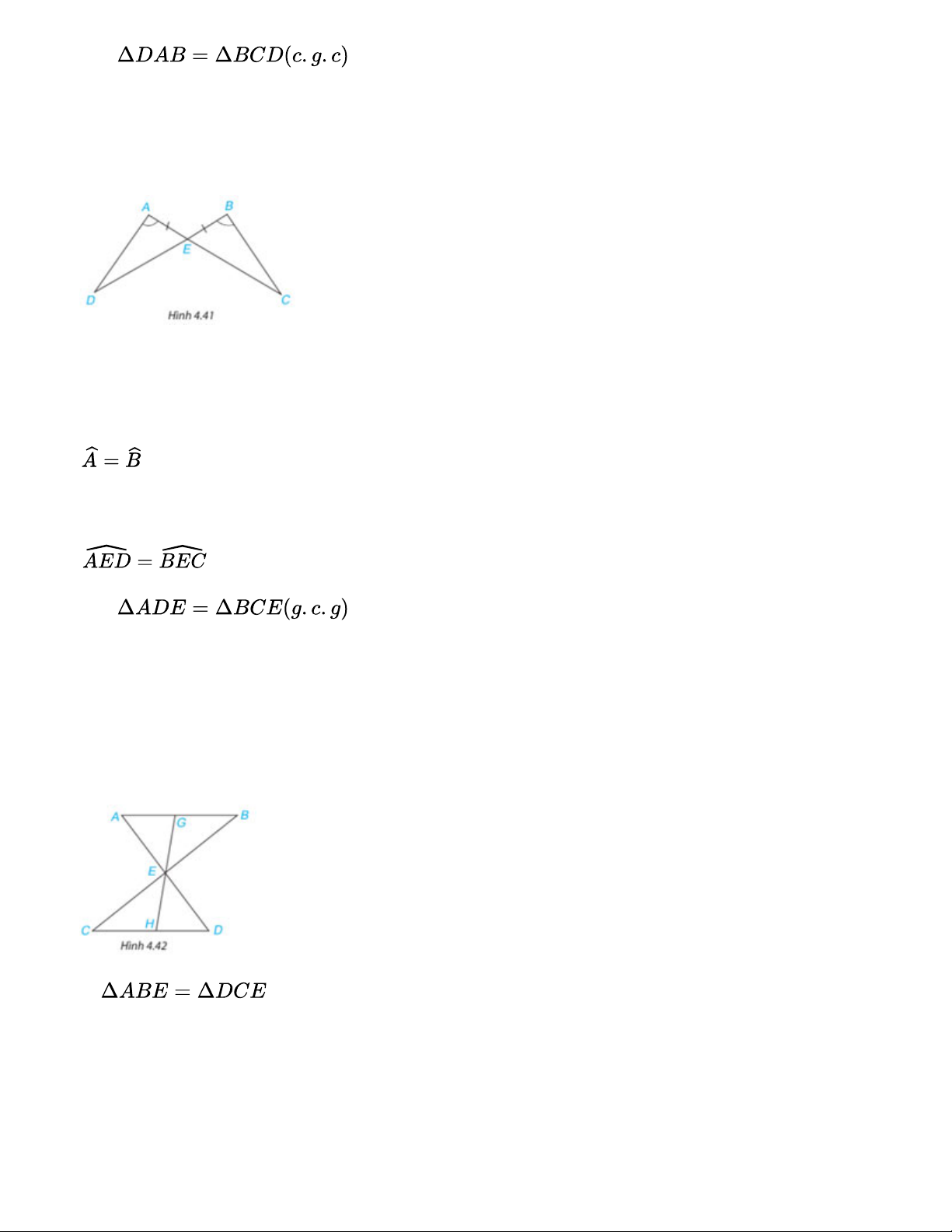
Chứng minh rằng hai tam giác ADE và BCE trong Hình 4.41 bằng nhau. Gợi ý đáp án:
Xét hai tam giác ADE và BCE có: AE=BE (đối đỉnh) Vậy Bài 4.15
Cho đoạn thẳng AB song song và bằng đoạn thẳng CD như Hình 4.42. Gọi E là giao điểm của
hai đường thẳng AD và BC. Hai điểm G và H lần lượt nằm trên AB và CD sao cho G, E, H
thẳng hàng. Chứng minh rằng: a) ; b) EG = EH. Gợi ý đáp án:
a)Xét hai tam giác ABE và DCE có: (so le trong) AB=CD(gt) (so le trong) Vậy
b)Xét hai tam giác BEG và CEH có: (đối đỉnh) CE=BE (do ) (so le trong) Suy ra
Vậy EG=EH (hai cạnh tương ứng).