Giải Toán 8 Bài 3: Đường trung bình của tam giác | Cánh diều
Giải Toán 8 Bài 3: Đường trung bình của tam giác | Cánh diều là tài liệu vô cùng hữu ích giúp các em học sinh lớp 8 có thêm nhiều gợi ý tham khảo để giải các bài tập trong SGK Toán 8 Cánh diều. Tài liệu được trình bày rõ ràng, cẩn thận, dễ hiểu nhằm giúp học sinh nhanh chóng biết cách làm bài. Vậy mời các bạn theo dõi bài viết dưới đây!
Chủ đề: Chương 8: Tam giác đồng dạng. Hình đồng dạng (CD)
Môn: Toán 8
Sách: Cánh diều
Thông tin:
Tác giả:
Thông tin :
Chủ đề:
Chương 8: Tam giác đồng dạng. Hình đồng dạng (CD)
Môn:
Sách:
Tác giả:
Tài liệu liên quan:
Preview text:
Toán 8 Bài 3: Đường trung bình của tam giác Cánh diều
Giải Toán 8 Cánh diều Tập 2 trang 65 Bài 1
Cho tam giác ABC có M là trung điểm của AB, điểm N thuộc cạnh AC thỏa mãn MN // BC.
Chứng minh NA = NC và MN = BC. Lời giải:
- Vì MN // BC nên theo định lí Thalès ta có:
Mà AM = MB (M là trung điểm của AB) Suy ra: AN = NC. - Vì MN // BC nên ta có:
Mà AM = AB (M là trung điểm của AB) Do đó: MN = BC. Bài 2
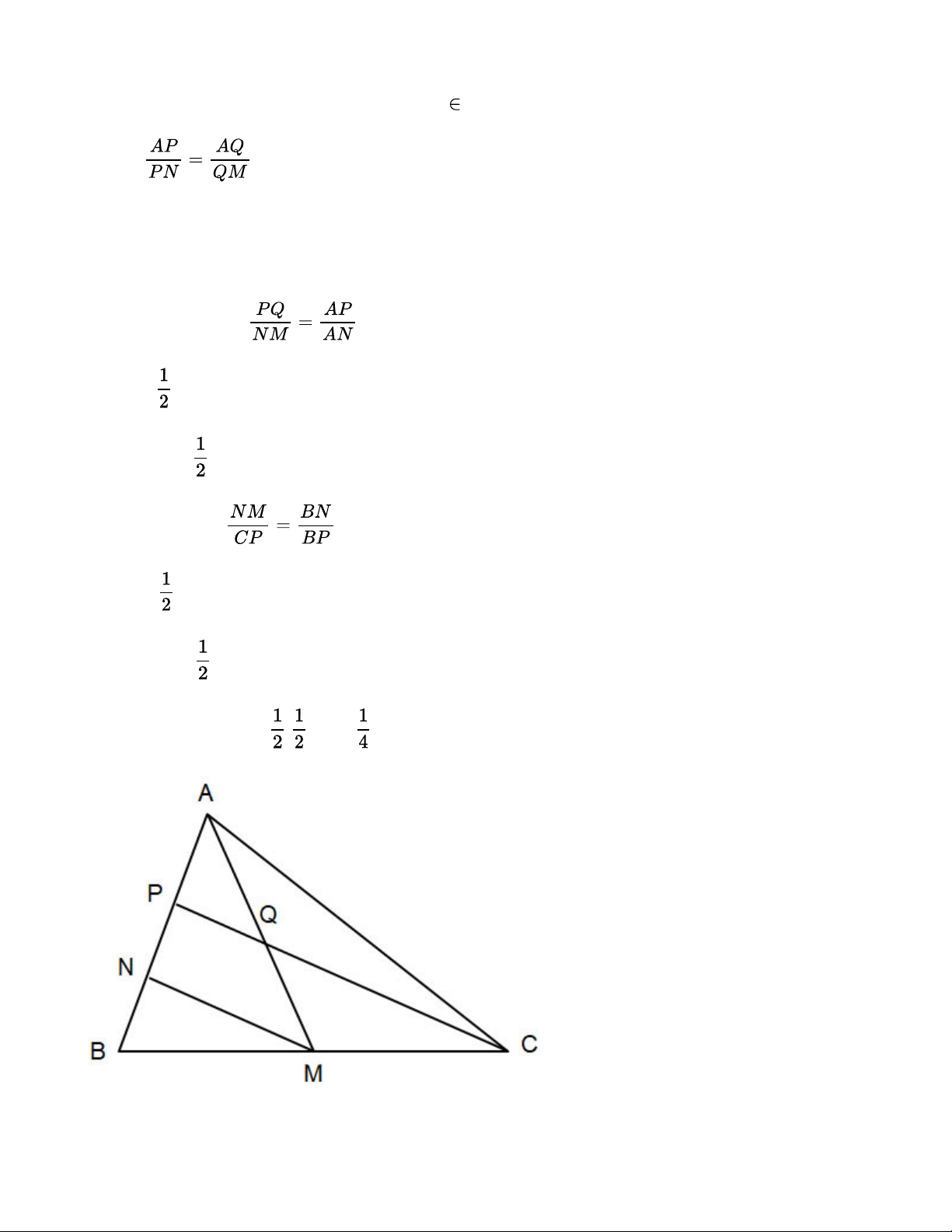
Cho tam giác ABC có AM là đường trung tuyến, các điểm N, P phân biệt thuộc cạnh AB sao cho
AP = PN = NB. Gọi Q là giao điểm của AM và CP. Chứng minh: a) MN // CP; b) AQ = QM; c) CP = 4PQ. Lời giải:
a) Tam giác BCP có: PN = NB; BM = MC (M là trung điểm của BC) Suy ra:
Do đó: MN // CP (Định lí Thalès).
b) Tam giác AMN có: MN // PQ (MN // CP, Q CP) Suy ra: Mà AP = PN Do đó: AQ = QM. c) Do MN // PQ nên Mà AP = AN Suy ra: PQ = NM. (1) Do MN // CP nên Mà BN = BP Suy ra: NM = CP. (2)
Từ (1)(2) suy ra: PQ = . CP = CP hay CP = 4PQ. Bài 3
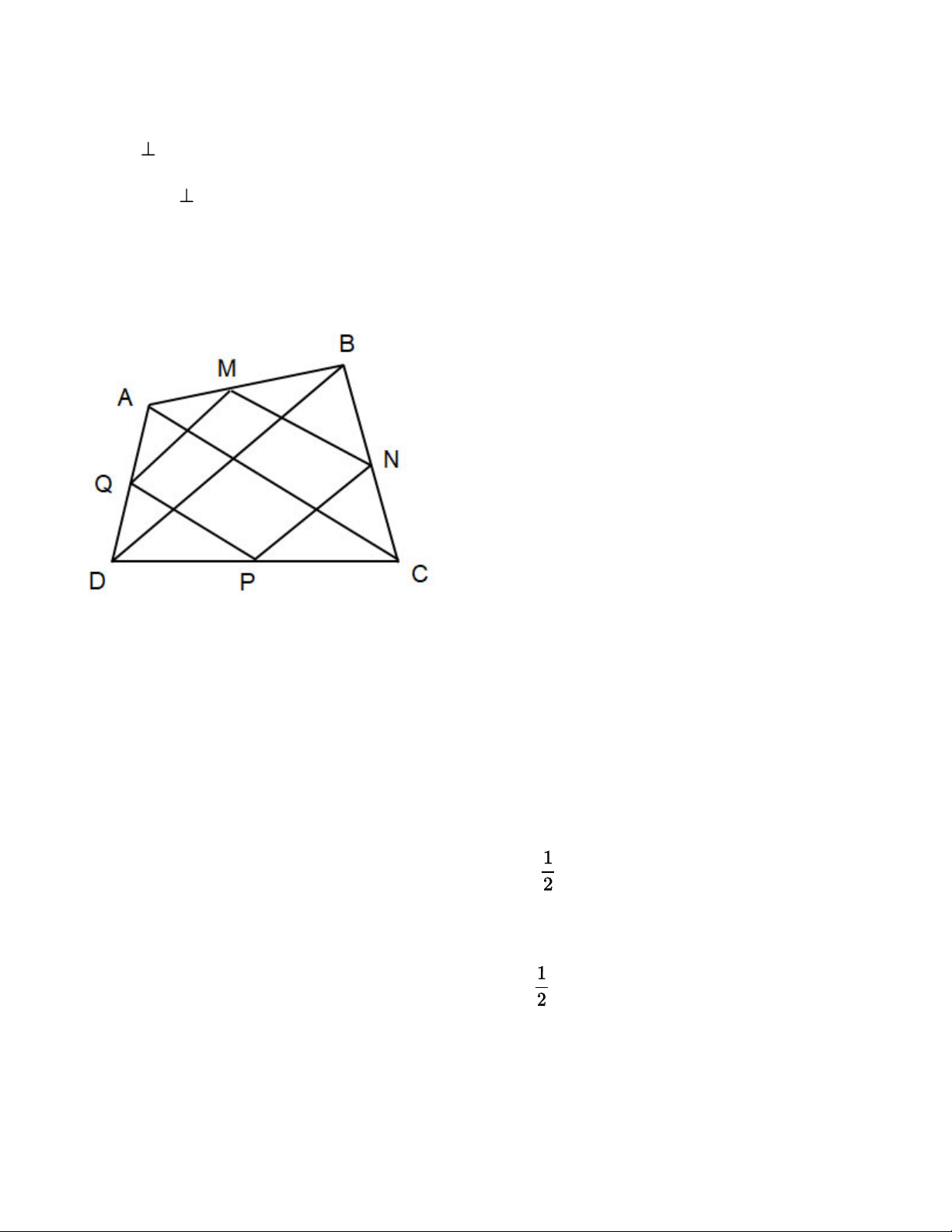
Cho tứ giác ABCD có M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA.
a) Chứng minh tứ giác MNPQ là hình bình hành.
b) Cho AC = BD. Chứng minh tứ giác MNPQ là hình thoi.
c) Cho AC BD. Chứng minh tứ giác MNPQ là hình chữ nhật. Lời giải:
a) Tam giác ABD có: M, Q lần lượt là trung điểm của AB, DA.
Suy ra: MQ là đường trung bình nên MQ // BD (1)
Tam giác BDC có: N, P lần lượt là trung điểm của BC, CD.
Suy ra: NP là đường trung bình nên NP // BD (2)
Từ (1)(2) suy ra: MQ // NP (3)
Tam giác ABC có: M, N lần lượt là trung điểm của AB, BC.
Suy ra: MN là đường trung bình nên MN // AC (4)
Tam giác ADC có: P, Q lần lượt là trung điểm của CD, DA.
Suy ra: PQ là đường trung bình nên PQ // AC (5)
Từ (4)(5) suy ra: MN // PQ (6)
Từ (3)(6) suy ra: MNPQ là hình bình hành.
b) MQ là đường trung bình của tam giác ABD, suy ra MQ = BD
NP là đường trung bình của tam giác BDC, suy ra NP = BD
MN là đường trung bình của tam giác ABC, suy ra MN = AC
PQ là đường trung bình của tam giác ADC, suy ra PQ = AC Mà AC = BD Do đó: MQ = NP = MN = PQ
Mà MNPQ là hình bình hành (cmt) Suy ra: MNPQ là hình thoi. c) Ta có: MQ // BD; MN // AC Mà AC BD Suy ra: MQ MN
Mà MNPQ là hình bình hành (chứng minh câu a)
Do đó: MNPQ là hình chữ nhật. Bài 4
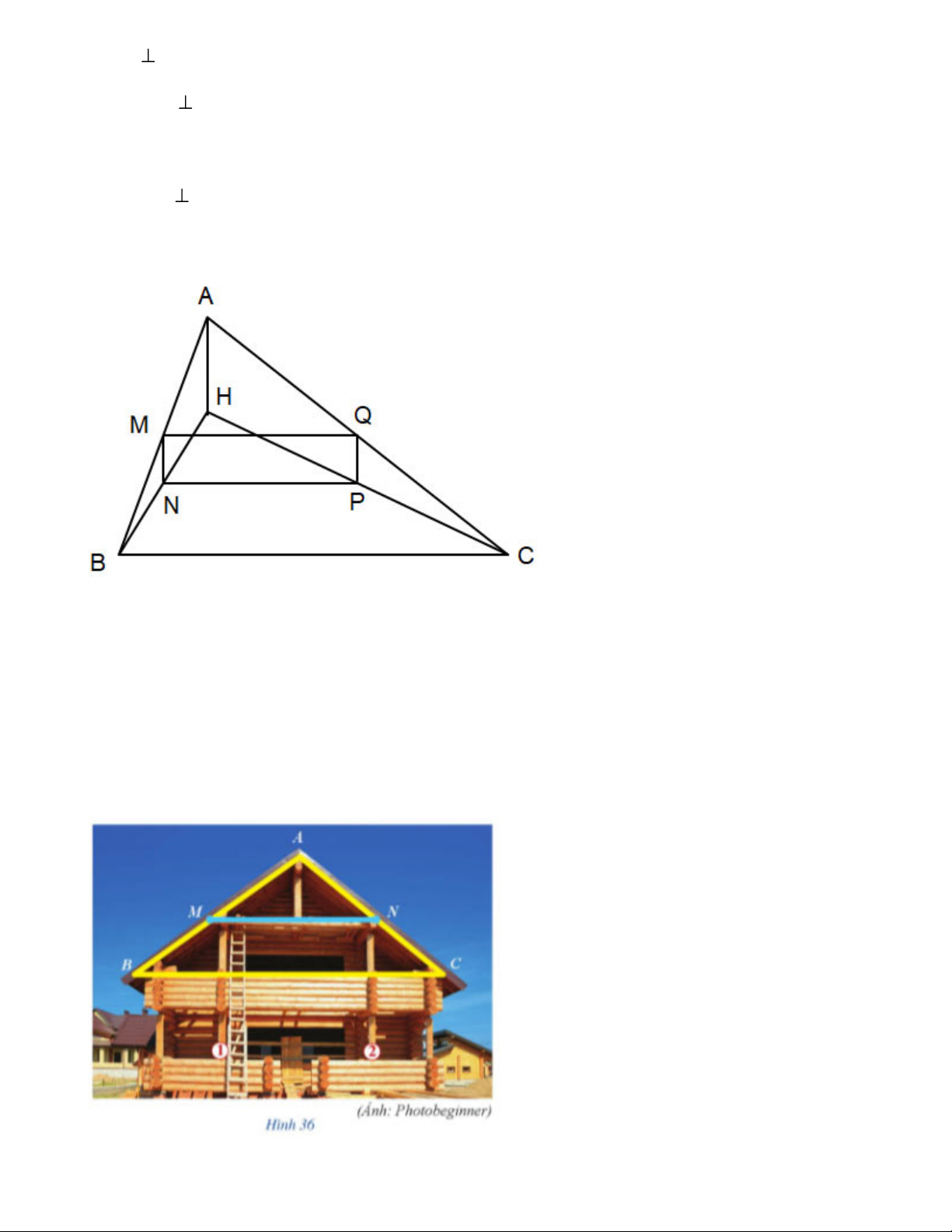
Cho tam giác ABC nhọn có H là trực tâm. Gọi M, N, P, Q lần lượt là trung điểm của các đoạn
thẳng AB, BH, HC, CA. Chứng minh tứ giác MNPQ là hình chữ nhật. Lời giải:
Tam giác ABH có: M, N lần lượt là trung điểm của AB, BH.
Suy ra: MN là đường trung bình nên MN // AH và MN = AH (1)
Tam giác ACH có: P, Q lần lượt là trung điểm của CH, AC.
Suy ra: PQ là đường trung bình nên PQ // AH và PQ = AH (2)
Từ (1)(2) suy ra: MN // PQ và MN = PQ.
Do đó: MNPQ là hình bình hành (3) Ta có: MN // AH
Mà AH BC (H là trực tâm tam giác ABC) Suy ra: MN BC
Mà MQ // BC (MQ là đường trung bình của tam giác ABC) Do đó: MN MQ (4)
Từ (3)(4) suy ra: MNPQ là hình chữ nhật. Bài 5
Trong Hình 36, ba cạnh màu vàng AB, BC, CA gợi nên hình ảnh tam giác ABC và đoạn thẳng
màu xanh MN là một đường trung bình của tam giác đó. Bạn Duyên đứng ở phía dưới đo
khoảng cách giữa hai chân cột số 1 và số 2, từ đó ước lượng được độ dài đoạn thẳng MN
khoảng 4,5 m. Khoảng cách giữa hai mép dưới của mái được tính bằng độ dài đoạn thẳng BC.
Hỏi khoảng cách đó khoảng bao nhiêu mét? Lời giải:
Ta có: MN là đường trung bình của tam giác ABC nên MN = BC hay BC = 2MN
Mà khoảng cách giữa hai mép dưới của mái được tính bằng độ dài đoạn thẳng BC
Suy ra: Khoảng cách đó bằng 2MN hay bằng 2.4,5 = 9 m.