Giải Toán 8 Bài 4: Tính chất đường phân giác của tam giác | Cánh diều
Giải Toán 8 Bài 4: Tính chất đường phân giác của tam giác | Cánh diều là tài liệu vô cùng hữu ích giúp các em học sinh lớp 8 có thêm nhiều gợi ý tham khảo để giải các bài tập trong SGK Toán 8 Cánh diều. Tài liệu được trình bày rõ ràng, cẩn thận, dễ hiểu nhằm giúp học sinh nhanh chóng biết cách làm bài. Vậy mời các bạn theo dõi bài viết dưới đây!
Chủ đề: Chương 8: Tam giác đồng dạng. Hình đồng dạng (CD) 11 tài liệu
Môn: Toán 8 1.9 K tài liệu
Sách: Cánh diều
Tác giả:
Preview text:
Toán 8 Bài 4: Tính chất đường phân giác của tam giác Cánh diều
Giải Toán 8 Cánh diều Tập 2 trang 69 Bài 1
Cho tam giác ABC có ba đường phân giác AD, BE, CF. Biết AB = 4, BC = 5, CA = 6. Tính BD, CE, AF. Lời giải:
AD là đường phân giác của góc BAC nên Mà CD = BC - BD Suy ra: hay Do đó: BD = 2.
BE là đường phân giác của góc ABC nên Mà AE = AC - CE Suy ra: hay Do đó: CE = .
CF là đường phân giác của góc ACB nên Mà BF = AB - AF Suy ra: hay Do đó: AF = . Bài 2
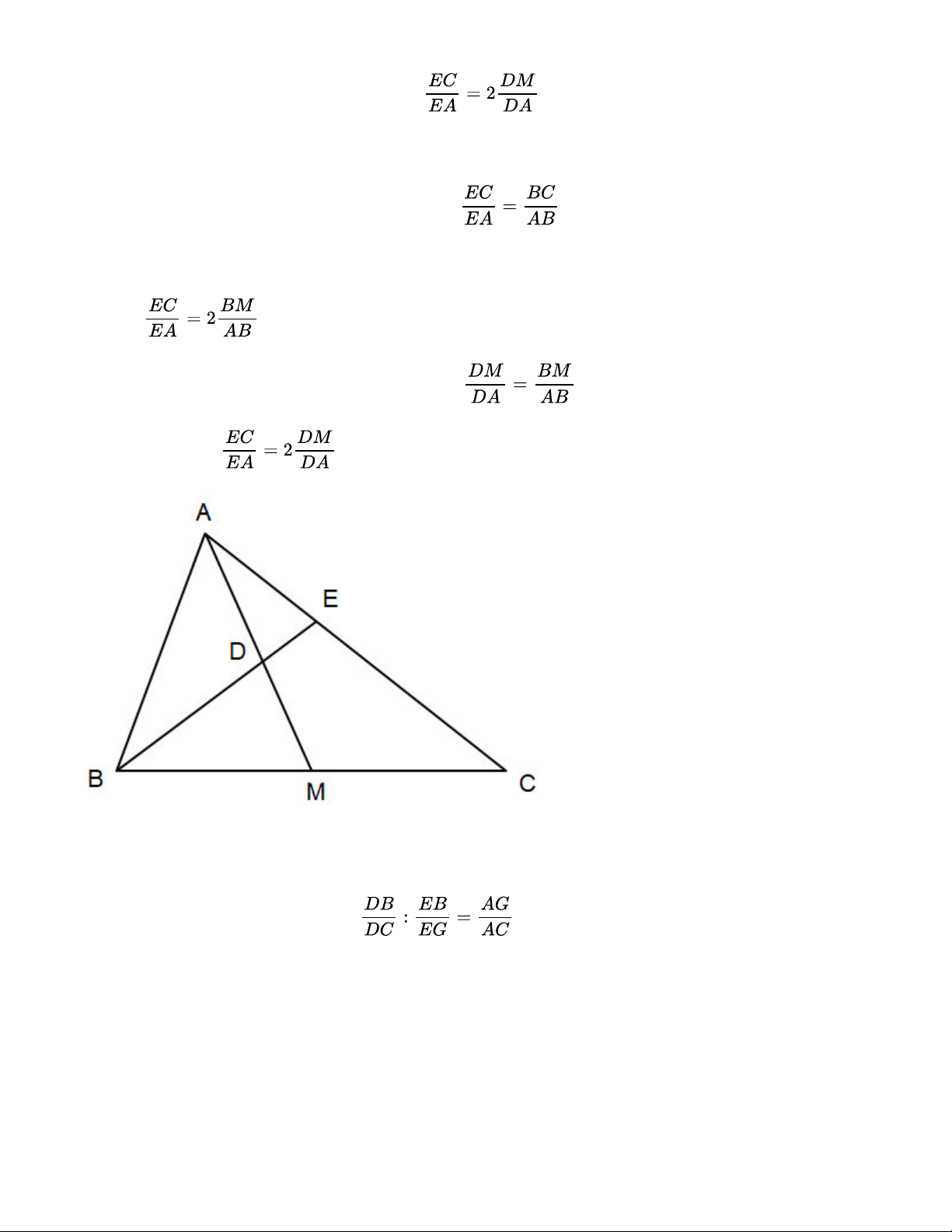
Cho tam giác ABC có đường trung tuyến AM. Tia phân giác của góc ABC lần lượt cắt các đoạn
thẳng AM, AC tại điểm D, E. Chứng minh . Lời giải:
Tam giác ABC có BE là đường phân giác nên
Mà M là trung điểm của BC (AM là đường trung tuyến) nên BC = 2BM Suy ra: (1)
Tam giác ABM có BD là đường phân giác nên (2) Từ (1)(2) suy ra: . Bài 3
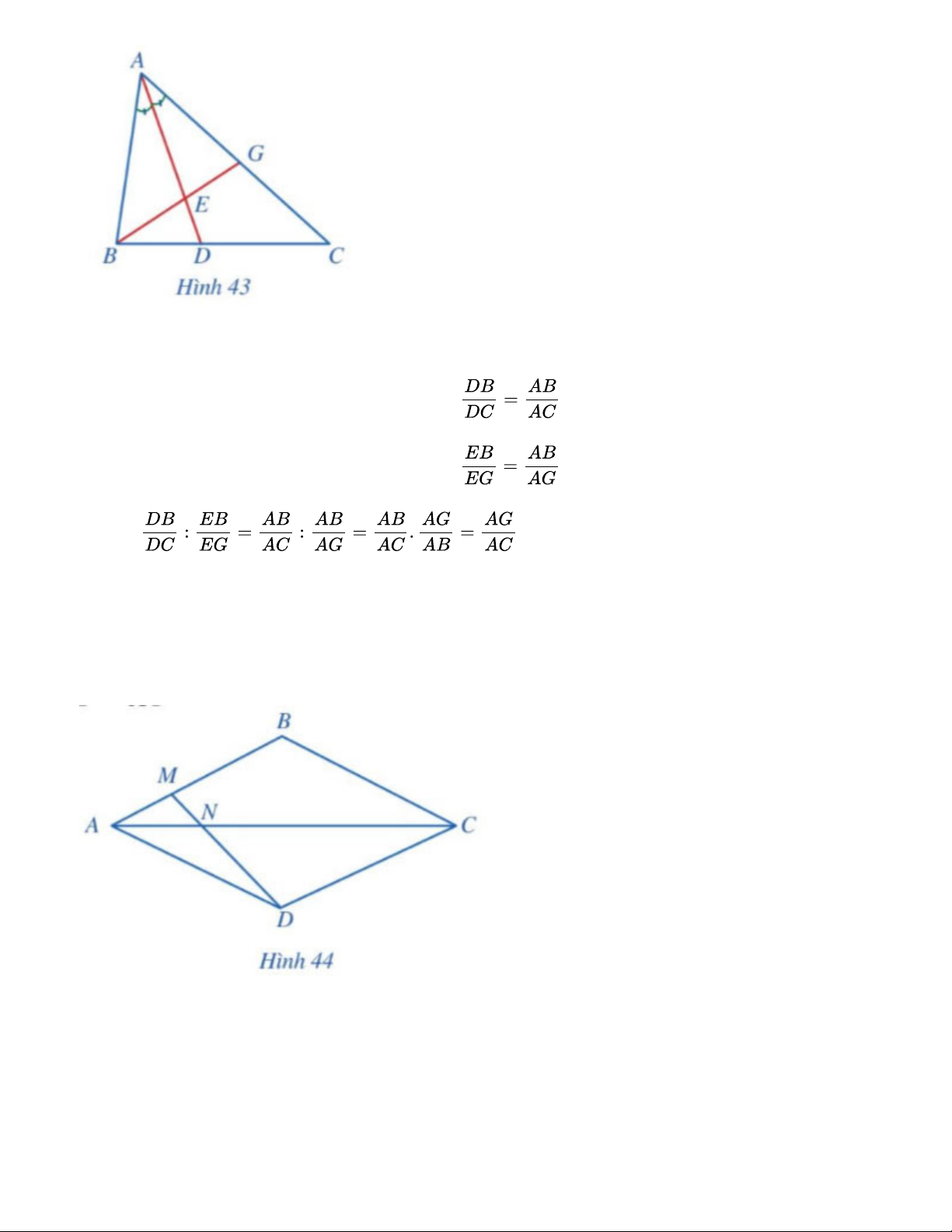
Quan sát Hình 43 và chứng minh . Lời giải:
Tam giác ABC có AD là đường phân giác nên
Tam giác ABG có AE là đường phân giác nên Do đó: . Bài 4
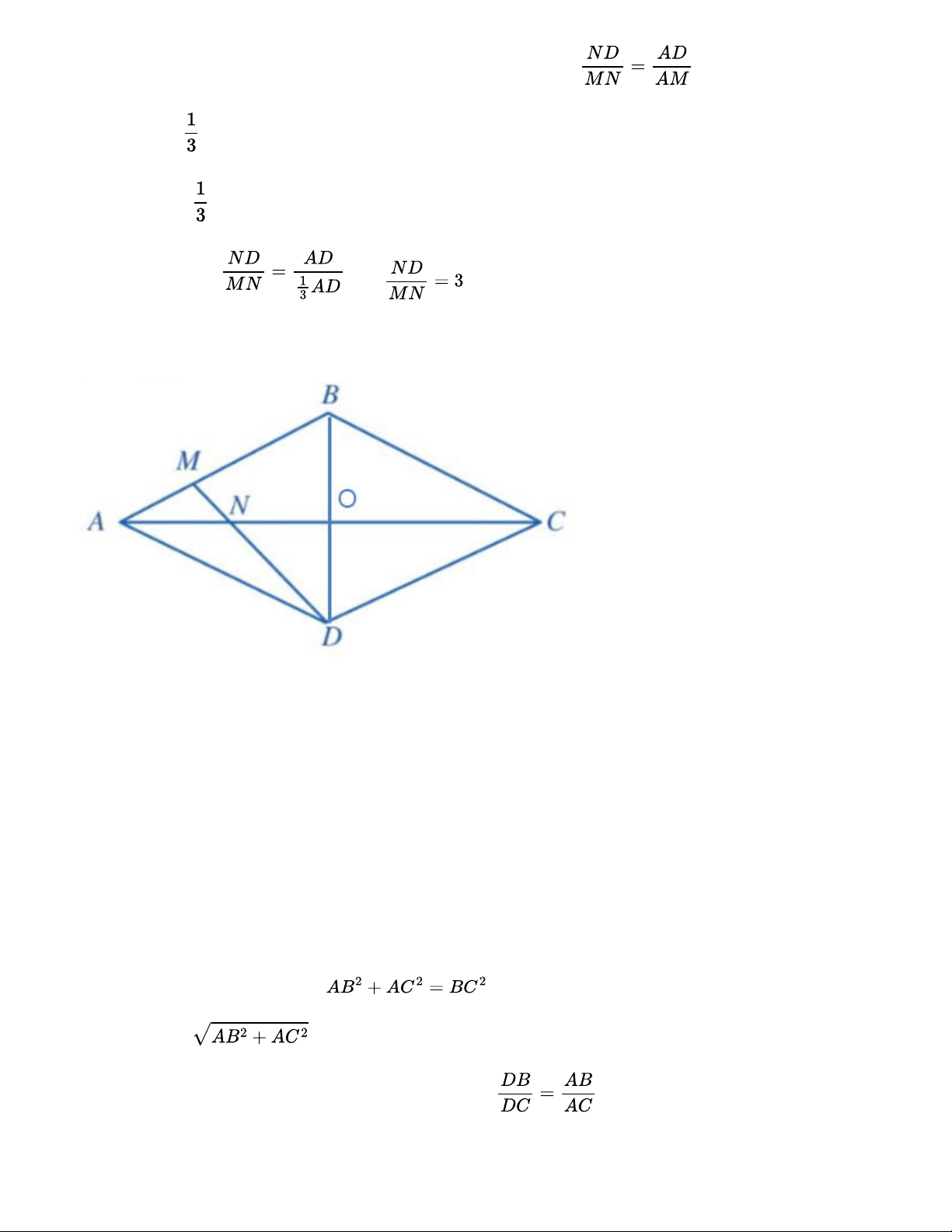
Cho hình thoi ABCD (Hình 44). Điểm M thuộc cạnh AB thỏa mãn AB = 3AM. Hai đoạn thẳng AC
và DM cắt nhau tại N. Chứng minh ND = 3MN. Lời giải:
Gọi giao điểm hai đường chéo AC và BD là O.
Vì ABCD là hình thoi nên AC vuông góc với BD tại O.
Tam giác ABD cân tại A có AO là đường cao nên AO cũng là đường phân giác của góc BAD.
Tam giác AMD có AN là đường phân giác của góc MAD nên (1) Ta có: AM = AB mà AD = AB Suy ra: AM = AD. (2) Từ (1)(2) suy ra: hay . Do đó: ND = 3MN. Bài 5
Cho tam giác ABC vuông tại A có AB = 3, AC = 4, AD là đường phân giác. Tính:
a) Độ dài các đoạn thẳng BC, DB, DC;
b) Khoảng cách từ điểm D đến đường thẳng AC;
c) Độ dài đường phân giác AD. Lời giải:
a) Tam giác ABC vuông tại A: Suy ra: BC = = 5
Do AD là đường phân giác của tam giác ABC nên Mà DC = BC - DB Nên hay Do đó: DB = ; DC = 5 - =
b) Từ D kẻ đường thẳng DE vuông góc với AC. DE là khoảng cách từ D đến đường thẳng AC.
Ta có: DE // AB (cùng vuông góc với AC) Suy ra: hay Do đó: DE = . c) Vì DE // AB nên hay Suy ra: AE = . Tam giác ADE vuông tại E: . Bài 6
Cho tứ giác ABCD với các tia phân giác của các góc CAD và CBD cùng đi qua điểm E thuộc
cạnh CD (Hình 45). Chứng minh AD.BC = AC.BD. Lời giải:
Tam giác ACD có AE là đường phân giác của góc CAD. Suy ra: (1)
Tam giác BCD có BE là đường phân giác của góc CBD. Suy ra: (2) Từ (1)(2) suy ra: hay AD.BC = AC.BD.