















Preview text:
Tuần 2 Tiết 1; 2; 3 Ngày soạn 20/8/2023 Lớp 8A1 8A2 8A3 Ngày dạy:
ÔN TẬP BÀI 1,2: ĐƠN THỨC, ĐA THỨC I. MỤC TIÊU 1. Về kiến thức:
-Học sinh nhận biết được đơn thức, đơn thức thu gọn, hệ số, phần biến và bậc của đơn thức.
-Học sinh thu gọn được được đơn thức, nhận biết được đơn thức đồng dạng và cộng,
trừ hai đơn thức đồng dạng.
-Nhận biết được đa thức, hạng tử của đa thức, đa thức thu gọn.
-Thu gọn được đa thức, tìm được bậc của đa thức.
-Biết tìm giá trị của đa thức khi biết giá trị của biến.
2. Về năng lực: * Năng lực chung:
- Năng lực tự học: HS tự hoàn thành được các nhiệm vụ học tập chuẩn bị ở nhà và tại lớp.
- Năng lực giao tiếp và hợp tác: HS phân công được nhiệm vụ trong nhóm, biết hỗ trợ
nhau, trao đổi, thảo luận, thống nhất được ý kiến trong nhóm để hoàn thành nhiệm vụ.
* Năng lực đặc thù:
- Năng lực giao tiếp toán học: HS phát biểu, nhận biết được đơn thức, đa thức, bậc của đơn thức, đa thức
- Năng lực tư duy và lập luận toán học, năng lực giải quyết vấn đề toán học, năng lực
mô hình hóa toán học: thực hiện được các thao tác tư duy so sánh, phân tích, tổng hợp, tính toán,
3. Về phẩm chất:
- Chăm chỉ: thực hiện đầy đủ các hoạt động học tập một cách tự giác, tích cực.
- Trung thực: thật thà, thẳng thắn trong báo cáo kết quả hoạt động cá nhân
- Trách nhiệm: hoàn thành đầy đủ, có chất lượng các nhiệm vụ học tập.
II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU
1. Giáo viên: SGK, kế hoạch bài dạy, máy chiếu.
2. Học sinh: SGK, vở ghi.
III. TIẾN TRÌNH DẠY HỌC 1. KIẾN THỨC CẦN NHỚ 1) Đơn thức.
Đơn thức là biểu thức đại số chỉ gồm một số hoặc một biến hoặc có dạng tích của những số và biến
2) Đơn thức thu gọn, bậc của một đơn thức. Trang 1
Đơn thức thu gọn là đơn thức chỉ gồm một số hoặc có dạng tích của một số với
những biến, mỗi biến chỉ xuất hiện một lần và đã được nâng lên lũy thừa với số mũ nguyên dương.
Tổng các số mũ của các biến trong một đơn thức thu gọn với hệ số khác 0 gọn
là bậc của đơn thức đó.
Trong một đơn thức thu gọn, phần số còn gọi là hệ số, phần còn lại gọi là phần biến.
VD: Với đơn thức (− )7 3 5
2 x y z thì phần hệ số là ( )7 2 − còn phần biến là 3 5 x y z
Với các đơn thức có hệ số là 1 hay −1 ta không viết số 1. VD: Với đơn thức 5
−x y có hệ số là −1
Mỗi số khác 0 cũng là một đơn thức thu gọn với bậc là 0
Số 0 cũng được gọi là một đơn thức, đơn thức này không có bậc.
3) Đơn thức đồng dạng.
Hai đơn thức đồng dạng là hai đơn thức có hệ số khác 0 và có phần biến giống nhau.
Hai đơn thức đồng dạng thì có cùng bậc.
Để thực hiện phép cộng, trừ các đơn thức đồng dạng, ta cộng, trừ phần hệ số và giữ nguyên phần biến. 4) Đa thức.
Đa thức là tổng của những đơn thức, mỗi đơn thức trong tổng gọi là một hạng tử của đa thức đó.
Mỗi đơn thức cũng được gọi là một đa thức.
5) Thu gọn đa thức.
Đa thức thu gọn là đa thức không có hai hạng tử nào đồng dạng.
Bậc của một đa thức là bậc của hạng tử có bậc cao nhất trong dạng thu gọn của đa thức đó.
Một số khác 0 cũng được coi là một đa thức bậc 0
Số 0 cũng là một đa thức, gọi là đa thức 0 và không có bậc xác định. 2. BÀI TẬP
Hoạt động của giáo viên và học sinh Nội dung * Giao nhiệm vụ
Dạng 1: Nhận biết đơn thức, đơn thức
- GV chiếu bài tập lên máy chiếu yêu cầu
đồng dạng, đa thức, bậc và hệ số của
học sinh trả lời nhanh bài tập trắc nghiệm
đơn thức, đa thức - HS tìm hiểu bài toán 1
Bài 1: Bài tập trắc nghiệm
a) Trong các biểu thức sau, biểu thức nào là đơn thức?
A. 2x − y B. −2 2xy C. 4 x D. xy − 4
b) Trong các biểu thức sau, biểu thức nào là đa thức? x xy
A. 3xy − 6xy B. 1 − 2 C. 3 − y D. 15 − xy + x 2 2
c) Tìm đơn thức đồng dạng với đơn thức 2 −4xy . Trang 2 A. 1 4 − 2 −xy B, 2 4x y C. D. 2 4 − xy 2 xy
d) Hệ số của đơn thức 2 −2 xyz là:
A. 2 B. −2 C. xyz D. −4
*Thực hiện nhiệm vụ
a) Trong các biểu thức sau, biểu thức nào
-GV yêu cầu hS hoạt động cá nhân là đơn thức?
- Giáo viên gọi lần lượt HS đứng tại chỗ A. 2x − y B. −2 2xy trả lời và giải thích
C. 4 x D. xy − 4
HS đứng tại chỗ trả lời các câu hỏi trả lời Ta có: 2x− y , xy−4 là đa thức các câu hỏi a) Đáp án B
4 x không là đơn thức b) Đáp án C
b) Trong các biểu thức sau, biểu thức nào c) Đáp án B là đa thức? d) Đáp án D
A. 3xy − 6xy B. 1 − 2
- HS chốt được kiến thức: Đơn thức là x
biểu thức đại số chỉ gồm một số hoặc một C. x xy 3 − y D. 15 − xy +
biến hoặc có dạng tích của những số và 2 2 biến
Ta có: 3xy − 6xy = 3
− xy là đơn thức 1 1− 2x − 2 = không là đa thức x x xy 29 − 15 − xy + = xy là đơn thức 2 2
c) Tìm đơn thức đồng dạng với đơn thức 2 −4xy . A. 2 −xy B, 2 4x y C. 1 D. 4 − 2 4 − xy 2 xy Ta có đơn thức 2 −4xy và 2 −xy có cùng phần biến 2
xy và hệ số khác 0.
d) Hệ số của đơn thức 2 −2 xyz là:
A. 2 B. −2 C. xyz D. −4 Ta có: 2
−2 = −4 nên đơn thức đó có hệ
*Kết luận, nhận định: số là −4 .
-Tại sao 4 x không là đơn thức?
- Vì biểu thức đó gồm tích của một số với
căn bậc hai của 1 biến. *Giao nhiệm vụ Bài 2:
- GV chiếu bài tập lên máy chiếu, gọi một Phương pháp:
HS đứng tại chỗ đọc đề bài.
-Bước 1: Thu gọn đơn thức. Trang 3
-Một HS đứng tại chỗ đọc đề bài
-Bước 2: Tìm bậc và hệ số của đơn thức.
Bài 2. Tìm bậc và hệ số của các biểu thức đại số sau: a) 4 − xy − 3xy b) 1 3 3 x y − x y 2
c) 2xy + 4xy −8xy d) 2 (−xy).( 5 − x yz) e) 3 2 xy .( 2 − xy) 2
*Thực hiện nhiệm vụ
-GV yêu cầu HS hoạt động cá nhân a) 4 − xy − 3xy -Hs hoạt động cá nhân = ( 4
− − 3)xy = −7xy - Em hãy nêu cách làm?
Đơn thức có hệ số là 7 − , bậc là 2
-Một hS đứng tại chỗ nêu cách làm b) 1 3 3 x y − x y
-Muốn tìm bậc của đơn thức làm như thế 2 nào? 1 1 3 3
( −1)x y = − x y
-Muốn tìm bậc của đơn thức ta cộng số mũ 2 2 của các biến lại.
Đơn thức có hệ số là , bậc là 4
- GV gọi 5 HS lên bảng trình bày
c) 2xy + 4xy −8xy = (2 + 4 −8)xy = 2 − xy
Đơn thức có hệ số là −2 , bậc là 2 d) 2
(−xy).(−5x yz) 2 3 2 = ( 1 − ).(−5).( . x x ).( .
y y).z = 5x y z
Đơn thức có hệ số là 5 , bậc là 6 e) 3 2 xy .( 2 − xy) 2 3 2 2 3 = .( 2 − ).( . x x).( y y) = 3 − x y 2 Đơ thức có hệ số là 3 − , bậc là 5
*Kết luận, nhận định:
- HS khác ở dưới nhận xét
GV chốt phương pháp giải của dạng toán và một số lưu ý
-HS nắm được lưu ý: Trước khi tìm bậc
và hệ số của đơn thức cần thu gọn đơn thức. *Giao nhiệm vụ Bài 3 Trang 4
-GV đưa bài tập lên yêu cầu hoạt động cá Phương pháp: nhân
-Chọn các đơn thức có cùng phần biến với -HS nhận nhiệm vụ
nhau thành một nhóm. Lưu ý cần rút gọn
Bài 3. Phân thành các nhóm đơn thức
đơn thức trước ( nếu cần)
đồng dạng trong các đơn thức sau: 5 4 2 3 3 3 2 x y z −x y 3x y , , 11 6 3 3 −11x y , 5 4 2 6 − x y z , 1 3 2 6 x y . 2
*Thực hiện nhiệm vụ
-HS hoạt động cá nhân, suy nghĩ bài làm 1 N1: 3 2 3x y , 3 2 6 x y -Hãy nêu cách làm? 2
-GV gọi một hS lên bảng trình bày 5 4 2 x y z N2: , 5 4 2 −
-Một HS lên bảng trình bày 6x y z 11
*Kết luận, nhận định 3 3 −x y
-GV chốt kiến thức và lưu ý: Hai đơn thức N3: , 3 3 −11x y 6
đồng dạng thì cùng bậc với nhau nhưng *Lưu ý:
hai đơn thức cùng bậc với nhau thì chưa Hai đơn thức đồng dạng thì cùng bậc với
chắc đã đồng dạng với nhau
nhau nhưng hai đơn thức cùng bậc với
-HS nắm được lưu ý
nhau thì chưa chắc đã đồng dạng với nhau VD: 3 2 3x y và 2 3
6x y có cùng bậc là 5
nhưng không đồng dạng với nhau vì
không cùng phần biến ( 3 2 2 3 x y x y *Giao nhiệm vụ Bài 4.
-GV yêu cầu hS đọc bài toán Phương pháp
-HS đứng tại chỗ đọc bài
-Nhóm các đơn thức đồng dạng với nhau
Bài 4: Thu gọn rồi tìm bậc rồi thu gọn. của các đa thức sau
-Tìm bậc của từng hạng tử ( đơn thức). 6 5 4 4 4 4
A = x + y + x y +1− x y
Đơn thức nào có bậc cao nhất chính là bậc 5 4 của đa thức
B = x − x − + ( 5 7 2 1 7 − x ) 4 2 2 4
C = x − 2x y + 3xy + 5 − x
*Thực hiện nhiệm vụ
-GV yêu cầu hS hoạt động cá nhân -HS hoạt động cá nhân
-Em hãy nêu cách làm? Thế nào là bậc của đa thức?
- Bậc của một đa thức là bậc của hạng tử
có bậc cao nhất trong dạng thu gọn của đa Trang 5 thức đó. 6 5 4 4 4 4
A = x + y + x y +1− x y
-GV gọi 3 HS lên bảng trình bày 6 5 4 4 4 4
= x + y + (x y − x y ) +1 -3 HS lên bảng trình bày 6 5 = x + y +1 ( 6
x có bậc là 6 , 5
y có bậc là 5 , 1 có bậc là 0 )
Đa thức A có bậc là 6 . 5 4
B = x − x − + ( 5 7 2 1 7 − x ) 5 5 4 = 7x + ( 7
− x ) − 2x −1 4 = 2 − x −1 ( 4
−2x có bậc là 4 , 1
− có bậc là 0 ) Đa thức B có bậc là 4 4 2 2 4 = − + + − C x 2x y 3xy 5 x 4 4 2 2
= (x − x ) − 2x y + 3xy + 5 2 2 = 2
− x y + 3xy + 5 ( 2 2
−2x y có bậc là 4 , 3xy có bậc là 2 ,5 có bậc là 0 )
Đa thức C có bậc là 4
*Kết luận, nhận định
-HS khác ở dưới nhận xét
Lưu ý: Trước khi tìm bậc cần thu gọn đa
-GV chốt kiến thức và lưu ý: Trước khi thức
tìm bậc của đa thức cần thu gọn đa thức đó. -HS nắm được lưu ý *GV giao nhiệm vụ
Dạng 2: Thực hiện phép tính
-GV chiếu bài tập lên yêu cầu một hS Bài 5: Bài tập Trắc nghiệm
đứng tại chỗ đọc
-Một HS đứng tại chỗ đọc đề bài
Bài 5. Chọn đáp án đúng
a) Kết quả của phép tính xy − (−xy) + 5xy là:
A. 5xy B. 6xy C. 7xy D. −5xy b) Thực hiện phép tính 2 5xy .( 3
− y)2 được kết quả: A. 2x B. 4 −15xy C. 4 −45xy D. 4 45xy
c) Kết quả của phép tính 2
−xyz − 3xz.yz là: A. 2 −4xyz B. 2 −3xyz C. 2 −xyz D. 2 4xyz
*Thực hiện nhiệm vụ a) Đáp án C Trang 6
-GV yêu cầu HS thực hiện cá nhân trả lời b) Đáp án D nhanh c) Đáp án A - HS thực hiện các nhân
a)Kết quả của phép tính
-Nhắc lại cách cộng, trừ hai đơn thức đồng xy − (−xy) + 5xy là: dạng? A. 5xy B. 6xy
-Muốn cộng, trừ hai đơn thức đồng dạng ta C. 7xy D. −5xy
cộn, trừ các hệ số với nhau và giữ nguyên Ta có: xy −(−xy)+5xy phần biến
-GV gọi lần lượt hS đứng tại chỗ trả lời = 7xy
-3 HS lần lượt đứng tại chỗ trả lời b) Thực hiện phép tính -Hãy nêu cách làm ý c) 2 5xy .( 3
− y)2 được kết quả: -Bước 1: Tính 2 3x . z yz = 3xyz A. 2x B. 4 −15xy
-Bước 2: Trừ hai đơn thức đồng dạng C. 4 −45xy D. 4 45xy Ta có: 2 5xy .( 3 − y)2 2 2 = 5xy .9 y 4 = 45xy
c) Kết quả của phép tính 2
−xyz − 3xz.yz là: A. 2 −4xyz B. 2 −3xyz C. 2 −xyz D. 2 4xyz
*Kết luận, nhận định Ta có: 2
−xyz − 3xz.yz -HS khác nhận xét 2 2
= −xyz − 3xyz 2 = 4 − xyz
-GV nhận xét và chốt kiến thức *GV giao nhiệm vụ
Bài 6: Thực hiện phép tính -GV chiếu bài tập lên Phương pháp: -HS đọc đề bài
-Bước 1: Thu gọn các hạng tử
Bài 6: Thực hiện phép tính:
-Bước 2: Nhóm các hệ số với nhau và giữ a) 2 8 − x y − . x (xy)
nguyên phần biến(Nếu đơn thức đồng b) 2 dạng) xy x − ( 2 2 4 . 1 − 2x y ) 5 c) 3xy ( 2 x y) 3 2 − x y 6 d) 4 4 2 2
15x + 7x − 20x .x
*Thực hiện nhiệm vụ
-GV yêu cầu hS hoạt động cặp đôi
-HS hoạt động cặp đôi -Hãy nêu cách làm? a) 2 8 − x y − . x (xy) -Một HS nêu cách làm 2 2 = 8
− x y − x y
-GV gọi đại diện của 4 cặp nhanh nhất lên Trang 7 trình bày 2 = ( 8 − −1)x y 2 = 9 − x y -4 HS lên bảng trình bày b) 2 xy x − ( 2 2 4 . 1 − 2x y ) 2 2 2 2 = 4x y +12x y 2 2 = 16x y 5 c) 3xy ( 2 x y) 3 2 − x y 6 3 2 5 3 2 = − 3x y x y 6 5 3 2 13 3 2 = 3 − x y = x y 6 6 d) 4 4 2 2
15x + 7x − 20x .x 4 4 4
*Kết luận, nhận định
= (15x + 7x ) − 20x -HS khác nhận xét 4 = (15 + 7 − 20)x 4 = 2x
-GV nhận xét và chốt kiến thức. *Giao nhiệm vụ Bài 7:
-GV yêu cầu hS đọc bài toán Phương pháp
-Một HS đứng tại chỗ đọc bài toán
Bước 1: Chuyển các hạng tử sang vế phải
Bài 7: Tìm hiệu A − B biết
Bước 2: Áp dụng qui tắc công, trừ đa thức a) 2 2 2 2
−x y + A + 2xy − B = 3x y − 4xy để thu gọn vế phải − b) 2 2 2 2 Bước 3: Tìm A B
5xy − A − 6yx + B = 7 − xy + 8x y c) 2 3 3 2 2 3 3 2
3x y − A − 5x y + B = 8x y − 4x y
*Thực hiện nhiệm vụ
-GV yêu cầu hS hoạt động theo bàn -HS thực hiện theo bàn
-Một em đại diện nêu cách làm?
-Một hS đứng tại chỗ nêu cách làm:
B1: Chuyển các hạng tử sang vế phải
B2: Áp dụng qui tắc công, trừ đa thức để thu gọn vế phải
B3: Tìm A − B
-GV gọi đại diện 3 bàn nhanh nhất lên bảng -3 HS lên bảng trình bày
-Để làm bài tập này em cần áp dụng những a) 2 2 2 2
−x y + A + 2xy − B = 3x y − 4xy
kiến thức nào đã học? 2 2 2 2 − = − + −
-HS: -Cần áp dụng quy tắc chuyển vế, A B 3x y 4xy x y 2xy
cách cộng, trừ hai đơn thức và quy tắc dấu 2 2 2 2
= (3x y + x y) − (4xy + 2xy )
ngoặc (theo chiều ngược lại) 2 2 = 4x y − 6xy Trang 8 b) 2 2 2 2
5xy − A − 6yx + B = 7 − xy + 8x y 2 2 2 2 −A + B = 7
− xy + 8x y − 5xy + 6x y 2 2 2 2 = − − + + ( 7xy
5xy ) (8x y 6x y) 2 2 = 12 − xy +14x y Suy ra
A − B = −(− A + B) 2 2 = −( 1 − 2xy +14x y) 2 2
= 12xy −14x y c) 2 3 3 2 2 3 3 2
3x y − A − 5x y + B = 8x y − 4x y 2 3 3 2 2 3 3 2
−A + B = 8x y − 4x y − 3x y + 5x y 2 3 2 3 3 2 3 2
= (8x y − 3x y ) + (5x y − 4x y ) 2 3 3 2 = 5x y + x y
Sy ra: A − B = −(− A + B) 2 3 3 2
= −(5x y + x y ) 2 3 3 2 = 5
− x y − x y *Lưu ý:
*Kết luận, nhận định
A − B = −(− A + B)
-Các HS ở dưới nhận xét
-GV nhận xét và chốt kiến thức
-Hãy nhắc lại qui tắc chuyển vế ?
-Một HS đứng tại chỗ nhắc lại qui tác chuyển vế.
-GV lưu ý: A − B = −(− A + B) * Giao nhiệm vụ
Dạng 3: Toán tổng hợp - GV chiếu bài tập lên
Bài 8: Bài tập trắc nghiệm
-Một HS đứng tại chỗ đọc bài
-Một HS đứng tại chỗ đọc bài
-Các HS khác tìm hiểu bài toán Bài 8. Cho đa thức 6 5 4 4 4 4
A = x + y + x y +1− x y
a) Thu gọn đa thức được kết quả: A. 6 5
x + y + xy +1 B. 6 5 0 0
x + y + x y +1 C. 6 5
A = x + y +1 D. 6 5 4 4
A = x + y + 2x y +1
b) Bậc của đa thức là: Trang 9 A.1 B. 2 C. 5 D. 6
c) Giá trị của đa thức tại x = 1, y = −1 là: A.1 B. 2 C. 3 D. 4
*Thực hiện nhiệm vụ
-GV yêu cầu hS hoạt động cá nhân -HS hoạt động cá nhân
-Hãy nêu cách thu gọn đa thức?
a)Thu gọn đa thức được kết quả:
-Muốn thu gọn đa thức ta nhóm các hạng A. 6 5
x + y + xy +1
tử( đơn thức) đồng dạng với nhau B. 6 5 0 0
x + y + x y +1
-Thế nào là bậc của đa thức? C. 6 5 = + +
-Bậc của đa thức là bậc của hạng tử có bậc A x y 1 cao nhất D. 6 5 4 4
A = x + y + 2x y +1
-Muốn tính giá trị của đa thức em làm như Ta có: nào? 6 5 4 4 4 4
A = x + y + x y +1− x y
-Ta thay giá trị của biến vào đa thức 6 5 4 4 4 4
= x + y + (x y − x y ) +1
-GV gọi các hS đứng tại chỗ trả lời nhanh 6 5 = x + y +1
-3 HS đứng tại chỗ trả lời nhanh a) Đáp án C Đáp án C b) Đáp án D b)Bậc của đa thức là: c) Đáp án A A.1 B. 2 C. 5 D. 6 Ta có: 6 x có bậc là 6 5 y có bậc là 5 1 có bậc là 0
Vậy đa thức có bậc là 6 Đáp án D.
c) Giá trị của đa thức tại x = 1, y = −1 là: A.1 B. 2 C. 3 D. 4
Thay x = 1, y = −1 vào đa thức 6 5
x + y +1ta được 6 5 A = 1 + ( 1 − ) +1 A = 1−1+1 = 1
*Kết luận, nhận định Đáp án A -Các hS khác nhận xét
*Lưu ý: Trước khi tìm bậc của đa thức -GV nhận xét và lưu ý:
cần thu gọn đa thức.
Trước khi tìm bậc của đa thức cần thu gọn đa thức -HS nắm lưu ý Trang 10 *Giao nhiệm vụ Bài 9.
-GV yêu cầu hS đọc đề bài Phương pháp: -HS tìm hiểu đề bài
Bước 1: Áp dụng qui tắc nhân hai đơn 3 − thức
Bài 9: Cho hai đơn thức 3 2 x y z và 2
Bước 2: Thu gọn đơn thức ( 3 5 6 − xy z ).
Bước 3: Tìm hệ số (phần số), phần biến
a)Tính tích hai đơn thức trên
và bậc (tổng số mũ của các biến)
b)Chỉ ra hệ số, phần biến và bậc của đơn thức tích.
*Thực hiện nhiệm vụ
-GV yêu cầu hS hoạt động cá nhân -HS hoạt động cá nhân
-Muốn nhân hai đơn thức em làm như thế nào?
-Muốn nhân hai đơn thức em nhân hệ số
với hệ số, nhận phần biến với phần biến -Hãy nêu các bước làm? -Một HS nêu cách làm
-GV gọi hai HS lên bảng(mỗi HS một ý) -HS lên bảng trình bày 3 − a) 3 2 3 5 x y . z ( 6 − xy z ) 2 3 − 3 2 3 5 = [( ).( 6 − )].(x y . z xy z ) 2 4 5 6 = 9x y z b)Hệ số: 9 Phần biến: 4 5 6 x y z Bậc: 4 + 5 + 6 = 15
*Kết luận, nhận định -HS khác nhận xét
-GV nhận xét và chốt kiến thức
-GV lưu ý cho HS: Đối với đơn thức có
dạng xy hoặc −xy thì hệ số là 1 hoặc 1
− *Lưu ý: Đối với đơn thức có dạng xy
.(nhiều hS cho hệ số bằng 0 là sai)
hoặc −xy thì hệ số là 1 hoặc 1 − -HS nắm lưu ý *Giao nhiệm vụ Bài 10.
-GV chiếu bài tập lên và yêu cầu HS đọc Phương pháp bài
Bước 1: Nhóm các đơn thức đồng dạn
-Một HS đọc bài, cả lớp tìm hiểu bài với nhau
Bài 10: Thu gọn, tìm bậc rồi tính giá trị
Bước 2: Thu gọn đa thức Trang 11 của các đa thức sau
Bước 3: Tìm bậc của đa thức 1 2 2 1 2 1 2
A = x y + xy − xy + xy − 5xy − x y Bước 4: Thay giá trị của x, y vào đa thức 3 2 3
trên ta được giá trị cần tìm 1
Tại x = , y =1 2 1 2 2 2 2
B = xy + x y − xy + xy 2 3 1 2 − x y + 2xy 3 1
tại x = , y =1 2
*Thực hiện nhiệm vụ
-GV yêu cầu HS hoạt động cá nhân -HS hoạt động cá nhân
?Muốn thu gọn đa thức em làm như thế nào?
-Muốn thu gọn đa thức ta nhóm các hạng
tử (đơn thức) đồng dạng với nhau. 1
-Một em hãy nêu cách làm 2 2
A = x y + xy − xy 3 -Một hS nêu cách làm 1 2 1 2
-GV gọi hai HS lên bảng trình bày
+ xy − 5xy − x y 2 3 -Hai HS lên bảng. 1 2 1 2
= ( x y − x y) + 3 3 2 1 2
(xy + xy ) − (xy + 5xy) 2 3 2
= xy − 6xy 2 -Bậc của đa thức là 3 1
Tại x = , y =1thì 2 3 1 2 1 A = . .1 − 6. .1 2 2 2 9 A = − 4 1 2 2 2
B = xy + x y − xy 2 3 2 1 2
+xy − x y + 2xy 3 Trang 12 1 2 2
B = ( xy + xy ) + 2 2 2 1 2
( x y − x y) − (xy − 2xy) 3 3 3 2 1 2
B = xy + x y + xy 2 3 1
Tại x = , y =1thì 2 2 3 1 2 1 1 1 = + + B . .1 . .1 .1 2 2 3 2 2 4
*Kết luận, nhận định B = 3
-Hai HS đứng tại chỗ nhận xét
-GV nhận xét và chốt kiến thức -HS lắng nghe
IV. PHIẾU BÀI TẬP BỔ TRỢ 1. TRẮC NGHIỆM
Câu 1. Trong các biểu thức sau, biểu thức nào là đơn thức? 1 1 A. 2 x y B. −3x −1 C. 2 − x y D. 5 6 − x
Câu 2. Trong các biểu thức sau, biểu thức nào là đơn thức? 6 2 −x y 4 − 1 A. B. C. D. ( 2 x − ) 1 2 x 2 xy z 5 2
Câu 3. Phần hệ số và bậc của các đơn thức 2 5
−x y .(−xy) là: A. −1;7 B. −1;9 C.1;7 D.1;9 2
Câu 4. Kết quả thu gọn của đơn thức 3 2
−xy − y .xy là: 7 9 9 9 9 A. 3 − xy B. 3 xy C. 3 − x y D. 3 x y 7 7 7 7
Câu 5. Trong các biểu thức sau, đâu là đa thức 1 x + 2 y A. 2 x y B. C. D. x + 2 y x 2 z
Câu 6. Trong các biểu thức sau, đâu không là đa thức 1 x x + 2y 1 A. 2 xy − B. C. 6 − 2xy + D. 0 2 3 5 2 x
Câu 7. Bậc của các đa thức ( − )2 2 1 x là: A. 2 B. 3 C. 4 D. 5 2. TỰ LUẬN Trang 13
Bài 1: Phân thành các nhóm đơn thức đồng dạng trong các đơn thức sau: 1 2 3 −12x y − xyz −100 −3yxz −2xy.x . y − xy 8 3
Bài 2: Thực hiện phép tính:
1) xy − (−xy) + 5xy 2) 2 2 2
6xy − 3xy −12xy 3) 2 3 4 x y z + ( 2 3 4 3 4 − x y z ) 4) 2 x y + ( 2 4 8 − x y) 5) 2 x y + ( 2 25 5 − 5x y) 6) 2 2 2
3x y + 4x y − x y 7) 2 2 xy + x y + ( 2 2 − xy ) 8) 2 3 4 x y z + ( 2 3 4 12 7 − x y z ) 9) 3 − xy − ( 3 − xy ) 3 6 6 + 6x y 8 1 −
Bài 3: Cho đơn thức: 2 2 2 A = x y . x y . 3 4
a) Thu gọn đơn thức A rồi xác định hệ số và tìm bậc của đơn thức.
b) Tính giá trị của A tại x = −1, y = 1. 3 − 7
Bài 4: Cho đơn thức 2 2 2 D = x y x y . 7 9
a) Thu gọn đơn thức D rồi xác định hệ số và phần biến của đơn thức.
b) Tính giá trị của đơn thức D tại x = −1, y = 2 . 2 3 − 20
Bài 5: Cho đơn thức 2 3 F = xy . x y 5 27
a) Thu gọn đơn thức và tìm bậc của đơn thức F −x
b) Tính giá trị của biểu thức F biết y =
và x + y = 2 . 3
Bài 6: Thu gọn rồi tìm bậc của các đa thức sau 1) 2 2 2 2 2
A = 5x .2y − 5 .3
x xy − x y + 6x y 2) 4 3 2 3 2 2 B = 3 . x x + 4 .
x x − 5x x − 5x .x 3) 2 2 2 2
C = 2x yz + 4xy z − 5x yz + xy z − xyz 4) 3 2 2 2 3 2 2 3 2
D = 5x y + 4x y − x + 8x y − 5x y 1 1 1 1 3 3 5) 2 2
E = 3x y − xy +1− 3x y + xy − xy 6) 5 2 2 5 2
F = 3x − x y − xy − 3x − x y 4 2 4 2 4 4 1 1 7) 3 3 2 2
G = x − 5xy + 3x + xy − x + xy − x 8) 5 6 7 2 5 6 7
H = 3xy − 3x y + x y − 3xy + 3x y 2 2 2
Bài 7: Cho hai đơn thức: 3 4 5 A = 18
− x y z và B = x ( yz )2 5 2 . 9
a) Đơn thức C là tích của đơn thức A và B. Xác định phần biến, phần hệ số, bậc của C .
b) Tính giá trị của đơn thức C khi x = 1
− , y =1, z = 1 − .
Bài 8: Thu gọn rồi tính giá trị của các đa thức sau a) 5 3 4 3 4 3 5 3
B = 3x y − 4x y + 2x y − 3x y tại x = 1; y = 2 − b) 2 4 2 2 4 9
C = 2x y + 4xyz − 2x − 5 + 3x y − 4xyz + 3 − y tại x = 1, y = −1 Tuần 3 Tiết 4; 5; 6 Trang 14 Ngày soạn 01/11/2023 Lớp 8A1 8A2 8A3 Ngày dạy:
ÔN TẬP TỨ GIÁC LỒI . HÌNH THANG CÂN I. MỤC TIÊU
1. Về kiến thức:
- Củng cố định nghĩa tứ giác, hình thang, hình thang cân.
- Củng cố các định lí về tổng các góc trong của tứ giác, tính chất của hình thang cân 2. Về năng lực:
- Nhận biết và giải thích được tứ giác là hình thang, hình thang cân
- Lập luận và chứng minh hình học trong những trường hợp đơn giản. * Năng lực chung:
- Năng lực tự học: HS tự hoàn thành được các nhiệm vụ học tập chuẩn bị ở nhà và tại lớp.
- Năng lực giao tiếp và hợp tác: HS phân công được nhiệm vụ trong nhóm, biết hỗ trợ
nhau, trao đổi, thảo luận, thống nhất được ý kiến trong nhóm để hoàn thành nhiệm vụ.
* Năng lực đặc thù:
- Năng lực giao tiếp toán học: HS phát biểu, nhận biết được tứ giác là hình thang, hình thang cân.
- Năng lực tư duy và lập luận toán học, năng lực giải quyết vấn đề toán học, năng lực
mô hình hóa toán học: thực hiện được các thao tác tư duy so sánh, phân tích, tổng hợp
khi làm các bài tập về hình thang, hình thang cân.
3. Về phẩm chất:
- Chăm chỉ: thực hiện đầy đủ các hoạt động học tập một cách tự giác, tích cực.
- Trung thực: thật thà, thẳng thắn trong báo cáo kết quả hoạt động cá nhân và theo
nhóm, trong đánh giá và tự đánh giá.
- Trách nhiệm: hoàn thành đầy đủ, có chất lượng các nhiệm vụ học tập.
II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU
1. Giáo viên: SGK, kế hoạch bài dạy, thước thẳng, bảng phụ hoặc máy chiếu.
2. Học sinh: SGK, thước thẳng, bảng nhóm.
III. TIẾN TRÌNH DẠY HỌC
1. KIẾN THỨC CẦN NHỚ Trang 15
1. Tứ giác, tứ giác lồi a) Định nghĩa
+ Tứ giác ABCD là một hình gồm bốn đoạn thẳng AB , BC , CD , DA trong đó
không có hai đoạn thẳng nào cùng nằm trên một đường thẳng.
+ Tứ giác lồi là tứ giác mà hai đỉnh thuộc một cạnh bất kì luôn nằm về một phía của
đường thẳng đi qua hai đỉnh còn lại.
b) Định lý tổng các góc của một tứ giác:
Tổng các góc của một tứ giác bằng o 360 .
2. Hình thang, hình thang cân
a) Hình thang: Hình thang là tứ giác có hai cạnh đối song song. A B D C -Nhận xét:
+ Hai góc kề một cạnh bên của hình thang có tổng bằng o 180 .
b) Hình thang cân: Hình thang cân là hình thang có hai góc kề một đáy bằng nhau. B A D C - Tính chất:
+ Trong hình thang cân, hai cạnh bên bằng nhau.
+ Trong hình thang cân, hai đường chéo bằng nhau. - Dấu hiệu nhận biết:
+ Hình thang có hai góc kề một đáy bằng nhau thì hình thang đó là hình thang cân.
+ Hình thang có hai đường chéo bằng nhau thì hình thang đó là hình thang cân. 2. BÀI TẬP
Hoạt động của giáo viên và HS Nội dung * Giao nhiệm vụ
Bài 1: Bài tập trắc nghiệm
- GV yêu cầu HS hoạt động cá nhân thực hiện Trang 16 bài tập trắc nghiệm 1. Đáp án:
Kiểm tra củng cố lý thuyết cho HS
- HS nhận nhiệm vụ được giao 1 2 3 4 5
Câu 1 . Các góc của tứ giác có thể là: C B C A A
A. Bốn góc nhọn.
B. Bốn góc tù.
C. Bốn góc vuông.
D. Một góc vuông và ba góc nhọn.
Câu 2. Hình thang là tứ giác có:
A. Hai cạnh đối bằng nhau.
B. Hai cạnh đối song song với nhau.
C. Một góc vuông.
D. Hai đường chéo bằng nhau.
Câu 3. Khẳng định nào sau đây là sai:
A. Tổng các góc của một tứ giác bằng o 360
B. Tổng các góc của hình thang bằng o 360 .
C. Hình thang có các góc đối bằng nhau.
D. Hình thang có hai góc kề cạnh bên bù nhau.
Câu 4. Hình thang cân là hình thang có:
A. Hai góc kề một cạnh đáy bằng nhau.
B. Hai góc đối bằng nhau.
C. Hai cạnh bên song song.
D. Hai cạnh bên bằng nhau
Câu 5 Số đo các góc của tứ giác ABCD theo
tỉ lệ: A : B : C : D = 4 : 3 : 2 :1
Số đo các góc theo thứ tự đó là: A. o o o o 120 ;90 ;60 ;30 . B. o o o o 140 ;105 ;70 ;35 . C. o o o o 144 ;108 ;72 ;36 . Trang 17 D. Cả ,
A B,C đều sai.
*Thực hiện nhiệm vụ
- Giáo viên hướng dẫn HS thực hiện
GV: Cho HS đọc đầu bài trắc nghiệm trên màn hình .
- GV yêu cầu HS hoạt động nhóm đôi thực
hiện bài tập trắc nghiệm 1
- HS HĐ cá nhân thực hiện bài 1. - HS báo cáo kết quả.
- Nhận xét, đánh giá câu trả lời của nhau.
GV: Để chọn phương án đúng ở câu 1,2,3,4,5
ta dựa vào kiến thức nào đã học ? * Giao nhiệm vụ
Dạng 1: Tính các góc của tứ giác, hình
- GV tổ chức hoạt động, hướng dẫn HS tìm thang hiểu bài toán 2:
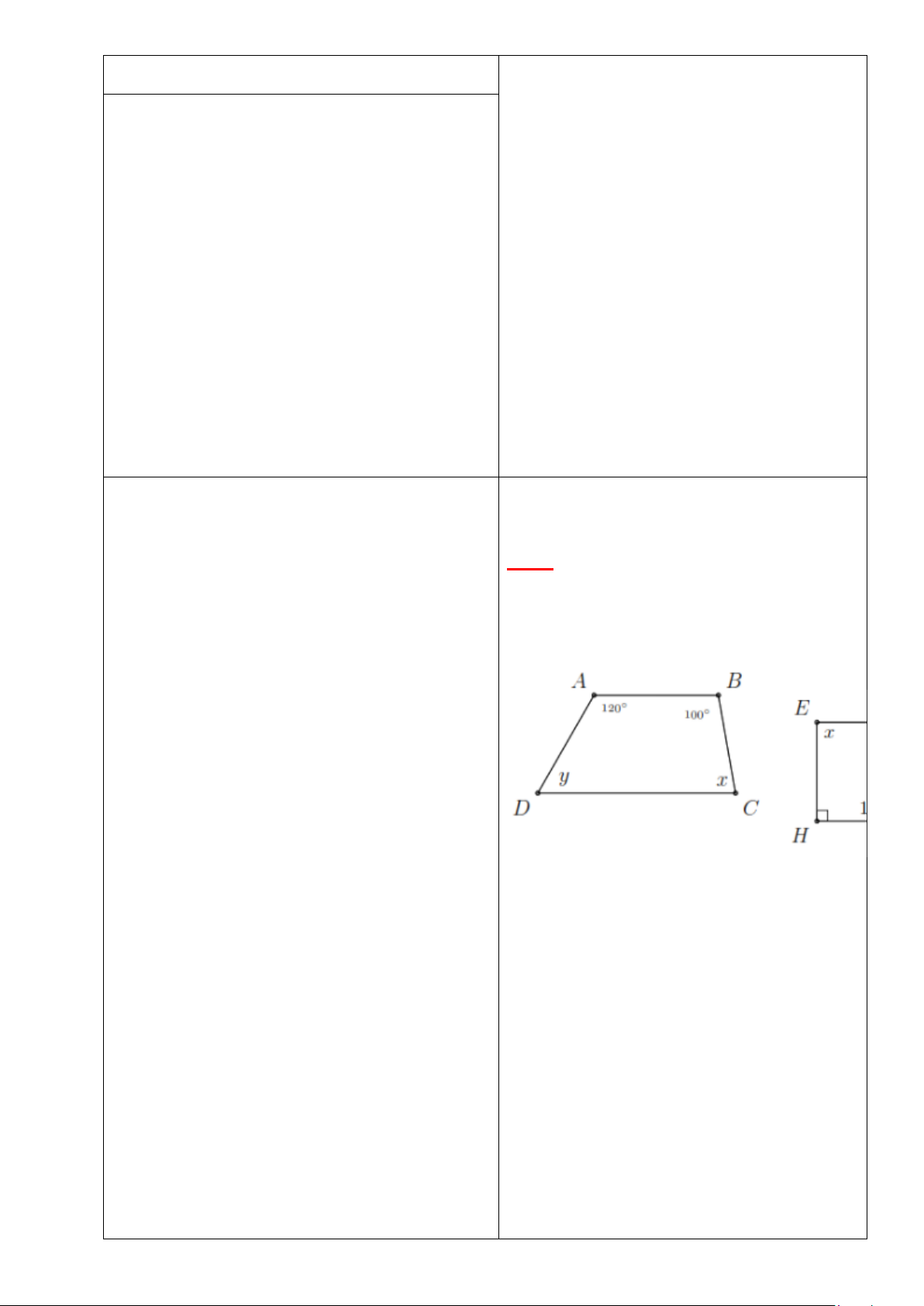
Bài 2: Tìm x và y ở hình vẽ dưới biết
Tìm x và y ở hình vẽ dưới biết các hình các hình thang ABCD và EFGH có đáy
thang ABCD và EFGH có đáy lần lượt là lần lượt là AB và CD ; EF và GH .
AB và CD ; EF và GH - HS tìm hiểu bài toán 2. HS: Đọc đầu bài 2
.*Thực hiện nhiệm vụ
- Giáo viên hướng dẫn HS thực hiện.
GV: Nêu cách tính các góc x và y .
GV: Áp dụng kiến thức nào đã học? Lời giải
HS: Áp dụng tính chất của hai đường thẳng
a) Vì AB // CD nên A + D = 180 hay
song song và tổng các góc trong tứ giác
D +120 = 180 D = y = 60 .
HS: Hoạt động trình bày tính góc HS: Lên bảng trình bày.
Tương tự, B + C = 180 GV: Gọi HS nhận xét
C = x =180 −100 = 80
*Kết luận, nhận định: Khi có giả thiết hình
c) Vì EF // HG nên E + H = 180 .
thang, các em ghi nhớ tính chất của các góc kề
cạnh bên, tổng các góc trong tứ giác bằng E = x = 180 − 90 = 90 360
Tương tự F + G = 180 . Trang 18
F = y = 180 − G = 50 * Giao nhiệm vụ
Bài 3: Cho hình thang ABCD
- GV tổ chức hoạt động, hướng dẫn HS tìm
( AB // CD ) có B − C = 10 hiểu bài toán 3
Tính số đo góc B ? Cho hình thang ABCD Lời giải
( AB // CD ) có B − C = 10
Vì ABCD là hình thang có
Tính số đo góc B ?
AB // CD nên B + C = 180
- HS tìm hiểu bài toán 3.
Và theo GT B − C = 10 HS: Đọc đầu bài 3 180 +10
.*Thực hiện nhiệm vụ B = = 95 2
- Giáo viên hướng dẫn HS thực hiện.
GV: Nêu cách tính góc B
GV: Áp dụng kiến thức nào đã học?
- HS trả lời theo từng câu hỏi được GV đề xuất.
- HS phản biện câu trả lời của nhau.
*Kết luận, nhận định: Khi có giả thiết hình
thang, các em ghi nhớ tính chất của các góc kề
cạnh bên, tìm hai góc khi biết tổng và hiệu của hai góc Dạng 2
Dạng 2: Chứng minh tứ giác là hình * Giao nhiệm vụ
thang, hình thang cân
- GV tổ chức hoạt động, hướng dẫn HS tìm Bài 4: hiểu bài toán 4:
Tứ giác ABCD có BC = CD và DB là
Tứ giác ABCD có BC = CD và DB là phân phân giác của góc D . Chứng minh ABCD
giác của góc D . Chứng minh ABCD là hình là hình thang. thang. Lời giải
HS tìm hiểu bài toán 4
*Thực hiện nhiệm vụ
- Giáo viên hướng dẫn HS thực hiện
GV: Hình vẽ cho biết yếu tố nào bằng nhau? Trang 19 HS quan sát hình vẽ Xét BCD
GV: Dự đoán đáy của hình thang và chứng Có BC = CD nên BCD cân tại C
minh BC // AD như thế nào? Áp dụng kiến suy ra DBC = BDC thức nào đã học?
Mà DB là phân giác của D
HS: dự đoán BC // AD
HS: Chứng minh hai góc so le trong bằng nên CDB = BDA. nhau qua góc khác.
Suy ra ADB = DBC (= CDB)
*Kết luận, nhận định: cách chứng minh tứ nên BC // AD hay ABCD là hình thang.
giác là hình thang: cần tìm một cặp cạnh song song * Giao nhiệm vụ
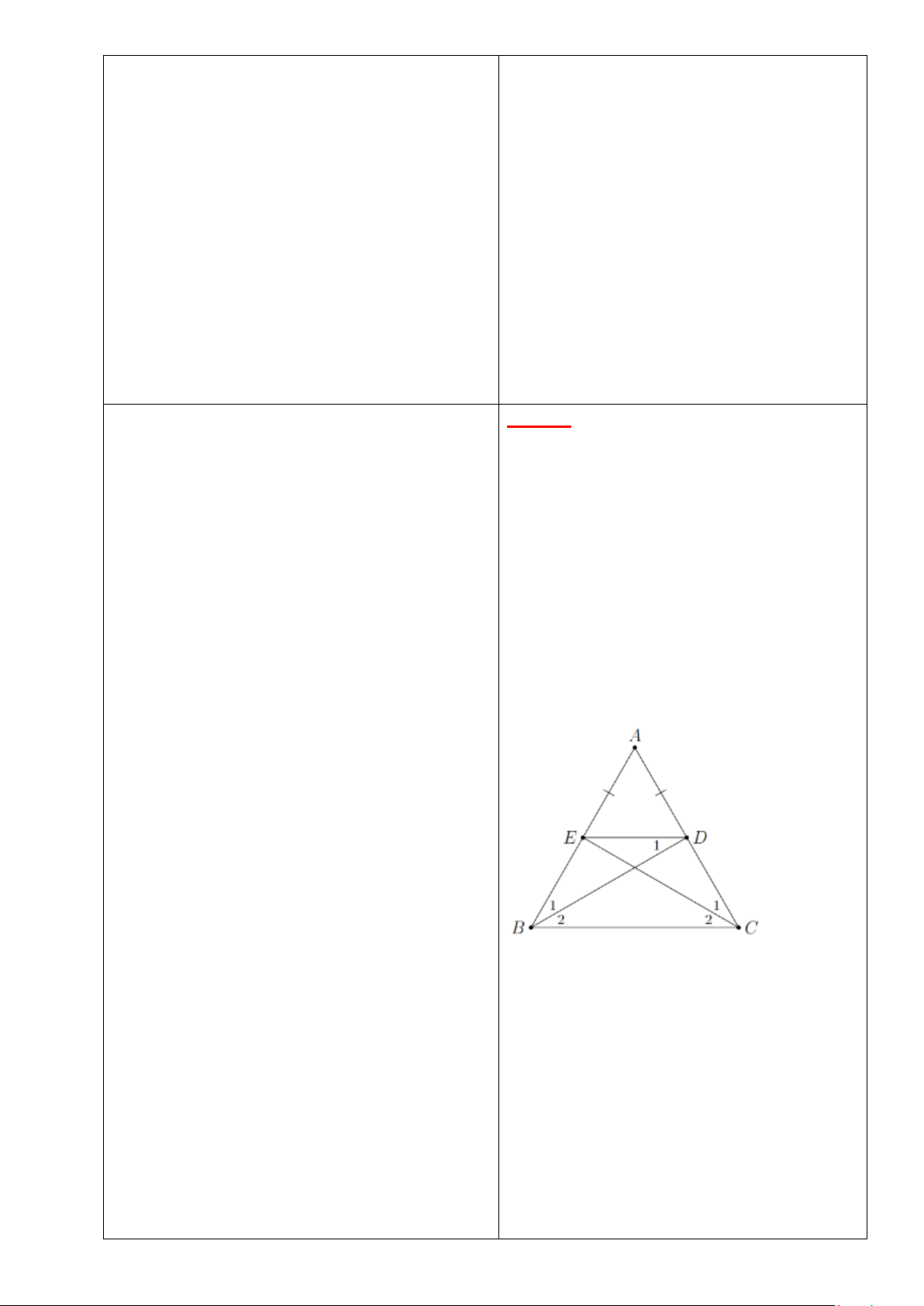
Bài 5: Cho tam giác ABC cân tại A , các
- GV tổ chức hoạt động, hướng dẫn HS tìm
đường phân giác BD , CE hiểu bài toán 5
( D AC , E AB ).
* Thực hiện nhiệm vụ
a) Chứng minh BEDC là hình thang cân;
- Giáo viên hướng dẫn HS thực hiện
b) Tính các góc của hình thang cân BEDC HS thực hiện NV GV giao , biết C = 50 .
GV: Nêu cách nhận biết hình thang cân
GV: Yêu cầu HS hoạt động tìm ra những đk Lời giải
để khẳng định tứ giác là hình thang cân
HS: Để chứng minh tứ giác là hình thang cân
cần chứng minh: hai cạnh đáy song song và
hai góc kề đáy bằng nhau
HS hoạt động theo yêu cầu của GV. HS: Lên bảng trình bày GV: gọi HS nhận xét.
*Kết luận, nhận định: Dấu hiệu nhận biết HTC
a) Do ABC cân tại A và BD , CE là các
Bước 1. Chứng minh hai cạnh đối song song
đường phân giác suy ra hai tam giác BCE
Bước 2. Chứng minh hai góc kề đáy bằng và CDB có
nhau hoặc hai đường chéo bằng nhau ▪ EBC = DCB ,
- Nêu tính chất về góc trong hình thang cân ▪ BC chung, = ▪ BCE DBC . = Vậy BCE CBD (g.c.g). Trang 20




