Giáo án điện tử Toán 10 Chân trời sáng tạo: Hệ thức lượng trong tam giác

Chương ⓶:
§➌ CÁC HỆ THỨC LƯỢNG TRONG TAM GIÁC ⓵. Tóm tắt lý Nội thuyết dung bài
⓶. Phân dạng bài tập học
⓷. Bài tập minh họa FB: Duong Hung ⓵ Tóm T t ắt lý thuy u ết
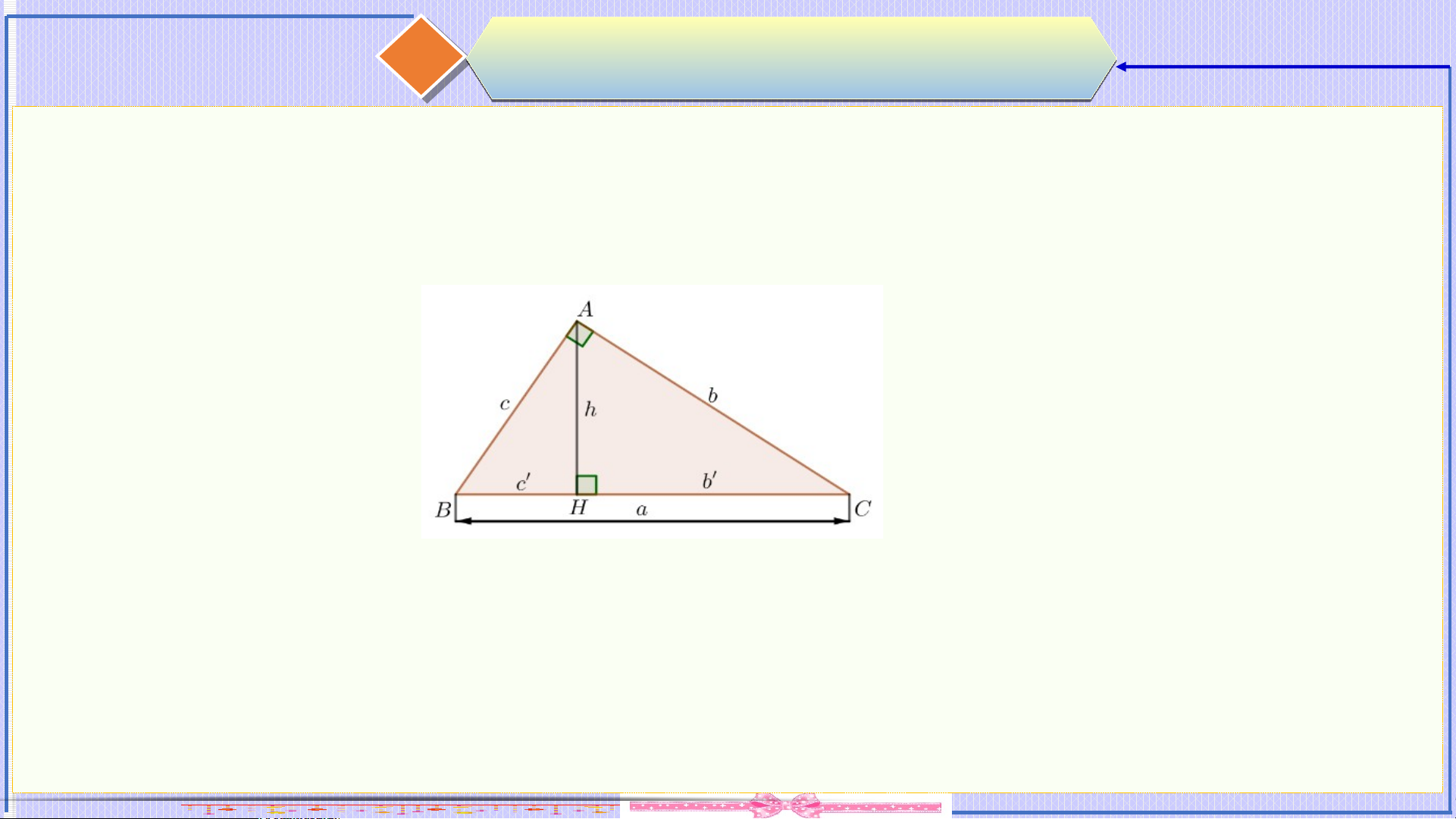
➊. Hệ thức lượng trong tam giác vuông
 Cho tam giác vuông tại đường cao .  Gọi và .  Ta có: 1. 2. 3. 4. 5. 6. 7. 8. 9. ⓵ Tóm T t ắt lý thuy u ết ➋. Tính chất:
. Định lý cosin: Cho tam giác ta có:   
. Hệ quả:    ⓵ Tóm T t ắt lý thuy u ết ➋. Tính chất: . Áp dụng:
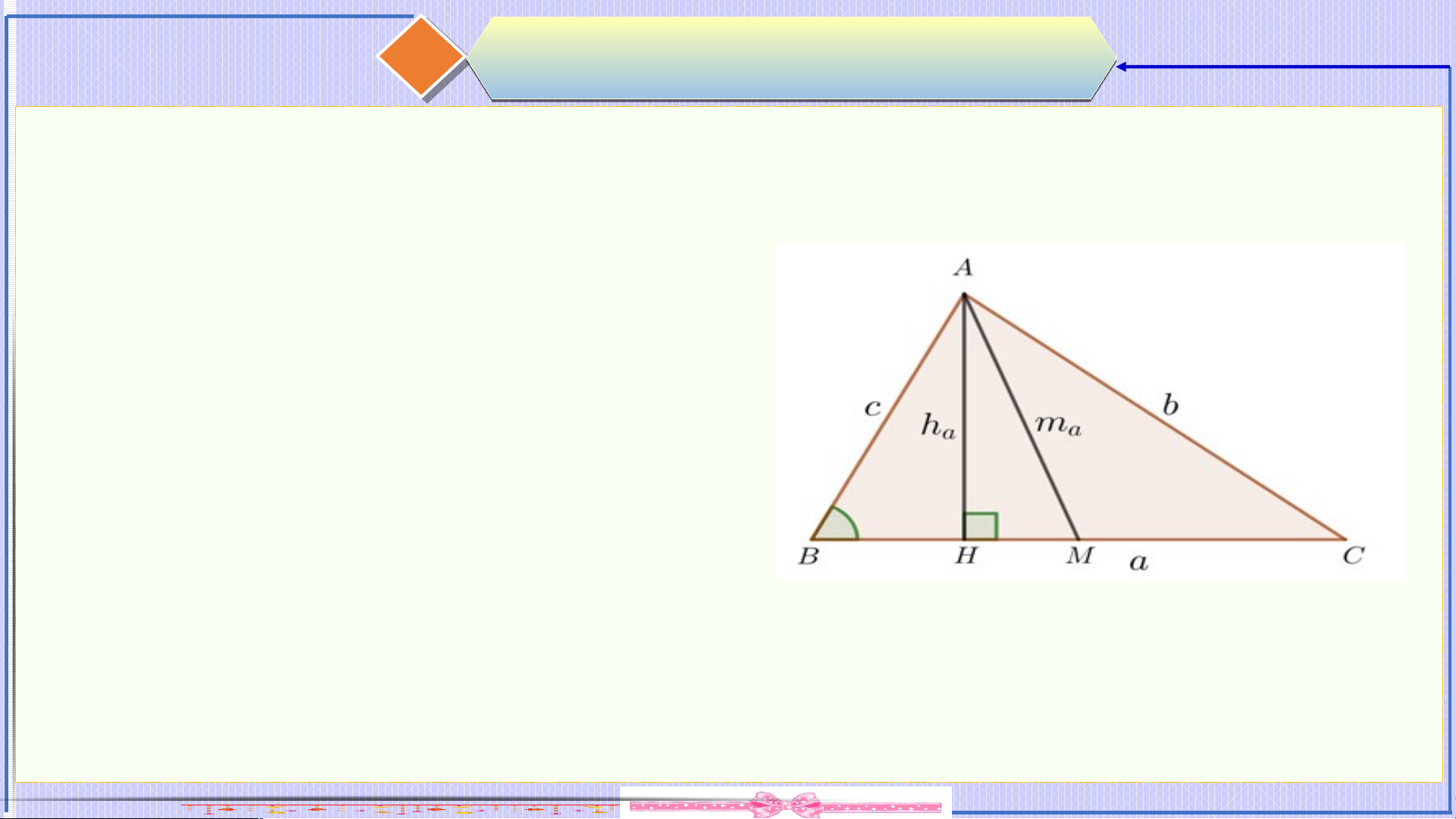
 Cho tam giác có lần lượt là các trung tuyến kẻ từ . Ta có: • • •
. Định lý sin:
 Trong tam giác với và là bán kính đường tròn ngoại tiếp, ta có: ⓵ Tóm T t ắt lý thuy u ết
➌. Công thức tính diện tích tam giác  Cho tam giác có:
 là độ dài đường cao lần lượt tương ứng với các cạnh ;
 là bán kính đường tròn ngoại tiếp tam giác;
 là bán kính đường tròn nội tiếp tam giác;
 là nửa chu vi tam giác;
 là diện tích tam giác. Khi đó ta có: ⓶ Phân dạng bài tập
①. Dạng 1: Xác định các yếu tố trong tam giác -
Giải tam giác.  Phương pháp
 Sử dụng định lý Cosin, đinh lý sin
 Sử dụng công thức tính độ dài đường trung tuyến và
mối liên hệ của các yếu tố trong các công thức tính diện tích tam giác
 Giải tam giác là tính các cạnh các góc của tam giác
dựa trên một số điều kiện cho trước ⓷ Bài tập minh họa ọ
Câu . Cho tam giác ABC có b = 7; c = 5, . Tính độ dài
cạnh và đường cao của tam giác ABC. . Lời giải:  Ta có:  Mặt khác: (Vì ).  Mà: . ⓷ Bài tập minh họa ọ
Câu . Cho tam giác có Tính của tam giác .  Lời giải:
 Áp dụng hệ quả của định lý cosin, ta có : .  Tam giác vuông tại .
 Khi đó, tam giác vuông có: . ⓷ Bài tập minh họa ọ
Câu . Cho tam giác ABC có , b = 7, . Tính ha và R.  Lời giải:
Diện tích tam giác ABC: .
Độ dài đường cao xuất phát từ A của tam giác ABC: . Độ dài cạnh c: .
Bán kính đường tròn ngoại tiếp tam giác ABC: . ⓶ Ph P ân h ân dạn g dạn bài g bài t ập t
②. Dạng 2: Nhận dạng tam giác  Phương pháp
 Sử dụng các hệ thức lượng trong tam giác và tính chất của
các tam giác đặc biệt: Tam giác vuông, tam giác cân, tam giác đều.  Chú ý :
+ Nếu có thì tam giác vuông đỉnh
+ Nếu có thì tam giác cân đỉnh
+ Nếu có thì tam giác đều. ⓷ Bài tập minh họa ọ
Câu . Xác định dạng tam giác , biết rằng: . . Lời giải:
 Theo công thức Hê rông ta có : .  Do đó :
 Vậy tam giác vuông tại . ⓷ Bài tập minh họa ọ
Câu . Cho tam giác thỏa mãn hệ thức .
Chứng minh rằng tam giác là tam giác cân.  Lời giải:  Ta có : .  Từ suy ra: .
 Vậy tam giác là tam giác cân đỉnh . ⓷ Bài tập minh họa ọ
Câu . Chứng minh rằng nếu trong tam giácta có thì là
tam giác đều.(Trong đó: là nửa chu vi, là bán kính
đường tròn ngoại tiếp tam giác ).  Lời giải:  Ta có: .  Ta lại có : . ⓷ Bài tập minh họa ọ
Câu . Chứng minh rằng nếu trong tam giácta có thì là tam giác
đều.(Trong đó: là nửa chu vi, là bán kính đường tròn ngoại tiếp tam giác ).  Lời giải:  Từ
. Vậy tam giác là tam giác đều. ⓶ Ph P ân h ân dạn g dạn bài g bài t ập t
③. Dạng 3: Chứng minh đẳng thức, bất đẳng thức liên
quan đến các yếu tố trong tam giác, tứ giác.  Phương pháp
 Để chứng minh các đẳng thức liên quan đến các yếu tố ta
sử dụng các phép biến đổi để biến vế này thành vế kia,
sử dụng các công thức lượng giác liên quan số đo các góc
phụ nhau, góc bù nhau. Hệ thức lượng giác cơ bản.
 Sử dụng các bất đẳng thức cơ bản, bất đẳng thức cô - si, bunhiacopsky. ⓷ Bài tập minh họa ọ
Câu . Chứng minh rằng trong tam giác , nếu thì  Lời giải:  Ta có: . ⓷ Bài tập minh họa ọ
Câu . Tam giác vuông cân tại và nội tiếp trong đường
tròn tâm bán kính . Gọi là bán kính đường tròn
nội tiếp tam giác . Chứng minh rằng .  Lời giải:  Ta có: ,
 Vì tam giác vuông cân tại nên và  Ta có : .(đpcm) ⓷ Bài tập minh họa ọ
Câu . Cho tam giác có các cạnh thỏa mãn hệ thức . Chứng minh rằng .  Lời giải:  Ta có .  Mà . ⓶ Ph P ân h ân dạn g dạn bài g bài t ập t
④. Dạng 4: Bài toán thực tế về đo đạc khoảng cách.  Phương pháp
 Vận dụng các công thức hệ thức lượng trong tam giác
vào thực tế đo đạc tính khoảng cách, chiều cao của một
số đối tượng mà không cần đo trực tiếp. ⓷ Bài tập minh họa ọ
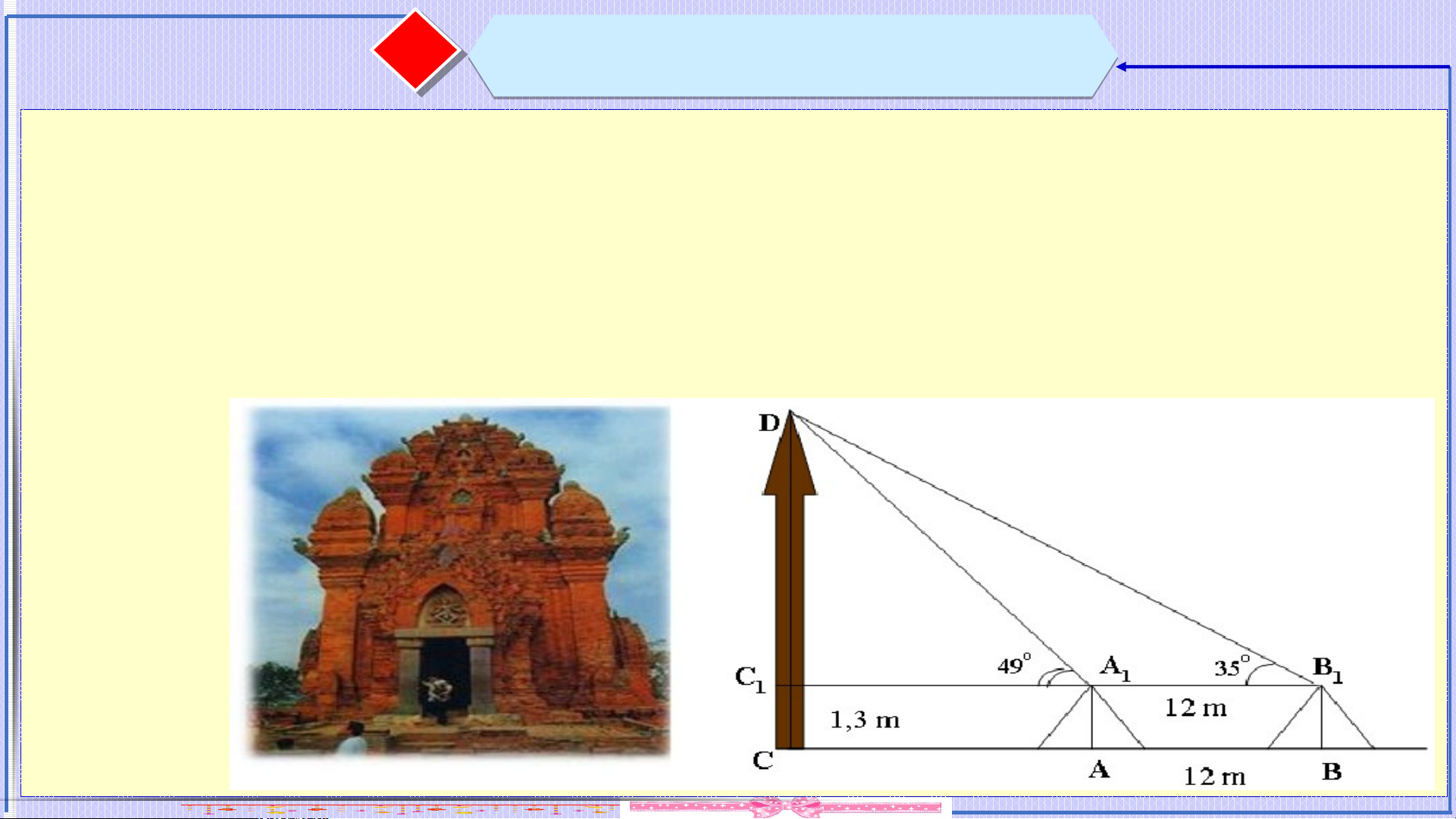
Câu . Muốn đo chiều cao của tháp chàm Por Klong Garai ở Ninh
Thuận người ta lấy hai điểm và trên mặt đất có khoảng
cách cùng thẳng hàng với chân của tháp để đặt hai giác
kế. Chân của giác kế có chiều cao . Gọi là đỉnh tháp và hai
điểm , cùng thẳng hàng với thuộc chiều cao của tháp.
Người ta đo được góc và . Tính chiều cao của tháp. ⓷ Bài tập minh họa ọ
Câu . Muốn đo chiều cao của tháp chàm Por Klong Garai ở Ninh Thuận
người ta lấy hai điểm và trên mặt đất có khoảng cách cùng
thẳng hàng với chân của tháp để đặt hai giác kế. Chân của giác
kế có chiều cao . Gọi là đỉnh tháp và hai điểm , cùng thẳng hàng
với thuộc chiều cao của tháp. Người ta đo được góc và . Tính chiều cao của tháp.  Lời giải:  Ta có ; , nên .  Xét tam giác , có .
 Xét tam giác vuông tại , có: . ⓷ Bài tập minh họa ọ
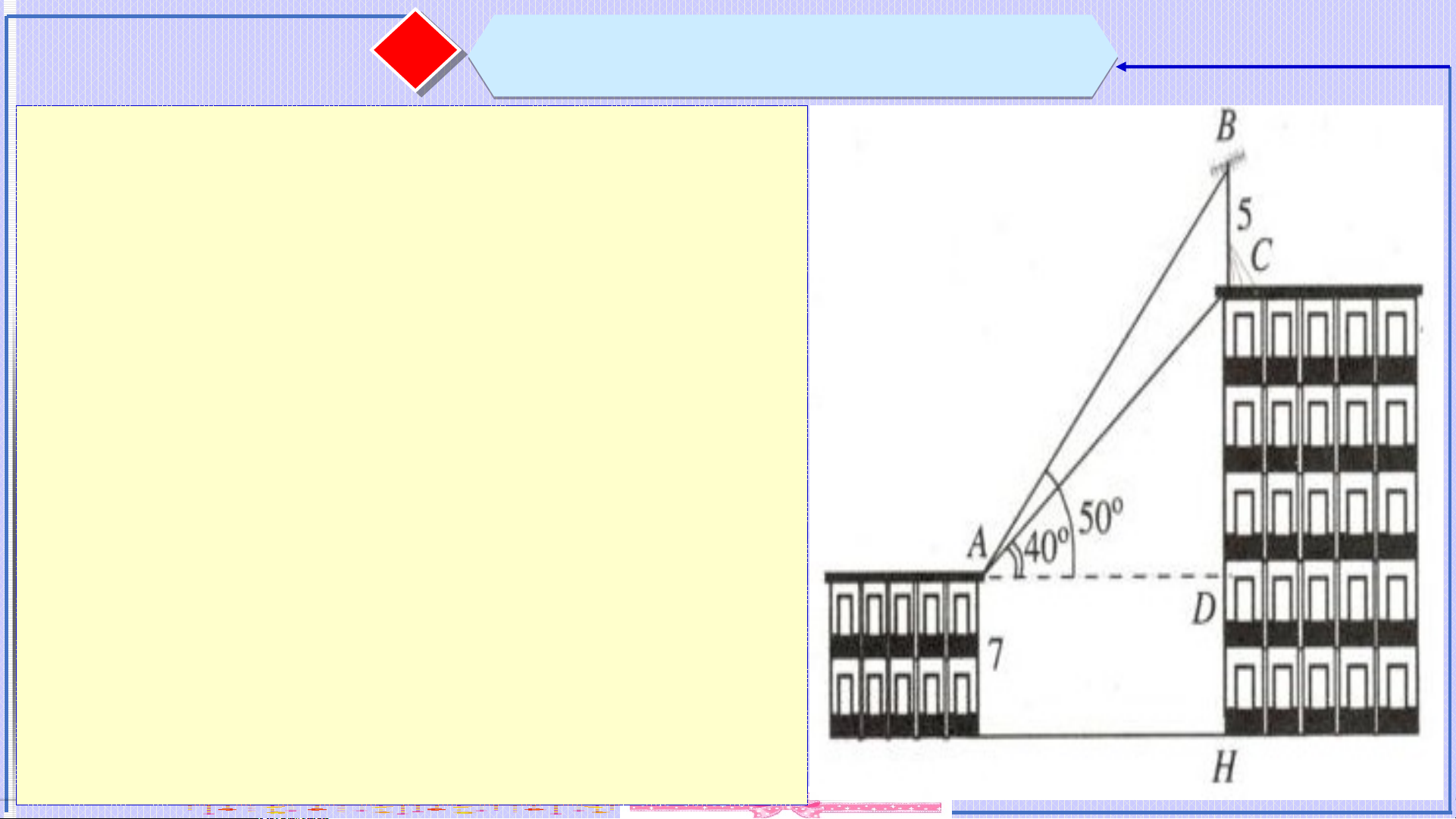
Câu . Trên nóc một tòa nhà có cột ăng-ten cao . Từ vị trí quan sát cao so
với mặt đất, có thể nhìn
thấy đỉnh và chân của cột ăng-ten dưới góc và so với phương nằm ngang (như hình vẽ bên). Tính chiều cao
của tòa nhà (được làm tròn đến hàng phần mười). ⓷ Bài tập minh họa ọ  Lời giải:
 Ta có chiều cao của tòa nhà chính là đoạn .  Mà .
 Xét tam giác vuông tại có
 Xét tam giác vuông tại có  Xét tam giác có: (m).  Vậy tòa nhà cao . ⓷ Bài tập minh họa ọ
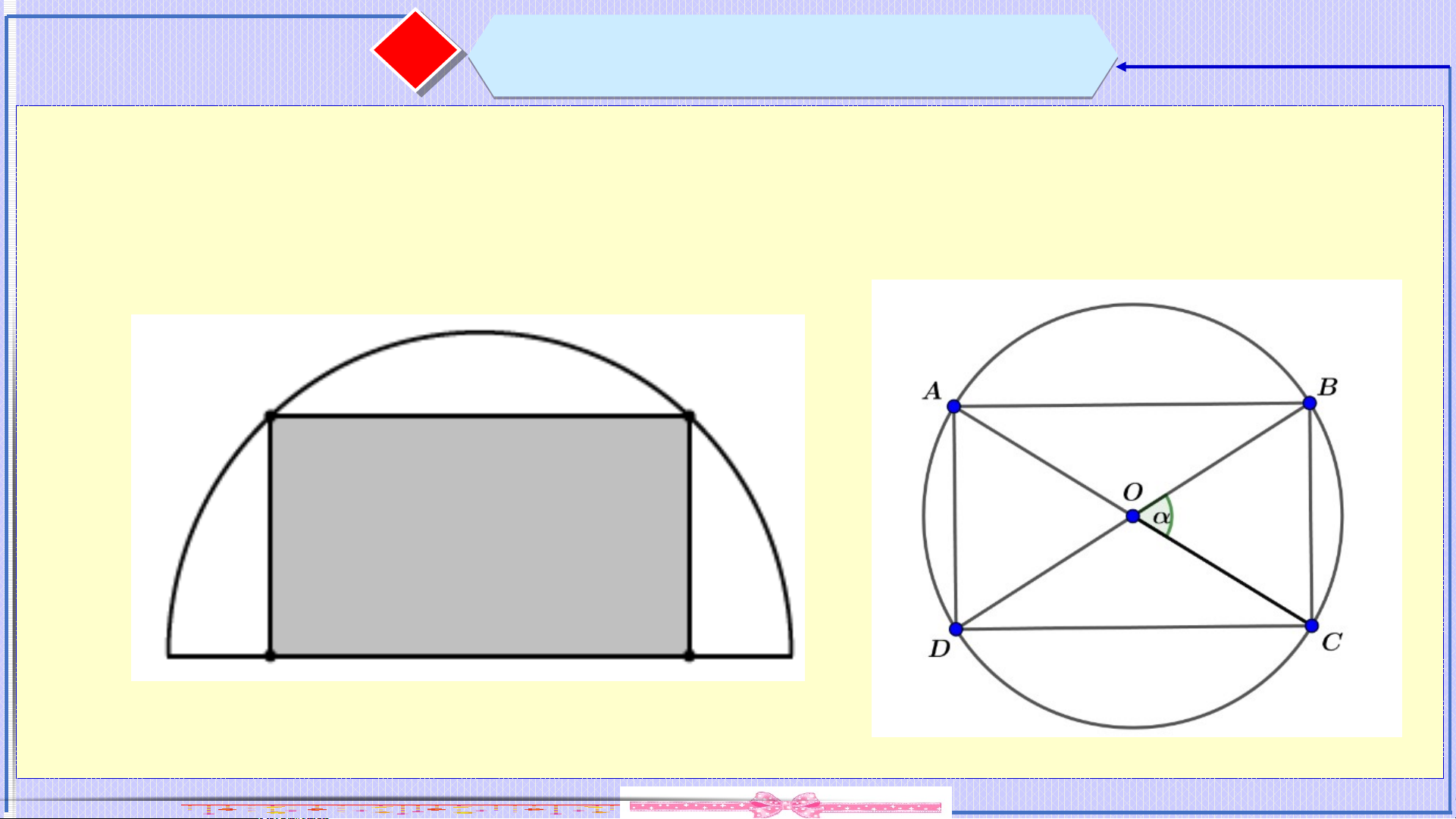
Câu . Từ một miếng tôn có hình dạng là nửa đường tròn
bán kính , người ta cắt ra một hình chữ nhật. Hỏi
có thể cắt được miếng tôn có diện tích lớn nhất là bao nhiêu? ⓷ Bài tập minh họa ọ
Câu . Từ một miếng tôn có hình dạng là nửa đường tròn bán
kính , người ta cắt ra một hình chữ nhật. Hỏi có thể cắt
được miếng tôn có diện tích lớn nhất là bao nhiêu?  Lời giải:
 Xét đường tròn bán kính , ta cắt trên đó một hình chữ nhật .  Khi đó .
 Dấu bằng xảy ra khi và chỉ khi .
 Vậy diện tích lớn nhất của miếng tôn cắt trên nửa đường tròn bằng .
Document Outline

• Slide 1
• Slide 2
• Slide 3
• Slide 4
• Slide 5
• Slide 6
• Slide 7
• Slide 8
• Slide 9
• Slide 10
• Slide 11
• Slide 12
• Slide 13
• Slide 14
• Slide 15
• Slide 16
• Slide 17
• Slide 18
• Slide 19
• Slide 20
• Slide 21
• Slide 22
• Slide 23
• Slide 24
• Slide 25