Giáo án điện tử Toán 11 Bài 1 Chân trời sáng tạo: Phép tính lũy thừa
Bài giảng PowerPoint Toán 11 Bài 1 Chân trời sáng tạo: Phép tính lũy thừa hay nhất, với thiết kế hiện đại, dễ dàng chỉnh sửa giúp Giáo viên có thêm tài liệu tham khảo để soạn Giáo án Toán 11. Mời bạn đọc đón xem!
Chủ đề: Bài giảng điện tử Toán 11
Môn: Toán 11
Sách: Chân trời sáng tạo
Thông tin:
Tác giả:
Preview text:
THÂN MẾN CHÀO ĐÓN CẢ LỚP ĐẾN VỚI TIẾT HỌC HÔM NAY! KHỞI ĐỘNG
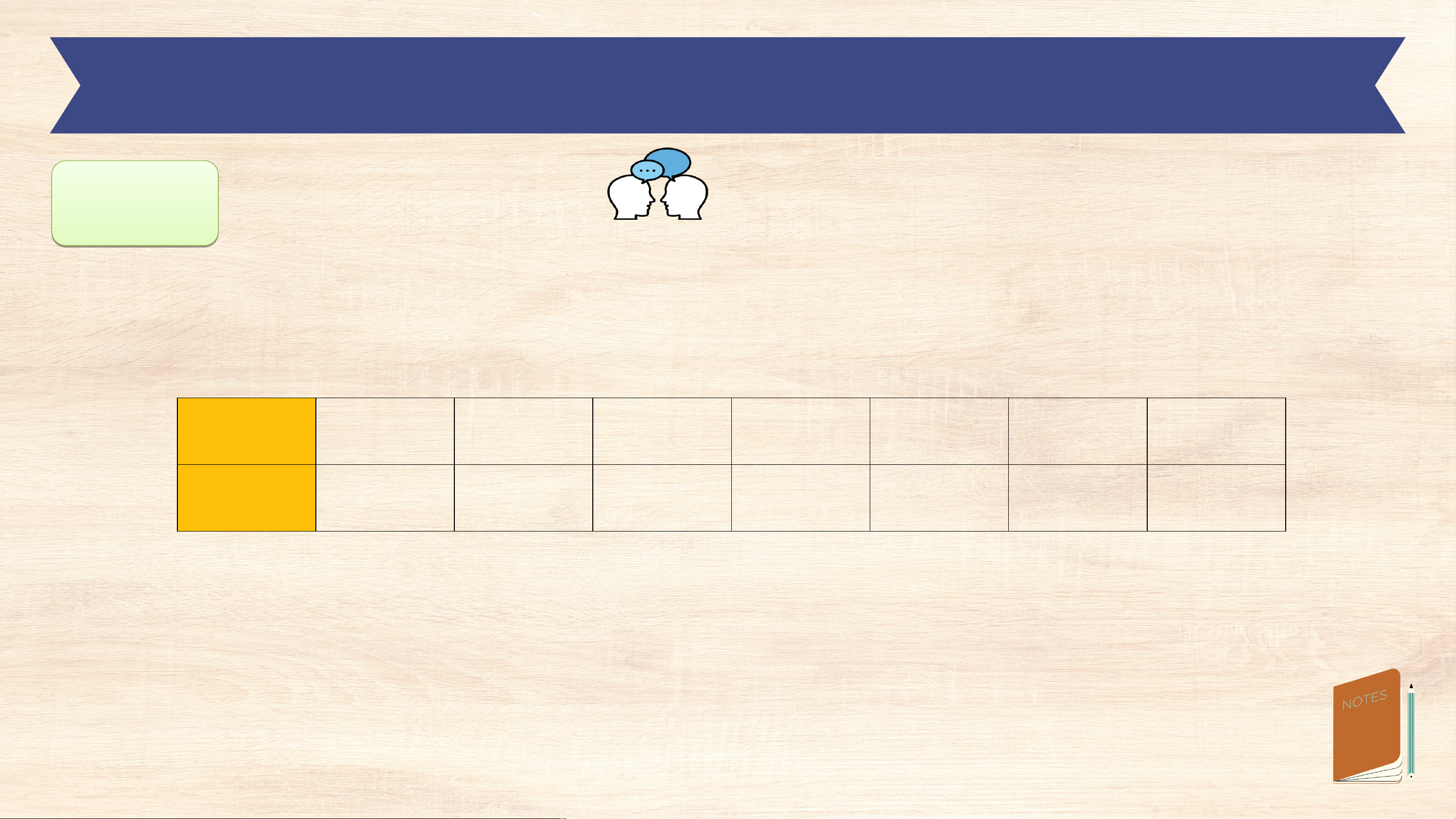
Trong khoa học, người ta thường dùng lũy thừa để ghi các số, có thể rất lớn
hoặc rất bé. Chẳng hạn, bảng dưới đây cho một số ví dụ về cách ghi độ dài Độ dài (m) Ghi bằng luỹ thừa (m) Ghi bằng đơn vị KHỞI ĐỘNG Độ dài (m) Ghi bằng luỹ thừa (m) Ghi bằng đơn vị
Cách ghi như vậy có tiện ích gì? Từ các lũy thừa quen thuộc ở ba dòng đầu, hãy
dự đoán quy tắc viết lũy thừa ở ba dòng cuối KHỞI ĐỘNG KẾT QUẢ
Cách ghi bằng lũy thừa giúp cho việc viết và đọc số (đặc biết với
các số rất lớn hoặc rất bé) ngắn gọn. Nhận thấy Tương tự:
Từ đó dự đoán (nghịch đảo của với n là số tự nhiên khác 0.
CHƯƠNG VI: HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
BÀI 1. PHÉP TÍNH LŨY THỪA NỘI DUNG BÀI HỌC 01
Lũy thừa với số mũ nguyên 02 Căn bậc 03
Lũy thừa với số mũ hữu tỉ 04
Lũy thừa với số mũ thực 05
Tính chất của phép tính lũy thừa
1. LŨY THỪA VỚI SỐ MŨ NGUYÊN HĐ H K Đ P K 1 P
Thảo luận nhóm đôi, hoàn thành HĐKP1.
Cho biết dãy số được xác định theo một quy luật nào đó và bốn số
hạng đầu tiên của nó được cho như ở bảng dưới đây
a) Tìm quy luật của dãy số và tìm ba số hạng tiếp theo của nó
b) Nếu viết các số hạng của dãy số dưới dạng lũy thừa, thì bốn số
hạng đầu tiên có thể viết thành . Dự đoán cách viết dưới dạng lũy thừa
của ba số hạng tiếp theo của dãy số và giải thích
1. LŨY THỪA VỚI SỐ MŨ NGUYÊN Giải b) Ta có
a) Quy luật: mỗi số hạng (kể từ số
hạng thứ hai) bằng một nửa số hạng . kề trước
Ta thấy, các số hạng này của ,
dãy đều viết được dưới dạng luỹ
thừa của 2 với số mũ giảm dần: Từ đó
. Từ đó, dự đoán rằng các số
hạng tiếp theo lần lượt là .
Với số nguyên dương , số thực , luỹ KẾT LUẬN
thừa của với số mũ xác định bởi Chú ý: a) với mọi
b) và ( với không có nghĩa. Ví V dụ d 1
Tính giá trị các biểu thức sau: 1 1 ¿ = a) 1 1 16 − 242 16 ¿9. =9. =9. 9. 2 9 9 =16 b) (34) (3 −2 4 )1 16 1 ¿ :1= =4 :(√3)0 2 1 c) (12) (12) 4 Thực c h àn à h 1
Tính giá trị các biểu thức sau: 1 1 1 −5 1 1 ¿1. =1. = =32 5 ¿ 20. 1 1 a) b) −5=− 5 (12) (12) 25 32 −3 1 1 1 1 1 1 1 1 1 1 ¿ . : = . : . : .27.4=3 6−2.
:2−2 62 3 22 36 1 4=36 1 4=36 c) (13) (13) 33 27 VẬN DỤNG 1
Trong khoa học, người ta thường phải ghi các số rất lớn hoặc rất bé. Để
tránh phải viết và đếm quá nhiều chữ số 0, người ta quy ước cách ghi các
số dưới dạng , trong đó và là số nguyên
Khi một số được ghi dưới dạng này, ta nói nó được ghi dưới dạng kí hiệu khoa học.
Chẳng hạn, khoảng cách km từ Trái Đất đến Mặt Trời được ghi dưới dạng kí hiệu khoa học là km.
a) Vận tốc ánh sáng trong chân không là m/s
b) Khối lượng nguyên tử của oxygen là kg Giải a) ; b) . 2. CĂN BẬC HĐ H K Đ P K 2
PMột thùng gỗ hình lập phương có độ dài cạnh ().
Kí hiệu và lần lượt là diện tích một mặt và thể tích của thùng gỗ này. a) Tính và khi và khi b) bằng bao nhiêu để ? c) bằng bao nhiêu để ? Giải a) Khi thì . Khi thì . 2. CĂN BẬC HĐ H K Đ P K 2
PMột thùng gỗ hình lập phương có độ dài cạnh ().
Kí hiệu và lần lượt là diện tích một mặt và thể tích của thùng gỗ này. a) Tính và khi và khi b) bằng bao nhiêu để ? c) bằng bao nhiêu để ? Giải b) . c) . KẾT LUẬN
Cho số nguyên dương và số thực bất
kì. Nếu có số thực sao cho
Thì được gọi là căn bậc của b.
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15