








Preview text:
HOẠT ĐỘNG KHỞI ĐỘNG Kh K i h xây y tườ ư ng gạ n ch, người thợ thường hư bắt đầu với vi v ệc ệ xây các v iên n gạ g ch dẫn, sau đó că
u đó c ng dây nhợ dọc theo cạnh củ nh c a a các viên gạc
n gạ h dẫn đó để làm chuẩn rồi mới xây các á viên gạch tiếp theo. H1. Vi V ệc c sử dụ d n ụ g dây d căng ăn nh n ư h vậy có vậy c t ác dụ d n ụ g g gì g ? H2. Toá T n n học
h mô tả vị trí giữa dây d căng, ăn các mép p gạch h với mặt đất n đ h ất n ư thế ư th nào? n Bµi 12.
ĐƯỜNG THẲNG VÀ MẶT PHẲNG SONG SONG HOẠT ĐỘNG Hã H y quan sá n s t hình n ả nh khung thành bóng đá và và
nhận xét vị trí của xà ủa ngan nga g, g c ột d ọc, t ọc hanh chống và c thanh bên của khung thành với mặt đấ đ t. GỢI Ý VẤN ĐỀ Hã H y qua ã n sát hình vẽ và * B’C’ * B’C’ và v xá x m c đị p(A nh B số gi CD) CD k ao đ hôn h i ao đgể m ểc ó điểm chung c của ủa c ác đường thẳng B’ B B’C’ C ’ Cs , A , on A’ AA g s , oA , n B, Ag v vớià v m m ặ p( t ABCD) phẳn phẳ g g (AB (A CD B )? CD Trong không T * A * A’ AA ’và v mp(ABCD A ) c
BCD ó một điểm chun hu g gian có bao nhiêu vị trí có AA’ cắt mp(ABCD) thể xảy ra giữa ữa đường thẳng d * A * B và A mp(ABC p(A D BC ) D c ó vô số đi ố ểm chung và mp(P) (P ? ? AB nằm trong mp(ABCD)
BÀI 12. ĐƯỜNG THẲNG VÀ MẶT PHẲNG SONG SONG I. I ĐƯ Đ ỜNG N G T H T Ẳ H NG S N ON G S G S ON O G S NG O NG V ỚI V M ỚI ẶT Ặ P T H P ẲNG Ẳ
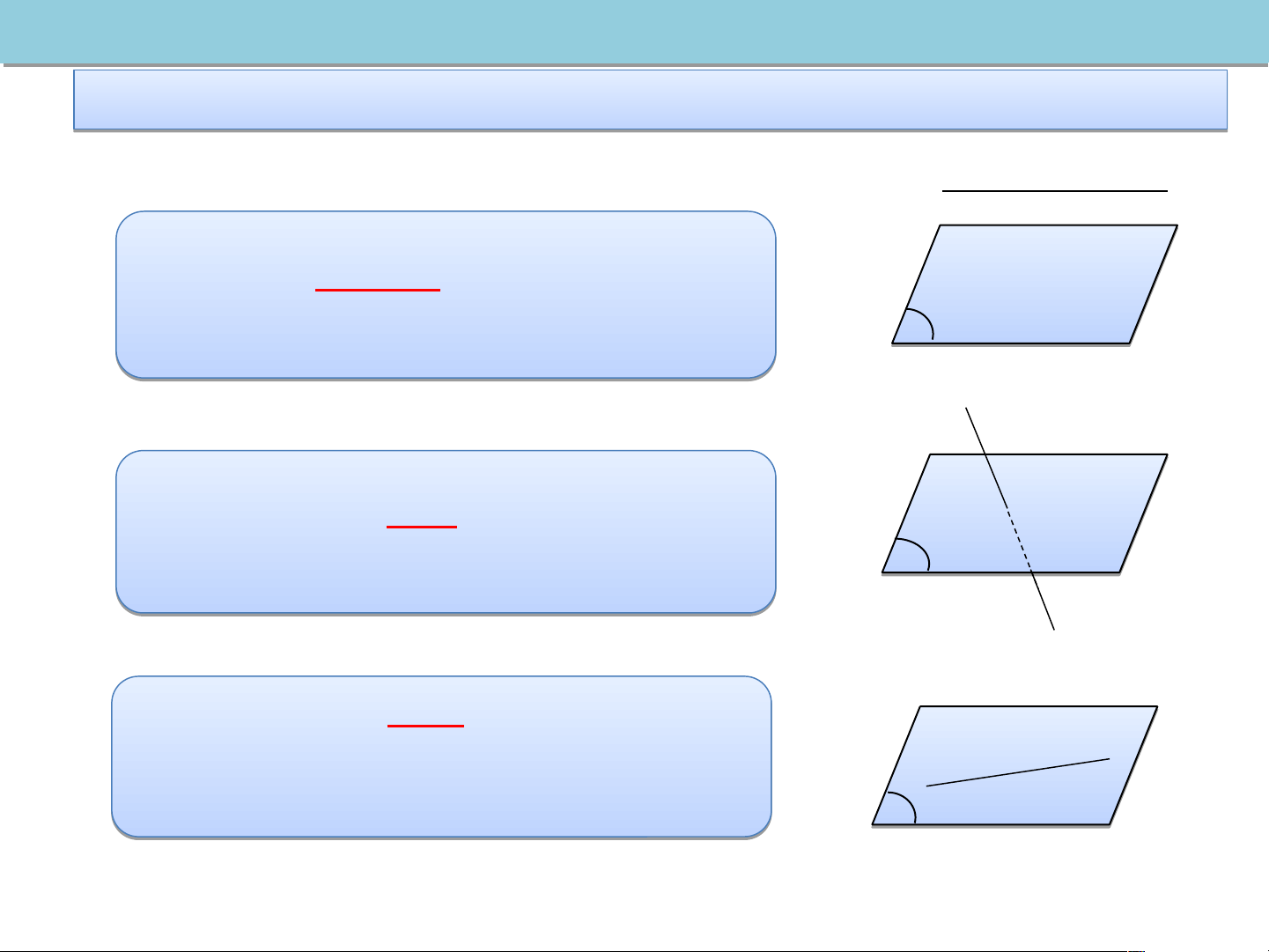
Cho đường thẳng d và mặt phẳng (P) d • d và (P) P khôn h g ôn có đi đ ểm ể chung. Ta T nói: d d và v (P) P song on s ong với nha n u. P d // (P) d
• d và (P) có một điểm chung duy M
d và (P) có một điểm chung duy nh n ất ấ . T a T nói: d d và v (P) ) cắt nhau P d (P)= M • d và (P) P ) có
ó từ 2 điểm chung trở lên. Ta T nói ó : d nằm trong on (P) P hay A B (P) c P hứa d hứa P d (P)
Định nghĩa: Đường thẳng song song với mặt phẳng nếu
chúng không có điểm chung. Nê
N u định nghĩa đường thẳng so s ng ng song với s mặt phẳng n ? Qua Q n s n á
s t phòng học và lấy ví
dụ về vị trí tương đối giữa ữ
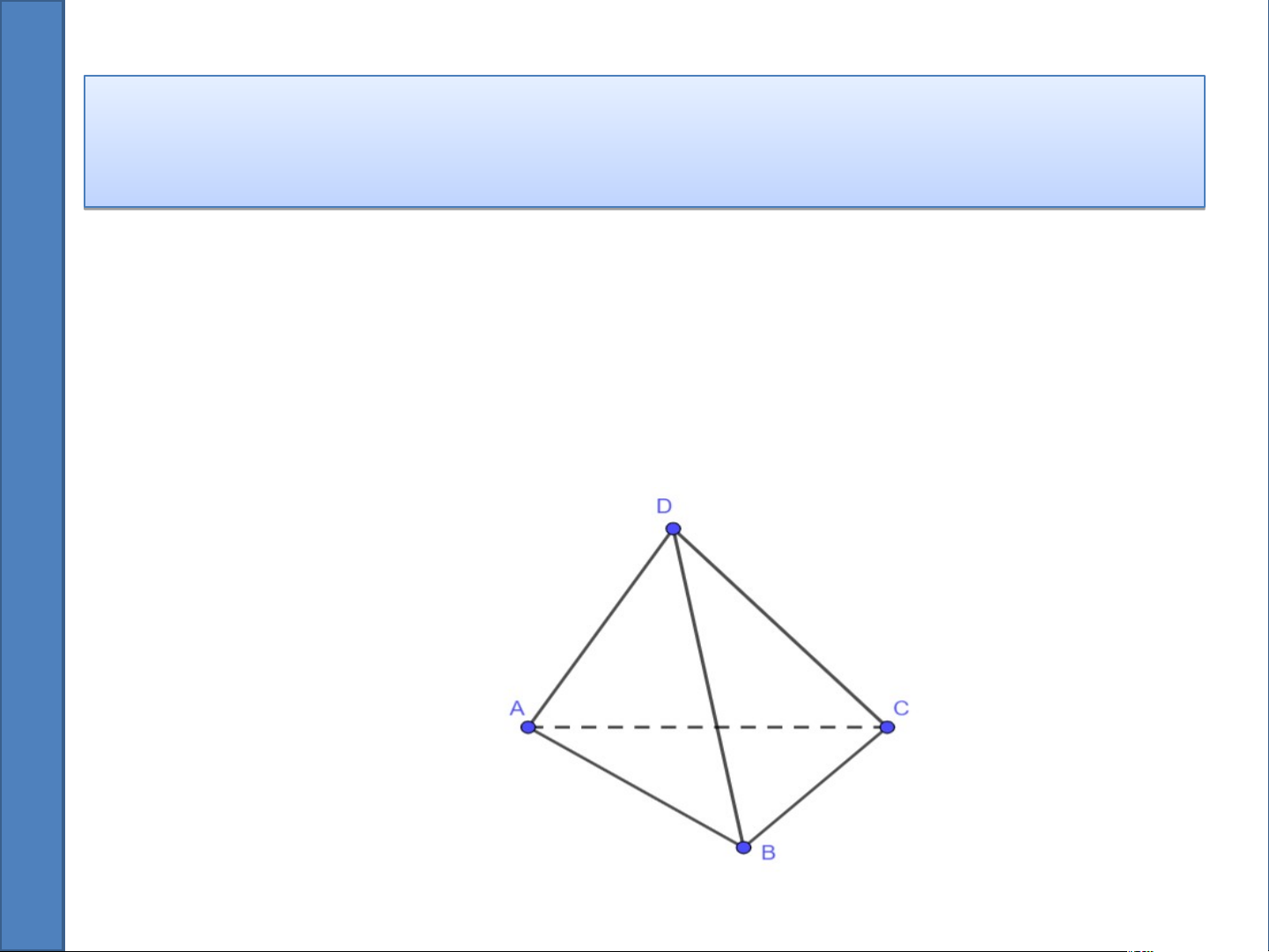
đường thẳng và mặt phẳng trong không gian? Ví V dụ 1 dụ . C . ho hì C nh t nh ứ di ứ d ện A ện B A C B D C . D T . r T ong các r m ong các ặt m phẳng chứa ng c các m ặ các m t c t ủ c a h a ình n t ứ di ứ ện, hãy ện, cho c bi ết: ết
a. Đường thẳng AB cắt các mặt phẳng nào ?
b. Đường thẳng AB nằm trong mặt phẳng nào ? GỢI Ý VẤN ĐỀ
II. ĐIỀU KIỆN VÀ TÍNH CHẤT CỦA ĐƯỜNG THẲNG SONG
SONG VỚI MẶT PHẲNGNhận xét gì về vị trí tương đối của d và ? d /
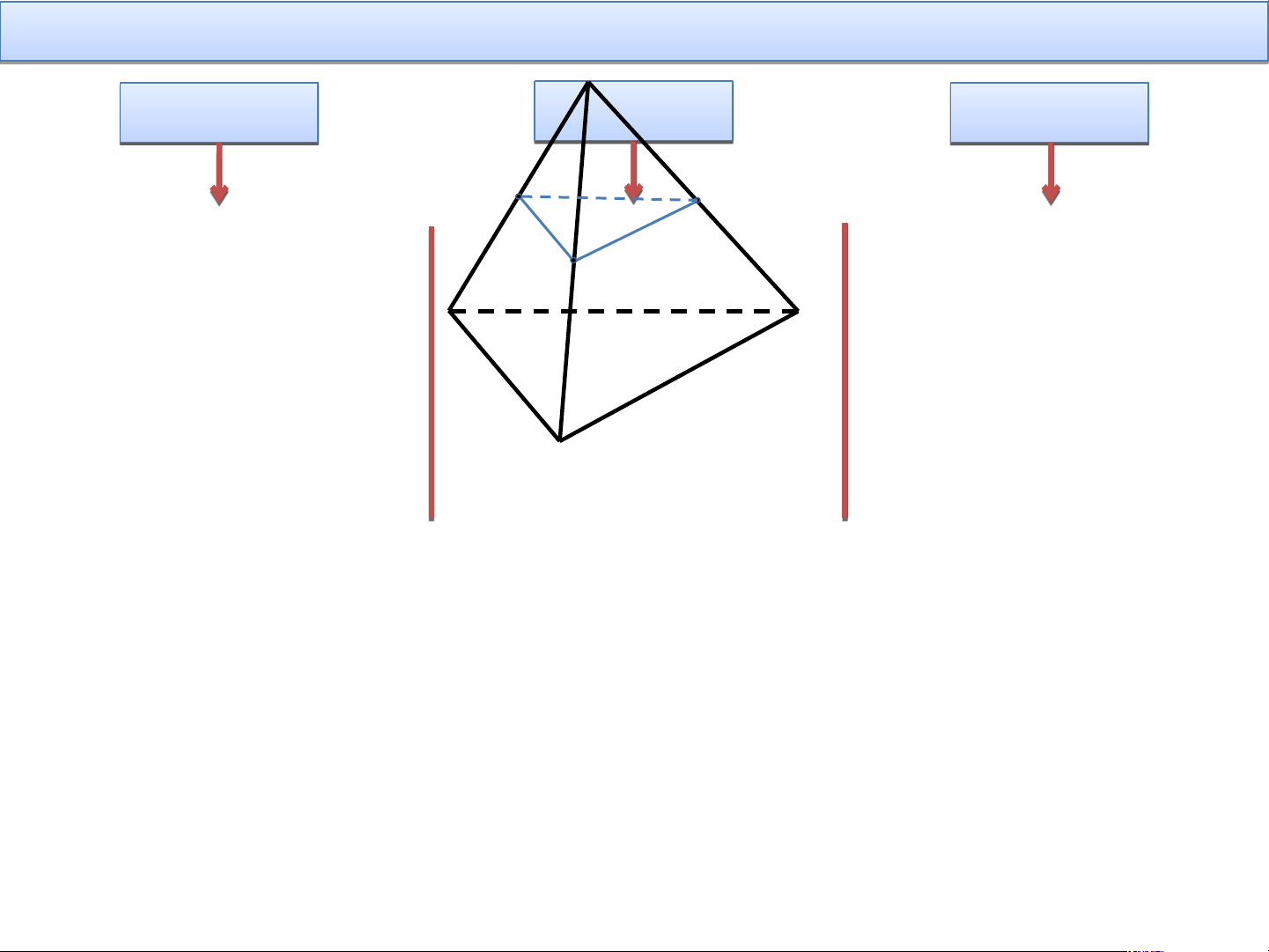
Cho d d / / / d / /d d d’ ) B.P Các C h h chứn h g ứn minh n đườ đ ng n thẳn h g ẳn son o g song on với mặt ph p ẳng ẳn Để Để ch c ứng ứn min m h h đườn ườ g n th t ẳ h ng n son s g so s ng n với vớ một m mặ m t t phẳn h g ta t ch c ứn h g min m h h đư đ ờn ờ g n th t ẳn h g đó kh k ông ôn nằm n ằm tr t o r ng n mặ m t tphẳn h g và so s ng n son s g với ớ mộ m t tđườ đ n ườ g th t ẳng ẳn thu h ộ u c c mặ m t t phẳn h g ấy. y Ví V dụ d ụ 1: Cho C tứ diện ABCD A . BCD Gọi ọ M, M N, N P P lần lượt là trung điểm của c AB A , B AC, A AD A . D Chứng C
minh các đường thẳng MN, N NP N , P P M s M ong song v ong s ớ ong v i mặt phẳng (BCD (B )? CD BẢ B NG Ả NG PH P ÂN H CÔ ÂN N CÔ G NH N I G NH Ệ I M M VỤ VỤ CÁ C C N Á HÓ C N M HÓ A NHÓ NH M HÓ ÓM 1 1 NHÓ N NH M HÓ ÓM M 2 2 NH N Ó NH HÓM Ó 3 M P * * C Chứng ng minh: h: MN MN / // (BCD) * C * Chứng m g minh nh: N NP P / // ( (BCD) * C * Chứng m g minh nh: P PM // ( (BCD) B N D C
TÓM TẮT NỘI DUNG BÀI HỌC Đt song song mp
I. VỊ TRÍ TƯƠNG ĐỐI GIỮA Đt cắt mp
ĐƯỜNG THẲNG VÀ MẶT PHẲNG Đt nằm trong mp
II. ĐIỀU KIỆN ĐƯỜNG THẲNG SONG SONG VỚI MẶT PHẲNG d /
Cho d d / / / d / /d
Phương pháp chứng minh đường
thẳng song song với mặt phẳng. BÀI TẬ TẬP CỦNG CỐ
Câu 1. Trong không gian có bao nhiêu vị trí tương đối giữa
đường thẳng và mặt phẳng? A. 1 B. 2 C. 3 D. 4
Câu 2. Cho hình chóp S.ABCD, đáy ABCD là hình bình hành.
Gọi M, N lần lượt là trung điểm của cạnh SA, SB. Khi đó:
A. MN song song với mặt phẳng (ABCD).
B. MN song song với mặt phẳng (SAB).
C. MN song song với mặt phẳng (SCD). D. Cả A và C. BÀI TẬ TẬP CỦNG CỐ
Câu 3. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Cho đường thẳng a song song với mp(P) và đường thẳng b
bất kì nằm trong (P) thì a song song với b.
B. Hai đường thẳng phân biệt cùng song song với một mặt
phẳng thì chúng song song với nhau.
C. Cho đường thẳng a không nằm trên mp(P). Nếu đường
thẳng a song song với đường thẳng b nằm trong mặt phẳng (P)
thì đường thẳng a song song với mp (P)
D. Cả 3 mệnh đề trên đều sai? BÀI TẬP CỦNG CỐ
Câu 4: Cho hai đường thẳng a, b phân biệt và mặt phẳng (P).
Giả sử a song song với b và b song song với (P). Hãy chọn kết quả đúng: a) a song song với (P) b) a nằm trên (P)
c) a song song với (P) hoặc a nằm trong (P)
d) Không xác định được vị trí của a với (P) 15 Bài tập trắc nghiệm
Câu 5 : Cho mặt phẳng (P) và đường thẳng a song song với
(P). Giả sử b là một đường thẳng nằm trong (P). Hãy chọn mệnh đề đúng: a) a song song b b) a và b chéo nhau
c) a và b không có điểm chung d) a và b đồng phẳng 16
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- BÀI TẬP CỦNG CỐ
- Bài tập trắc nghiệm




