


















Preview text:
CHÀO MỪNG TẤT CẢ CÁC EM
ĐẾN VỚI BÀI HỌC HÔM NAY! KHỞI ĐỘNG Nghịch lý Zeno
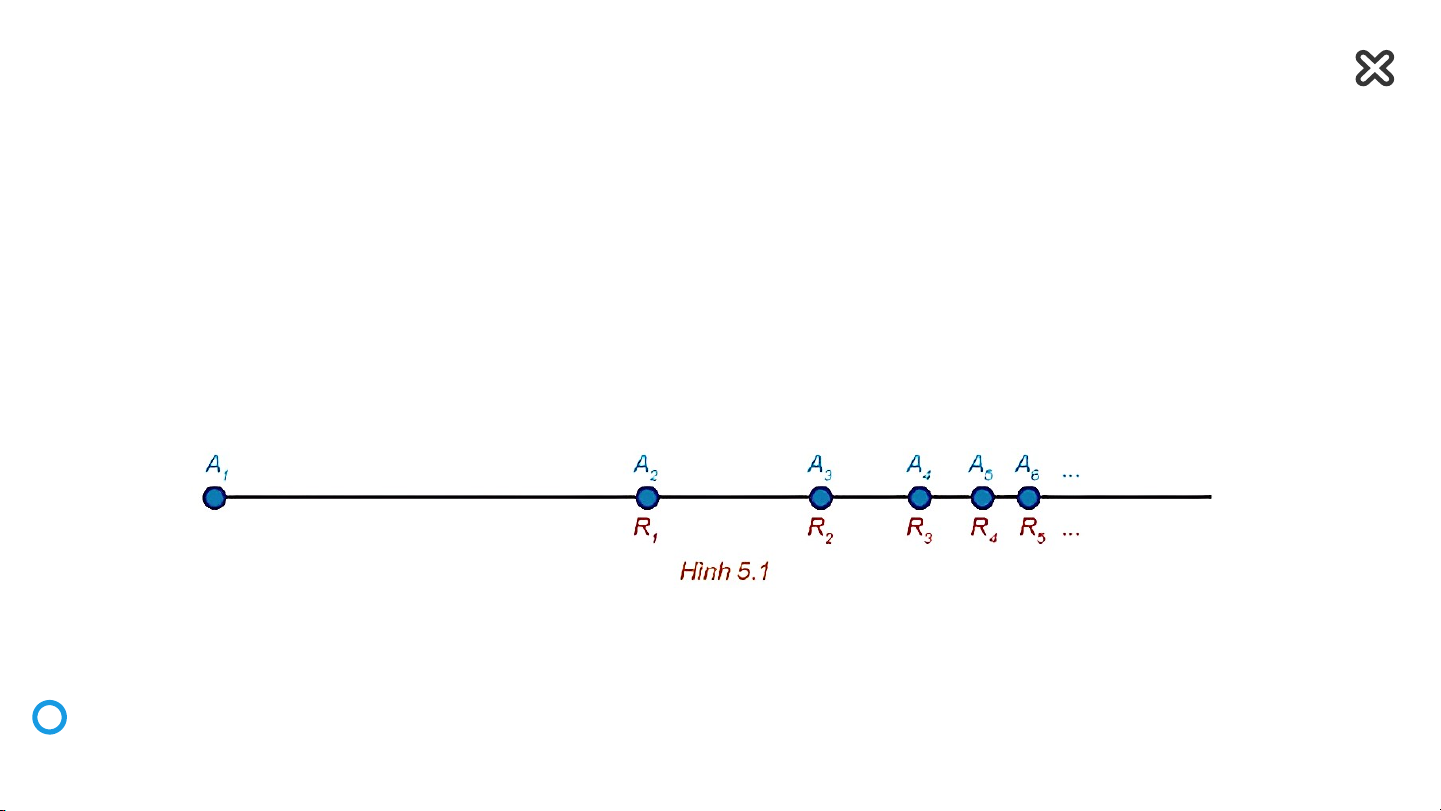
Achil es (nhân vật trong thần thoại Hy Lạp, được mô tả có thể chạy nhanh như gió)
đuổi theo một con rùa trên một đường thẳng. Vị trí xuất phát của Achil es là , cách
vị trí xuất phát của rùa một quãng đường có chiều dài là a. Zeno lí luận rằng, mặc dù
chạy nhanh hơn nhưng Achil es không bao giờ đuổi kịp rùa.
Thật vậy, trước tiên Achil es phải đến được vị trí trong khoảng thời gian này, rùa đã di
chuyển đến vị trí . Sau đó, Achilles phải đến được vị trí , lúc này rùa đã di chuyển đến
vị trí Cứ như vậy, Achilles không bao giờ đuổi kịp rùa.
CHƯƠNG V. GIỚI HẠN. HÀM SỐ LIÊN TỤC
BÀI 15: GIỚI HẠN CỦA DÃY SỐ
CREDITS: This presentation template was created
by Slidesgo, and includes icons by Flaticon and
infographics & images by Freepik and content by Swetha Tandri NỘI DUNG BÀI HỌC 01
Giới hạn của dãy số 02
Định lí về giới hạn hữu hạn của dãy số 03
Tổng của cấp số nhân lùi vô hạn 04
Giới hạn vô cực của dãy số 01 GIỚI HẠN CỦA DÃY SỐ HĐ1
Nhận biết dãy số có giới hạn là 0 Cho dãy số với
a) Biểu diễn năm số hạng đầu của dãy số này trên trục số.
b) Bắt đầu từ số hạng nào của dãy, khoảng cách từ đến 0 nhỏ hơn 0,01? Trả lời:
a) Năm số hạng đầu của dãy số đã cho là .
Biểu diễn các số hạng này trên trục số, ta được: 𝑢 𝑢 𝑢 𝑢 𝑢 1 3 5 4 2 −1 0 1 HĐ1
Nhận biết dãy số có giới hạn là 0 Cho dãy số với
a) Biểu diễn năm số hạng đầu của dãy số này trên trục số.
b) Bắt đầu từ số hạng nào của dãy, khoảng cách từ đến 0 nhỏ hơn 0,01? Trả lời:
b) Khoảng cách từ đến 0 là . Ta có:
Vậy bắt đầu từ số hạng thứ 101 của dãy thì khoảng cách từ đến 0 nhỏ hơn 0,01. KHÁI NIỆM
Ta nói dãy số có giới hạn là 0 khi n dần tới dương vô
cực, nếu có thể nhỏ hơn một số dương bé tùy ý, kể từ
một số hạng nào đó trở đi, kí hiệu hay khi . Ví dụ 1:
Xét dãy số với . Giải thích vì sao dãy số này có giới hạn là 0. Giải
Dãy số này có giới hạn là 0, bởi vì có thể nhỏ hơn một số dương bé tuỳ ý khi đủ lớn.
Chẳng hạn, để tức là , ta cần hay .
Như vậy các số hạng của dãy kể từ số hạng thứ 101 đều có giá trị tuyệt đối nhỏ hơn . Chú ý
Từ định nghĩa dãy số có giới hạn 0, ta có kết quả như sau:
với k là một số nguyên dương. nếu
Nếu với mọi và thì . LU LYUỆYNỆ T N Ậ TPẬ 1 P 1 Giả i i Xét dãy số có Chứng minh rằng Ta có: ; Do đó, . HĐ2
Nhận biết dãy số có giới hạn hữu hạn
Cho dãy số với . Xét dãy số xác định bởi . Tính Trả lời: Ta có: Do đó ĐỊNH NGHĨA
Ta nói dãy số có giới hạn là số thực a khi n dần tới
dương vô cực nếu , kí hiệu hay khi .
Xét dãy số với Chứng minh rằng. Ví dụ 2: Giải Ta có khi Do vậy . Chú ý khi và chỉ khi
Nếu (c là hằng số) thì LU LYUỆYNỆ T N Ậ TPẬ 2 P 2
Cho dãy số với . Chứng minh rằng Giải Ta có: khi Do vậy . VẬ V N Ậ N DỤ D N Ụ G N 1
Một quả bóng cao su được thả từ độ cao 5 m xuống mặt sàn. Sau mỗi lần
chạm sàn, quả bóng nảy lên độ cao bằng độ cao trước đó. Giả sử rằng quả
bóng luôn chuyển động vuông góc với mặt sàn và quá trình này tiếp diễn vô
hạn lần. Giả sử là độ cao (tính bằng mét) của quả bóng sau lần nảy lên
thứ . Chứng minh rằng dãy số có giới hạn là 0. LUYỆN TẬP 50:50
Câu 1. Dãy số nào sau đây có giới hạn 0? A. C. B. D .
Bài tập 5.4 (SGK-tr109)
Viết các số thập phân vô hạn tuần hoàn sau đây dưới dạng phân số: a) 1,(12) = 1,121212...; b) 3,(102) = 3,102102102... Giải ả b) Ta có:
Do là tổng của cấp số nhân lùi vô hạn với và nên: Vậy VẬN DỤNG
Bài tập 5.5 (SGK-tr109)
Một bệnh nhân hằng ngày phải uống một viên thuốc 150 mg. Sau ngày
đầu, trước mỗi lần uống, hàm lượng thuốc cũ trong cơ thể vẫn còn 5%.
Tính lượng thuốc có trong cơ thể sau khi uống viên thuốc của ngày thứ 5.
Ước tính lượng thuốc trong cơ thể bệnh nhân nếu bệnh nhân sử dụng
thuốc trong một thời gian dài.
Document Outline
- Slide 1
- KHỞI ĐỘNG
- Slide 3
- 04
- GIỚI HẠN CỦA DÃY SỐ
- Slide 6
- Slide 7
- Slide 8
- Ví dụ 1:
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Ví dụ 2:
- Slide 15
- Slide 16
- LUYỆN TẬP
- Slide 18
- Slide 19
- Slide 20
- VẬN DỤNG
- Slide 22





