




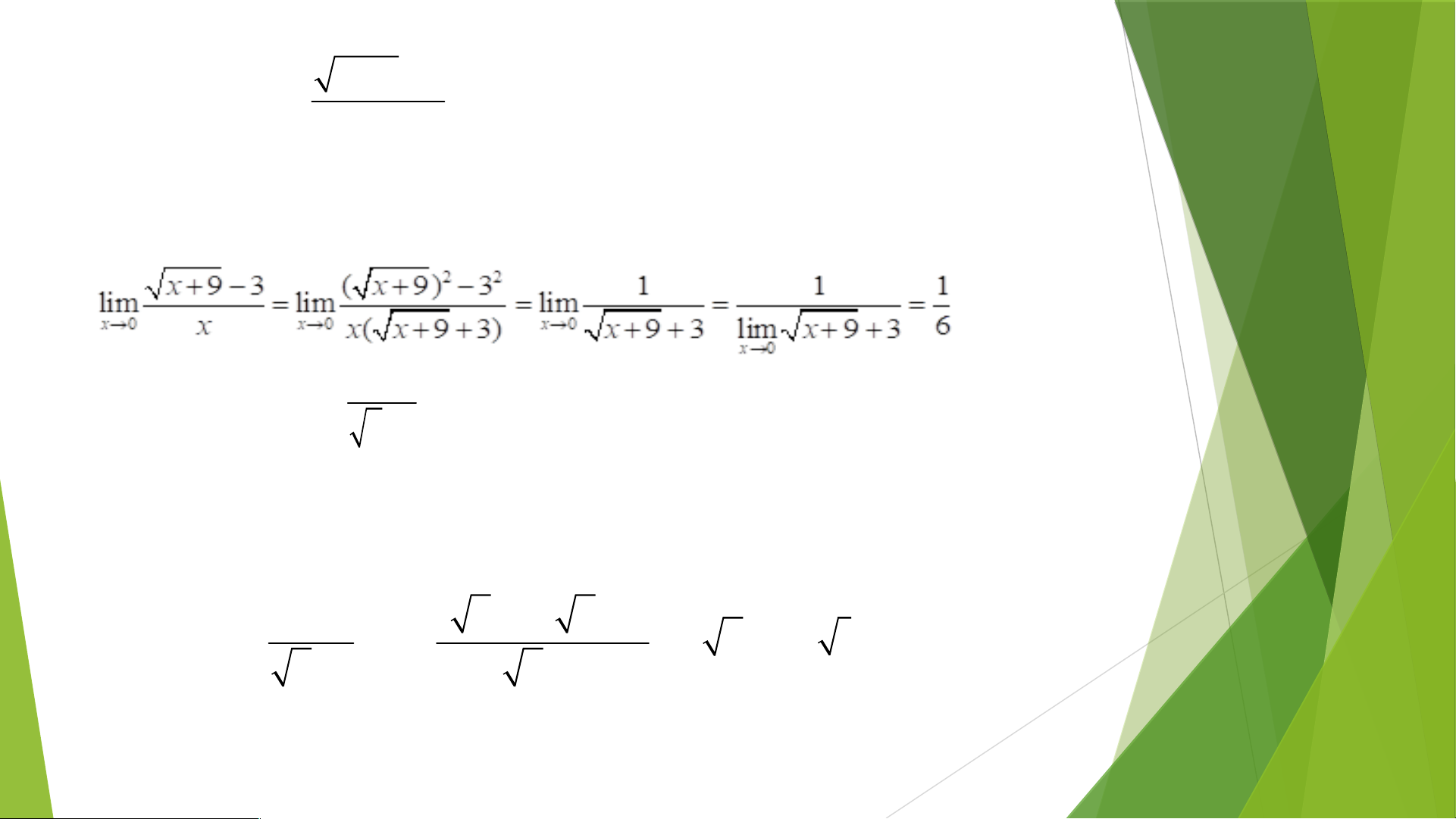







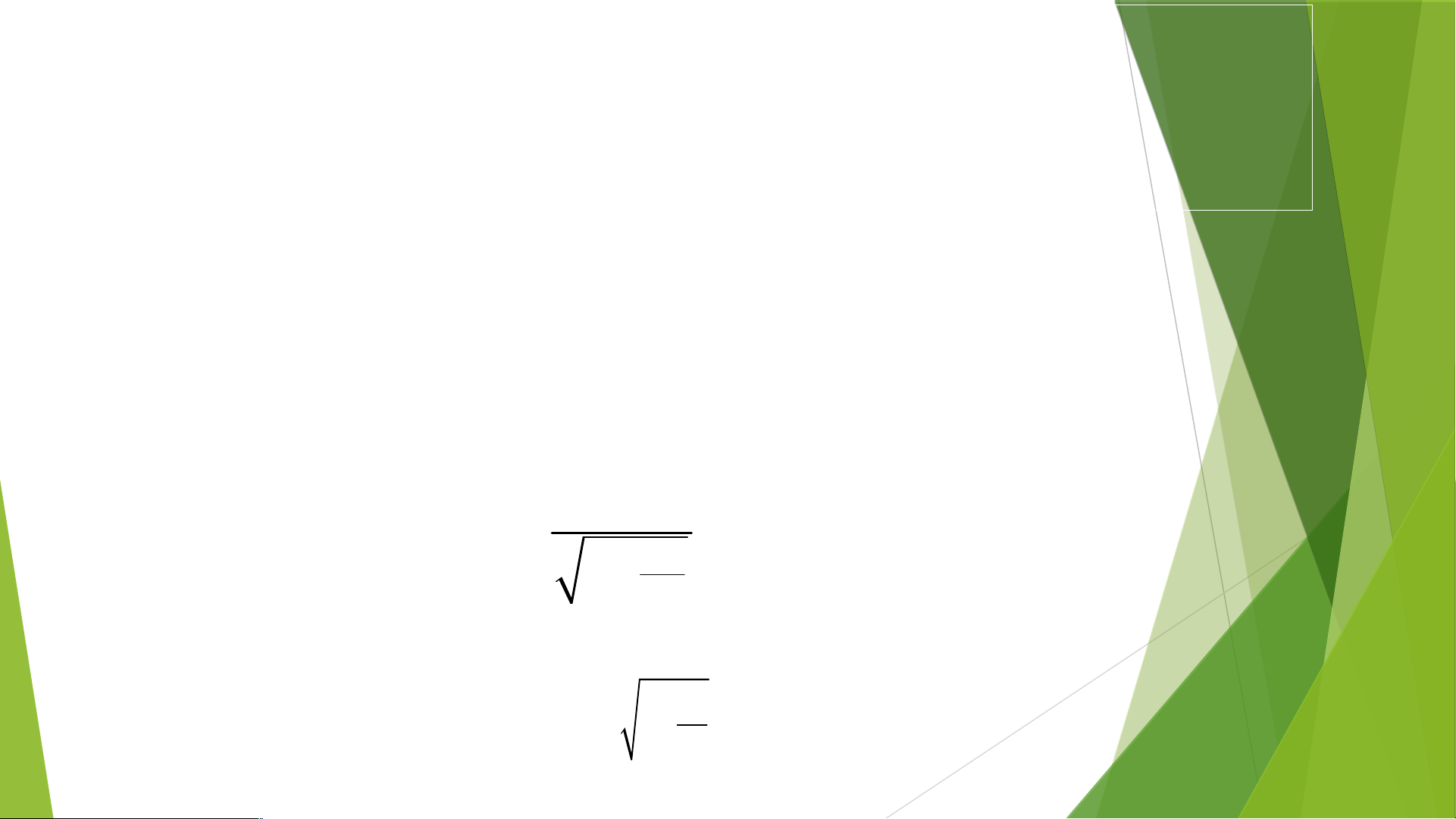








Preview text:
16
GIỚI HẠN CỦA HÀM SỐ
Trong Thuyết tương đối của Einstein, khối lượng của vật chuyển động với vận tốc v cho bởi công thức: m0 m
, trong đó m là khối lượng của vật khi nó đứng yên, c là vận tốc ánh sáng. 2 0 v 1 2c
Albert Einstein (1879 - 1955)
Chuyện gì xảy ra với khối lượng của vật khi vận tốc của vật gần với vận tốc ánh sáng?
1. GIỚI HẠN HỮU HẠN CỦA HÀM SỐ TẠI MỘT ĐIỂM
HĐ 1. Nhận biết khái niệm giới hạn tại một điểm 2 4 x
Cho hàm số f x . x 2
a) Tìm tập xác định của hàm số f x . 2n 1
b) Cho dãy số x
f x và tính giới hạn của dãy u với u f x . n . Rút gọn n n n n n
c) Với dãy số x bất kì sao cho x 2 và x 2, tính f x và tìm lim f x . n n n n n n Lời giải:
a) Biểu thức f(x) có nghĩa khi x – 2 ≠ 0 x ≠ ⇔ 2.
Do đó, tập xác định của hàm số f(x) là D = \ ℝ {2}. b) Ta có: 2 2n 1 1 4 1 1 1 4 2 4 2 4 4 4 2 2 4 x n n n n n n 1 f x 4 x 2 2n 1 1 1 1 2 n 2 2 n n n n
1. GIỚI HẠN HỮU HẠN CỦA HÀM SỐ TẠI MỘT ĐIỂM 2 2 2n 1 1 4 1 1 1 4 4 2 4 4 4 2 2 4 x n n n n n n 1 f x 4 x 2 2n 1 1 1 1 2 n 2 2 n n n n 1 lim u lim f (x ) lim 4 4 n n n n x n
c) Với dãy số x bất kì sao cho x 2 và x 2, tính f x và tìm lim f x . n n n n n n 2 4 x
(2 x )(2 x ) lim f (x ) n n n 2 x n x 2 (2 x ) n n n n
Vì x ≠ 2 và x ⟶ 2 với mọi n nê li n m x 2 n n n n
Do đó, lim f (x ) lim ( 2 x ) 2 2 4 n n n n
1. GIỚI HẠN HỮU HẠN CỦA HÀM SỐ TẠI MỘT ĐIỂM Giả sử ;
a b là một khoảng chứa điểm x và hàm số y f x xác định trên khoảng ;ab , có thể trừ 0
điểm x . Ta nói hàm số f x có giới hạn là số L khi x dần tới x nếu với dãy số x bất kì, n 0 0
x ;ab , x x và x x , ta có f x L , kí hiệu lim
f x L hay f x L khi x x . n n 0 n x x n 0 0 0 x 1 1
Ví dụ 1. Cho hàm số f x
. Chứng tỏ rằng lim f x . 2 x 1 x1 2 Lời giải x 1 1
Lấy dãy số x bất kì sao cho x 1 x . n f x . n n và 1 n Ta có n 2 x 1 x 1 n n 1 1 1
Do đó lim f x
. Vậy lim f (x) n lim . n
n x 1 2 x1 2 n
Quy tắc tính giới hạn của hàm số tại một điểm như sau:
a) Nếu lim f (x) L và lim g(x) M thì lim[ f (x) g(x)] L M ; lim[ f (x) g(x)] L M ; x 0 x x 0 x x 0 x x 0 x f (x) L
lim[ f (x).g(x)] . L M ; lim , nếu M 0 . x 0 x x 0 x g(x) M b) Nếu f (x) 0
với mọi x ( ;
a b) \ x và lim f (x) L thì L 0
lim f (x) L . 0 và x 0 x x 0 x
Ví dụ 2. Cho f (x) x 1 và 3
g(x) x . Tính các giới hạn sau: 2 [ f (x)]
a) lim[3 f (x) g(x)] b) lim x1 x1 g(x) Lời giải
Ta có lim f (x) l im(x 1) l im x lim1 1 1 0 . Mặt khác, ta thấy 3 lim g(x) l im x 1 . x1 x1 x1 x1 x1 x1
a) Ta có: lim[3 f (x) g(x)] l
im[3 f (x)] lim g(x) l
im 3.lim f (x) lim g(x) 3 .0 1 1. x1 x1 x1 x1 x1 x1 2 2 lim[ f (x)]
lim f (x).lim f (x) [ f (x)] 0 b) Ta có: x1 x 1 x1 lim 0 . x 1 g(x) lim g(x) lim g(x) 1 x 1 x1 x 9 3 Ví dụ 3. Tính lim . x 0 x Lời giải Ta có x 1
Luyện tập 1. Tính lim . x1 x 1 Lời giải Ta có x 1
( x 1)( x 1) lim l im lim x 1 1 1 2 x1 x1 x1 x 1 x 1
Hoạt động 2. Nhận biết khái niệm giới hạn một bên | x 1|
Cho hàm số f (x) . x 1 n n 1 a) Cho x và x
y f x và y f x . n . Tính n n n n n n 1 n
b) Tìm giới hạn của các dãy số y và y . n n
c) Cho các dãy số x và x bất kì sao cho x 1 x và x 1, x 1 , tính lim f x và n n n n n n n n
lim f x . n n Lời giải
a) Ta có: x = 1 - 1/n < 1 với mọi n > 0 => x - 1 < 0 với mọi n > 0. n n x 1 n (x 1)
Do đó: y f (x ) n 1 n n x 1 x 1 n n 1 Ta cũng có: với ' x 1 ' 1 x 1 0 n
mọi n > 0 => n với mọi n > 0. n ' ' x 1 n x 1 Do đó: ' '
y f (x ) n 1 n n ' ' x 1 x 1 n n
b) Tìm giới hạn của các dãy số y và y . n n Ta có: '
lim y lim ( 1) 1; lim y lim 1 1 n n n n n n c) Ta có:
Vì x < 1 < x' , suy ra x – 1 < 0 và x' – 1 > 0 với mọi n. n n n n
Do đó, f(x ) = – 1 và f(x' ) = 1. n n Vậy: '
lim f (x ) 1; lim f (x ) 1 n n n n
- Cho hàm số y f (x) xác định trên khoảng x ;b . Ta nói số L là giới hạn bên phải của f (x) khi x x 0 0
nếu với dãy số x bất kì thoả mã̃n x x b và x x , ta có f x L , kí hiệu lim f (x) L. n n 0 n n 0 x 0 x
- Cho hàm số y f (x) xác định trên khoảng ;
a x . Ta nói số L là giới hạn bên trái của f (x) khi x x nếu 0 0
với dãy số x bất kì thoả mãn a x x và x x , ta có f x L , kí hiệu lim f (x) L . n n n 0 n 0 x 0 x 2 x nÕu 0 x 1
Ví dụ 4. Cho hàm số f (x) x 1 n Õu1 x 2
Tính lim f (x) và lim f (x) . x 1 x 1 Lời giải
Với dãy số x bất kì sao cho 0 x 1 và x 1, ta có f x x . n n 2 n n n
Do đó lim f (x) lim f x 1 n . x1 n
Tương tự, với dãy số x bất kì mà 1 x 2, x 1, ta có f x x , cho nên n n 1 n n n
lim f (x) lim f x 2 n . x1 n
x nÕu x 0
Luyện tập 2. Cho hàm số f (x)
Tính lim f (x), lim f (x) và lim f (x) . x n Õ ux 0 x 0 x 0 x 0 Lời giải
Với dãy số (x ) bất kì sao cho x < 0 và x 0, t ⟶ a có f(x ) = – x . n n n n n Do đó: lim f( )
x lim f(x ) lim ( x ) 0 n n x 0 n n
Tương tự, với dãy số (x ) bất kì sao cho x > 0 và x 0, t ⟶ a có f(x ) = √x. n n n n Do đó: lim f( )
x lim f(x ) lim x 0 n n x 0 n n Khi đó: lim f( ) x lim f( ) x 0 x 0 x 0 Vậy: limf( ) x 0 x 0
2. GIỚI HẠN HỮU HẠN CỦA HÀM SỐ TẠI VÔ CỰC
Hoạt động 3. Nhận biết khái niệm giới hạn tại vô cực 2
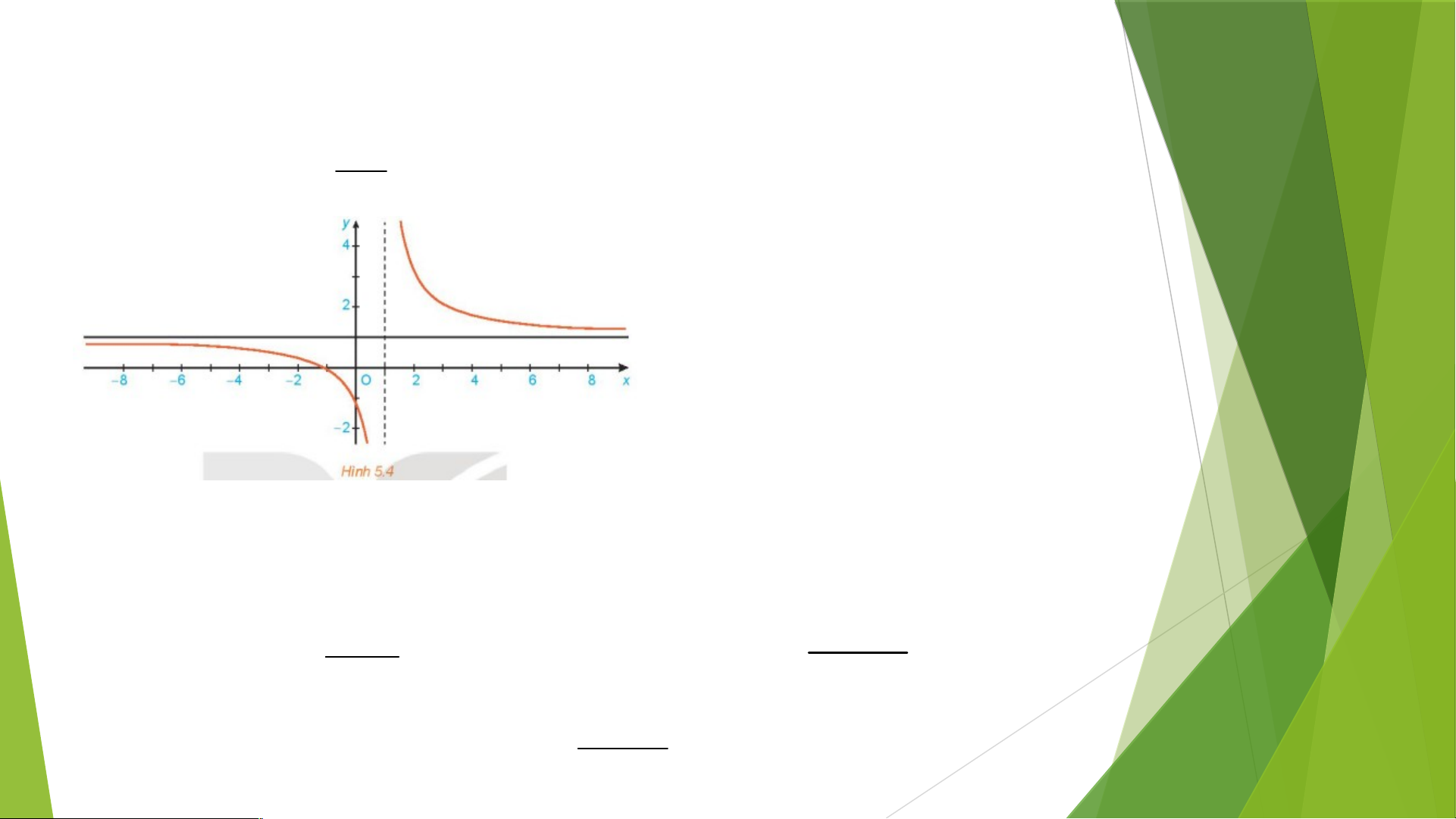
Cho hàm số f (x) 1
có đồ thị như Hình 5.4. x 1
Giả sử x là dãy số sao cho x 1, x
f x và tìm lim f x . n n n n . Tính n n Lời giải
Với (x ) là dãy số sao cho x > 1, x + ⟶ ∞. n n n 2 2 Ta có: f( ) n 1 Khi x ⟶ +∞ thì lim 0 n x 1 x x 1 n n 2 Do đó: lim f( ) n lim 1 1 x x x 1 n
- Cho hàm số y f (x) xác định trên khoảng ( ; a )
. Ta nói hàm số f (x) có giới hạn là số L khi x
nếu với dãy số x bất kì, x x
f x L . kí hiệu lim f (x) L hay f (x) L khi n
n a và n , ta có n x x .
- Cho hàm số y f (x) xác định trên khoảng ( ;
b) . Ta nói hàm số f (x) có giới hạn là số L khi x nếu
với dãy số x bất kì, x b và x
f x L , kí hiệu lim f (x) L hay f (x) L khi n n n , ta có n x x . 4
Ví dụ 5. Cho f (x) 2
. Sử dụng định nghĩa, tìm lim f (x) và lim f (x) . x 1 x x Lời giải 4
Lấy dãy x bất kì sao cho x 1 và x f x 2 . Do đó lim f x 2 n n . n n , ta có
n x 1 n n
Vậy lim f (x) 2
. Tương tự, ta cũng có lim f (x) 2 x x
- Các quy tắc tính giới hạn hữu hạn tại một điểm cũng đúng cho giới hạn hữu hạn tại vô cực.
- Với c là hằng số, ta có: lim c c , lim c c . x x 1 1
- Với k là một số nguyên dương, ta có: lim 0 , lim 0 . k k x x x x 2 x 1 Ví dụ 6. Tính lim . x x Lời giải 2 2 x 1 x 1 1 1 1 Ta có lim lim lim 1 lim 1 1 lim 1 . 2 2 x 2 2 x x x x x x x x x 2 x 2
Luyện tập 3. Tính lim . x x 1 Lời giải 2 2 2 Ta có: 2 x 1 2 2 x 1 1 2 2 x 2 x x x 1 lim lim lim lim 1 x x 1 x x 1 x 1 x 1 1 x 1 1 x x
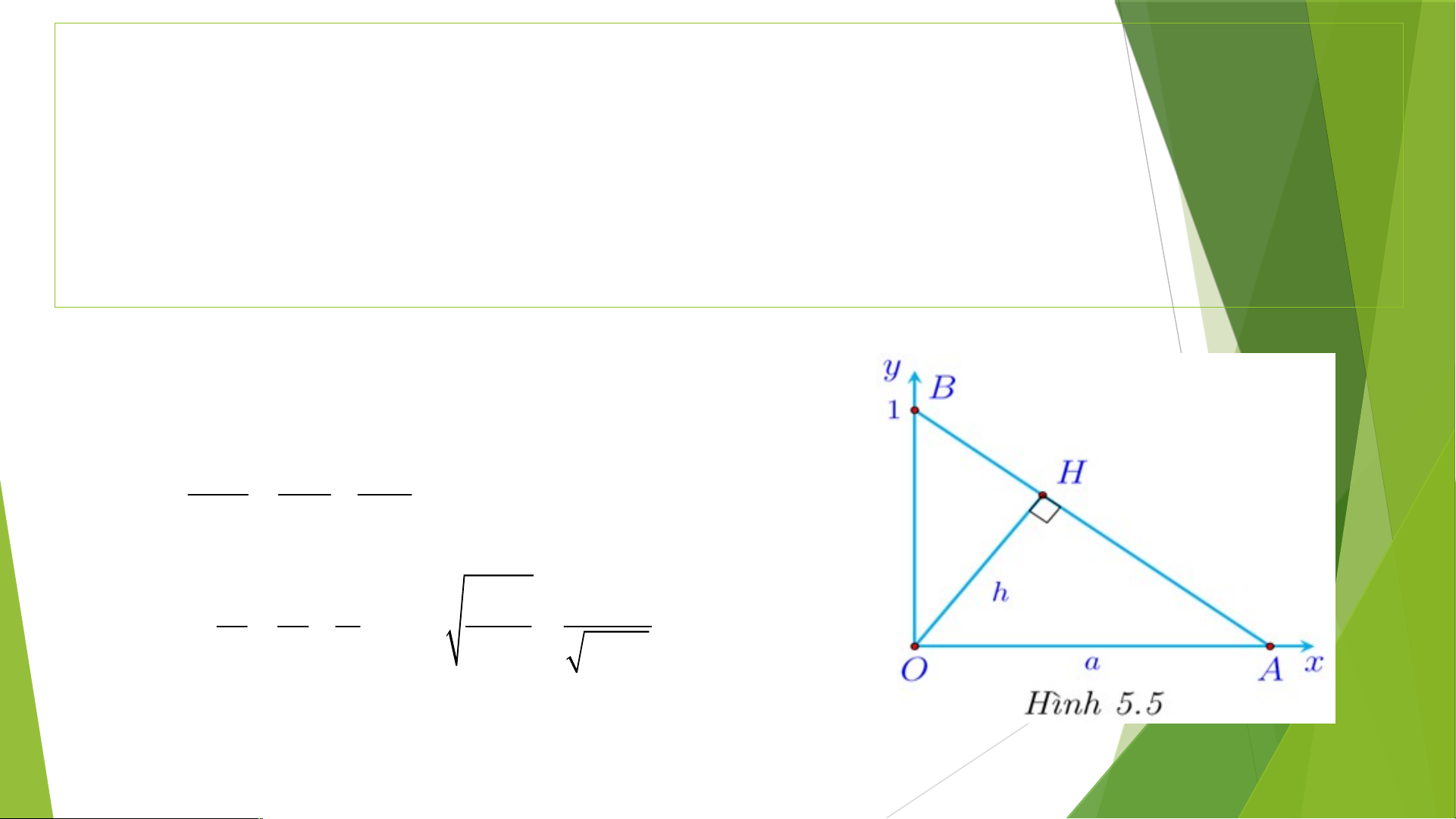
Vận dụng. Cho tam giác vuông OAB với A
a ;0 và B 0;
1 như Hình 5.5. Đường cao OH có độ dài là h .
a) Tính h theo a .
b) Khi điểm A dịch chuyển về O , điểm H thay đổi thế nào? Tại sao?
c) Khi A dịch chuyển ra vô cực theo chiều dương của trục Ox , điểm H thay đổi thế nào? Tại sao? Lời giải a) Ta có: A = (a; 0) O ⇒ A = a; B = (0; 1) O ⇒ B = 1
Tam giác OAB vuông tại O có đường cao OH nên ta có 1 1 1 2 2 2 OH OA OB Do đó, 2 1 1 1 a a h 2 2 2 2 2 h a 1 a 1 a 1
b) Khi điểm A dịch chuyển về O, ta có OA = a = 0, suy ra h = 0, do đó
điểm H dịch chuyển về điểm O.
c) Khi A dịch chuyển ra vô cực theo chiều dương của trục Ox, ta có OA = a + ⟶ ∞. Ta có: 2 2 a a 1 lim h lim lim lim 1 2 a a
a 1 a 1 a 1 2 a 1 1 2 2 a a
Do đó, điểm H dịch chuyển về điểm B.
3. GIỚI HẠN VÔ CỰC CỦA HÀM SỐ TẠI MỘT ĐIỂM
a) Giới hạn vô cực 1 1
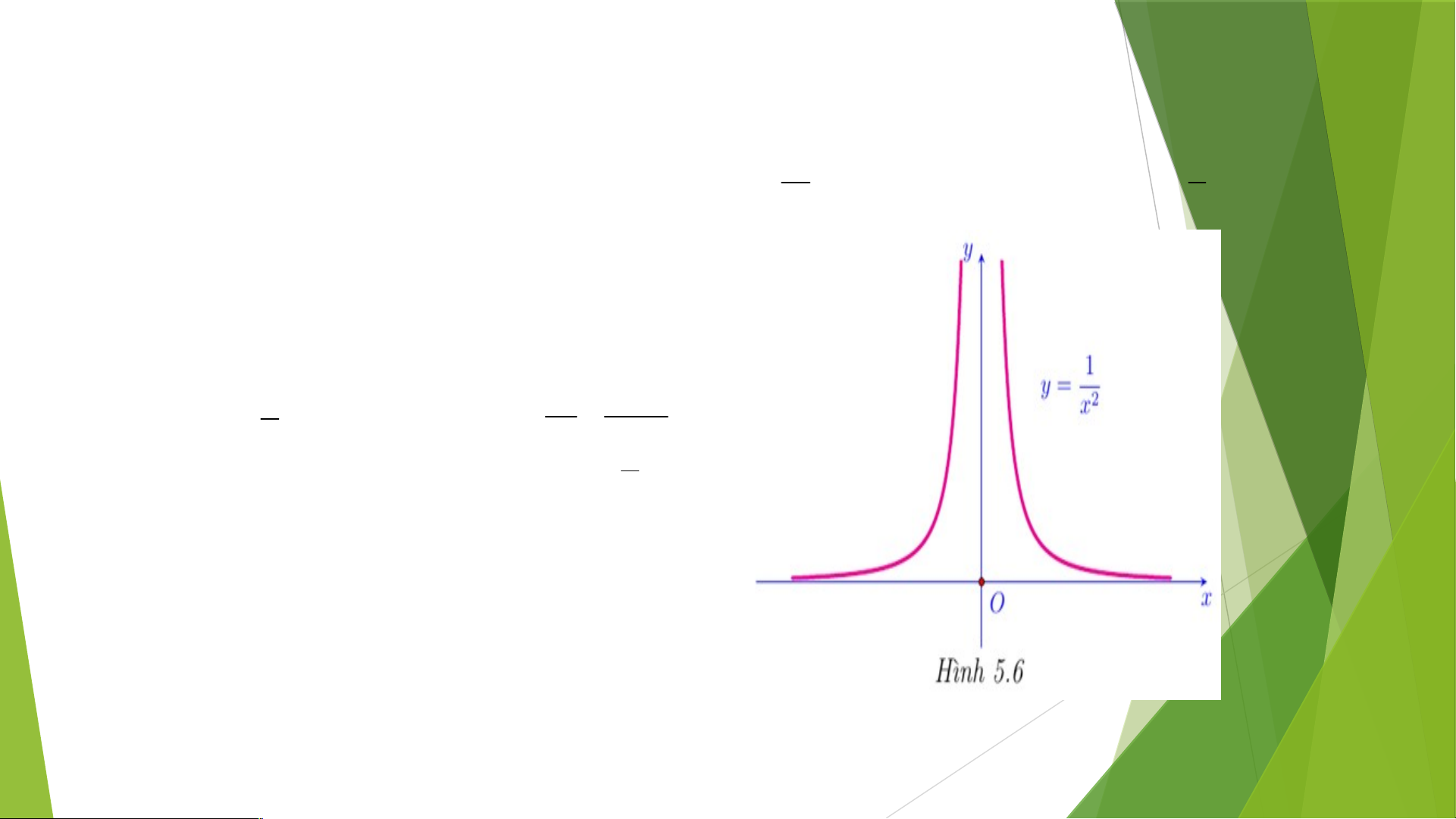
HĐ4. Nhận biết khái niệm giới hạn vô cực. Xét hàm số f x có đồ thị như Hình 5.6. Cho x , 2 x n n
chứng tỏ rằng f xn . Lời giải: 1 1 1 Ta có: xn do đó 2 f(x ) n n 2 2 n xn 1 n Vì n ⟶ +∞ nên
x →0 và f(x ) ⟶ +∞. n n 1 Ví dụ 7. Tính lim . x1 x 1 Lời giải: 1
Xét hàm số f x
. Lấy dãy số x bất kì sao cho x 1 x
. Khi đó, x 1 0 . n , 1 x n n n 1 1 1 Do đó f x . Vậy lim . n x 1 x1 x 1 n 1 1 1
HĐ5. Cho hàm số f x
. Với các dãy số x và x x 1 x 1 n
n cho bởi , , tính x n n 1 n n
lim f x và lim f x n n . n n Lời giải: 1 1 1
Ta có: lim f (x ) lim lim lim lim n n n
n x 1 n 1 n 1 n n 1 1 n n 1 1 1 '
lim f (x ) lim lim lim
lim ( n) n ' n
n x 1 n 1 n 1 n n 1 1 n n
Cho hàm số y f x xác định trên khoảng x ;b . Ta nói hàm số f (x) có giới hạn 0 khi
x x về bên phải nếu với dãy số x bất kì thoả mãn x x b , x x , ta có f x 0 n 0 n n 0 n
, kí hiệu lim f x . x 0 x
Cho hàm số y f x xác định trên khoảng ;
a x . Ta nói hàm số f (x) có giới hạn 0 khi
x x về bên trái nếu với dãy số x bất kì thoả mãn a x x , x x , ta có f x n n 0 n 0 n 0
, kí hiệu lim f (x) . x 0 x
Các giới hạn một bên lim f x và lim f x được định nghĩa tương tự. x 0 x x 0 x
Ví dụ 8. Giải bài toán ở tình huống mở đầu. Lời giải:
Từ công thức khối lượng m0 m 2 v 1 2 c
ta thấy m là một hàm số của v , với tập xác định là nửa khoảng 0;c . Rõ ràng khi v tiến gần 2 v
tới vận tốc ánh sáng, tức là v c , ta có 1
0 . Do đó lim m v , nghĩa là khối 2 c v c
lượng m của vật trở nên vô cùng lớn khi vận tốc của vật gần với vận tốc ánh sáng.
Luyện tập 4. Tính các giới hạn sau: 2 1 a) lim ; b) lim . x 0 x x 2 2 x Lời giải: 2 a) Xét hàm số f ( x) . Lấy dãy số bấ x t kì sao cho x 0 , x 0. x n n n 2 2
Do đó, f (x) Vậy lim x x 0 x 1 b) Đặt . g(x) Với mọi dãy số t
xn rong khoảng (– ∞; 2) mà lim x 2 n x 2 x 1
ta có lim g(x) lim n n 2 x 1 Vậy
lim g ( x) lim x 2 x 2 2 x
Chú ý. Các giới hạn lim f x ,
lim f x , lim f x và lim f x được x x x x
định nghĩa tương tự như giới hạn của hàm số f x tại vô cực. Chẳng hạn: Ta nói hàm số f x
xác định trên khoảng ;
a , có giới hạn là khi x x bất kì,
n nếu với mọi dãy số n
x a và x , ta có f x lim f x f x
n , kí hiệu
khi x n n hay x
. Một số giới hạn đặc biệt: lim k
x Với k nguyên dương; x lim k
x với k là số chẵn; x lim k
x với k là số lẻ. x
b) Một số quy tắc tính giới hạn vô cực
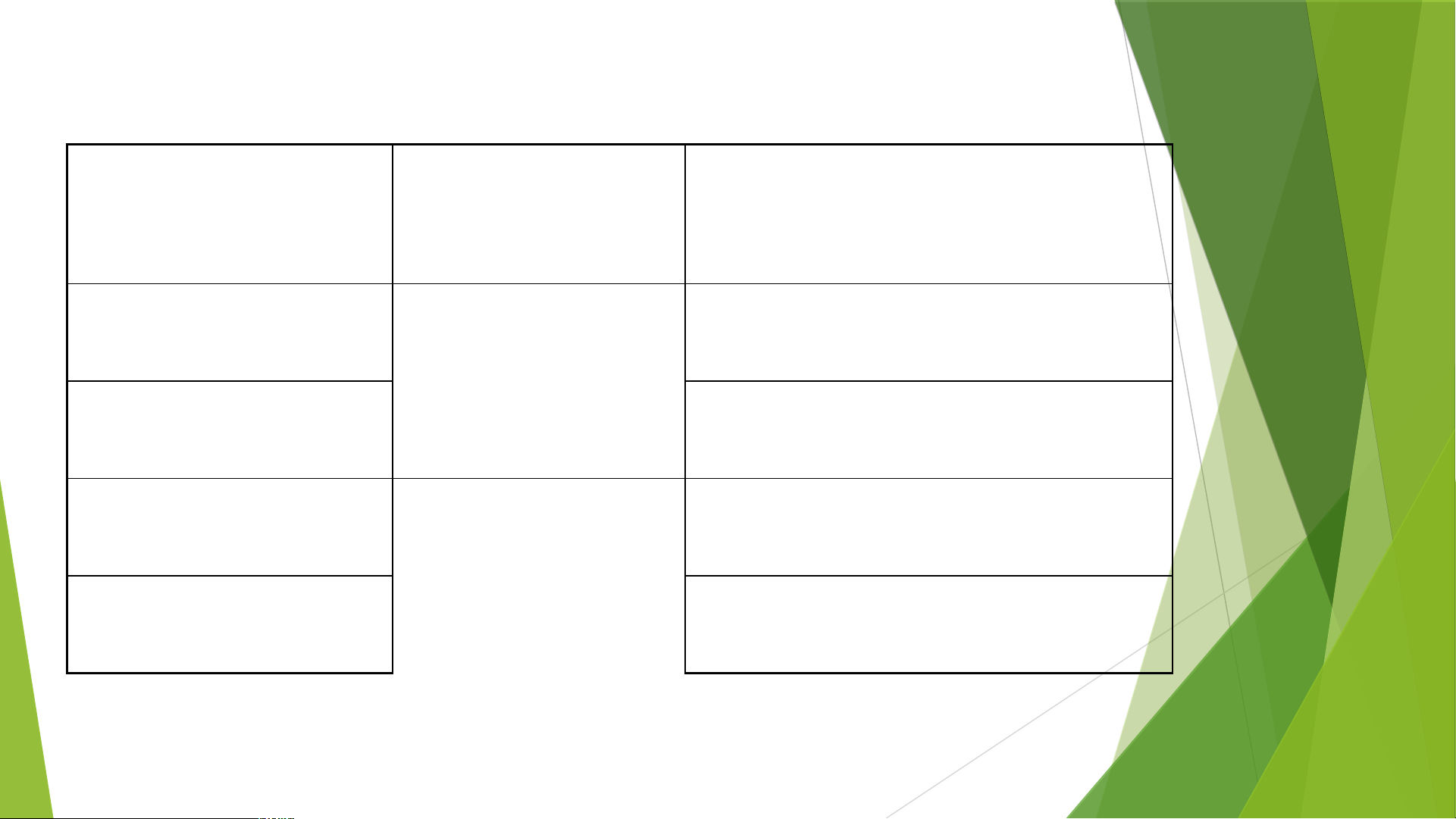
Quy tắc tìm giới hạn của một tích:
b) Quy tắc tìm giới hạn của một thương: Dấu của Tùy ý 0 0
Các quy tắc trên vẫn đúng trong các trường hợp x 1 Ví dụ 9. Tính lim . 2 x 0 x Lời giải:
Ta sử dụng quy tắc tìm giới hạn của thương. Rõ ràng, giới hạn của tử số lim x 1 1 . x 0 x 1
Ngoài ra, mẫu số nhận giá trị dương với mọi x 0 và 2 lim x 0 . Do vậy lim . x 2 0 x 0 x 1 1 Ví dụ 10. Tính lim và lim . x 1 x 1 x x 1 x 1 x Lời giải: 1 1 1 1 1 Viết , ta có lim 1 0 . Hơn nữa lim
do 1 x 0 khi x 1.
x1 x x 1 x x 1 x x 1 1 x 1
Áp dụng quy tắc tìm giới hạn của tích, ta được lim . x 1 x1 x 1
Lí luận tương tự, ta có lim .
x1 x1 x 2x 1 2x 1
Luyện tập 5. Tính lim và lim . x 2 x 2 x 2 x 2 Lời giải: a)Ta có: lim (2 x) 0
, x 2 0 x 2 x 2 lim (2x 1) 3 0 x 2 2x 1 Do đó: lim x 2 x 2 b)Ta có: lim (x 2) 0
, x 2 0 x 2 x 2 lim (2x 1) 3 0 x 2 2x 1 Do đó: lim x 2 x 2 Bài tập 2 x 1
5.7. Cho hai hàm số f (x)
và g(x) x 1. Khẳng định nào sau đây là đúng? x 1
a) f (x) g(x) ;
b) lim f (x) l
im g(x) . x1 x1 Lời giải:
a) Biểu thức f(x) có nghĩa khi x – 1 ≠ 0 x ≠ ⇔ 1. 2
x 1 (x 1)(x 1) Ta có: với f (x) x 1 mọi x ≠1 x 1 x 1
Biểu thức g(x) = x + 1 có nghĩa với mọi x.
Do đó, điều kiện xác định của hai hàm số f(x) và g(x) khác nhau, vậy khẳng định a) là sai. 2 x 1
(x 1)(x 1) b) Ta có: lim f (x) l im l im l im(x 1) 1 1 2 x1 x1 x1 x1 x 1 x 1 lim g(x) l im(x 1) 1 1 2 Vậy: n lim f (x) l im g(x) ên câu b) đúng. x1 x1 x1 x1
5.8. Tính các giới hạn sau: 2 (x 2 2) 4 x 9 3 a) lim b) lim . x 2 0 x x 0 x Lời giải: 2 (x 2) 4
x 2 2 x 2 2 x(x 4) a) Ta có: lim l im l im l im(x 4) 0 4 4 x 0 x 0 x 0 x 0 x x x 2 2 2 2 b) Ta có: x 9 3
( x 9 3)( x 9 3) x 9 9 lim l im l im x 0 x 0 2 2 x 0 2 2 x x ( x 9 3) x ( x 9 3) 2 x 1 1 1 l im l im x 0 2 2 x 0 2 x ( x 9 3) x 9 3 0 9 3 6
5.10. Tính các giới hạn một bên: x 2 2 x x 1 a) lim ; b) lim x 1 x 1 x 4 4 x a) Ta có: lim(x 1) 0
, x 1 0 x 1 x 1 lim(x 2) 1 2 1 0 x 1 x 2 Do đó: lim x 1 x 1 b) Ta có: lim (4 x) 0
, 4 x 0 x 4 x 4 2
lim (x x 1) 1 6 4 1 1 3 0 x 4 2 x x 1 Do đó: lim x 4 4 x 2 x 5x 6
5.11. Cho hàm số g(x)
. Tìm lim g(x) và lim g(x) . | x 2 | x 2 x 2 a) Ta có:
Do đó: l i m
g ( x ) l i m ( x 3) 2 3 1 x 2 x 2
lim g(x) lim (3 x) 3 2 1 x 2 x 2
5.12. Tính các giới hạn sau: 1 2x a) lim b) . 2 lim x x 2 x x x 2 x 1 1 1 x 2 2 1 2x x 2 x a) Ta có: lim lim lim 2 x 2 x 1 x 1 x 1 1 x 1 1 2 2 x x
2x x2 x 2x x2 x 2 b) Ta có: lim
x x x x 2 lim x 2
x x 2 x 2 2
x x 2 x x 2 lim lim x 2 x 2
x x 2 x
x x 2 x
2x x2 x 2x x2 x 2 lim
x x x x 2 lim x 2
x x 2 x 2 2
x x 2 x x 2 lim lim x 2 x 2
x x 2 x
x x 2 x 2 2 x 1 1 x 1 lim lim x x 1 2 x 1 2 2 x 1 1 1 1 2 2 x x x x 2
5.13. Cho hàm số f (x)
. Tìm lim f (x) và lim f (x) .
(x 1)(x 2) x 2 x 2 a)Tinh lim f (x) x 2 Ta có: 2 2 1 2 1 lim f (x) lim lim . lim . lim x 2 x 2 x 2 x 2 x 2
(x 1)(x 2) x 1 x 2 x 1 x 2 2 2 1 Vì: l i m x 2 0, x 2 2 0; li m do x 2 x 2 x 1 2 1 x 2
b) Tính lim f (x) x 2 Ta có: 2 2 1 2 1 lim f (x) lim lim . lim . lim x 2 x 2 x 2 x 2 x 2
(x 1)(x 2) x 1 x 2 x 1 x 2 2 2 1 Vì: d lim 2 0; lim x 2 0, x 2 o x 2 x 2 x 1 2 1 x 2
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27
- Slide 28
- Slide 29
- Slide 30
- Slide 31




