Giáo án điện tử Toán 11 Bài 17 Kết nối tri thức: Hàm số liên tục

17 HÀM SỐ LIÊN TỤC
Một người lái xe từ địa điểm A đến địa điểm B trong
thời gian 3 giờ.Biết quãng đường từ A đến B dài 180 km .
Chứng tỏ rằng có itt nhất một thời điểm trên hành trình,
xe chạy với vận tốc 60 km / h .
1. HÀM SỐ LIÊN TỤC TẠI MỘT ĐIỂM
HĐ1. Nhận biết tính liên tục của hàm số tại một điểm  x2  1  nÕux 1
Cho hàm số f (x)   x  1 2 nÕux  .  1
Tính giới hạn lim f (x) và so sánh giá trị này với f (1) . x 1 Lời giải: Ta có: f(1) = 2. 2 x  1  x   1  x   1 lim f (x) l  im  l  im l  im(x 1) 1  1 2  x 1 x 1 x 1 x 1 x  1 x  1
VËylim f (x)  f ( ) 1 x 1
1. HÀM SỐ LIÊN TỤC TẠI MỘT ĐIỂM
Cho hàm số y  f (x) xác định trên khoảng ( ;
a b) chứa điểm x f x x 0 . Hàm số
( ) được gọi là liên tục tại điểm 0
nếu lim f (x)  f  x0  . x 0x x 1
Ví dụ 1. Xét tính liên tục của hàm số f (x)  tại điểm x 2  . x 0  1 Lời giải:
Rõ ràng hàm số f (x) xác định trên  \{1}, do đó x 2
0  thuộc tập xác định của hàm số. x 1
Ta có lim f (x) l  im 3
  f (2) . Vậy hàm số f (x) liên tục tại x 2  . x 0  2 x 2 x  1
1. HÀM SỐ LIÊN TỤC TẠI MỘT ĐIỂM 1  nÕux  0
Ví dụ 2. Xét tính liên tục của hàm dấu s(x)  0 nÕux 0  tại điểm x 0 0  .  1 nÕux  0  Lời giải
Ta thấy lim s(x) 1
 , lim s(x)  1. Do đó không tồn tại x 0 x 0  
giới hạn lim s(x) . x 0
Vậy hàm số này gián đoạn tại 0 .  x nÕu x  0
Luyện tập 1. Xét tính liên tục của hàm số f (x)  0 nÕux 0  tại điểm x 0 0  .  2 x nÕux  0  Lời giải
Hàm số f(x) xác định trên , do đó x ℝ
= 0 thuộc tập xác định của hàm số. 0 2 2
Ta cã: lim f (x) lim x 0  0
 ; lim f ( x) lim ( x) 0  x 0 x 0 x 0 x 0     Do ® ã: lim f (x) lim f (x) 0  , suy ra lim f (x) 0  x 0 x 0 x 0 Mµ: f (x) 0
 , nªnlim f (x)  f (0).VËy hµm sè f (x) liªn tôc t¹i ® iÓmx 0 x 0
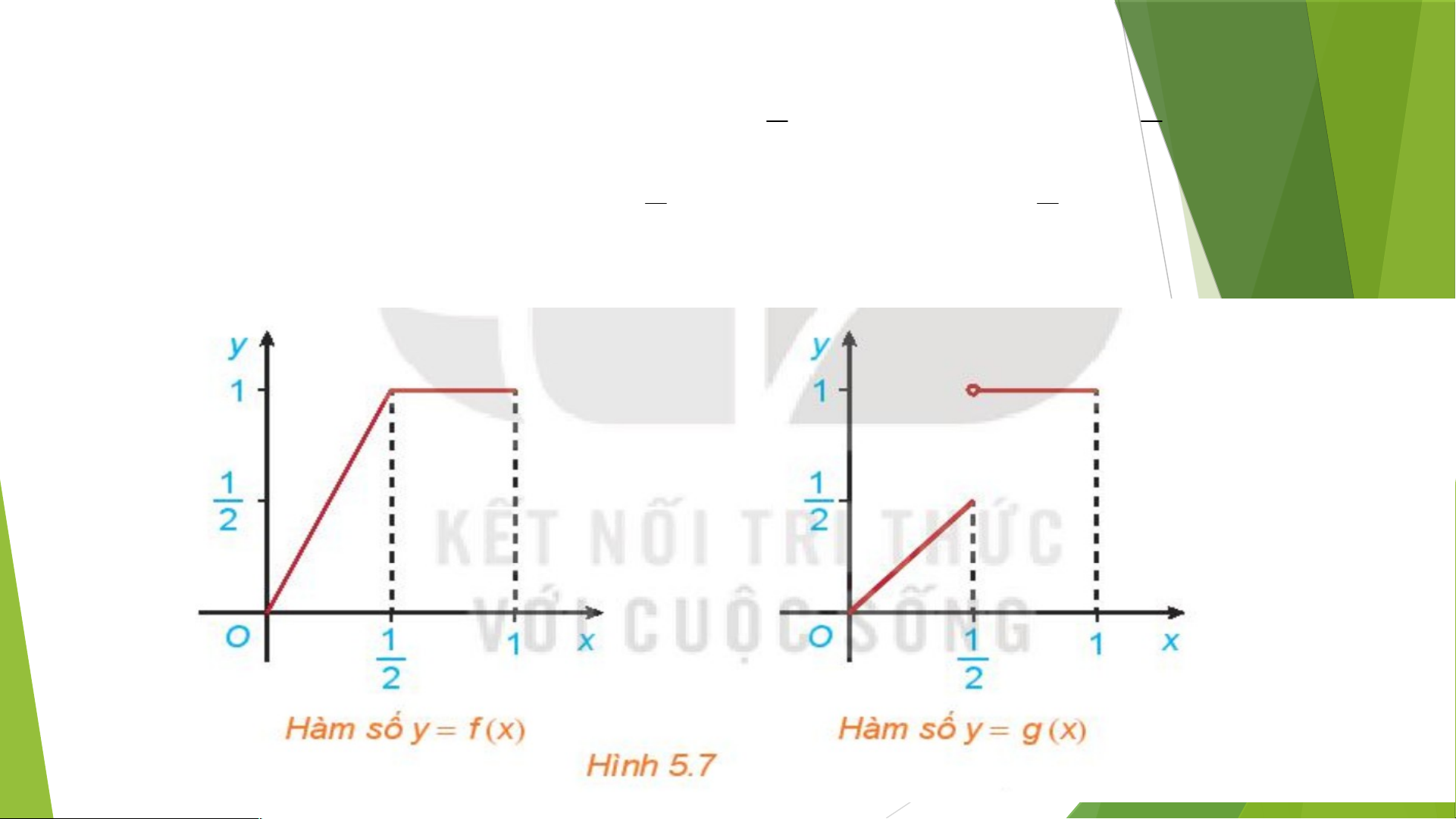
2. HÀM SỐ LIÊN TỤC TRÊN MỘTKHOẢNG  1  1 2x nÕu 0 x  x nÕu 0 x    HĐ2. Cho hai hàm số  2  2 f (x)  vµg (x)  1  1 1  nÕu x 1 1    nÕu  x 1    2   2
với đồ thị tương ứng như Hình 5.7
2. HÀM SỐ LIÊN TỤC TRÊN MỘTKHOẢNG Lời giải  1 2x nÕ u 0 x    2 + Hµm sè f (x)    1 1 nÕu  x 1    2 1
Hµm sècã TX§ trªn [0;1] do ® ã x
 thuéc TX§ cña hµm sè. 2 1
Ta cã: lim f (x)  lim 1 1
 ; lim f (x)  lim (2x) 2  . 1  1  1  1  1  2 x x x x 2 2 2 2
Suy ra: lim f (x)  lim f (x) 1  , Do ® ãlim f (x) 1    1 1 1 x x x    2 2 2  1  1  1  1 Mµ: f 2  . 1
 , nªnlim f (x)  f .VËy hµm sè f (x) liªn tôc t¹i ® iÓmx    1 2 2     x  2  2 2  1 x nÕu 0 x    2 + Hµm sè ( g x)  1 1  nÕu  x 1    2 1
Hµm sècã TX§ trªn [0;1] do ® ã x
 thuéc TX§ cña hµm sè. 2 1
Ta cã: lim g(x)  lim 1 1
 ; lim g(x)  lim x  1  1  1  1  2 x x x x 2 2 2 2
Suy ra: lim g(x)  lim g(x) 1.  1  1  x x 2 2 1
VËy kh«ng tån t¹i gií i h¹n cña hµm sè ( g x) liªn tôc t¹i ® iÓmx  . 2 1 Do ®ã hµm sè ( g x) gi¸n ® o¹n t¹ x i 2
Hàm số y  f (x) được gọi là liên tục trên khoảng ( ;
a b) nếu nó liên tục tại mọi điểm thuộc khoảng này.
Hàm số y  f (x) được gọi là liên tục trên đoạn [a ; b] nếu nó liên tục trên khoảng (a;b) và .
lim f (x)  f (a), lim f (x)  f (b) . x a x b    x 1 neá u x 0; 1
Ví dụ 3. Xét tính liên tục của hàm số f   x 
trên nửa khoảng  0;  1 .  0 neáu x   1 Lời giải Ta có f  
x x 1 với x 0; 1 . Với x  0;1 bất kì, ta có lim x  1 x  1 f x . 0     0  0  x 0 x
Vậy hàm số f  x liên tục trên khoảng  0;  1 .
Hơn nữa, lim f  x 0   f  
1 nên f  x liên tục trên nửa khoảng  0; 1 . x 1  
Về tính liên tục của các hàm số sơ cấp cơ bản đã biết, ta có
 Hàm số đa thức và các hàm số y s  in x, y c
 os x liên tục trên  .
 Các hàm số y tan x, y c
 ot x, y  x và hàm phân thức hữu tỉ (thương của hai đa thức) liên
tục trên tập xác định của chúng. x 1
Ví dụ 4. Cho hàm số f  x 
. Tìm các khoảng trên đó hàm số f  x liên tục. x  1 Lời giải
Tập xác định của hàm số f  x là    
;1 1; . Vậy hàm số f  x liên tục trên các khoảng   ;   1 và 1; . 2 x 1
Luyện tập 2. Tìm các khoảng trên đó hàm số f  x  liên tục. x  2 Lời giải
TXĐ hàm số f(x) là (–∞; – 2) (– 2; ∪ +∞).
Vậy hàm số f(x) liên tục trên các khoảng (–∞; – 2) và (– 2; +∞).
3. MỘT SỐ TÍNH CHẤT CƠ BẢN
HĐ3. Cho hai hàm số   2
f x x và g  x  x 1.
a) Xét tính liên tục của hai hàm số trên tại x 1  . b) Tính L l
 im  f  x  g  x  và so sánh L với f   1  g  1 . x    1 Lời giải:
a) Hàm số f(x) = x2 và g(x) = – x + 1 là các hàm đa thức nên nó liên tục trên . ℝ
Do đó, hai hàm số f(x) và g(x) đều liên tục tại x = 1.
b) Ta có: f(x) + g(x) = x2 + (– x + 1) = x2 – x + 1. Do ® ã: L l = im f (x)  g(x) 2 2 l  im(x  x 1) 1   1 1 1  x 1 x 1
Lại có, f(1) = 12 = 1; g(1) = – 1 + 1 = 0, do đó f(1) + g(1) = 1 + 0 = 1. Vậy L = f(1) + g(1) = 1.
Ta có khẳng định sau đây về tổng, hiệu, tích và thương của hai hàm số liên tục.
Giả sử hai hàm số y  f  x và y g  x liên tục tại điểm x . Khi đó: 0
a) Các hàm số y  f  x  g  x , y  f  x  g  x và y  f  x g  x liên tục tại x ; 0 f  x b) Hàm số y 
liên tục tại x nếu g  x 0 0   . g  x 0 sin x
Ví dụ 5. Xét tính liên tục của hàm số f  x  . x  1 Lời giải
Hàm số xác định trên các khoảng   ;  
1 và 1; . Trên các khoảng này, tử thức (hàm lượng giác) và
mẫu thức (hàm đa thức) là các hàm số liên tục. Do đó, hàm số f  x liên tục trên  \ 1 .
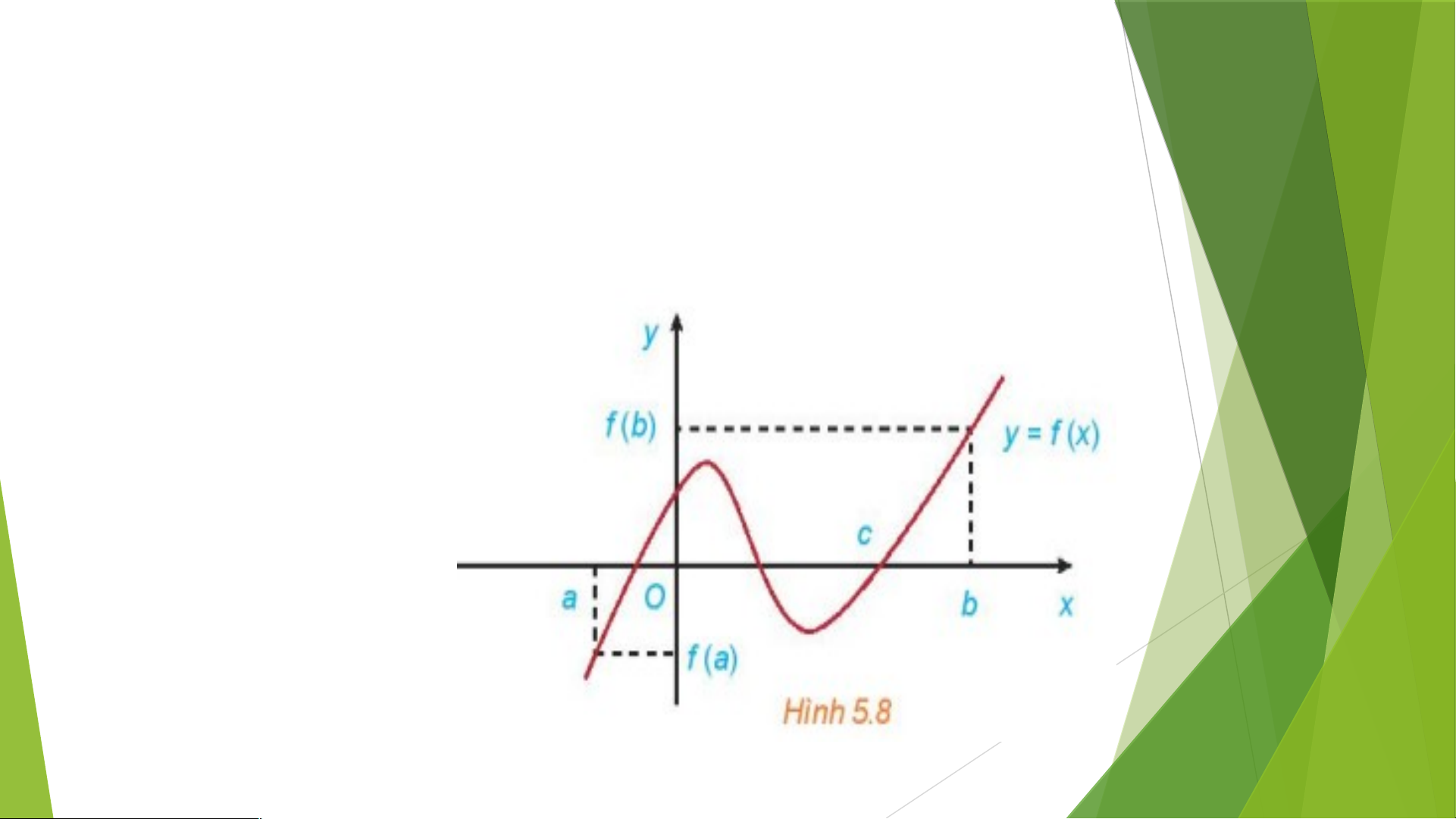
Nhận xét. Nếu hàm số y  f  x liên tục trên đoạn  ;
a b và f  a f b  0 thì tồn tại ít nhất một đi
c a;b sao cho f  c 0  .
Kết quả này được minh hoạ bằng đồ thị như Hình 5.8 xn
Vận dụng. Giải bài toán ở tình huống mở đầu. Lời giải:
Theo giả thiết, vận tốc trung bình của xe là v = 16031603 = 60 (km/h). a
Gọi v(t) là hàm biểu thị vận tốc của xe tại thời điểm t.
Tại thời điểm xuất phát t , vận tốc của xe v(t ) = 0 nên có một thời điểm t xe chạy với vận 0 0 1 tốc v(t ) > v . 1 a
Xét hàm số f(t) = v(t) – v , rõ ràng f(t) là hàm số liên tục trên đoạn [t ; t ]. a 0 1
Hơn nữa, ta có f(t ) = – v < 0, f(t ) = v(t ) – v > 0 (do v(t ) > v ), nên tồn tại thời điểm 0 a 1 1 a 1 a
t* thuộc khoảng (t ; t ) sao cho f(t*) = 0. Khi đó ta có v(t*) – v = 0 hay v(t*) = v = 60. 0 1 a a
Vậy có ít nhất một thời điểm trên hành trình, xe chạy với vận tốc 60 km/h. BÀI TẬP
5.14. Cho f  x và g  x là các hàm số liên tục tại x 1  . Biết f   1 2
 và lim  2 f  x  g  x  3  g . x   . Tính   1  1 Lời giải:
Vì hàm số f(x) liên tục tại x = 1 nên hàm số 2f(x) cũng liên tục tại x = 1.
Mà hàm số g(x) liên tục tại x = 1. Do đó, hàm số y = 2f(x) – g(x) liên tục tại x = 1. Suy ra: L l = im 2f (x)  g(x) 2  f (1)  g(x) x 1 V× : L l = im 2f (x)  g(x) 3  vµf (1) 2
 nªn ta cã 3 = 2.2 - g(1)  g(1)=1 x 1 VËy g(1)=1
5.15. Xét tính liên tục của các hàm số sau trên tập xác định của chúng: x  2 1 x neáu x 1 a) f     x  .
b) f  x  . 2 x   5x  6 4 x neáu x  1 Lời giải: ) x
a f  x  2 x 5x 6 x  x  2 BiÓu thøcf  x 2  cã nghÜa khi x  5x  6 0 2   x 5x 6  x  3  TXĐ hàm số f(x) là \
ℝ {– 3; – 2} = (–∞; – 3) (– ∪ 3; – 2) (– 2; ∪ +∞).
Vì f(x) là hàm phân thức hữu tỉ nên nó liên tục trên tập xác định.
Vậy hàm số f(x) liên tục trên các khoảng (–∞; – 3), (– 3; – 2) và (– 2; +∞).
5.15. Xét tính liên tục của các hàm số sau trên tập xác định của chúng: x  2 1 x neáu x 1 a) f     x  .
b) f  x  . 2 x   5x  6 4 x neáu x  1 Lời giải:  2 1 x neáu x 1 ) b f      x   4 x neáu x 1   
Ta cã:lim f (x) lim(4  x) 4   1 3 
Tập xác định của hàm số là . ℝ x 1 x 1  
+) Nếu x < 1, thì f(x) = 1 + x2. 2 2 lim f (x) lim(1 x ) 1  1 2   
Đây là hàm đa thức nên có tập xác định là . ℝ x 1 x 1 Suy ra:lim f (x) lim f (x)
Vậy nó liên tục trên (–∞; 1). x 1 x 1  
+) Nếu x > 1, thì f(x) = 4 – x.
Do đó không tồn tại giới hạn của f(x)
Đây là hàm đa thức nên có tập xác định là .
ℝ tại x = 1. Khi đó, hàm số f(x) không
Vậy nó liên tục trên (1; +∞). liên tục tại x = 1. sinx neáu x 0
5.16. Tìm giá trị của tham số m để hàm số f     x  liên tục trên  .  x mneáu x  0 Lời giải:
Tập xác định của hàm số là . ℝ
+) Nếu x > 0, thì f(x) = sin x. Do đó nó liên tục trên (0; +∞).
+) Nếu x < 0, thì f(x) = – x + m, đây là hàm đa thức nên nó liên tục trên (–∞; 0).
Khi đó, hàm số f(x) liên tục trên các khoảng (–∞; 0) và (0; +∞).
Do đó, để hàm số f(x) liên tục trên
ℝ thì f(x) phải liên tục tại x = 0. Điều này xảy ra khi và chỉ khilimf(x) f
 (x)  lim f (x)  lim f (x) f  (0) (1) x 0 x 0 x 0   
Ta l¹i cã lim f (x) lim sin x 0  ; f (0) s  in 0 0  ; x 0 x 0 lim f (x) lim ( x  m) m  ; x 0 x 0 Khi đó, (1) m ⇔
= 0. Vậy m = 0 thì thỏa mãn yêu cầu bài toán.
Document Outline

• Slide 1
• Slide 2
• Slide 3
• Slide 4
• Slide 5
• Slide 6
• Slide 7
• Slide 8
• Slide 9
• Slide 10
• Slide 11
• Slide 12
• Slide 13
• Slide 14
• Slide 15
• Slide 16
• Slide 17
• Slide 18