Giáo án điện tử Toán 11 Bài 2 Chân trời sáng tạo: Đường thẳng vuông góc với mặt phẳng

Bài giảng PowerPoint Toán 11 Bài 2 Chân trời sáng tạo: Đường thẳng vuông góc với mặt phẳng hay nhất, với thiết kế hiện đại, dễ dàng chỉnh sửa giúp Giáo viên có thêm tài liệu tham khảo để soạn Giáo án Toán 11. Mời bạn đọc đón xem!

52 26 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Bài giảng điện tử Toán 11

Môn: Toán 11

Sách: Chân trời sáng tạo

Thông tin:

11 trang 6 tháng trước

Tác giả:

Profile Tin Hin
BÀI 2: ĐƯỜNG THẲNG VUÔNG
GÓC VỚI MẶT PHẲNG
CHÀO MỪNG CÁC EM
ĐẾN VỚI BÀI GIẢNG HÔM NAY
KHỞI ĐỘNG

 !"!#!$
%&'$(
BÀI 2: ĐƯỜNG THẲNG VUÔNG GÓC
VỚI MẶT PHẲNG
NỘI DUNG BÀI HỌC
Đường thẳng vuông góc với mặt phẳng
)
Liên hệ giữa tính song song và tính vuông góc
của đường thẳng và mặt phẳng
*
Phép chiếu vuông góc
+
1. ĐƯỜNG THẲNG VUÔNG GÓC
VỚI MẶT PHẲNG
HĐKP1:
,%-../%0!!/%."12%-$..3456
70!!"
89:75;5%8;%..5"
39<7=> ?8!%-$34560!!"
89
39:%$
%&'$0!!"
Giải
Giải
ĐỊNH NGHĨA
@ $  #!    %&
'$      % 
$A%5BC"
D3-EF8%-03#!
$%&0GH6+9"6%?8!%-
$5270"
Ví dụ 1: SGK – tr.57
Giải
Giải
:$
%&008
%$A%7
%&0"I=8?8
!3A"
D$..8$*J
8..!..%&'$."K>%-$..3456..
G.500..!.9"
HĐKP2:
L..#!8%F8..!."..MN8..38
$.#O#00."IM%-
$J.#O#/."7..#48
%..08.#!%F8..GH6P9"
89L,B/0888%!3A8
39D=>6 8%(Q08?8!
HĐKP2:
Giải
Giải
898%!8%#!/
7G""9"
398%/08
08"
| 1/11
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

BÀI 2: ĐƯỜNG THẲNG VUÔNG
GÓC VỚI MẶT PHẲNG CHÀO MỪNG CÁC EM
ĐẾN VỚI BÀI GIẢNG HÔM NAY KHỞI ĐỘNG
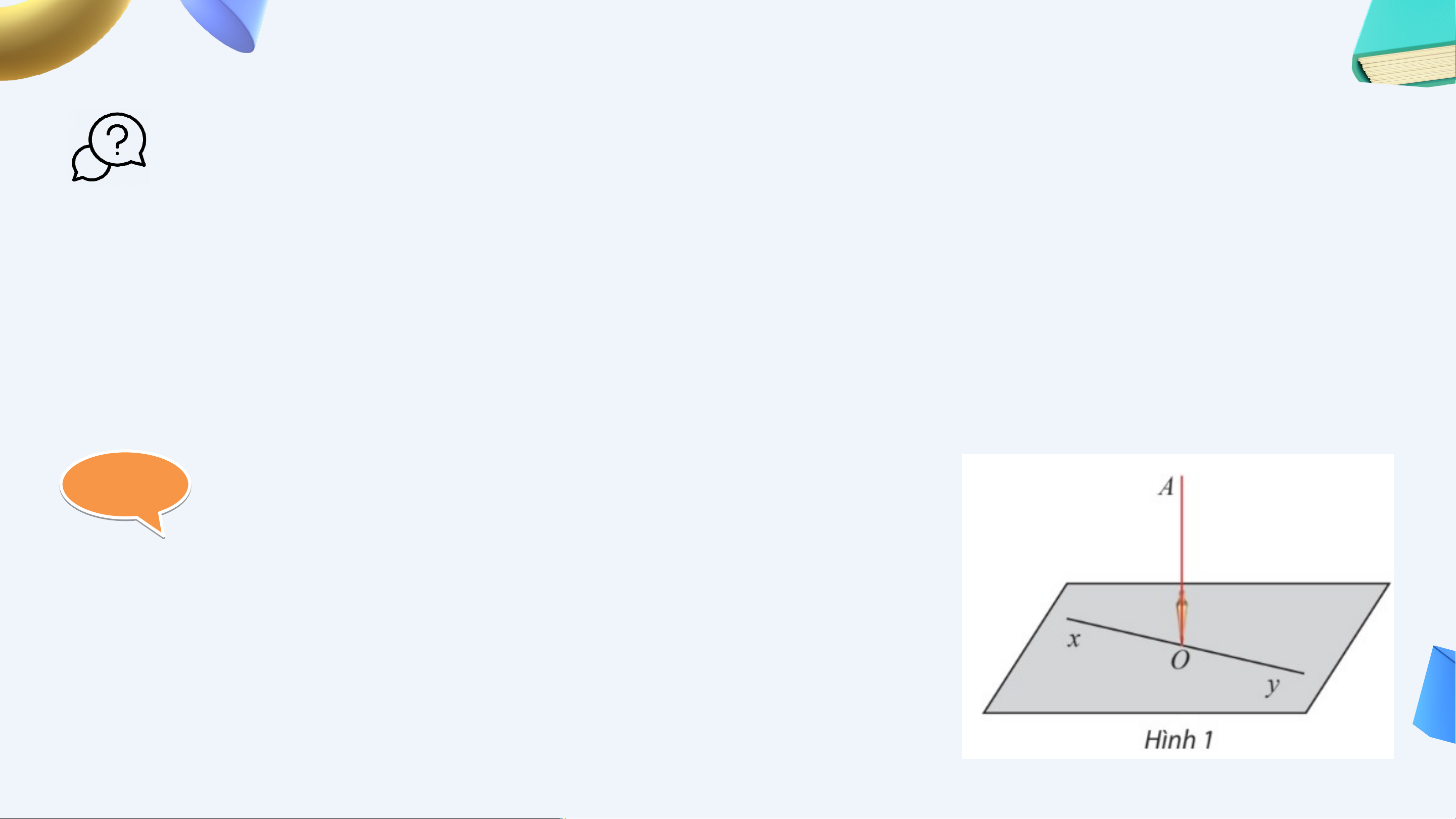
Trong thực tế, người thợ xây dựng thường dùng dây dọi để xác
định đường vuông góc với nền nhà. Thế nào là đường thẳng
vuông góc với mặt phẳng?
BÀI 2: ĐƯỜNG THẲNG VUÔNG GÓC VỚI MẶT PHẲNG NỘI DUNG BÀI HỌC
1 Đường thẳng vuông góc với mặt phẳng
2 Liên hệ giữa tính song song và tính vuông góc
của đường thẳng và mặt phẳng
3 Phép chiếu vuông góc
1. ĐƯỜNG THẲNG VUÔNG GÓC VỚI MẶT PHẲNG HĐK Th P ả 1:
một dây dọi chạm sàn nhà tại điểm . Kẻ một đường thẳng bất kì trên sàn nhà.
a) Dùng êke để kiểm tra xem có vuông góc vớikhông.
b) Nêu nhận xét về góc giữa dây dọi và một đường thẳng bất kì trong sàn nhà. Giải ả a) vuông góc với ,
b) Dây dọi vuông góc với mọi đường thẳng trong mặt phẳng sàn nhà. ĐỊNH NGHĨA
Đường thẳng gọi là vuông góc với mặt
phẳng nếu nó vuông góc với mọi đường
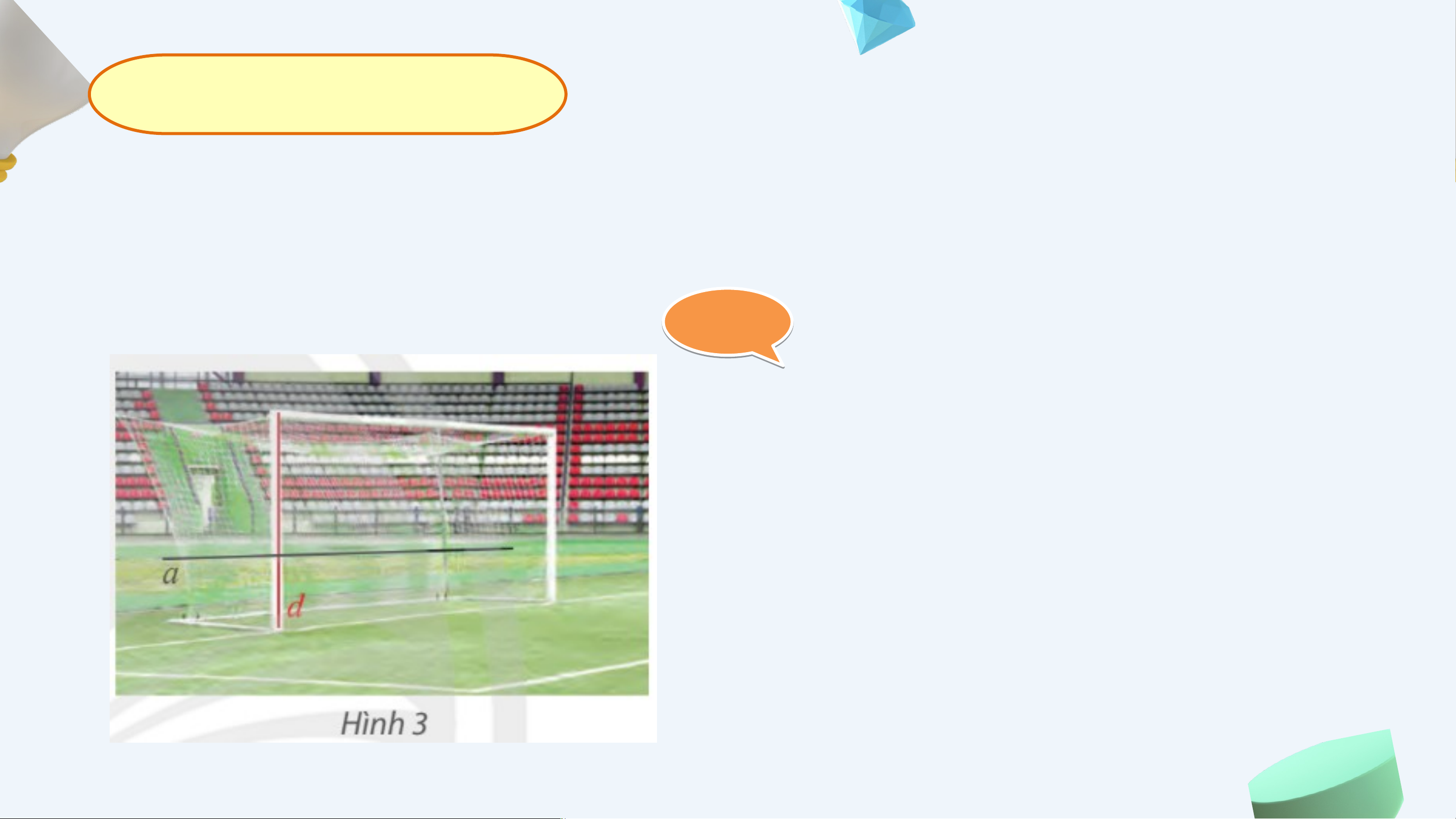
thẳng nằm trong , kí hiệu . Ví dụ 1: S C GK h –o tb r. iế 5 t
7 cột trụ gôn của một sân bóng đá là đường
thẳng vuông góc với mặt sân (Hình 3). Tìm góc giữa và một đường thẳng kẻ trên sân. Giả i i ả
Do đường thẳng vuông góc
với mặt sân suy ra vuông góc
với mọi đường thẳng nằm trên
mặt sân. Vậy ta có góc giữa và bằng . Cho đư
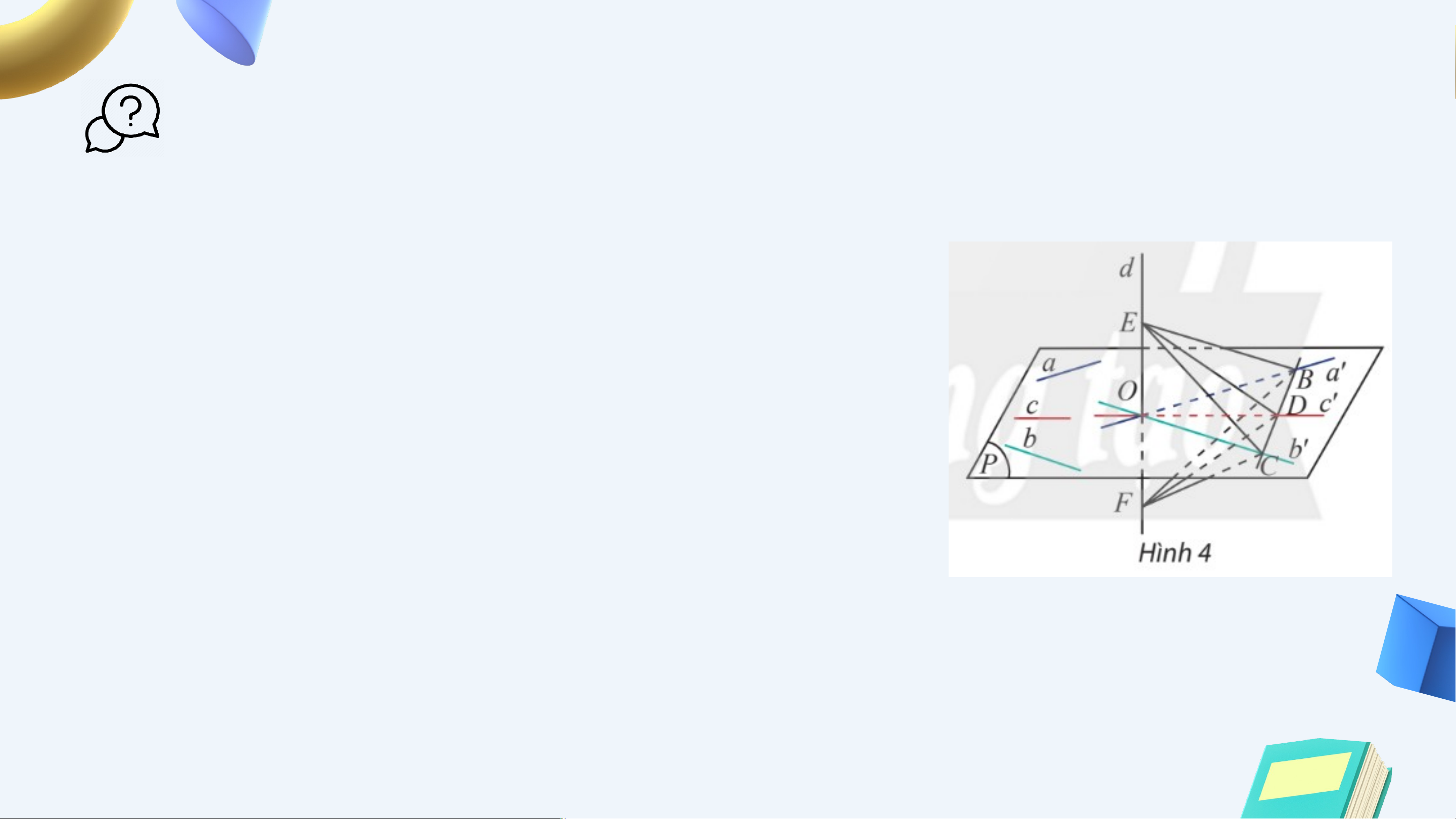
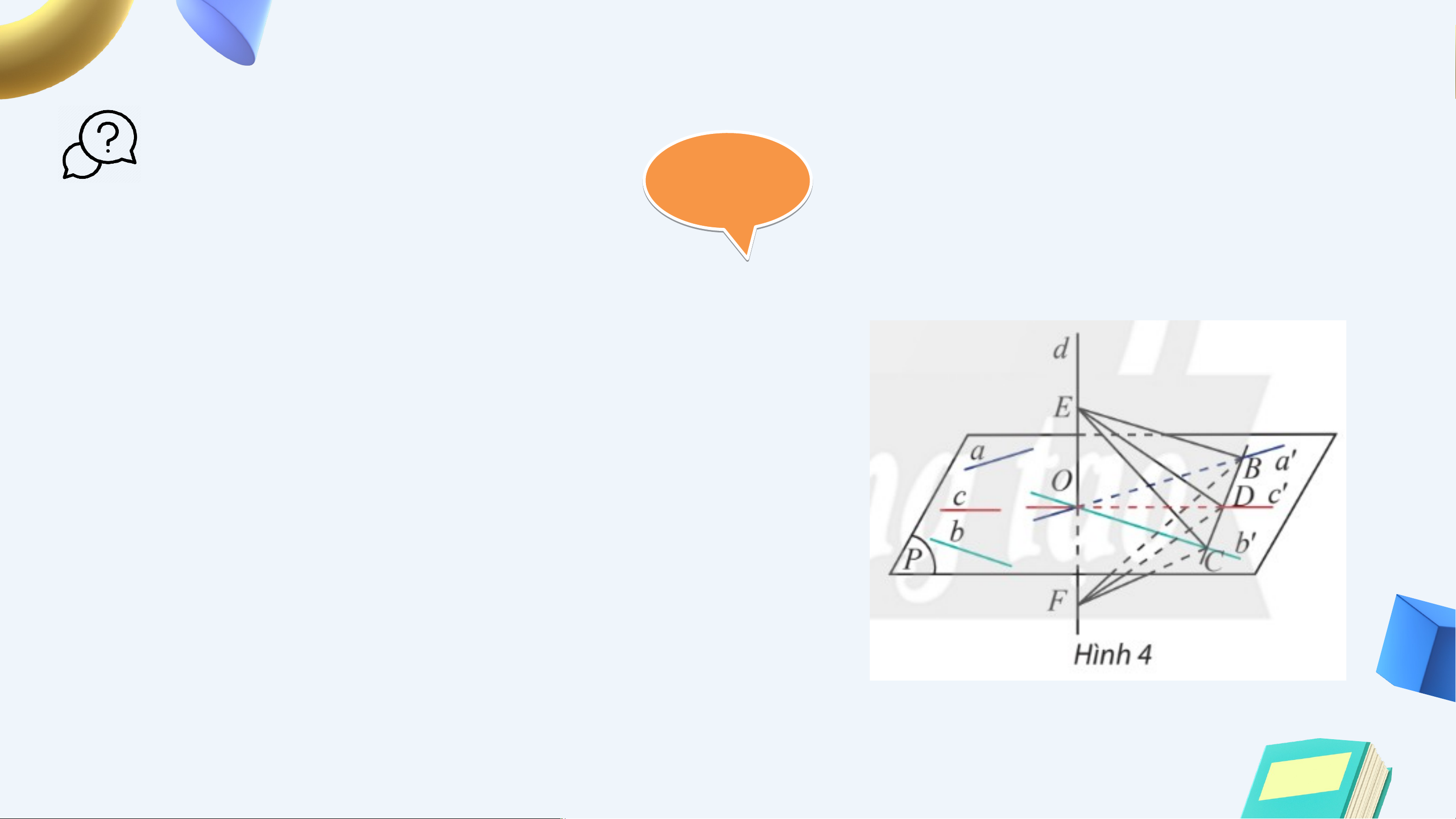
HĐKP2: ờng thẳng vuông góc với hai đường thẳng 2 cắt
nhau và trong mặt phẳng . Xét một đường thẳng bất kì trong
( không song song với và ).
Gọi là giao điểm của và . Trong vẽ qua ba
đường thẳng lần lượt song song với . Vẽ một
đường thẳng cắt lần lượt tại . Trên lấy hai
điểm sao cho là trung điểm của (Hình 4).
a) Giải thích tại sao hai tam giác và bằng nhau
b) Có nhận xét gì về tam giác ? Từ đó suy ra góc giữa và HĐKP2: Giải Gi
a) Tam giác và tam giác có là cạnh chung nên (c.c.c).
b) Tam giác cân tại , suy ra vuông góc với , suy ra .
Document Outline

  • Slide 1
  • Slide 2
  • Slide 3
  • Slide 4
  • Slide 5
  • Slide 6
  • Slide 7
  • Slide 8
  • Slide 9
  • Slide 10
  • Slide 11