Giáo án điện tử Toán 11 Bài 2 Chân trời sáng tạo: Phép tính logarit

Bài giảng PowerPoint Toán 11 Bài 2 Chân trời sáng tạo: Phép tính logarit hay nhất, với thiết kế hiện đại, dễ dàng chỉnh sửa giúp Giáo viên có thêm tài liệu tham khảo để soạn Giáo án Toán 11. Mời bạn đọc đón xem!

65 33 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Bài giảng điện tử Toán 11

Môn: Toán 11

Sách: Chân trời sáng tạo

Thông tin:

30 trang 6 tháng trước

Tác giả:

Profile Tin Hin
Thang Richter được sử dụng để đo độ lớn các trận
động đất. Nếu máy đo địa chấn ghi được biên độ lớn
nhất của một trận động đất là
thì trận động đất đó có độ lớn bằng độ Richter.
Người ta chia các trận động đất thành các mức độ như
sau:
PHÉP TÍNH LÔGARIT
10 μm
M
A
6
1μm = 10 m
M
μm
2,9
10
2,9
3 3,9
10 10
3,0 3, 9
4 4,9
10 10
4,0 4,9
5 5,9
10 10
5, 0 5,9
6 6,9
10 10
6,0 6,9
7 7,9
10 10
7,0 7,9
8
10
8, 0
Bài toán t×m x tho¶:
được gọi là tìm logarit cơ số 2 của 8, của
1/16 hoặc của 5.
Đọc là: “ Lô-ga-rít cơ số 2 của 8’’
VËy tæng qu¸t logarit c¬ sè a cña
b lµ g×?
Tån t¹i khi nµo?
Logarit cơ số a của b có nh÷ng tÝnh
chÊt g×?
1
. 2 8, . 2 , . 2 5.
16
x x x
a b c
1. Khái niệm lôgarit
Độ lớn (theo độ Richter) của một
trận động đất được xác định như
a) Tìm độ lớn theo thang Richter của các
trận động đất có biên độ lớn nhất lần
lượt là
b) Một trận động đất có biên độ lớn nhất
thì độ lớn của nó phải thỏa mãn hệ
thức nào?
M
3,5 4,3
10 ; 100000 ; 100.10m m m
65000A m
M
a)
Biên độ lớn nhất
Độ Richter 3,5 5 6,3
1. Khái niệm lôgarit
b) Độ lớn phải thỏa mãn hệ thức
m
3,5
10
5
100000 10
4,3 6,3
100.10 10
M
10 65000
M
PHÉP TÍNH LÔGARIT
1. Khái niệm lôgarit
Cho hai số . Số thỏa
mãn đẳng thức được gọi là
logarit cơ số a của b. Kí hiệu
Ví dụ. vì
Chó ý: Sè ©m vµ sè 0 kh«ng cã
l«garit
a b
log .
a
b
5
log 25 2
2
5 25.
log .
a
b
a b
, , 1a b R a
Ví dụ 1: Viết các đẳng thức lũy
thừa sau thành đẳng thức
lôgarit:
5
2
0
) 3 243
1
) 10
100
) 3 1
a
b
c
3
log 243 5
10
1
log 2
100
3
log 1 0
Ví dụ : Viết các đẳng thức lũy
thừa sau thành đẳng thức
lôgarit:
3
3
4
) 4 64
1
) 12
1728
) 5 25
a
b
c
4
log 64 3
12
1
log 3
1728
5
log 25 4
log
a
1 = 0,
log
a
a = 1
Chú ý:
Hai công thức cuối cho thấy phép lấy
lôgarit và phép nâng lên lũy thừa là
hai phép toán ngược nhau
Biểu thức chỉ có nghĩa khi
log
a
a
b
a , log ab
log
a
b
0, 1, 0a a b
Ví dụ 2: Tính
3
2
log 5
1
) log
4
) 9
a
b
2
2
log 2 2
3
3
3
log 5
2log 5
2
2
log 5
2
3 3
3 5 25
log
a
1 = 0,
log
a
a = 1
Chú ý:
Ví dụ: Tính
Biểu thức chỉ có nghĩa khi
log
a
a
b
a , log ab
2
a. log 2 2.
5
log 6
b. 25
2
log 7
c. 4
5
1
log
3
1
d.
25
log
a
b
0, 1, 0a a b
Ví dụ: Tính
2
a. log 2 2
5
log 6
b. 25
3
2
2
3
log 2
2
5
5
5
log 6
2 log 6
2
2
log 6
2
5 5
5 6 36
Ví dụ: Tính
2
log 7
c. 4
2
2
2
log 7
2 log 7
2
2
2
log 7
2 2
2 7 7
Ví dụ: Tính
5
1
log
3
1
d.
25
5
5
5
5
1
log
1
1
2 log
3
log
2
3
3
2
2
2
1
log
2
3
1
5 5
5
1
5 3 9
3
HĐTH 1: Tính
5
3
3
1
2
log 4
) log 3
) log 8
1
)
25
a
b
c
1
3
3
1
log 3
3
3
1
2
1
log 3
2
HĐTH 1: Tính
5
log 4
1
)
25
c
5
5
2
log 4
log 4
2
2
5 5
1
4
16
2. Tính lôgarit bằng máy tính cầm tay
Chú ý
a) Lôgarit cơ số 10 được gọi là
lôgarit thập phân. Ta viết:
hay Thay cho
b) Logarit cơ số e còn được gọi là
logarit tự nhiên. Ta viết:
Thay cho
log N
lg N
10
log N
ln N
log
e
N
HĐTH 2 : Sử dụng máy tính cầm tay,
tính giá trị các biểu thức sau (làm tròn
kết quả đến chữ số thập phân thứ sáu)
5
) log 0,5
) log 25
3
) ln
2
a
b
c
0, 430677
1,397940
0, 405465
3. Tính chất của phép tính logarit
HĐKP 2
Cho các số thực dương với
. Bạn Quân đã vẽ sơ đồ và tìm ra
công thức biến đổi biểu thức
Như sau:
, ,a M N
1a
log
a
MN
MN
log log log log
.
a a a a
M N M N
a a a
log
a
MN
a
log log log
a a a
MN M N
a) Giải thích cách làm của bạn Quân.
b) Vẽ sơ đồ tương tự để tìm công
thức biến đổi cho
và
log
a
M
N
log
a
M
3. Tính chất của phép tính logarit
Cho các số thực dương với
, ta có:
3) log log
a a
M M R
1) log ( . ) log log .
a a a
M N M N
2) log ( ) log log .
a a a
M
M N
N
, ,a M N
1a
Chú ý:
Đặc biệt, với dương, , ta có
1
log log
a a
N
N
, ,a M N
1a
1
log log
n
a a
M M n
n
Ví dụ 4: Tính giá trị các biểu thức sau
2 2
2 2
3
3
5
2
) log log 12
3
) log 9 .3
) log 25
a
b
c
Ví dụ 4: Tính giá trị các biểu thức sau
3
2 2 2
2
2
log .12 log 8 log 2
3
3log 2 3.1 3
2 2
2
) log log 12
3
a
Ví dụ 4: Tính giá trị các biểu thức sau
2 2
3
) log 9 .3b
4 2 6
3 3
log 3 .3 log 3 6
3
5
) log 25c
2
3
5
2
log 5
3
Ví dụ : Tính giá trị các biểu thức sau
3 3
2 2
7
4
6
9
) log log 12
4
) log 49 .7
) log 1296
a
b
c
4. Công thức đổi cơ số
Cho các số thực dương với
, ta có:
log
log
log
b
b
a
N
a
N
1
log 1
log
N
a
N
a
N
log .log log
b a b
N Na
1
log log 0
a
a
N N
, ,a b N
1, 1a b
Ví dụ 1. Tính
Ta có
1
4
a. log 2 2.
5 7
log 6 log 8
b. 25 49 .
2
3
2
1 2
2
4
3 1 3
a).log 2 2 log 2 . .log 2 .
2 2 4

5 7 5 7
2 2
5 7 5 7
log 6 log 8 log 6 log 8
2 2
log 6 log 8 log 6 log 8
2 2
2 2
).25 49 (5 ) (7 )
5 7 5 7
6 8 100.
b
Ví dụ 2:
Câu 1. Tính
Câu 2. Cho . Tính theo
3
3
27
b. log .
9
3
log 2
a. 9 .
9 125
2
1 log 4 log 27
2 log 3
c. 3 4 5 .
20
log 5
2
log 20
III. Logarit tự nhiên, logarit thập phân
Logarit cơ số e của x gọi là logarit tự nhiên của
x.
Kí hiệu: lnx.
Logarit cơ số 10 của x gọi là logarit thập phân của
x.
Kí hiệu: logx hoặc lgx.
| 1/30
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

PHÉP TÍNH LÔGARIT
Thang Richter được sử dụng để đo độ lớn các trận
động đất. Nếu máy đo địa chấn ghi được biên độ lớn
nhất của một trận động đất là 1 0 M A  μ m   6 1μm = 10 m 
thì trận động đất đó có độ lớn bằng M độ Richter.
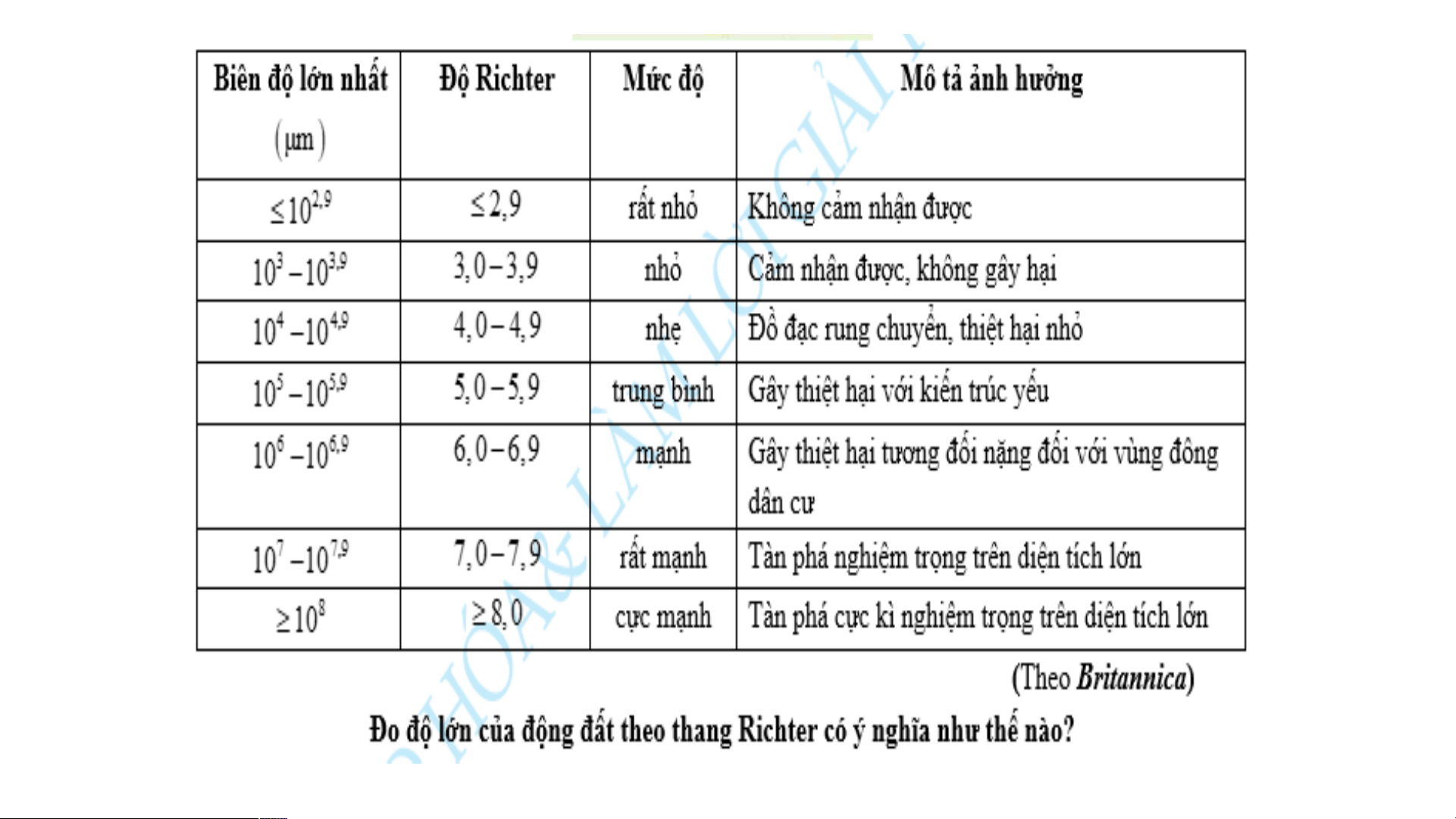
Người ta chia các trận động đất thành các mức độ như sau:  μ  3, 4567,  m 234567, 0 2,9 109 35,9 10 8 10 8, 010 3, 4 567 9467,9 10 10,9 10 10 10
Bài toán t×m x tho¶: x x 1 . 2 8  , . 2  , . 2x a b c 5  . 16
được gọi là tìm logarit cơ số 2 của 8, của 1/16 hoặc của 5.
Đọc là: “ Lô-ga-rít cơ số 2 của 8’’
VËy tæng qu¸t logarit c¬ sè a cña b lµ g×? Tån t¹i khi nµo?
Logarit cơ số a của b có nh÷ng tÝnh chÊt g×?
1. Khái niệm lôgarit Độ lớn
M (theo độ Richter) của một
trận động đất được xác định như
a) Tìm độ lớn theo thang Richter của các
trận động đất có biên độ lớn nhất lần lượt là 3,5 4,3
10 m ; 100000 m ; 100.10 m
b) Một trận động đất có biên độ lớn A nh 6  ất 50 00m M
thì độ lớn của nó phải thỏa mãn hệ thức nào?
1. Khái niệm lôgarit a)
Biên độ lớn nhấtm 3,5 10 5 100000 1  0 4,3 6,3 100.10 1  0 Độ Richter 3,5 5 6,3 b) Độ lớn
M phải thỏa mãn hệ thức 10M 65  000 PHÉP TÍNH LÔGARIT
1. Khái niệm lôgarit Cho hai số . S
a , b R, a 1    ố thỏa mãn đẳng thức a đbược gọi là
logarit cơ số a của b. Kí hiệu log . b a log b a     . b a Ví dụ. l og 25 2  vì 2 5 25.  5
Chó ý: Sè ©m vµ sè 0 kh«ng cã l«garit
Ví dụ 1: Viết các đẳng thức lũy
thừa sau thành đẳng thức lôgarit:5 a) 3 2  43  log 243 5 3  1  1 2 b) 10   log  2 100 10 100 c)  30 1   log 1 0  3
Ví dụ : Viết các đẳng thức lũy
thừa sau thành đẳng thức lôgarit:3 a) 4 64   log 64 3 4  1  1 3 b) 12   log  3 1728 12 1728 c)  54 2  5  log 25 4  5 Chú ý: Biểu thức l o g
b chỉ có nghĩa khi a a  0, a 1  , b  0  log 1 = 0, a  log a = 1 a log b   a a b, log a   a
Hai công thức cuối cho thấy phép lấy
lôgarit và phép nâng lên lũy thừa là
hai phép toán ngược nhau Ví dụ 2: Tính 1 a) log  2 2 l  og 2  2 4 2 log log3 5 3 5 b) 9  2  3  2log3 5 3   2 log3 5  3  2 5  2  5 Chú ý: Biểu thức l o g
b chỉ có nghĩa khi a a  0, a 1  , b  0  log 1 = 0, a  log a = 1 a log b   a a b, log a   a Ví dụ: Tính log 6 a. log 2 2. 5 b. 25 2 1 log5 log 3  1  2 7 c. 4 d.  25   Ví dụ: Tính 3 3 a. log 2 2 2 l  og 2 2 2 2 log5 6 b. 25  2  5 log5 6 2 log5 6 5   2 log5 6  5  2 6  3  6 Ví dụ: Tính log2 7 c. 4  2  2 log2 7 2 log2 7 2   2 2 log2 7  2    7  7  Ví dụ: Tính 1 log5 3  1 d.   25    1 log5  1 1  3  2 log  1     2  5 log  5 5  3   3 5    2  5   2 1  2  log5   1  2 3  5  3  9     3     HĐTH 1: Tính 1 1 3 a) log 3 3 l  og 3 3 3 3  3  1 b) log 8 log    3 1 1  2  2 2  log5 4  1 c)   25    HĐTH 1: Tính log5 4  1 c)   25     2   5 log5 4  2 log5 4  5   1 2 4  16
2. Tính lôgarit bằng máy tính cầm tay Chú ý
a) Lôgarit cơ số 10 được gọi là
lôgarit thập phân. Ta viết: log N hay lg
N Thay cho log N 10
b) Logarit cơ số e còn được gọi là
logarit tự nhiên. Ta viết: ln N Thay cho log N e HĐTH 2
: Sử dụng máy tính cầm tay,
tính giá trị các biểu thức sau (làm tròn
kết quả đến chữ số thập phân thứ sáu)
a) log 0,5  0, 430677 5 b) log 25 1  , 397940 3 c) ln 2 0  , 405465
3. Tính chất của phép tính logarit HĐKP 2 Cho các số thực dương a, M , N với a  .
1 Bạn Quân đã vẽ sơ đồ và tìm ra
công thức biến đổi biểu thức log MN a  
Như sau: log M log N log M log a . a a a N a a a   MN loga MN a  log MN l
 og M  log N a a a
a) Giải thích cách làm của bạn Quân.
b) Vẽ sơ đồ tương tự để tìm công
thức biến đổi cho M l og a N và log Ma   
3. Tính chất của phép tính logarit
Cho các số thực dương a , M , N với a 1 , ta có: 1) log (M .N) l
 og M  log N. a a a M 2) log ( ) l
 og M  log N. a a a N 3) log M    log M   R a a   Chú ý:
Đặc biệt, với a , M , N dương, a  1 , ta có 1  log  log N a a N 1
 log n M  log M na a    n
Ví dụ 4: Tính giá trị các biểu thức sau 2 a) log  log 12 2 2 3 b) log  2 2 9 .3 3  3 c) log 25 5
Ví dụ 4: Tính giá trị các biểu thức sau 2 a) log  log 12 2 2 3  2  3 l  og .12 l  og 8 l  og 2 2   2 2  3  3  log 2 3  .1 3 2 
Ví dụ 4: Tính giá trị các biểu thức sau b) log  2 2 9 .3 3  l  og  4 2 3 .3  6 l  og 3 6 3 3  3 c) log 25 5 2 2 3 log 5 5 3
Ví dụ : Tính giá trị các biểu thức sau 9 a) log  log 12 3 3 4 b) log  2 2 49 .7 7  4 c) log 1296 6
4. Công thức đổi cơ số
Cho các số thực dương a , b, N với a 1, b 1 , ta có: 1 log N N a    1 log a N log N log b N log . a log N l  og N a  log a b a b b 1 log     N log N  0 aa
Ví dụ 1. Tính a. log 2 2. log 6 log 8 5 7 b. 25  49 . 1 4 3 Ta có 3  1  3 2 a).log 2 2 l  og    2 . .log 2 . 2 1   2 2 2   2  4 4 log5 6 log7 8 2 log5 6 2 log7 8 b).25  49 (  5 )  (7 )  2 2 2log5 6 2log7 8 log5 6 log7 8 5   7 5   7  2 2 6   8 1  00. Ví dụ 2: Câu 1. Tính log 2 27 3 a. 9 . b. log . 3 3 9 1log9 4 2 log2 3 lo 1 g 25 27 c. 3  4  5 . Câu 2. Cho  l  o g 20  2 . Tính l og 5 theo 20
III. Logarit tự nhiên, logarit thập phân
 Logarit cơ số e của x gọi là logarit tự nhiên của x. Kí hiệu: lnx.
 Logarit cơ số 10 của x gọi là logarit thập phân của x.
Kí hiệu: logx hoặc lgx.
Document Outline

  • Slide 1
  • Slide 2
  • Slide 3
  • 1. Khái niệm lôgarit
  • a)
  • Slide 6
  • Slide 7
  • Slide 8
  • Slide 9
  • Ví dụ 2: Tính
  • Slide 11
  • Slide 12
  • Slide 13
  • Slide 14
  • Slide 15
  • Slide 16
  • Slide 17
  • Slide 18
  • Slide 19
  • Slide 20
  • Slide 21
  • Chú ý: Đặc biệt, với dương, , ta có
  • Ví dụ 4: Tính giá trị các biểu thức sau
  • Ví dụ 4: Tính giá trị các biểu thức sau
  • Ví dụ 4: Tính giá trị các biểu thức sau
  • Ví dụ : Tính giá trị các biểu thức sau
  • Slide 27
  • Slide 28
  • Slide 29
  • Slide 30