















Preview text:
BÀI 21. PHƯƠNG TRÌNH, BẤT PHƯƠNG TRÌNH MŨ VÀ LÔGARIT CHÀO MỪNG TẤT CẢ CÁC EM
ĐẾN VỚI TIẾT HỌC! KHỞI ĐỘNG
Giả sử giá trị còn lại (tính theo triệu đồng) của một chiếc ô tô
sau năm sử dụng được mô hình hóa bằng công thức:
Hỏi nếu theo mô hình này, sau bao nhiêu năm sử dụng thì giá trị
của chiếc ô tô đó còn lại không quá triệu đồng? (Làm tròn kết
quả đến hàng đơn vị).
CHƯƠNG VI: HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
BÀI 21. PHƯƠNG TRÌNH, BẤT PHƯƠNG TRÌNH MŨ VÀ LÔGARIT NỘI DUNG BÀI HỌC 01 Phương trình mũ
02 Phương trình lôgarit
03 Bất phương trình mũ
04 Bất phương trình lôgarit 01 PHƯƠNG TRÌNH MŨ 1 HĐ H 1
Xét phương trình: 2𝑥 +1= 4 1 a) Khi viết
4 thành luỹ thừa của thì phương trình trên trở thành phương trình nào?
b) So sánh số mũ của ở hai vế của phương trình nhận được ở câu a để tìm . Giải: a) b) Ta có: KẾT LUẬN
Phương trình mũ cơ bản có dạng (với )
- Nếu thì phương trình có nghiệm duy nhất .
- Nếu thì phương trình vô nghiệm. Ch C ú h ú ý
Phương pháp giải phương trình mũ bằng cách đưa về cùng cơ số: Nếu thì 1
Ví dụ 1: Giải phương trình3𝑥+1= 31−2𝑥 Giải 1
Đưa vế phải về cơ số 3, ta có 31−2𝑥 =32𝑥−1
Từ đó phương trình trở thành
Vậy phương đã cho có nghiệm duy nhất
Ví dụ 2: Giải phương trình Giải:
Lấy lôgarit thập phân hai vế của phương trình ta được hay
Vậy phương trình đã cho có nghiệm duy nhất
Giải các phương trình sau Luyện tập 1 1
𝑎 ¿ 23𝑥 −1=
; 𝑏 ¿ 2𝑒2𝑥 =5 2𝑥+1 Giải
Vậy phương trình có nghiệm
Vậy phương trình có nghiệm 02 PHƯƠNG TRÌNH LÔGARIT HĐ H Đ 2 Xét phương trình:
Từ phương trình trên, hãy tính
Từ kết quả ở câu a và sử dụng định nghĩa lôgarit, hãy tìm . Giải: KẾT LUẬN
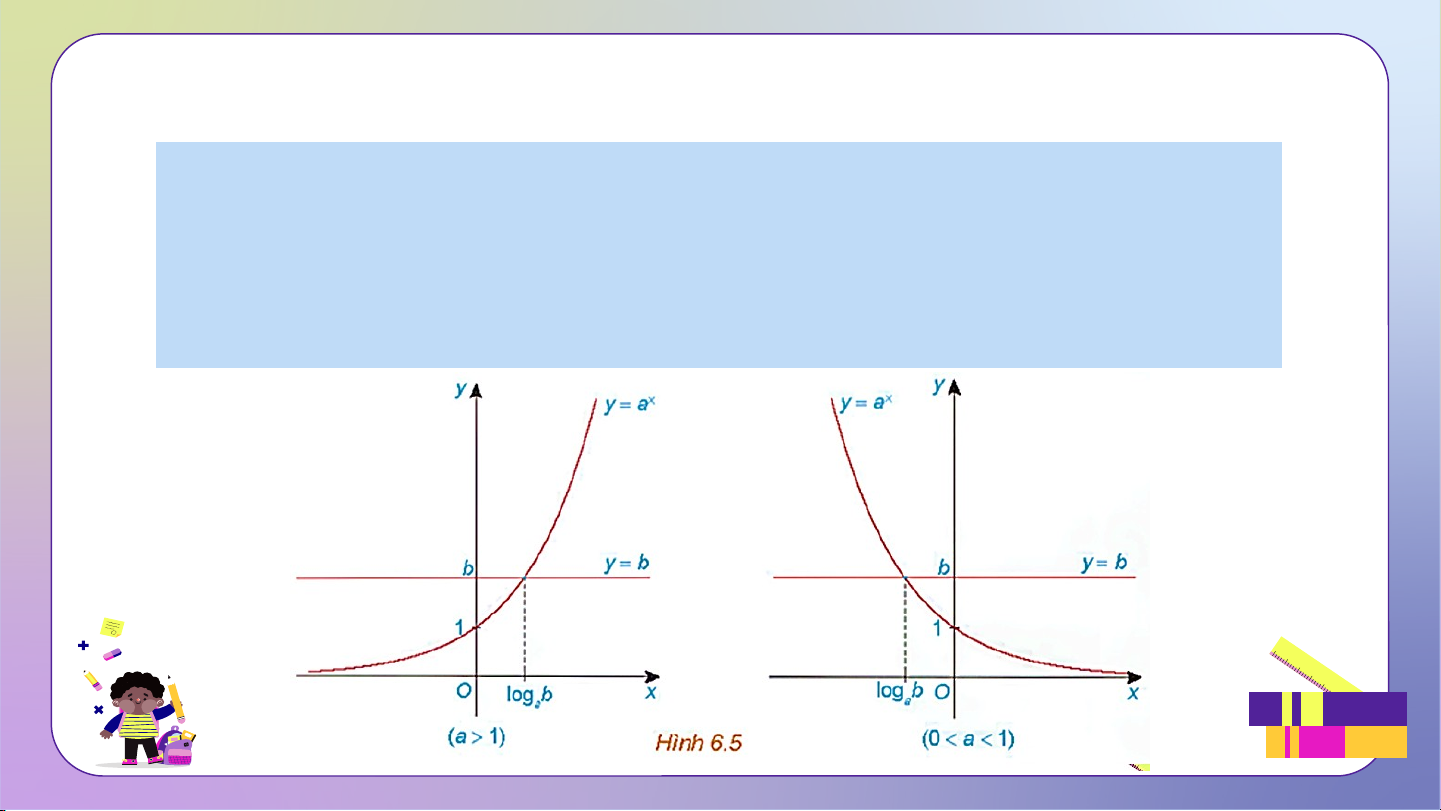
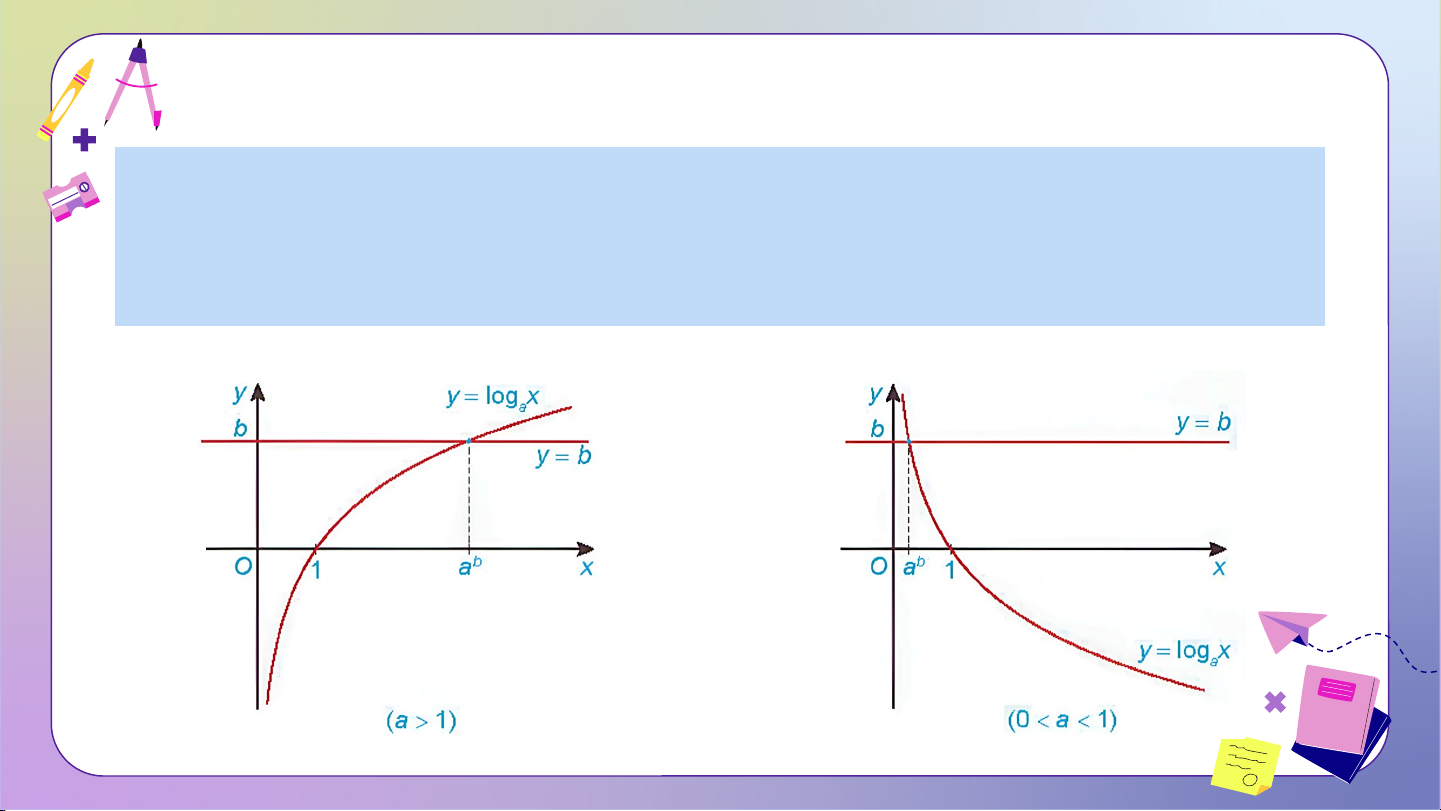
Phương trình lôgarit cơ bản có dạng .
Phương trình lôgarit cơ bản có nghiệm duy nhất . Đến giờ câu cá rồi. Các em hãy giúp ông nhé
Câu 1. Nghiệm của phương trình là A. x = 1 C. x = – 2 B. x = 2 D. x = – 1 Sai mất Sai mất Sai mất A B rồi Crồi Drồi
Câu 2. Nghiệm của phương trình là A. x = 18 C. x = 39 B. x = 25 D. x = 3 S Sai mất Sai mất A ai mất rồi B Crồi Drồi
Bài 6.21 (SGK – tr.24)
Giải các phương trình sau: a) b) c) d) Giải: d) Điều kiện: .
Phương trình đã cho tương đương với hoặc .
Kết hợp với điều kiện, phương trình có nghiệm duy nhất .
Bài 6.22 (SGK – tr.24)
Giải các bất phương trình sau: a 2
¿ 0 , 1 2− 𝑥 >0 , 1 4+ 2 𝑥
⇔ 2− 𝑥 < 4+ 2 𝑥 ⇔ 𝑥> − 3 3 3 1 3
b¿2⋅52𝑥+1≤3
⇔ 2 𝑥 +1 ≤ log − 1 5
⇔ 52𝑥+1 ≤
2 ⇔ 𝑥 ≤ 2 ( log5 2 ) 2
c¿log3(𝑥+7)≥−1 Điều kiện: Ta có:
d¿log0,5(𝑥+7)≥log0,5(2𝑥−1) Điều kiện: Ta có: . VẬN DỤNG
Bài 6.23 (SGK – tr.24)
Bác Minh gửi tiết kiệm triệu đồng ở một ngân hàng với lãi suất không
đổi một năm theo thể thức lãi kép kì hạn tháng. Tổng số tiền bác
Minh thu được (cả vốn lẫn lãi) sau năm là: (triệu đồng).
Tính thời gian tối thiểu gửi tiết kiệm để bác Minh thu được ít nhất
triệu đồng (cả vốn lẫn lãi). CẢM ƠN CÁC EM
ĐÃ THEO DÕI TIẾT HỌC!
Document Outline
- Slide 1
- Slide 2
- KHỞI ĐỘNG
- Slide 4
- 04
- 01
- HĐ 1
- KẾT LUẬN
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- 02
- HĐ 2
- KẾT LUẬN
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- VẬN DỤNG
- Slide 23
- Slide 24




