Giáo án điện tử Toán 11 Bài 30 Kết nối tri thức: Công thức nhân xác suất cho hai biến cố độc lập

CHÀO MỪNG TẤT CẢ CÁC EM
ĐẾN VỚI TIẾT HỌC! KHỞI ĐỘNG
Tại vòng chung kết của một đại hội thể thao, vận động viên An thi đấu môn Bắn
súng, vận động viên Bình thi đấu môn Bơi lội.
Biết rằng xác suất giành huy chương của vận động viên An và vận động viên Bình
tương ứng là 0,8 và 0,9. Hỏi xác suất để cả hai vận động viên đạt huy chương là bao nhiêu?
CHƯƠNG VIII. CÁC QUY TẮC TÍNH XÁC SUẤT
BÀI 30: CÔNG THỨC NHÂN XÁC
SUẤT CHO HAI BIẾN CỐ ĐỘC LẬP NỘI DUNG BÀI HỌC
Công thức nhân xác suất cho hai biến cố độc lập 1 Vận dụng 2
1. Công thức nhân xác suất
cho hai biến cố độc lập H Đ 1
Có hai hộp đựng các quả bóng có cùng kích thước và khối
lượng. Hộp I có 6 quả màu trắng và 4 quả màu đen. Hộp II có 1 quả
màu trắng và 7 quả màu đen. Bạn Long lấy ngẫu nhiên một quả bóng
từ hộp I, bạn Hải lấy ngẫu nhiên một quả bóng từ hộp II. Xét các biến cố sau:
: “Bạn Long lấy được quả bóng màu trắng”;
: “Bạn Hải lấy được quả bóng màu đen”. a) Tính và b) So sánh và Giải Tính Vậy KHÁI NIỆM
Nếu hai biến cố và độc lập với nhau thì
Công thức này gọi là công thức nhân xác suất cho hai biến cố độc lập.
Hai biến cố và trong HĐ1 độc lập hay không độc lập? Tại sao ? Trả lời:
Nếu A xảy ra, tức là bạn Long lấy được quả bóng màu trắng từ hộp I, thì
Nếu A không xảy ra, tức là bạn Long lấy được quả bóng màu đen từ hộp I, thì
Tương tự, biến cố B xảy ra hay không ta đều có
Vậy hai biến cố A và B độc lập.
Chú ý. Với hai biến cố và , nếu thì và không độc lập.
Ví dụ 1. Trở lại tình huống mở đầu. Gọi là biến cố “Vận động viên An đạt huy chương”;
là biến cố “Vận động viên Bình đạt huy chương”.
a) Giải thích tại sao hai biến cố và là độc lập.
b) Tính xác suất để cả hai vận động viên đạt huy chương.
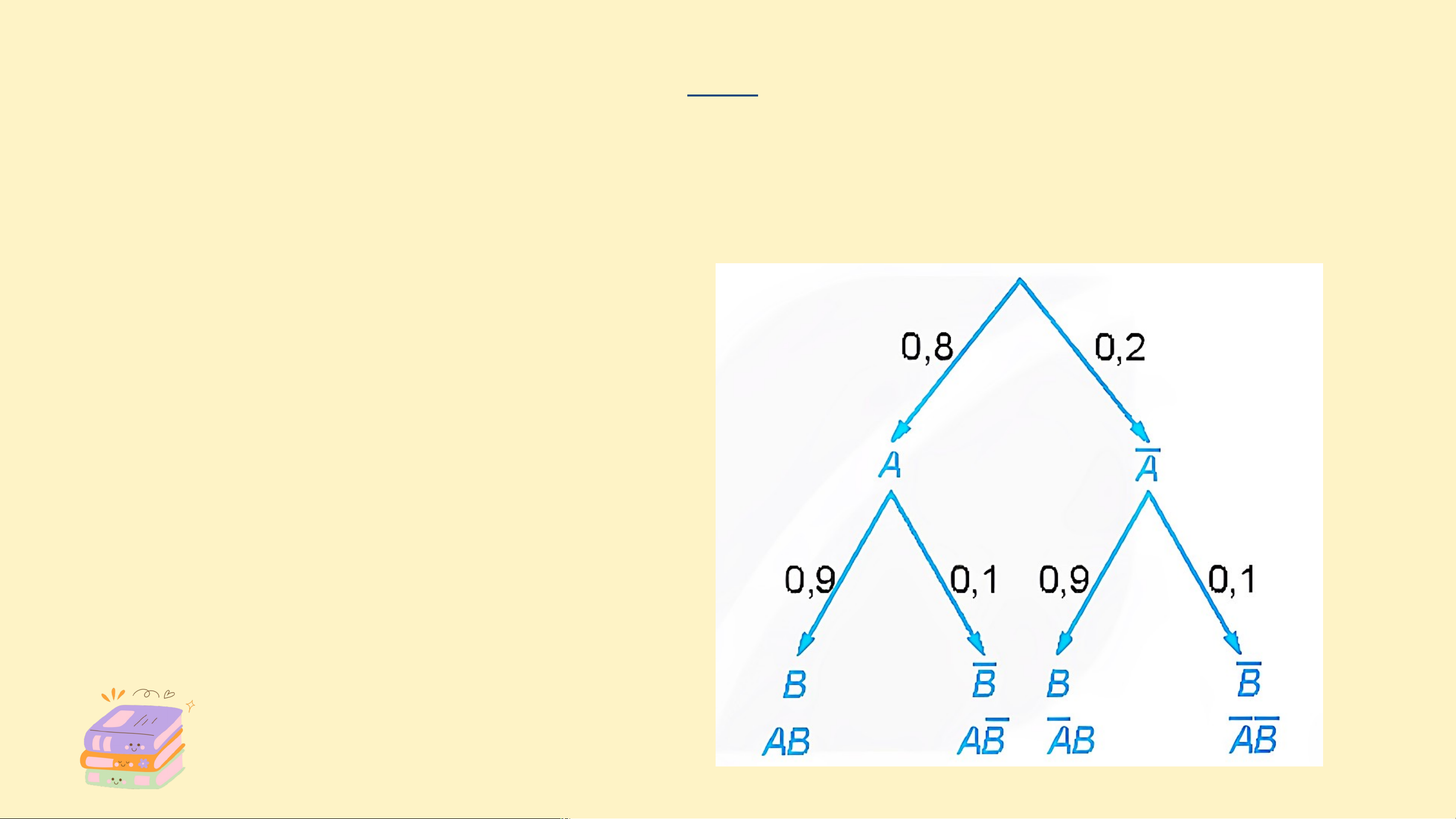
c) Sử dụng sơ đồ hình cây, tính xác suất để:
- Cả hai vận động viên không đạt huy chương;
- Vận động viên An đạt huy chương, vận động viên Bình không đạt huy chương;
- Vận động viên An không đạt huy chương, vận động viên Bình đạt huy chương. Giải
a) Vì hai vận động viên An và Bình thi đấu hai môn thể thao khác nhau nên hai biến cố và là độc lập.
b) Ta phải tính . Theo công thức nhân xác suất, ta có: Giải
c) Ta phải tính . Ta dùng sơ đồ hình cây để mô tả như sau:
Theo sơ đồ hình cây, ta có: Luyện tập 1
Các học sinh lớp 11D làm thí nghiệm gieo hai loại hạt giống A và B. Xác
suất để hai loại hạt giống A và B nảy mầm tương ứng là 0,92 và 0,88.
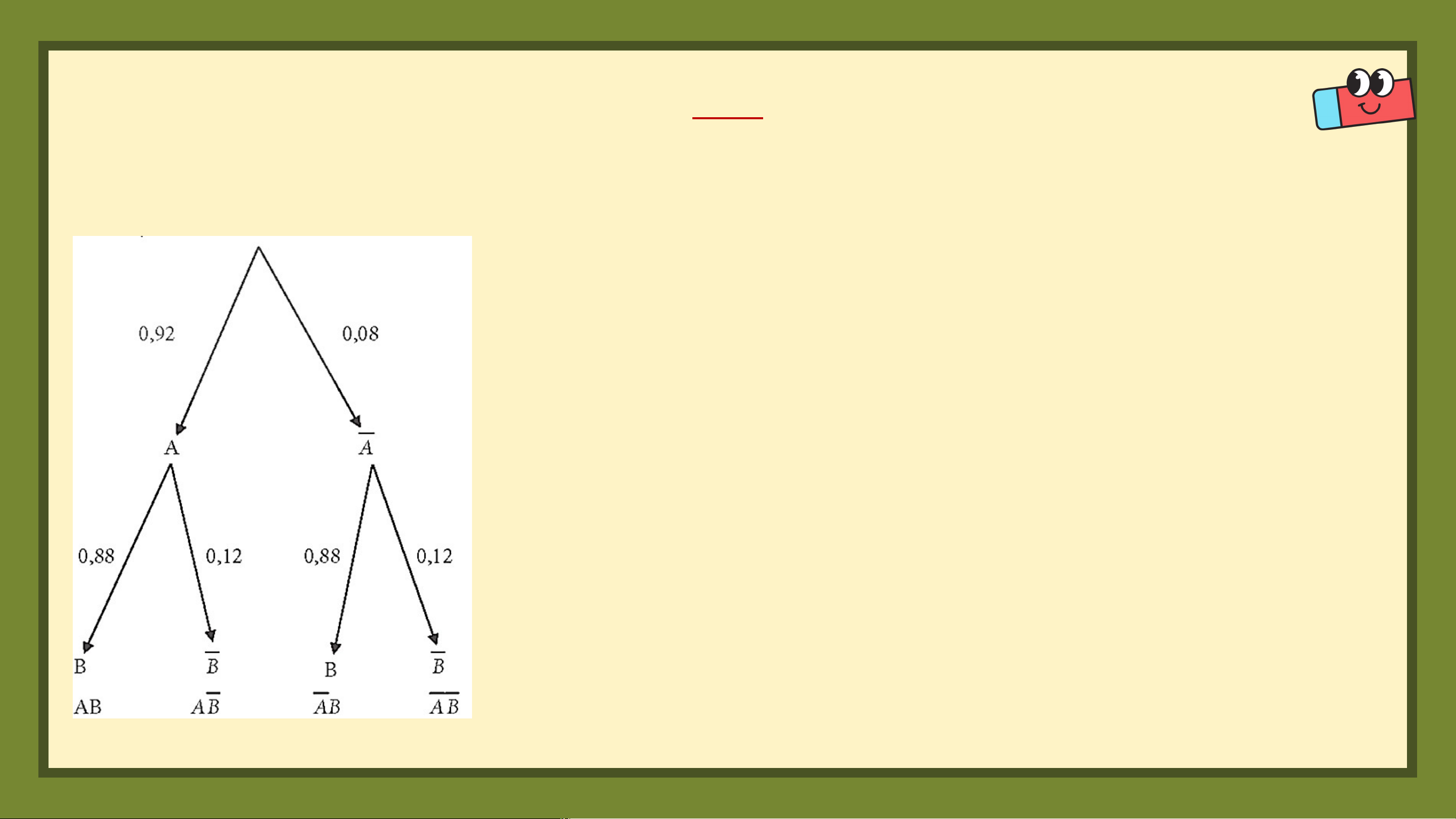
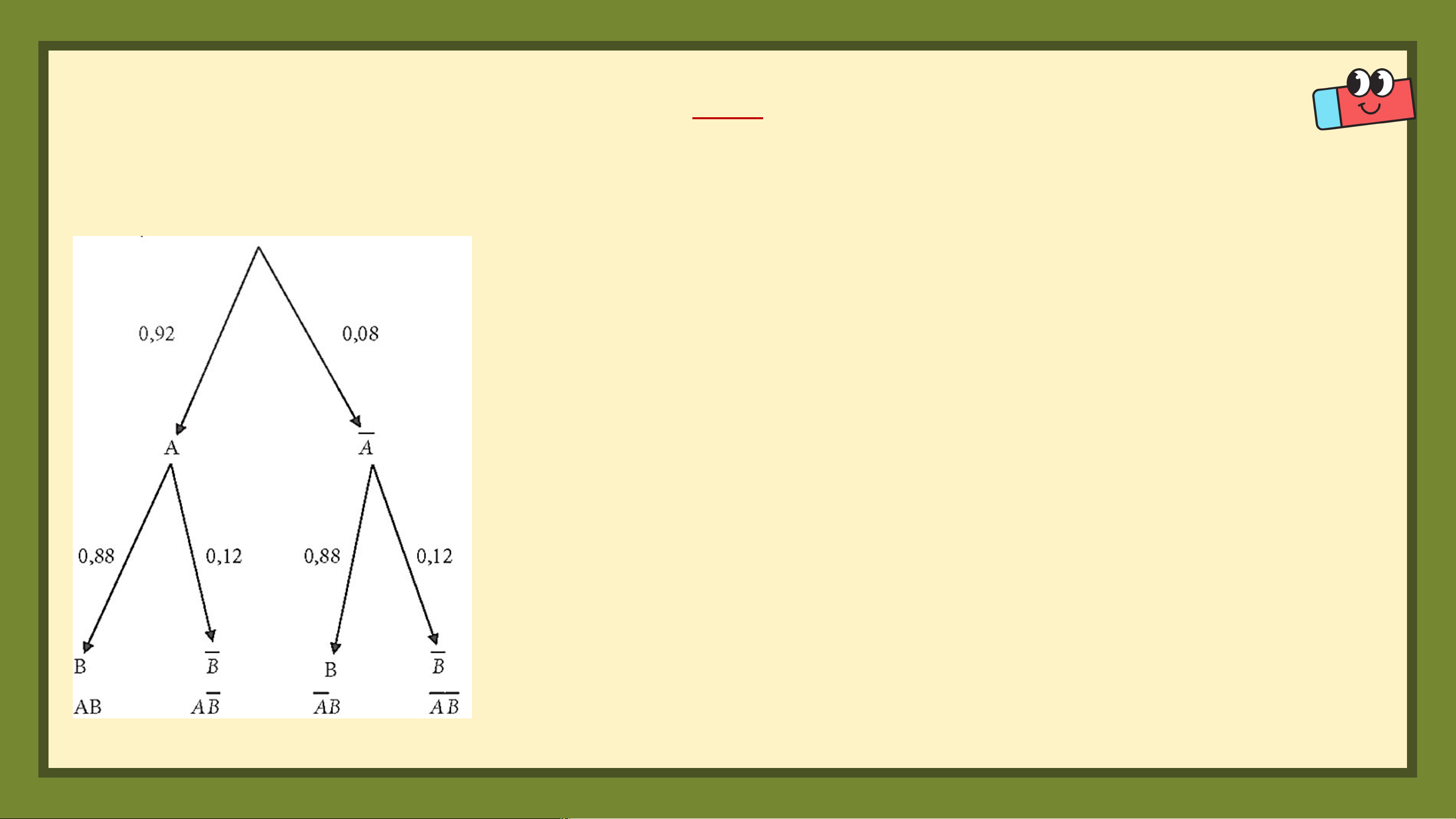
Giả sử việc nảy mầm của hạt A và hạt B là độc lập với nhau. Dùng sơ đồ
hình cây, tính xác suất để:
a) Hạt giống A nảy mầm còn hạt giống B không nảy mầm;
b) Hạt giống A không nảy mầm còn hạt giống B nảy mầm;
c) Ít nhất có một trong hai loại hạt giống nảy mầm. Giải
Gọi biến cố : “Hạt A nảy mầm”; : “Hạt B nảy mầm”. .
Hai biến cố và độc lập.
a) Biến cố“Hạt A nảy mầm, hạt B không nảy mầm” là biến cố
b) Biến cố: “Hạt A không nảy mầm còn hạt giống B
nảy mầm” là biến cố Giải
Gọi biến cố : “Hạt A nảy mầm”; : “Hạt B nảy mầm”.
c) Biến cố: “Có ít nhất một trong hai hạt nảy mầm” là biến cố . Vậy 2. VẬN DỤNG
Ví dụ 2. Số liệu thống kê tại một vùng cho thấy trong các vụ tai nạn ô tô có 0,37% người
tử vong; 29% người không thắt dây an toàn và 0,28% người không thắt dây an toàn và tử
vong. Chứng tỏ rằng việc không thắt dây an toàn khi lái xe và nguy cơ tử vong khi gặp tai
nạn có liên quan với nhau. Giải
Chọn ngẫu nhiên một người đã bị tai nạn ô tô.
Gọi là biến cố “Người đó đã tử vong”;
là biến cố “Người đó đã không thắt dây an toàn”.
Khi đó, là biến cố “Người đó không thắt dây an toàn và đã tử vong”. Ta có suy ra .
Ví dụ 2. Số liệu thống kê tại một vùng cho thấy trong các vụ tai nạn ô tô có 0,37%
người tử vong; 29% người không thắt dây an toàn và 0,28% người không thắt dây
an toàn và tử vong. Chứng tỏ rằng việc không thắt dây an toàn khi lái xe và nguy
cơ tử vong khi gặp tai nạn có liên quan với nhau. Giải Mặt khác
Vì nên hai biến cố và không độc lập.
Vậy việc không thắt dây an toàn khi lái xe có liên quan tới nguy cơ tử vong khi gặp tai nạn. Luyện tập 2
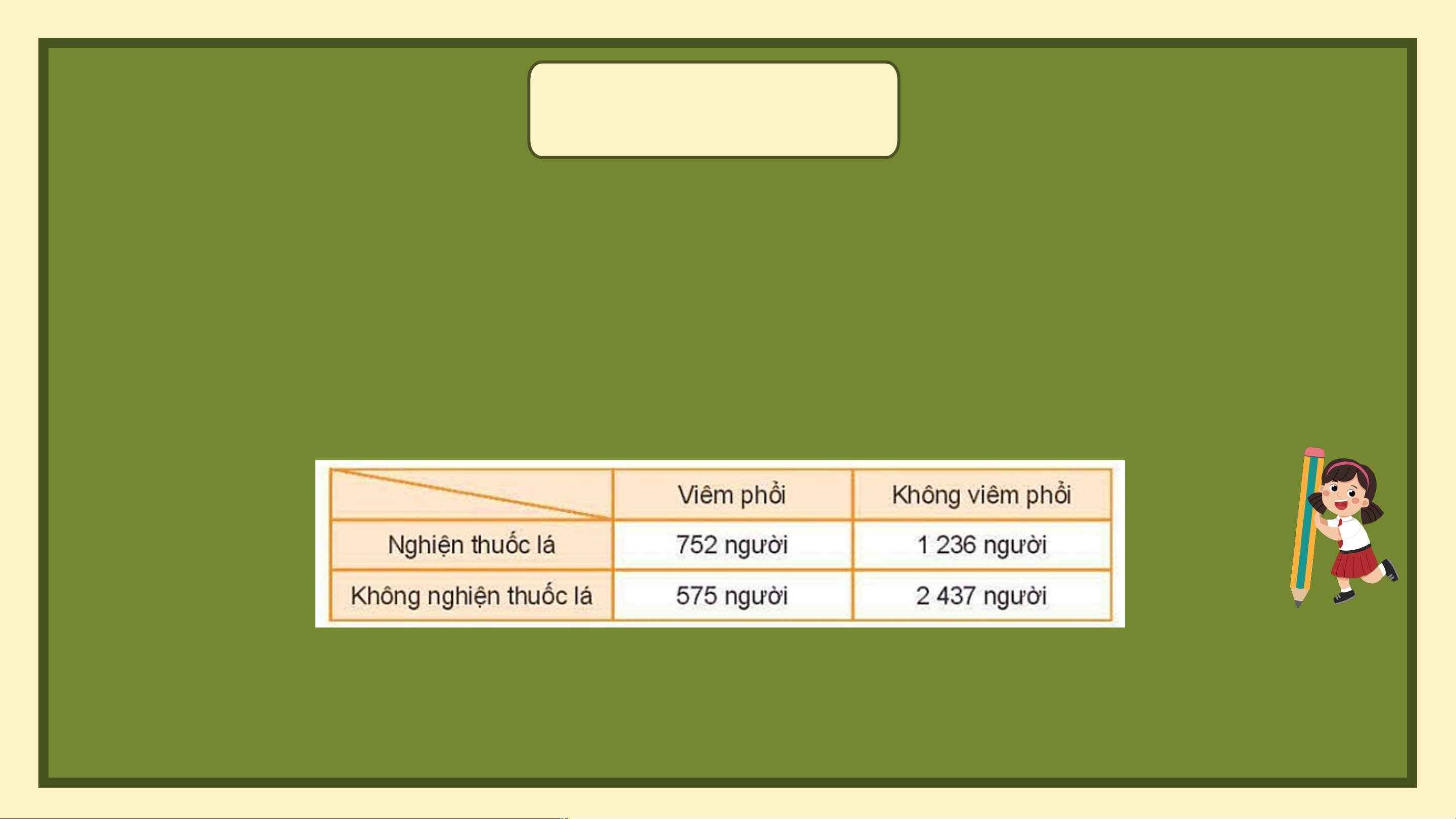
Để nghiên cứu mối liên quan giữa thói quen hút thuốc lá với bệnh viêm phổi, nhà
nghiên cứu chọn một nhóm 5 000 người đàn ông. Với mỗi người trong nhóm, nhà
nghiên cứu kiểm tra xem họ có nghiện thuốc lá và có bị viêm phổi hay không. Kết quả
được thống kê trong bảng sau:
Từ bảng thống kê trên, hãy chứng tỏ rằng việc nghiện thuốc lá và mắc bệnh
viêm phổi có liên quan với nhau. Giải
Chọn ngẫu nhiên một người trong nhóm người đang xét. Xét các biến cố sau:
“Người đó nghiện thuốc lá”; “Người đó mắc bệnh viêm phổi”.
Khi đó là biến cố: “Người đó nghiện thuốc là và mắc bệnh viêm phổi”.
Số người nghiện thuốc lá là:
Số người mắc bệnh viêm phổi là:
Số người nghiện thuốc lá và mắc bệnh viêm phổi là Ta có
Vậy hai biến cố và không độc lập.
Do đó ta kết luận việc nghiện thuốc lá và mắc bệnh viêm phổi có liên quan với nhau. LUYỆN TẬP THU HOẠCH TRỨNG GÀ Nh N ữ h ng ữ ng ch c ú h gà gà mái á của ủ chún ú g n g ta ta đã đ ã đẻ đ ẻ rấ r t ấ nh n iề h u iề trứn ứ g n . g Bạ B n ạ hã h y ã giúp gi úp mìn m h ìn thu thu ho h ạ o ch ạ ch số số trứn ứ g n g đó đ ó bằn bằ g n g cách cá ch trả ả lời các cá câu câ u hỏi hỏ nh n é. h Kh K i h bạn b ạn trả l tr ờ ả l i đú đ n ú g n g là à trứn tr g ứn đ g ã đ ã vào v g ào iỏ g củ iỏ a m củ ình a m r ình ồi ồ đấ đ y ấ . y Nà N o à o bắ b t đầ ắ u t đầ th u ôi th ! ôi Câ C u 1. 1 Hai a bạ b n ạ n Hạ H nh n h và và Hà H cùn ù g n g chơ h i tr t ò ò chơ h i bắ b n ắ cung n g một mộ các á h h độ đ c lập. p .Mỗ M i bạ b n ạ n chỉ h bắ b n n một mộ lần ầ . .Xác Xá suấ u t ấ để ể bạ b n n Hạn ạ h n và à bạ b n n Hà à bắ b n n tr t ún ú g n g bi b a a lần ầ n lượt là 0, 0 6 6 và 0, 0 7 7 tro t ng n g lần ầ bắ b n ắ n của ủ a mình n . h Tí nh n h xác á suấ u t ấ của a bi b ến ế n cố: ố “Bạn ạ n Hạ H nh n h và à Hà H đề đ u ề u bắ b n ắ t rún rú g n b i b a”.
Yeah, Đúng rồi, bạn giỏi quá!
Ồ, tiếc quá, sai mất rồi! A. 0,42 B.0,5 C.0,6 D.0,7 Câ C u 2. 2 Hai a bện ệ h n h nh n â h n â n X và à Y Y bị b nh n iễm ễ vi rút tSARS-COV- V 2. 2 .Biế Bi t ế rằn ằ g n g xác á suất ấ bị b bi b ến ế n chứ h ng n g nặ n n ặ g g của a bệ b n ệ h n nh n â h n â n X là 0,1 , 1 và à của ủ a bện ệ h n h nh n â h n n Y Y là 0, 0 2 2 . .Khả Kh nă n n ă g n g bị b bi b ến ế n chứn ứ g n nặ n n ặ g n của ủ a ha h i a bệ b n ệ h h nh n â h n n là à độ đ c ộ lập. p Hã H y títnh n h xác á suấ u t ấ của ủ các á bi b ến ế c ố: ố "Cả ả ha h i a bệ b n ệ h n n h n â h n n đề đ u ề u khô h n ô g n g bị b bi b ến ế n chứ h n ứ g n n ặn ặ g n " g .
Yeah, Đúng rồi, bạn giỏi quá!
Ồ, tiếc quá, sai mất rồi! A. 0,02 B. 0,72 C. 0,3 D. 0,03 Câ C u â 3. 3 Cả C hai ai xạ x thủ cùng bắn vào v bia. Xác suấ s t uấ người ườ thứ nhất nhấ bắn trúng bia bi là l 0,8; ,8 người i thứ ha h i i bắn trúng r bia bi là l 0,7 ,7 . Hã H y ã tính xác x su s ất ấ của biế bi n n cố: c “C “ ả hai hai người ườ cùng i kh cùng ô kh ng bắn ng tr bắn úng” Yeah, Đúng rồi, Ồ, tiếc quá, sai bạn giỏi quá! mất rồi! A. P(B)=0,04 C. P(B)=0,08 B. P(B)=0,06 D. P(B)=0,05
Câu 4. Gieo một con xúc sắc 4 lần. .Tìm
Tìm xác suất của biến cố A: "Mặ M t 4 t chấm xuất h t iện ít n ít hất mộ t t lầ t n" Yeah, Đúng rồi, Ồ, tiếc quá, sai bạn giỏi quá! mất rồi! A. C. B. D. Câ C u â 5. . Hai H ai cầu c thủ sút s phạt phạ đề
đ n. Mỗi ingười iđá 1 lần l vớ v i ixá x c suấ s t uấ đá vào v gôn g tương ứ ng l ng à l 0 à ,8 , v à v 0 ,7 , . Tí T nh í x nh ác x s ác uấ s t uấ đ ể c ó c ít ó nhấ ít t nhấ 1 c ầu c thủ ầu đá đ v á ào v g ôn g . Yeah, Đúng rồi, Ồ, tiếc quá, sai bạn giỏi quá! mất rồi! A. P(X)=0,42 C. P(X)=0,234 B. P(X)=0,94 D. P(X)=0,9 Wow! Bạn th t ậ giỏi đó….
Cảm ơn bạn nhé! Đây là m t ộ chút quà mình dành t n ặ g bạn nè!
Bài 8.11 (SGK – tr.78)
Cho hai biến cố và là hai biến cố xung khắc
với . Chứng tỏ rằng hai biến cố và không độc lập. Giải Ta có Do đó
Vậy hai biến cố và không độc lập. B à i 8 . 1 2 (SG K – tr . 7 8
) Một thùng đựng 60 tấm thẻ cùng loại được đánh số từ
1 đến 60. Rút ngẫu nhiên một tấm thẻ trong thùng. Xét hai biến cố sau:
“Số ghi trên tấm thẻ là ước của 60” và : “Số ghi trên tấm thẻ là ước của 48”.
Chứng tỏ rằng và là hai biến cố không độc lập. Giải Ta có . . B à i 8 . 1 2 (SG K – tr . 7 8
) Một thùng đựng 60 tấm thẻ cùng loại được đánh số từ
1 đến 60. Rút ngẫu nhiên một tấm thẻ trong thùng. Xét hai biến cố sau:
“Số ghi trên tấm thẻ là ước của 60” và : “Số ghi trên tấm thẻ là ước của 48”.
Chứng tỏ rằng và là hai biến cố không độc lập. Giải
Do đó hai biến cố và không độc lập.
Bài 8.13 (SGK – tr.78)
Có hai túi đựng các viên bi có cùng kích thước và khối lượng. Túi I có 3 viên
bi màu xanh và 7 viên bi màu đỏ. Túi II có 10 viên bi màu xanh và 6 viên bi
màu đỏ. Từ mỗi túi, lấy ngẫu nhiên ra một viên bi. Tính xác suất để:
a) Hai viên bi được lấy có cùng màu xanh;
b) Hai viên bi được lấy có cùng màu đỏ;
c) Hai viên bi được lấy có cùng màu;
d) Hai viên bi được lấy không cùng màu. Giải
a) Gọi là biến cố: "Hai viên bi lấy ra cùng màu xanh".
Gọi là biến cố: "Viên bi lấy ra từ túi I có màu xanh",
là biến cố: "Viên bi lấy ra từ túi II có màu xanh". Ta có .
Hai biến cố và độc lập nên . Giải
b) Gọi là biến cố: "Hai viên bi lấy ra cùng màu đỏ".
Gọi là biến cố: "Viên bi lấy ra từ túi I có màu đỏ”,
là biến cố: "Viên bi lấy ra từ túi II có màu đỏ”. Ta có .
Hai biến cố và độc lập nên Giải
c)Ta có mà và xung khắc nên áp dụng công thức cộng xác suất:
d) Gọi là biến cố: "Hai viên bi lấy ra không cùng màu". Ta có . VẬN DỤNG B ài 8 .14 ( S GK – t r . 7 8 )
Có hai túi mỗi túi đựng 10 quả cầu có cùng kích thước
và khối lượng được đánh số từ 1 đến 10. Từ mỗi túi, lấy ngẫu nhiên ra một quả
cầu. Tính xác suất để trong hai quả cầu được lấy ra không có quả cầu nào ghi số 1 hoặc ghi số 5. Giải
Gọi là biến cố: "Hai quả cầu lấy ra không có quả cầu nào mang số 1 ",
là biến cố: "Quả cầu lấy ra từ túi I không mang số 1",
là biến cố: "Quả cầu lấy ra từ túi II không mang số 1 ”. Ta có .
Hai biến cố và độc lập nên . Giải Dễ thấy . Vậy .
Gọi là biến cố: "Hai quả cầu lấy ra không có quả cầu nào mang số 5 ". Tương tự, ta có .
Gọi là biến cố: "Trong hai quả cầu lấy ra không có quả cầu nào mang số 1 hoặc số 5 ”. Ta có .
Theo công thức cộng xác suất ta có Giải
Gọi là biến cố: "Hai quả cẩu lấy ra không có quả cầu nào mang số 1 và mang số 5 "
là biến cố: "Quả cầu lấy ra từ túi không mang số 1 và mang số 5 ",
là biến cố: "Quả cầu lấy ra từ túi II không mang số 1 và mang số 5 ". Ta có . Từ đó . Vậy
Bài 8.15 (SGK – tr.78)
Trong đợt kiểm tra cuối học kì II lớp 11 của các trường trung học phổ thông,
thống kê cho thấy có 93% học sinh tỉnh X đạt yêu cầu; 87% học sinh tỉnh Y đạt
yêu cầu. Chọn ngẫu nhiên một học sinh của tỉnh X và một học sinh của tỉnh Y.
Giả thiết rằng chất lượng học tập của hai tỉnh là độc lập. Tính xác suất để:
a) Cả hai học sinh được chọn đều đạt yêu cầu;
b) Cả hai học sinh được chọn đều không đạt yêu cầu;
c) Chỉ có đúng một học sinh được chọn đạt yêu cầu;
d) Có ít nhất một trong hai học sinh được chọn đạt yêu cầu. Giải
Gọi A là biến cố: "Học sinh tỉnh X đạt yêu cầu".
B là biến cố: “Học sinh tỉnh Y đạt yêu cầu”. a) b) c) d)
HƯỚNG DẪN VỀ NHÀ
 Ghi nhớ kiến thức trong bài
 Hoàn thành các bài tập trong SBT
 Chuẩn bị trước Bài tập cuối chương VIII CẢM ƠN CÁC EM
ĐÃ THEO DÕI TIẾT HỌC!
Document Outline

• Slide 1
• Slide 2
• Slide 3
• Slide 4
• Slide 5
• Slide 6
• Slide 7
• Slide 8
• Slide 9
• Slide 10
• Slide 11
• Slide 12
• Slide 13
• Slide 14
• Slide 15
• Slide 16
• Slide 17
• Slide 18
• Slide 19
• Slide 20
• Slide 21
• Slide 22
• Slide 23
• Slide 24
• Slide 25
• Slide 26
• Slide 27
• Slide 28
• Slide 29
• Slide 30
• Slide 31
• Slide 32
• Slide 33
• Slide 34
• Slide 35
• Slide 36
• Slide 37
• Slide 38
• Slide 39
• Slide 40
• Slide 41
• Slide 42