Giáo án điện tử Toán 11 Chương 6 Bài 4 Cánh diều: Phương trình, bất phương trình mũ và logarit

CHÀO MỪNG TẤT CẢ CÁC EM
ĐẾN VỚI TIẾT HỌC! KHỞI ĐỘNG
Giả sử giá trị còn lại (tính theo triệu đồng) của một chiếc ô tô
sau năm sử dụng được mô hình hóa bằng công thức:
Hỏi nếu theo mô hình này, sau bao nhiêu năm sử dụng thì giá trị
của chiếc ô tô đó còn lại không quá triệu đồng? (Làm tròn kết
quả đến hàng đơn vị).
CHƯƠNG VI: HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
BÀI 4. PHƯƠNG TRÌNH, BẤT PHƯƠNG TRÌNH MŨ VÀ LÔGARIT NỘI DUNG BÀI HỌC
Phương trình mũ và I
Phương trình lôgarit
Bất phương trình mũ và II
Bất phương trình lôgarit I PHƯƠNG TRÌNH MŨ VÀ PHƯƠNG TRÌNH LÔGARIT 1. 1 Phương trì nh mũ
 HĐ1: Trong bài toán ở phần mở đầu, giả sử / năm.
a) Viết phương trình thể hiện dân số sau năm gấp đôi dân số ban đầu.
b) Phương trình vừa tìm được có ẩn là gì và nằm ở vị trí nào của luỹ thừa? Giải: a) Ta có
b) Ẩn trong phương trình trên là , nằm trong lũy thừa của số , tức là . KẾT LUẬN
Phương trình mũ là phương
trình có chứa ẩn ở số mũ của lũy thừa.
Ví dụ 1: Trong các phương trình sau, phương trình nào là phương trình mũ?
𝑎¿ 5𝑥2+1=25 ; 𝑏 ¿ 2𝑥=3𝑥+1 ;
𝑐 ¿ 𝑥2= 4. Giải
Ta thấy: Hai phương trình và là những phương trình mũ. Luyện tập 1
Cho hai ví dụ về phương trình mũ. Giải 1) ; 2)
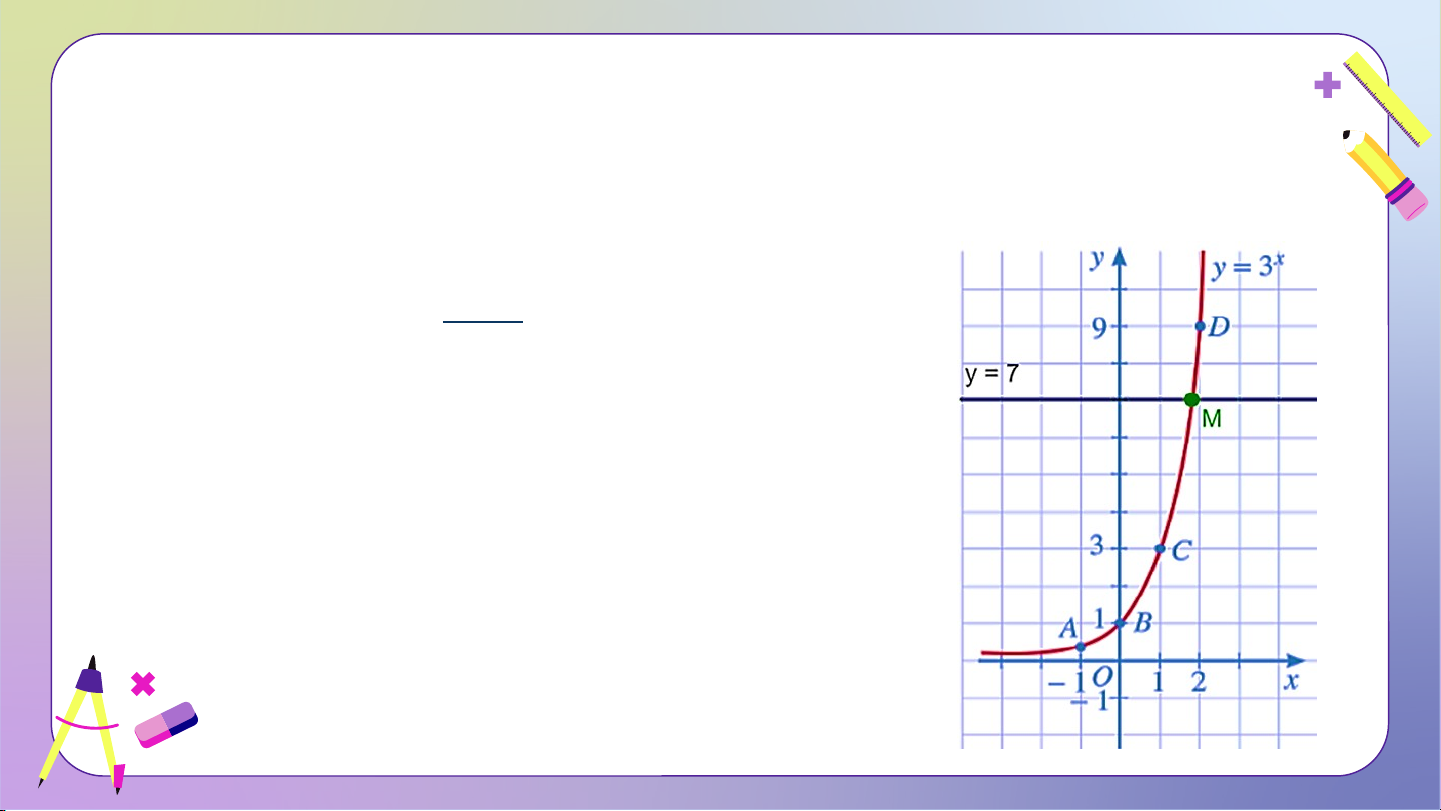
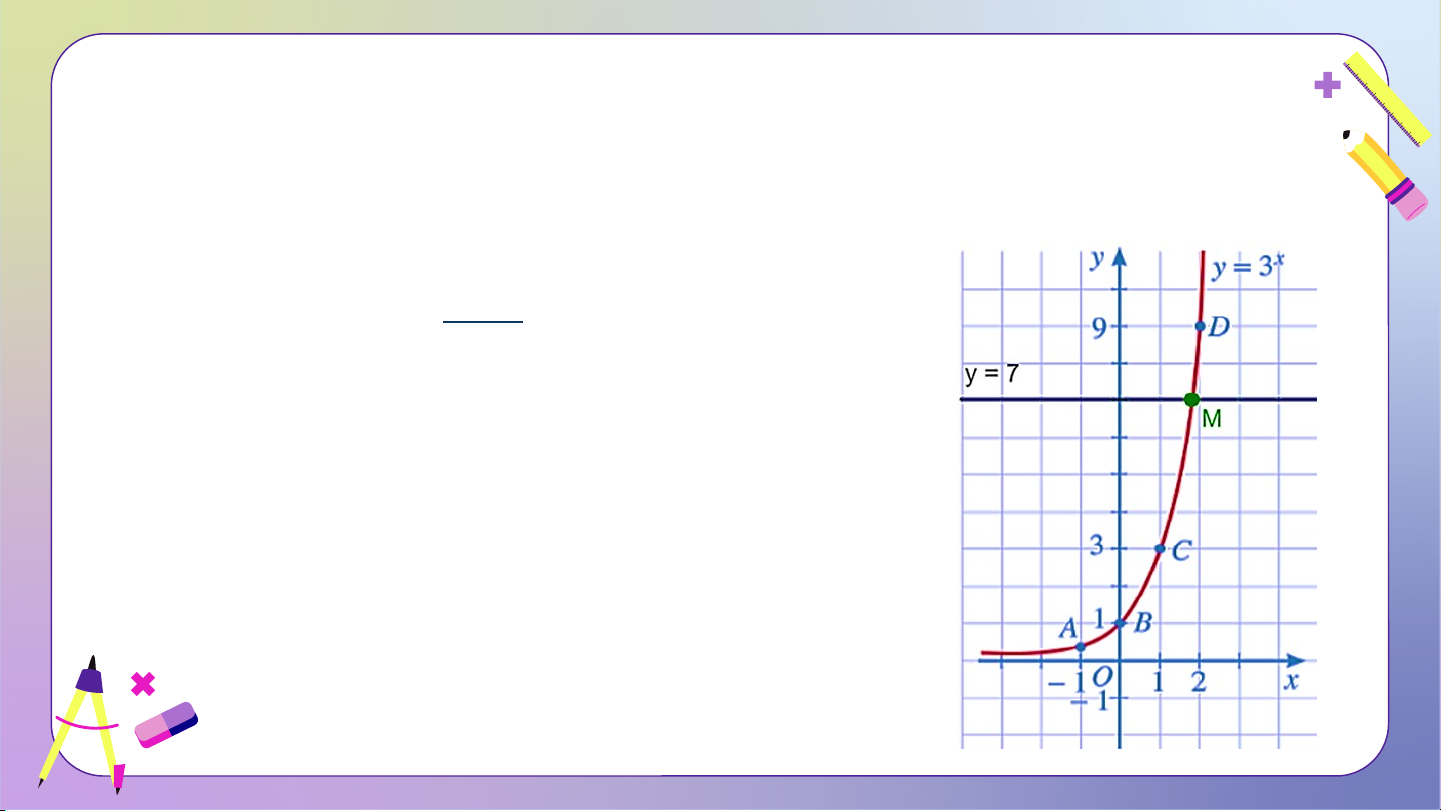
 HĐ2: a) Vẽ đồ thị hàm số và đường thẳng .
b) Nhận xét về số giao điểm của hai đồ thị trên. Từ đó, hãy nêu nhận xét
về số nghiệm của phương trình . Giải:
a) Ta thấy hàm số có cơ số
• Đồ thị của hàm số đi qua các điểm
• Đường thẳng đi qua điểm và song song với .
 HĐ2: a) Vẽ đồ thị hàm số và đường thẳng .
b) Nhận xét về số giao điểm của hai đồ thị trên. Từ đó, hãy nêu nhận xét
về số nghiệm của phương trình . Giải:
b) Đồ thị hàm số giao đường thẳng tại 1 điểm duy nhất.
Phương trình có 1 nghiệm duy nhất. KẾT LUẬN
Phương trình mũ cơ bản ẩn có dạng
• Nếu thì phương trình vô nghiệm.
• Nếu thì phương trình có nghiệm duy nhất .
Nhận xét: Với thì Ch C ú h ú ý
Phương pháp giải phương trình mũ bằng cách đưa về cùng cơ số: Nếu thì
Ví dụ 2: Giải mỗi phương trình sau: Giải: Ta có: 1
𝑎¿ 42𝑥−3=5 ⇔ 2 𝑥 − 3=𝑙𝑜𝑔4 5 ⇔ 2 𝑥 =3+𝑙𝑜𝑔4 5 ⇔ 𝑥= 2 (3+𝑙𝑜𝑔45)
Vậy phương trình có nghiệm là
𝑏¿ 10𝑥+1 −2. 10𝑥=8 ⇔ 10.10𝑥 −2. 10𝑥=8 ⇔ 8. 10𝑥=8 ⇔ 10𝑥=1
⇔ 𝑥=𝑙𝑜𝑔1 ⇔ 𝑥=0
Vậy phương trình có nghiệm là
Ví dụ 3: Giải phương trình Giải: Ta có:
Vậy phương trình có nghiệm là Chú ý: Với thì: Chú ý: Với thì:
Ví dụ 4: Giải phương trình đưa ra trong Hoạt động 1 (làm tròn
kết quả đến hàng đơn vị). Giải:
Gọi là dân số ban đầu. Phương trình thể hiện dân số sau năm
gấp đôi dân số ban đầu là:
Vậy sau khoảng năm dân số sẽ gấp đôi dân số ban đầu. Luyện tập 2
Giải mỗi phương trình sau:
a¿ 916−𝑥=27𝑥+4;b¿16𝑥−2=0,25.2−𝑥+4 Giải 2. 2 .Phư P ơng t g rình l ôg l ari a t ri
 HĐ3: Chỉ số hay độ của một dung dịch được tính theo công thức:
(trong đó chỉ nồng độ ion hydrogen). Đo chỉ số của một mẫu nước sông, ta có kết quả là .
a) Viết phương trình thể hiện nồng độ của hydrogen trong mẫu nước sông đó.
b) Phương trình vừa tìm được có ẩn là gì và nằm ở vị trí nào của lôgarit? Giải: a) Ta có:
b) Phương trình vừa tìm được có ẩn là và nằm ở vị trí hệ số của lôgarit. KẾT LUẬN
Phương trình lôgarit là phương trình có chứa ẩn
trong biểu thức dưới dấu lôgarit.
Ví dụ 5: Trong các phương trình sau, phương trình nào là phương trình lôgarit? Giải: Hai phương trình: và
là những phương trình lôgarit Luyện tập 3
Cho hai ví dụ về phương trình lôgarit. Giải 1) ; 2)
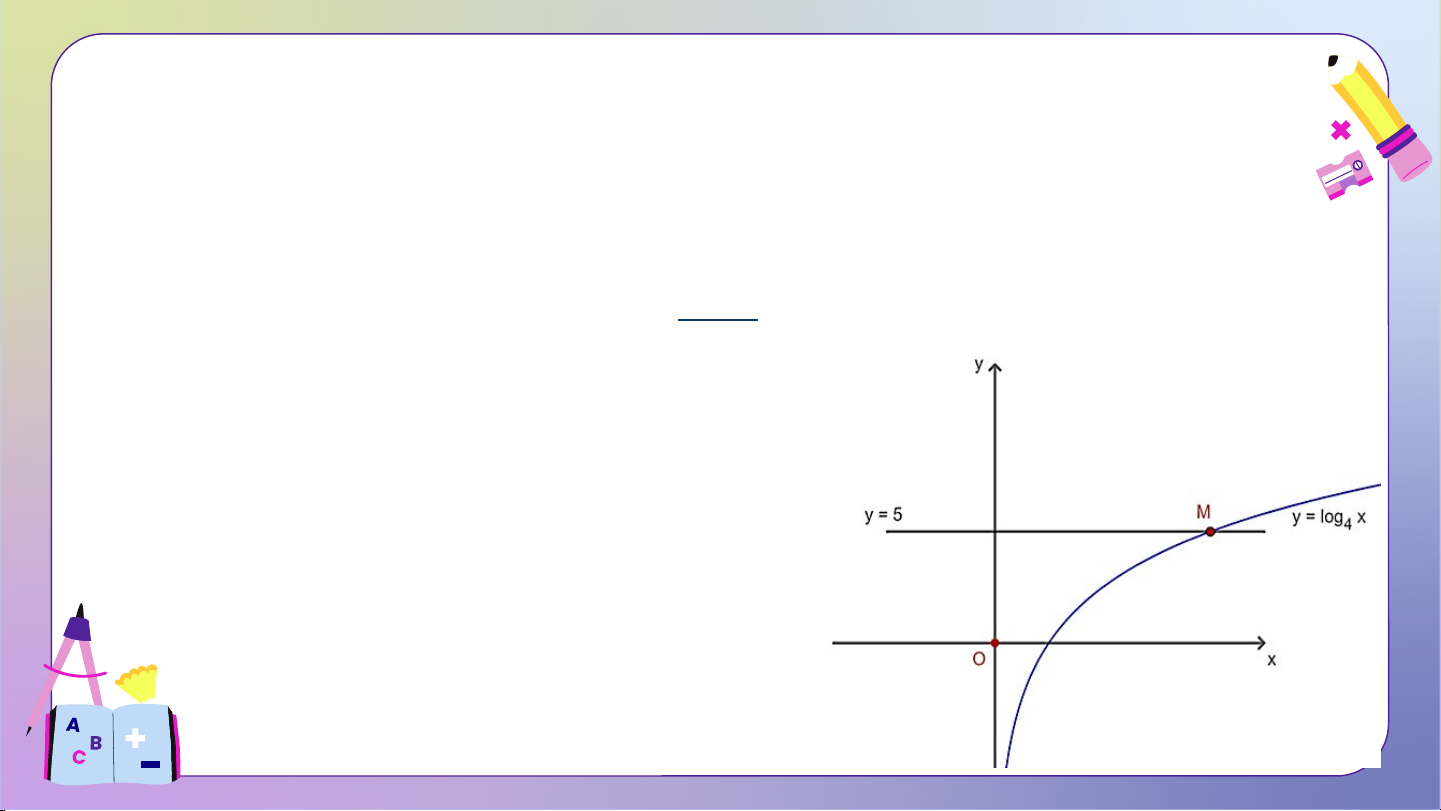
 HĐ4: a) Vẽ đồ thị hàm số và đường thẳng .
b) Nhận xét về số giao điểm của hai đồ thị trên. Từ đó, hãy nêu nhận xét
về số nghiệm của phương trình . Giải: a) Vì hàm số có cơ số
• Đồ thị hàm số đi qua các điểm .
• Đường thẳng đi qua điểm và song song với trục .
 HĐ4: a) Vẽ đồ thị hàm số và đường thẳng .
b) Nhận xét về số giao điểm của hai đồ thị trên. Từ đó, hãy nêu nhận xét
về số nghiệm của phương trình . Giải:
b) Đồ thị hàm số và đường thẳng
cắt nhau tại 1 điểm duy nhất.
Phương trình có 1 nghiệm duy nhất. KẾT LUẬN
Phương trình lôgarit cơ bản có dạng
Phương tình đó có nghiệm duy nhất là
Nhận xét: Với thì .
Ví dụ 6: Giải các phương trình sau a) b) Giải: a) Ta có: .
Vậy phương trình có nghiệm là b) Ta có: .
Vậy phương trình có nghiệm là
Ví dụ 7: Giải phương trình: Giải:
Điều kiện xác định là tức là . Ta có:
Vậy phương trình có nghiệm Chú ý Cho . Ta có:
Ví dụ 8: Giải phương trình đưa ra trong Hoạt động 3. Giải:
Phương trình thể hiện nồng độ của ion hydrogen trong mẫu nước sông đó là:
Vậy nồng độ của ion hydrogen trong mẫu nước sông đó là
Luyện tập 4 Giải mỗi phương trình sau: a) Giải: a)
Vậy nghiệm của phương trình là .
Luyện tập 4 Giải mỗi phương trình sau: a) Giải: ĐKXĐ: (tmđk)
Vậy nghiệm của phương trình là . II
BẤT PHƯƠNG TRÌNH MŨ VÀ
BẤT PHƯƠNG TRÌNH LÔGARIT 1. 1 Bất B ất phương trì n trì h mũ
HĐ5: Quan sát Hình 11 và nêu nhận xét về tính
đồng biến, nghịch biến của hàm số mũ . Từ đó, hãy tìm sao cho Giải:
• Hàm số nghịch biến trên .
• Quan sát đồ thị ta thấy, để thì . KẾT LUẬN
• Bất phương trình mũ là bất phương trình có chứa ẩn ở số mũ của lũy thừa.
• Bất phương trình mũ cơ bản là bất phương trình mũ có một trong các dạng sau:
Ví dụ 9: Bất phương trình nào là bất phương trình mũ cơ bản
trong các bất phương trình sau? Giải:
Ta thấy: Hai bất phương trình và là những bất phương trình mũ cơ bản. Luyện tập 5
Cho hai ví dụ về bất phương trình mũ cơ bản. Giải 1) ; 2)
Cách giải bất phương trình mũ
Xét bất phương trình mũ:
• Nếu , tập nghiệm của bất phương trình đã cho là (vì ).
• Nếu thì bất phương trình tương đương với
Với , nghiệm của bất phương trình là
Với , nghiệm của bất phương trình là . Chú ý: Với thì Với thì
Ví dụ 10: Giải mỗi bất phương trình sau: Giải: Ta có:
𝑎¿ 5𝑥>12 ⇔ 𝑥 >𝑙𝑜𝑔 12 5
Vậy tập nghiệm của bất phương trình là
Vậy tập nghiệm của bất phương trình là Luyện tập 6
Giải mỗi bất phương trình sau: Giải:
Vậy tập nghiệm của bất phương trình là .
Vậy tập nghiệm của bất phương trình là: . Ví dụ 1 1:
Dân số Việt Nam năm 2021 ước tính là A = 98 564 407 người.
(Nguồn: https://danso.org/viet-nam) Giả sử tỉ lệ tăng dân số hàng năm của
Việt Nam là . Biết rằng sau năm, dân số Việt Nam (tính từ mốc năm 2021)
ước tính theo công thức: . Hỏi từ năm nào trở đi, dân số Việt Nam vượt quá 110 triệu người? Giải: Ta có: Suy ra .
Vậy sau 12 năm tính từ mốc năm 2021, tức là từ năm 2033 trở đi, dân số
Việt Nam vượt quá 110 triệu người. 2. 2 Bấ B t ấ phương trìn trì h lôgari ôgar t
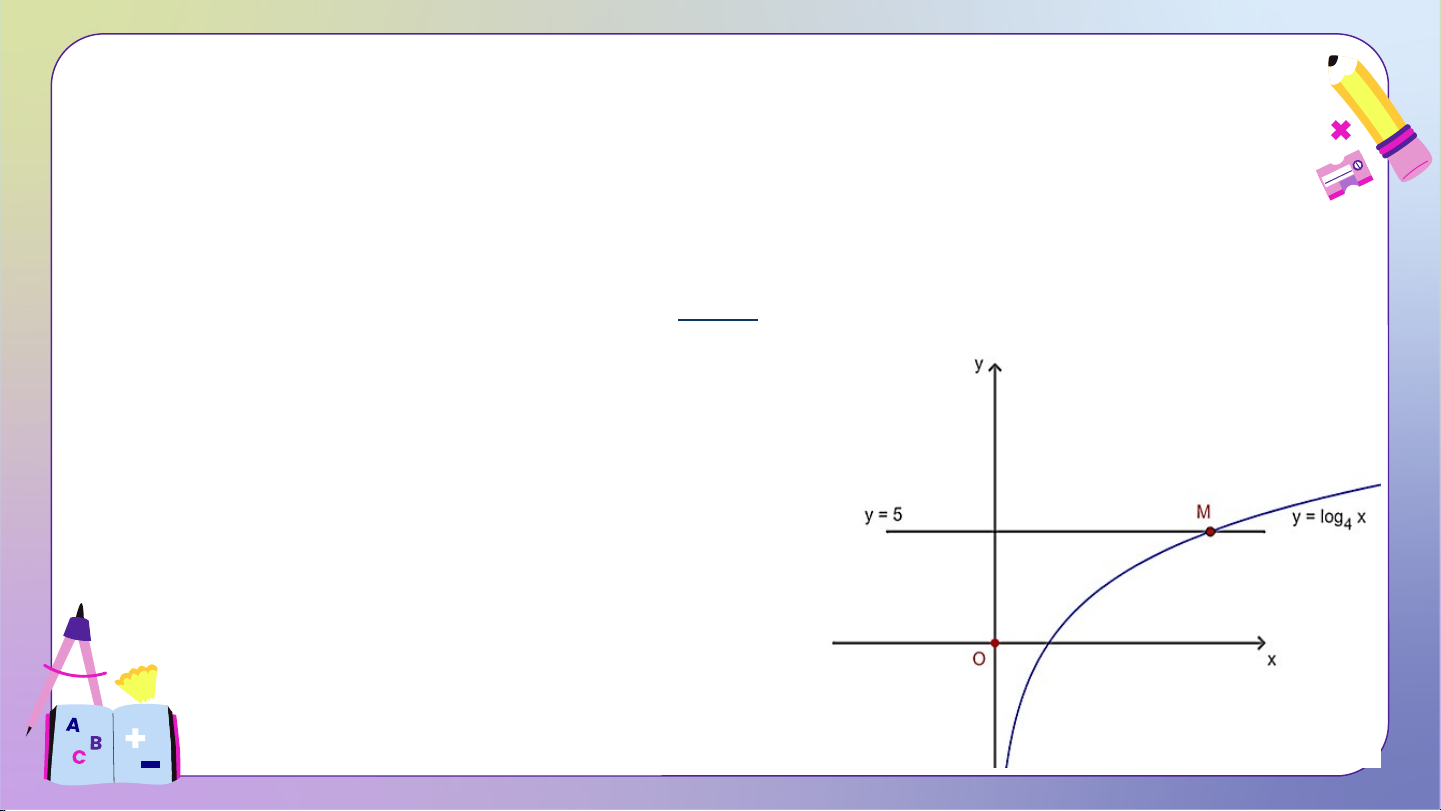
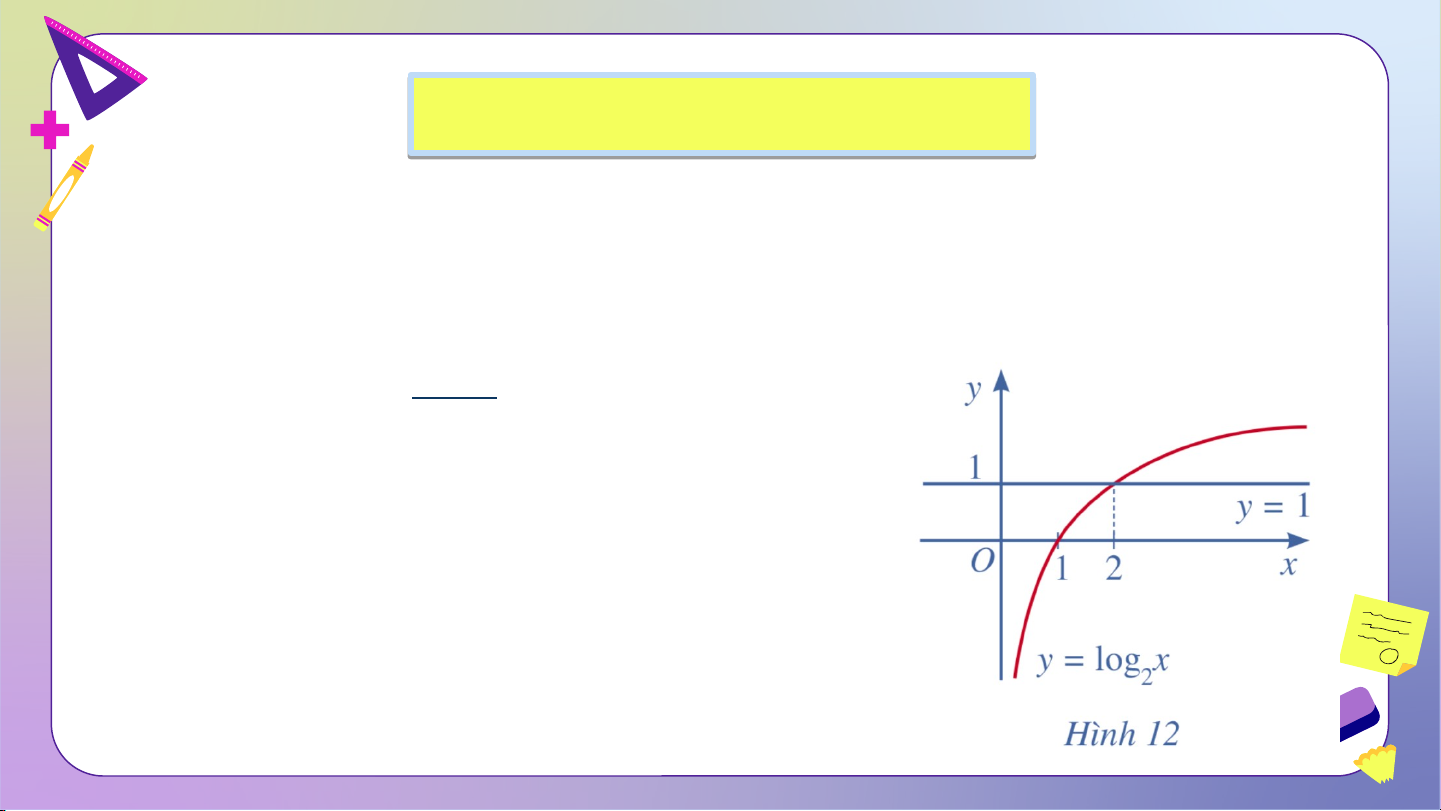
HĐ6: Quan sát Hình 12 và nêu nhận xét về tính đồng biến, nghịch biến
của hàm số lôgarit . Từ đó, hãy tìm sao cho . Giải:
• Hàm số đồng biến trên tập xác định.
• Quan sát đồ thị ta thấy, để thì . KẾT LUẬN
• Bất phương trình lôgarit là bất phương trình có chứa ẩn
trong biểu thức dưới dấu lôgarit.
• Bất phương trình lôgarit cơ bản là bất phương trình lôgarit
có một trong những dạng sau:
Ví dụ 12: Bất phương trình nào là bất phương trình
lôgarit cơ bản trong các bất phương trình sau? Giải:
Ta thấy: Hai bất phương trình: và
là những bất phương trình lôgarit cơ bản. Luyện tập 7
Cho hai ví dụ về bất phương trình lôgarit cơ bản. Giải 1) ; 2)
Cách giải bất phương trình lôgarit Xét bất phương trình
Bất phương trình tương đương với
• Với , nghiệm của bất phương trình là
• Với , nghiệm của bất phương trình là . Chú ý: Với thì Với thì Ví dụ 13:
Giải mỗi bất phương trình sau: Giải:
Vậy tập nghiệm của bất phương trình là
Vậy tập nghiệm của bất phương trình là Luyện tập 8
Giải mỗi bất phương trình sau: a) b) Giải: a)
Vậy tập nghiệm của bất phương trình là . b)
Vậy tập nghiệm của bất phương trình là V í d ụ 1 4
: Mức cường độ âm (đơn vị: ) được tính bởi công thức
trong đó (đơn vị: ) là cường độ âm (Nguồn: Vật lí 12, NXBGD Việt
Nam, 2021). Mức cường độ âm ở một khu dân cư được quy định là
dưới . Hỏi cường độ âm ở khu vực đó phải dưới bao nhiêu ? Giải: Ta có:
Vậy cường độ âm ở khu vực đó phải dưới LUYỆN TẬP Đến giờ câu cá rồi. Các em hãy giúp ông nhé
Câu 1. Nghiệm của phương trình là? A. C. B. D. S A ai mất Sai mất Sai mất rồi B rồi C D rồi
Câu 2. Tập nghiệm của bất phương trình là ? A. C. B. D. S Sai mất Sai mất A ai mất rồi B Crồi Drồi
Câu 3. Nghiệm của phương trình là A. C. B. D. S A ai mất Sai mất Sai mất rồi B rồi Crồi D
Câu 4. Tập nghiệm của bất phương trình là A. C. B. D. S A ai mất Sai mất Sai mất rồi B rồi C D rồi
Câu 5. Tổng bình phương các nghiệm của phương trình bằng A. C. B. D. S Sai mất Sai mất A ai mất rồi B Crồi Drồi Ông cảm ơn các em giúp ông lão câu cá! Bài 1 (SGK – tr.54)
Giải mỗi phương trình sau: 𝑎 ¿ ¿ 4
𝑏¿ 53 𝑥−2=25 ⇔ 𝑥= 3
𝑐 ¿ 9𝑥−2=24 3𝑥+1 d) e) ; ĐKXĐ: (tmđk) g) ; ĐKXĐ: (tmđk) Bài 1 (SGK – tr.54)
Giải mỗi phương trình sau:
𝑑¿𝑙𝑜𝑔1(¿𝑥+1)=−3¿ ⇔𝑥=7 2
𝑒¿𝑙𝑜𝑔 ĐKXĐ:
5(¿ 3 𝑥 −5)=𝑙𝑜𝑔5( ¿ 2 𝑥 +1)¿ ¿ ⇔𝑥¿6 ( tmđk)
𝑑 ¿𝑙𝑜𝑔1(¿ 𝑥+9)=𝑙𝑜𝑔1 (¿2 𝑥−1);¿¿ ĐKXĐ: 7 7 ⇔𝑥¿10 (tmđk) Bài 2 (SGK – tr.55)
Giải mỗi bất phương trình sau: 1
𝑎¿ 3𝑥> 243 ⇔𝑥>−5 3 𝑥−7 3 𝑏¿(2 ≤ 3 ) 2 ⇔ 𝑥 ≥2
𝑐 ¿ 4𝑥+3≥ 3 2𝑥 Bài 2 (SGK – tr.55)
Giải mỗi bất phương trình sau:
𝑑¿𝑙𝑜𝑔(¿𝑥−1)<0¿ ⇔1<𝑥<2
𝑒¿𝑙𝑜𝑔 1
1 (¿ 2 𝑥 −1)≥ 𝑙𝑜𝑔1 (¿ 𝑥 +3)¿ ¿ ⇔ 5 5 2 <𝑥≤ 4
𝑔¿𝑙𝑛(¿ 𝑥+3)≥𝑙𝑛(¿2 𝑥−8)¿¿ ⇔ 4 < 𝑥 ≤ 11 VẬN DỤNG Bài 3 (SGK – tr.55)
Một người gửi ngân hàng 100 triệu đồng theo hình thức lãi kép có
kì hạn là 12 tháng với lãi suất /năm Sau 3 năm, người đó rút được
cả gốc và lãi là 119,1016 triệu đồng. Tìm , biết rằng lãi suất không
thay đổi qua các năm và người đó không rút tiền ra trong suốt quá trình gửi. Giải: Ta có :
Vậy lãi suất mà người đó gửi vào ngân hàng theo hình thức
lãi kép có kì hạn 12 tháng là %/năm Bài 4 (SGK – tr.55)
Sử dụng công thức tính mức cường độ âm ở Ví dụ 14,
hãy tính mức cường độ âm mà tai người có thể chịu
đựng được, biết rằng giá trị cực đại của mức cường độ
âm mà tai người có thể chịu đựng được là . Giải: Ta có : Theo đề bài :
Vậy cường độ âm mà tai người có thể chịu được là .
HƯỚNG DẪN VỀ NHÀ Ghi nhớ Hoàn thành Chuẩn bị trước kiến thức các bài tập
bài tập cuối trong bài trong SBT chương VI CẢM ƠN CÁC EM
ĐÃ THEO DÕI TIẾT HỌC!
Document Outline

• Slide 1
• KHỞI ĐỘNG
• Slide 3
• II
• I
• 1. Phương trình mũ
• KẾT LUẬN
• Slide 8
• Slide 9
• Slide 10
• Slide 11
• KẾT LUẬN
• Slide 13
• Slide 14
• Slide 15
• Slide 16
• Slide 17
• 2. Phương trình lôgarit
• KẾT LUẬN
• Slide 20
• Slide 21
• Slide 22
• Slide 23
• KẾT LUẬN
• Slide 25
• Slide 26
• Slide 27
• Slide 28
• Slide 29
• Slide 30
• BẤT PHƯƠNG TRÌNH MŨ VÀ BẤT PHƯƠNG TRÌNH LÔGARIT
• 1. Bất phương trình mũ
• KẾT LUẬN
• Slide 34
• Slide 35
• Slide 36
• Slide 37
• Slide 38
• Slide 39
• 2. Bất phương trình lôgarit
• KẾT LUẬN
• Slide 42
• Slide 43
• Slide 44
• Slide 45
• Slide 46
• Slide 47
• LUYỆN TẬP
• Slide 49
• Slide 50
• Slide 51
• Slide 52
• Slide 53
• Slide 54
• Slide 55
• Slide 56
• Slide 57
• Slide 58
• Slide 59
• VẬN DỤNG
• Slide 61
• Slide 62
• Slide 63
• Slide 64
• HƯỚNG DẪN VỀ NHÀ
• Slide 66