

















Preview text:
CHƯƠNG IV: HÀM SỐ MŨ & HÀM SỐ LÔGARIT
BÀI 4: PHƯƠNG TRÌNH,
BẤT PHƯƠNG TRÌNH MŨ & LÔGARIT
Lớp giảng dạy: 11A1
Giáo sinh giảng dạy: Trần Văn Kiệt NỘI DUNG BÀI HỌC PHƯƠNG TRÌNH LUYỆN I. III. MŨ TẬP PHƯƠNG TRÌNH VẬN II. IV. LÔGARIT DỤNG KHỞI ĐỘNG
Dân số được ước tính theo công thức Trong đó: là dân số c Hỏi saủa u năm l bao ấy làm nhiêu m n ốc ă t m,í nh, là dân số sau t năm ,
dân số sẽ gấp đôi dân
là tỷ lệ dân số hàng năm. số của năm lấy làm mốc tính? HOẠT ĐỘNG 1
Dân số được ước tính theo công thức
Trong đó: là dân số của năm lấy làm mốc tính, là dân số sau năm ,
là tỷ lệ dân số hàng năm.
1. Viết phương trình thể hiện dân số sau năm gấp đôi dân số ban đầu.
2. Phương trình vừa tìm được có ẩn là gì và nằm ở vị trí nào của luỹ thừa? HOẠT ĐỘNG 1
Dân số được ước tính theo công thức
Trong đó: là dân số của năm lấy làm mốc tính, là dân số sau năm ,
là tỷ lệ dân số hàng năm. Giả sử /năm.
1. Phương trình thể hiện dân số sau năm gấp đôi dân số ban
đầu là: 𝐴. 𝑒0,0114 .𝑡=2 𝐴 ⇔ 𝑒0,0114.𝑡=2
2. Phương trình vừa tìm được có ẩn là và nằm ở vị trí số mũ. I. PHƯƠNG TRÌNH MŨ
- Định nghĩa: Phương trình mũ là phương trình
có chứa ẩn ở số mũ của luỹ thừa. Phương trình
mũ cơ bản ẩn x có dạng
Ví dụ 1. Trong các phương trình sau, phương trình nào là phương trình mũ? a) .b) . c) . ✔ ✔ ✘
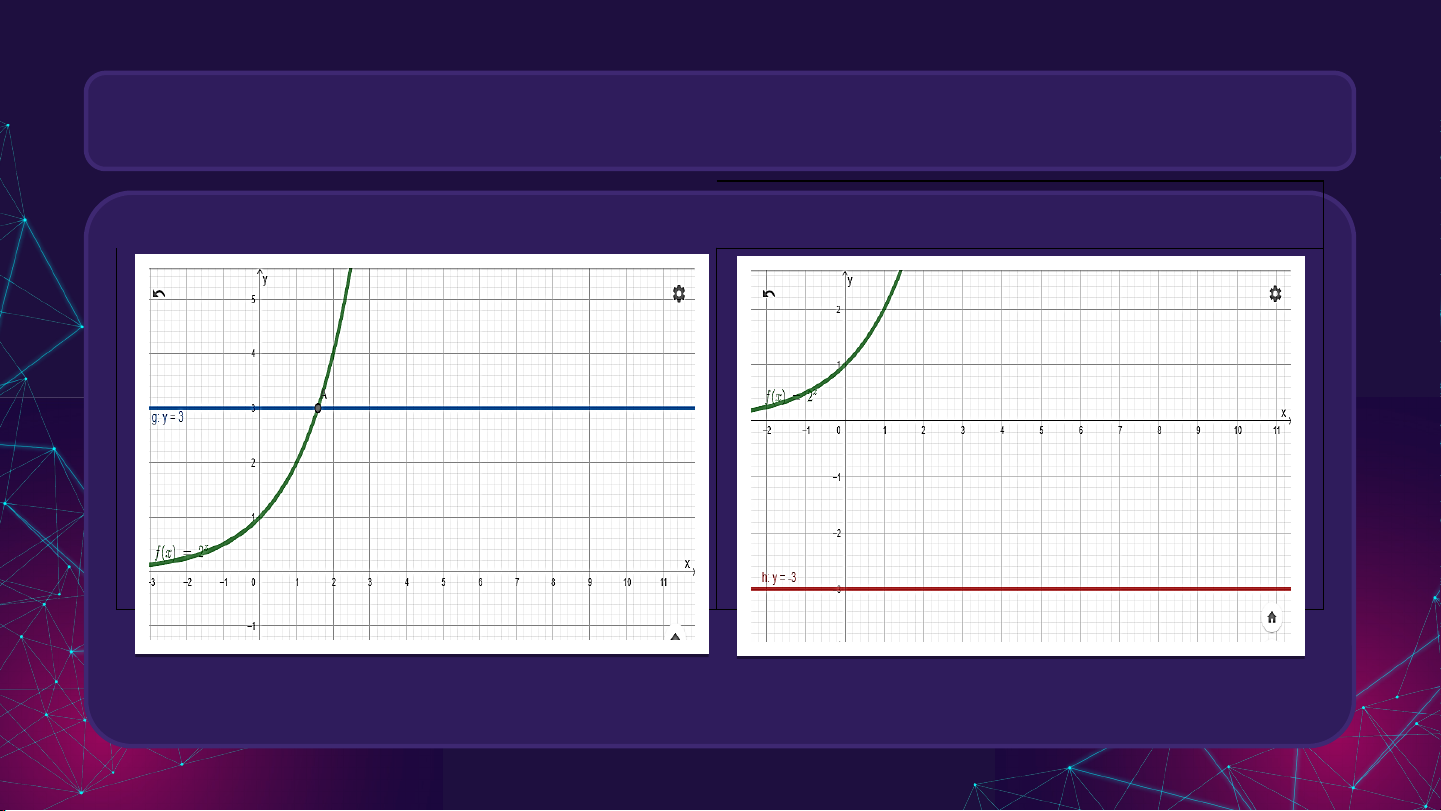
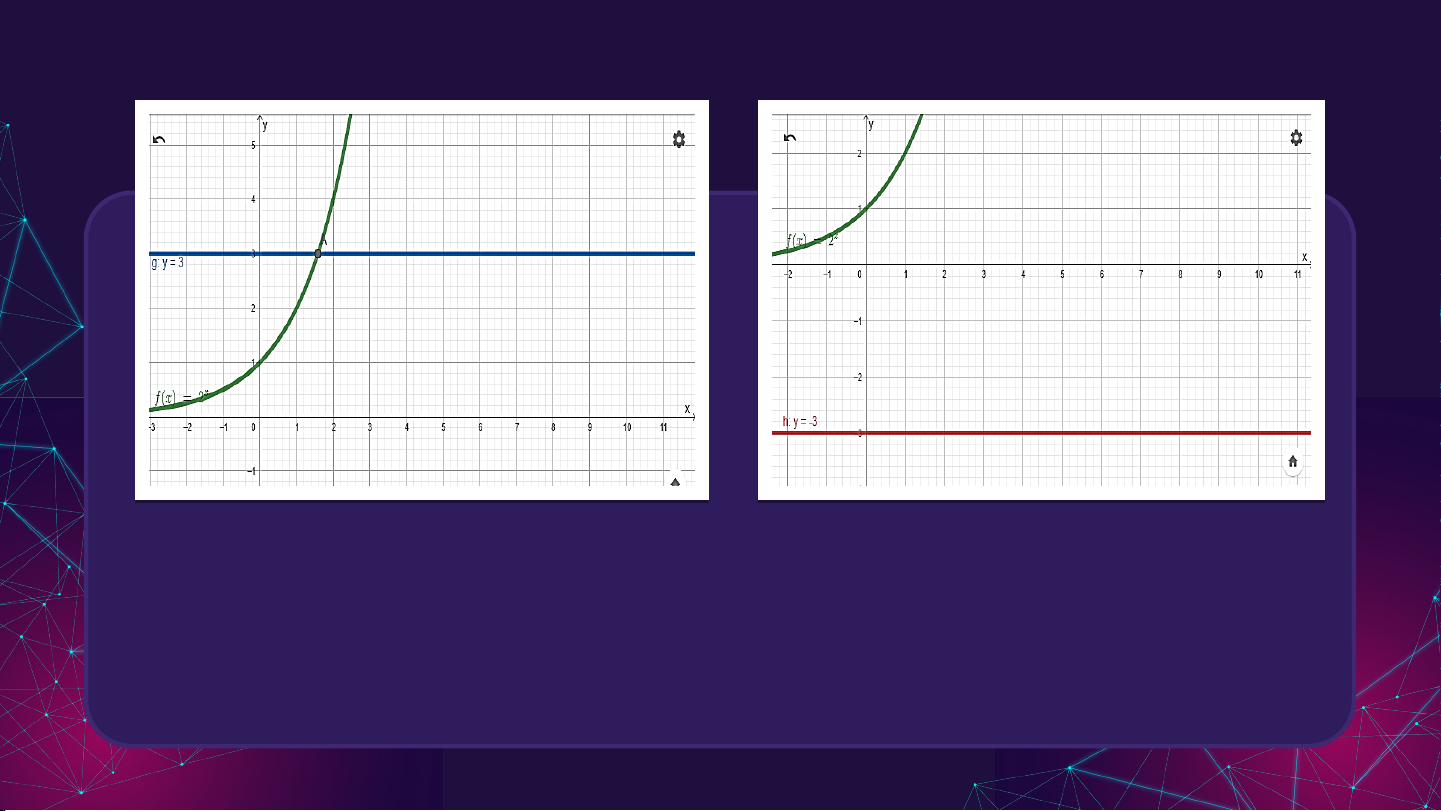
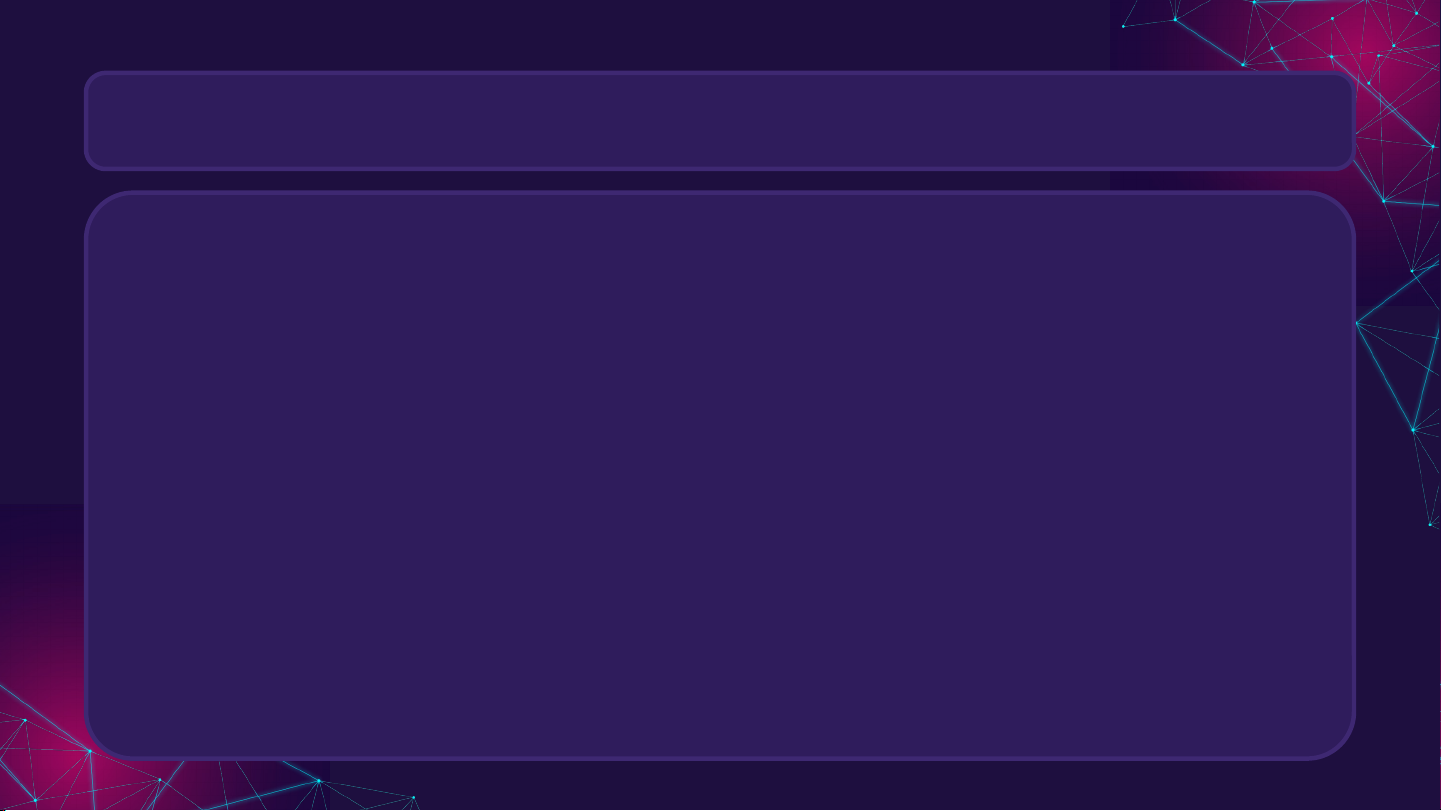
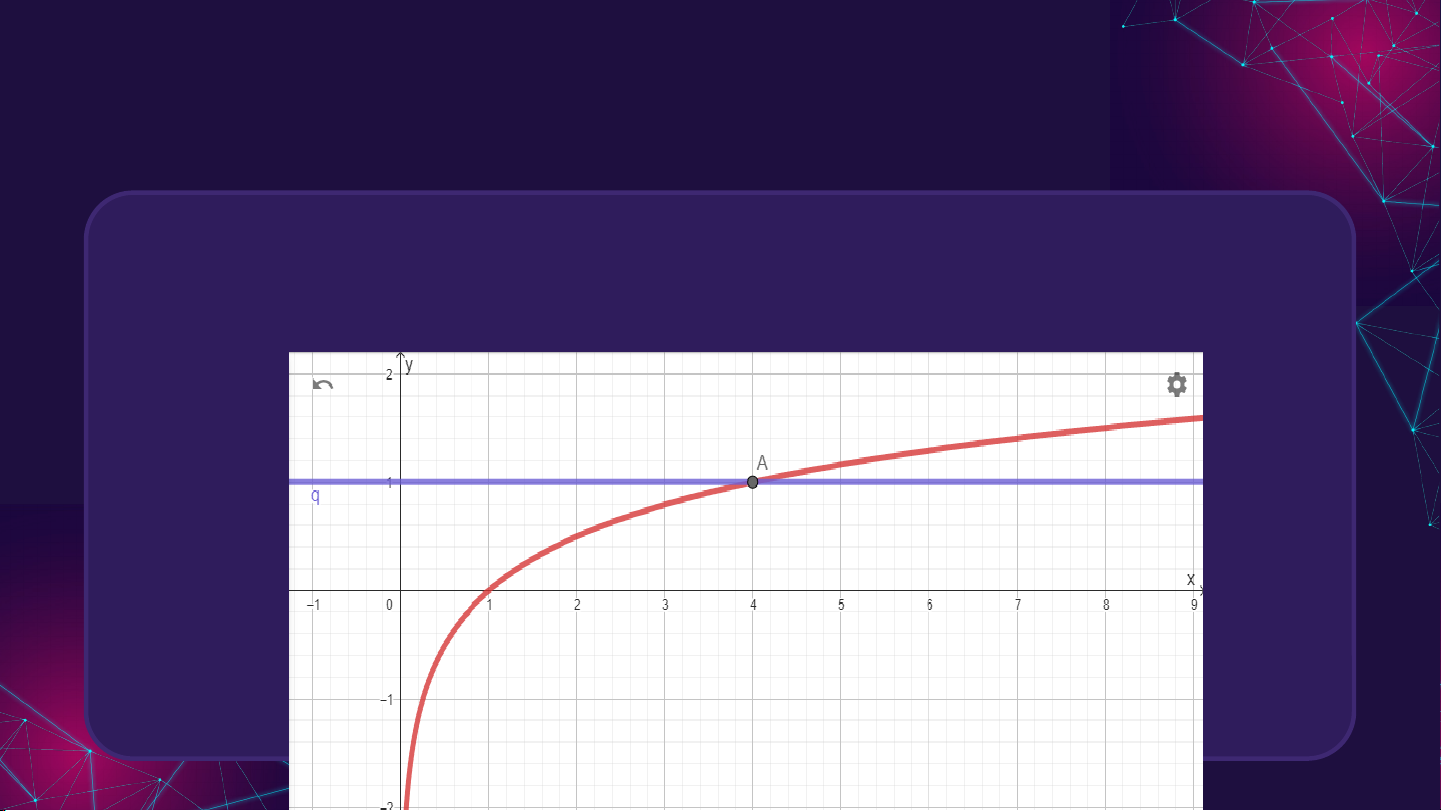
Hình vẽ hoạt động 2 = 3 =
? Quan sát, nhận xét về số giao điểm của hai đồ thị trên. = 3 =
Ở phương trình mũ có một giao điểm.
Ở phương trình mũ không có giao điểm.
Số nghiệm của phương trình chính bằng số giao điểm.
Nghiệm của phương trình . I. PHƯƠNG TRÌNH MŨ Kết luận:
Phương trình mũ cơ bản ẩn có dạng .
Nếu thì phương trình vô nghiệm.
Nếu thì phương trình có nghiệm duy nhất .
Nhận xét: Với thì . Ví dụ 2.
Giải mỗi phương trình sau: a) ; b) . (BTVN) Ví dụ 2 Gi :
ải mỗi phương trình sau: a) ; Ta có:
Vậy phương trình có nghiệm .
Cách giải phương trình mũ cơ bản
Đưa về cùng cơ số. Với thì . Ví dụ 2
Gi:ải mỗi phương trình sau: b) Ta có: .
Vậy phương trình có nghiệm là .
Ví dụ 3: Hoạt động 1 đầu bài. Lời giải. Ta có: Giải phương trình
Hỏi sau bao nhiêu năm, dân số sẽ
gấp đôi dân số của năm lấy làm gốc?
Vậy sau khoảng 61 năn dân số sẽ
tăng gấp đôi dân số ban đầu. HOẠT ĐỘNG 3
Chỉ số thay đổi pH của một dung dịch được tính theo công
thức: (trong đó chỉ nồng độ ion hydrogen). Đo chỉ số pH của
một số mẫu nước sông, ta có kết quả là .
a) Viết phương trình thể hiện nồng độ x của hydrogen trong mẫu nước sông đó.
b) Phương trình vừa tìm được có ẩn là gì và nằm ở vị trí nào của lôgarit?
II. PHƯƠNG TRÌNH LÔGARIT
a) Viết phương trình thể hiện nồng độ của
hydrogen trong mẫu nước sông đó?
b) Phương trình vừa tìm được có ẩn là gì và nằm ở vị trí nào của lôgarit?
Phương trình có ẩn là và nằm dưới dấu lôgarit.
II. PHƯƠNG TRÌNH LÔGARIT
Định nghĩa: Phương trình lôgarit là phương trình có chứa
ẩn trong biểu thức dưới dấu lôgarit. Phương trình lôgarit cơ bản có dạng
Ví dụ 5: Trong các phương trình sau, phương trình nào là phương trình lôgarit? a) ✔ b) ✔ c) ✘ HOẠT ĐỘNG 4
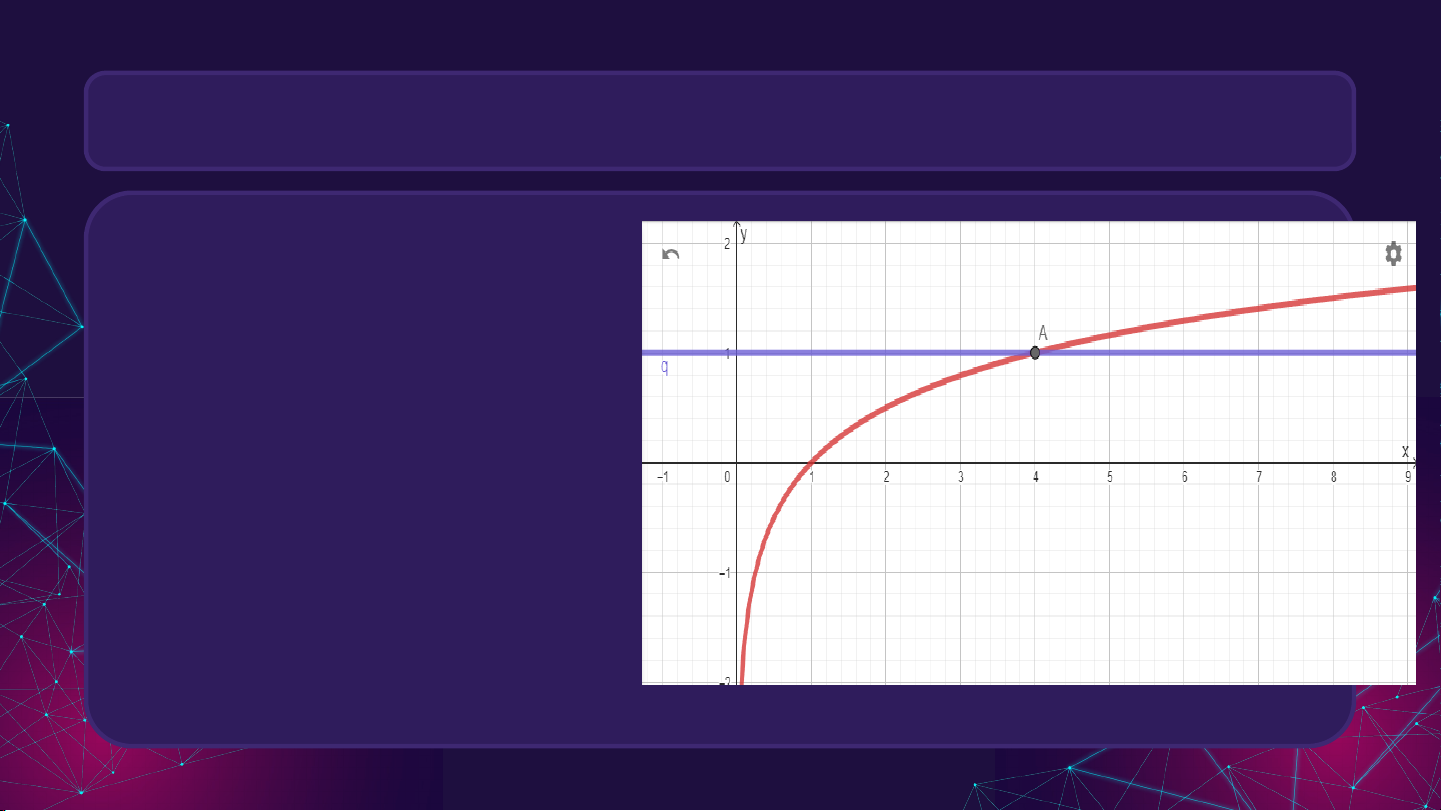
b) Quan sát, nhận xét về số giao điểm của hai đồ thị
trên. Từ đó, hãy nêu nhận xét về số nghiệm của phương trình .
Hình vẽ hoạt động 4 Có một giao điểm.
Số nghiệm của phương trình chính là số giao điểm.
Nghiệm của phương trình .
II. PHƯƠNG TRÌNH LÔGARIT Kết luận:
Phương trình lôgarit cơ bản có dạng
Phương trình có nghiệm duy nhất .
Nhận xét: Với thì .
Cách giải phương trình logarit cơ bản
Đưa về cùng cơ số Cho
Ví dụ 5. Giải phương trình sau: Điều kiện xác định: Ta có:
hoặc (không thỏa mãn ĐKXĐ)
Vậy phương trình có tập nghiệm là II LUYỆN I. TẬP PHIẾU HỌC TẬP
Giải mỗi phơng trình sau: 𝑎) b) IV VẬN . DỤNG VẬN DỤNG
Bài toán 1: Bác Minh gửi tiết kiệm 500 triệu đồng ở một ngân hàng với
lãi suất không đổi 7,5% một năm theo thể thức lãi kép kì hạn 12 tháng.
Tổng số tiền bác Minh thu được (cả vốn lẫn lãi) saunăm là
(triệu đồng). Tính thời gian tối thiểu gửi tiết kiệm để bác Minh thu được
800 triệu đồng (cả vốn lẫn lãi). Bài giải Sử dụng công thức
Để bác Minh thu được 800 triệu đồng (cả vốn lẫn lãi) thì = 800 ⇔
Vậy bác Minh cần khoảng 6,5 năm để thu được 800 triệu đồng (cả vốn lẫn lãi). TRÒ CHƠI AI LÀ TRIỆU PHÚ
Câu 1: Khẳng định nào dưới đây đúng? A. . B. . C. . D..
Câu 2: Cho phương trình . Khẳng định nào sau đây sai?
A. Phương trình vô nghiệm.
B. Phương trình có một nghiệm.
C. Nghiệm của phương trình lớn hơn 0.
D. Phương trình đã cho nghiệm:
Câu 3: Nghiệm của phương trình là A. . B. . C. . D. .
Câu 4:Nghiệm của phương trình là A. 10. B. 8. C. 11. D. 6. DẶN DÒ
1. Xem lại nội dung vừa học.
2. Xem nội dung Bất phương trình mũ & Bất phương trình lôgarit. THANK YOU FOR YOUR ATTENTION
Document Outline
- CHƯƠNG IV: HÀM SỐ MŨ & HÀM SỐ LÔGARIT
- VẬN DỤNG
- KHỞI ĐỘNG
- HOẠT ĐỘNG 1
- HOẠT ĐỘNG 1
- I. PHƯƠNG TRÌNH MŨ
- Hình vẽ hoạt động 2
- Slide 8
- I. PHƯƠNG TRÌNH MŨ
- Ví dụ 2.
- Ví dụ 2:
- Cách giải phương trình mũ cơ bản
- Ví dụ 2:
- Ví dụ 3: Hoạt động 1 đầu bài.
- HOẠT ĐỘNG 3
- II. PHƯƠNG TRÌNH LÔGARIT
- II. PHƯƠNG TRÌNH LÔGARIT
- HOẠT ĐỘNG 4
- Hình vẽ hoạt động 4
- II. PHƯƠNG TRÌNH LÔGARIT
- Cách giải phương trình logarit cơ bản
- Ví dụ 5.
- III.
- PHIẾU HỌC TẬP
- IV.
- VẬN DỤNG
- Slide 27
- Slide 28
- Slide 29
- Slide 30
- Slide 31
- DẶN DÒ
- THANK YOU FOR YOUR ATTENTION




