











Preview text:
CHÀO MỪNG CẢ LỚP
ĐẾN VỚI TIẾT HỌC HÔM NAY! KHỞI ĐỘNG
Trong Hình 1, hai đường thẳng gợi nên hình ảnh hai đường thẳng vuông góc trong không gian.
Trong không gian, thế nào là
hai đường thẳng vuông góc với nhau?
CHƯƠNG VIII. QUAN HỆ VUÔNG GÓC TRONG KHÔNG GIAN.
PHÉP CHIẾU VUÔNG GÓC
BÀI 1. HAI ĐƯỜNG THẲNG VUÔNG GÓC NỘI DUNG BÀI HỌC
Góc giữa hai đường thẳng I trong không gian II
Hai đường thẳng vuông góc trong không gian I
GÓC GIỮA HAI ĐƯỜNG THẲNG TRONG KHÔNG GIAN HĐ H Đ 1
Trong mặt phẳng cho hai đường thẳng .
a) Nếu và cắt nhau tại (Hình 2) thì góc giữa hai
đường thẳng được xác định như thế nào?
b) Nếu thì góc giữa và bằng bao nhiêu độ?
c) Nếu và trùng nhau thì góc giữa và bằng bao nhiêu độ? Giải
a) Nếu và cắt nhau tại thì góc giữa hai đường thẳng được xác định bằng góc
giữa hai tia đi qua và tạo thành hai đường thẳng đó.
b) Nếu thì hai đường thẳng và không có điểm chung, do đó
không có góc tạo bởi và . HĐ H Đ 1
Trong mặt phẳng cho hai đường thẳng .
a) Nếu và cắt nhau tại (Hình 2) thì góc giữa hai
đường thẳng được xác định như thế nào?
b) Nếu thì góc giữa và bằng bao nhiêu độ?
c) Nếu và trùng nhau thì góc giữa và bằng bao nhiêu độ? Giải
c) Nếu và trùng nhau thì hai đường thẳng và không có điểm cắt nào nên góc
giữa hai đường thẳng này không xác định. Kết luận
Góc giữa hai đường thẳng và trong không gian là góc
giữa hai đường thẳng và cùng đi qua một điểm và lần
lượt song song (hoặc trùng) với và , kí hiệu hoặc . Nhận xét:
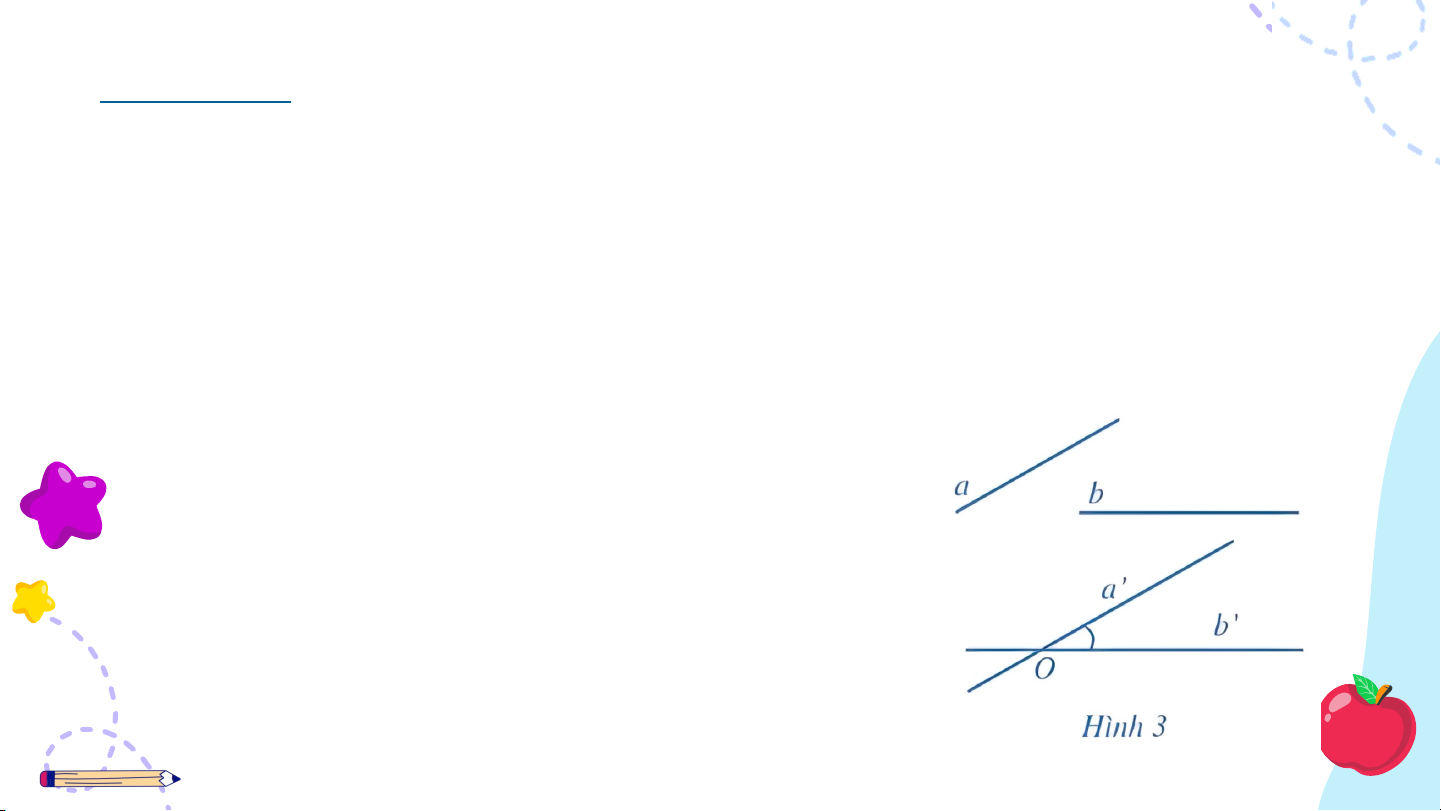
• Góc giữa hai đường thẳng không phụ thuộc vào vị trí điểm (Hình 3).
Thông thường, khi tìm góc giữa hai đường thẳng , ta chọn thuộc hoặc thuộc .
• Góc giữa hai đường thẳng bằng góc giữa hai đường thẳng tức là .
• Góc giữa hai đường thẳng không vượt quá .
• Nếu thì với mọi đường thẳng trong không gian.
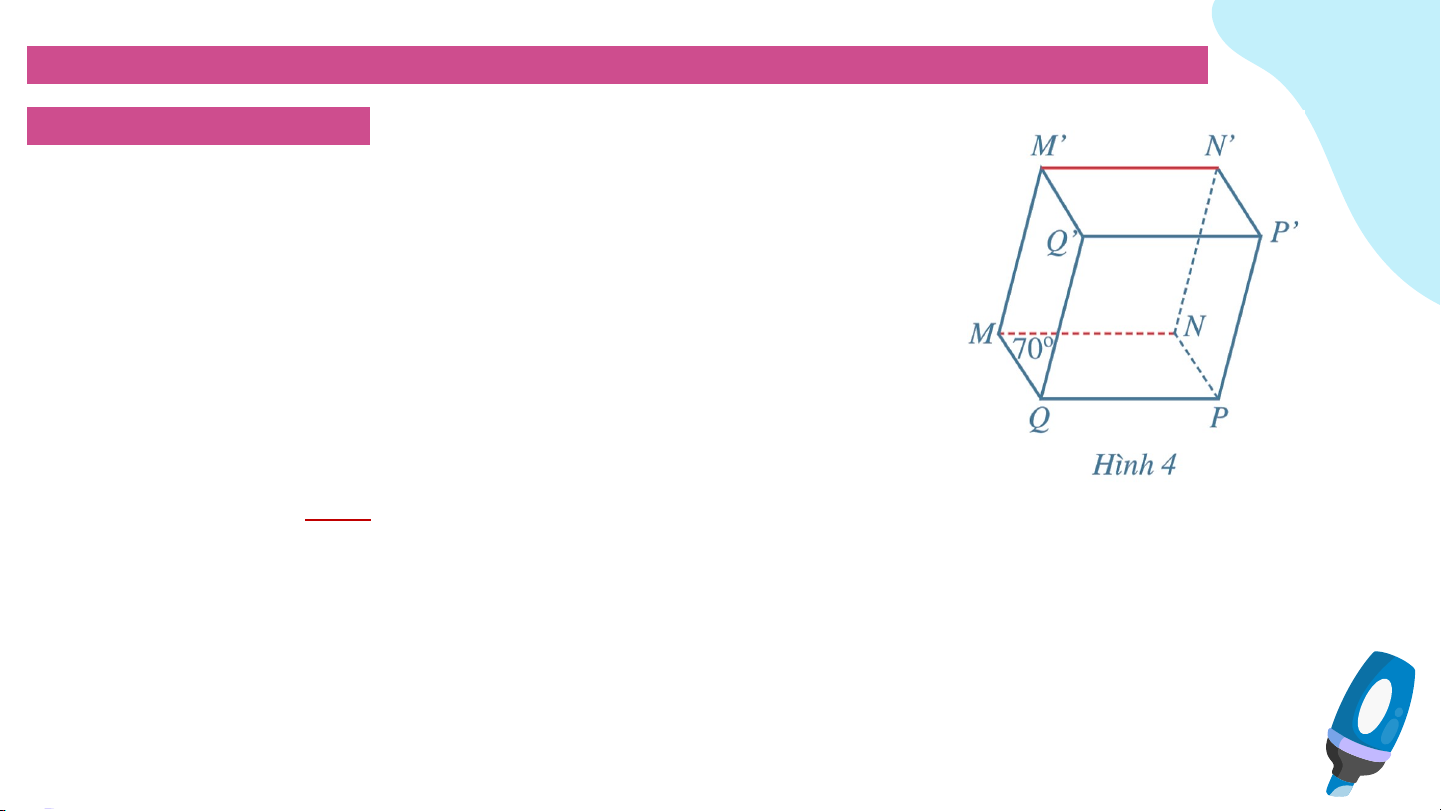
Ví dụ 1: Cho hình hộp MNPQ.M’N’P’Q có góc giữa hai đường thẳng MN và MQ bằng 70° (Hình 4).
a) Góc giữa hai đường thẳng M’N’ và NP bằng góc giữa hai đường thẳng: A. MN và MP. B. MN và MQ. C. MP và NP. D. NN’ và NP.
b) Tính góc giữa hai đường thẳng M’N và NP. Giải
a) Vì M’N’ // MN, NP // MQ nên góc giữa hai đường thẳng M’N’ và NP bằng góc giữa
hai đường thẳng MN và MQ. Chọn phương án B.
b) Vì góc giữa hai đường thẳng MN và MQ bằng 70° nên góc giữa hai đường thẳng M’N’ và NP bằng 70°. Luyện tập 1
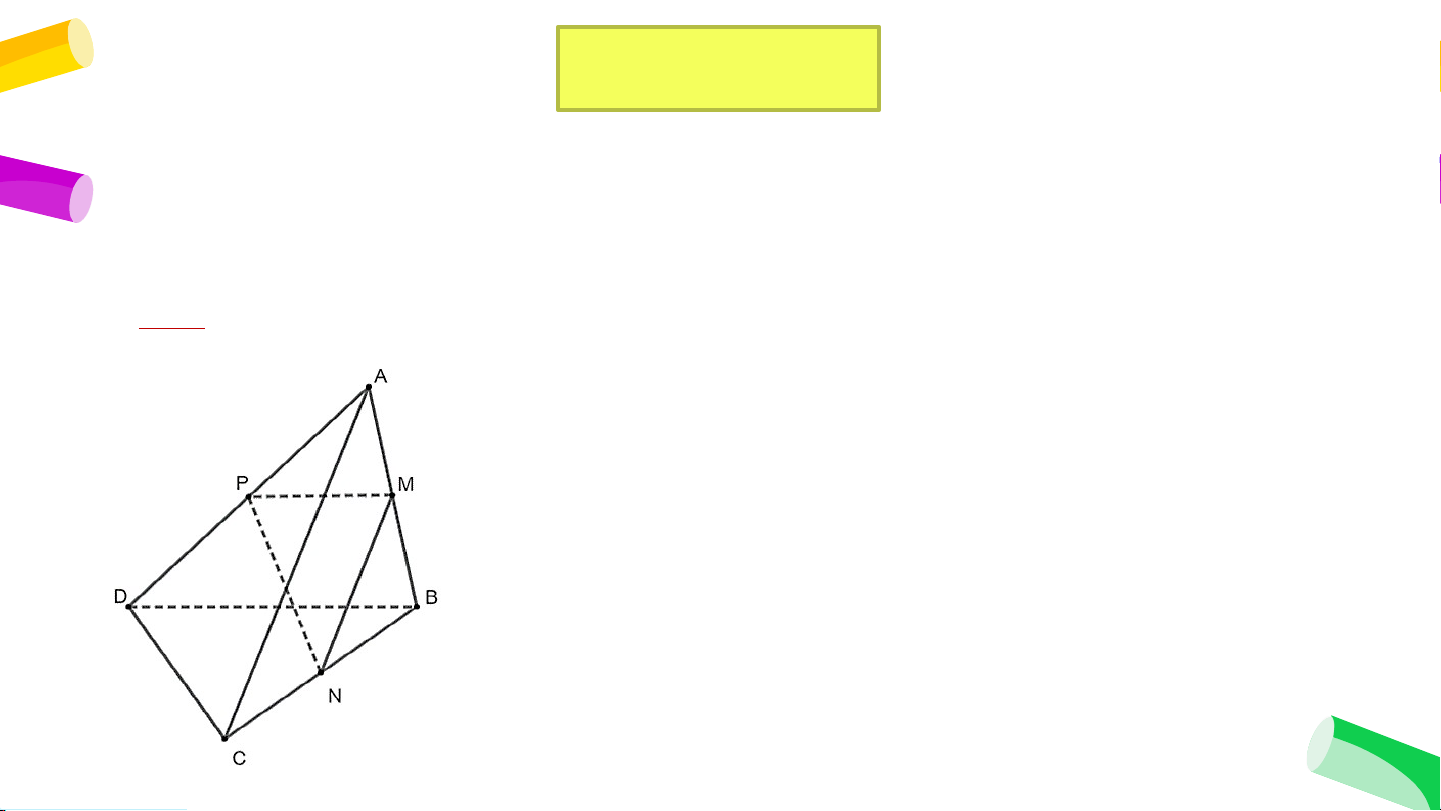
Cho tứ diện ABCD có M, N, P lần lượt là trung điểm của AB, BC, DA. Biết tam
giác MNP đều. Tính góc giữa hai đường thẳng AC và BD. Giải Xét có:
là đường trung bình của Xét có:
là đường trung bình của Ta có: đều nên II
HAI ĐƯỜNG THẲNG VUÔNG GÓC TRONG KHÔNG GIAN HĐ H Đ 2
Trong Hình 1 ở phần mở đầu, hai đường thẳng gợi nên
hình ảnh hai đường thẳng vuông góc. Góc giữa và bằng bao nhiêu độ? Góc giữa và bằng . LUYỆN TẬP Bắn Cung Tên
Câu 1. Cho tứ diện đều (Tứ diện có tất cả các cạnh bằng nhau).
Số đo góc giữa hai đường thẳng và bằng Đúng rồi Sai rồi 90𝑜 30𝑜 Sai rồi Sai rồi 45𝑜 60𝑜
Document Outline
- Slide 1
- Slide 2
- Slide 3
- II
- I
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- II
- Slide 13
- Slide 14
- Slide 15
- Slide 16




