









Preview text:
CHÀO MỪNG CÁC EM
ĐẾN VỚI TIẾT HỌC! KHỞI ĐỘNG
Trong Hình 9, cột gỗ thẳng đứng và
sàn nhà nằm ngang gợi nên hình
ảnh đường thẳng vuông góc với mặt phẳng.
Đường thẳng vuông góc với mặt
phẳng được hiểu như thế nào?
CHƯƠNG VIII. QUAN HỆ VUÔNG GÓC TRONG KHÔNG GIAN.
PHÉP CHIẾU VUÔNG GÓC
BÀI 2. ĐƯỜNG THẲNG VUÔNG GÓC VỚI MẶT PHẲNG NỘI DUNG BÀI HỌC I Định nghiã
Điều kiện để đường thẳng
II vuông góc với mặt phẳng III
Liên hệ giữa quan hệ song Tính chất
IV song và quan hệ vuông góc
của đường thẳng và mặt phẳng Phép chiếu V vuông góc
VI Định lí ba đường vuông góc I ĐỊNH NGHĨA
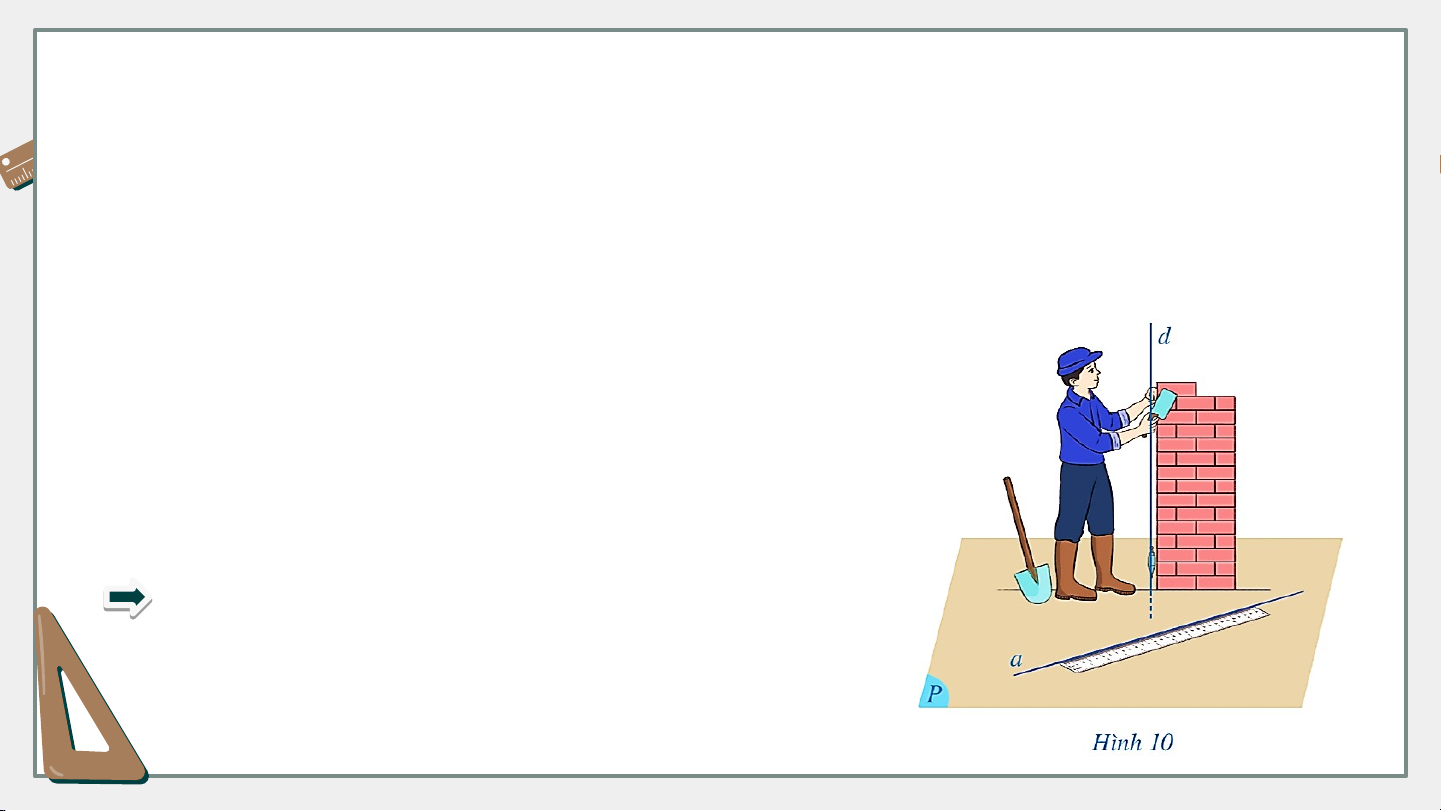
HĐ1: Hình 10 mô tả một người thợ xây đang thả dây dọi vuông góc với nền
nhà. Coi dây dọi như đường thẳng và nền nhà như mặt phẳng , khi đó Hình
10 gợi nên hình ảnh đường thẳng vuông góc với mặt phẳng . Người thợ xây
đặt chiếc thước thẳng ở một vị trí tùy ý trên nền nhà.
Coi chiếc thước thẳng đó là đường thẳng trong
mặt phẳng , nêu dự đoán về mối liên hệ giữa
đường thẳng và đường thẳng .
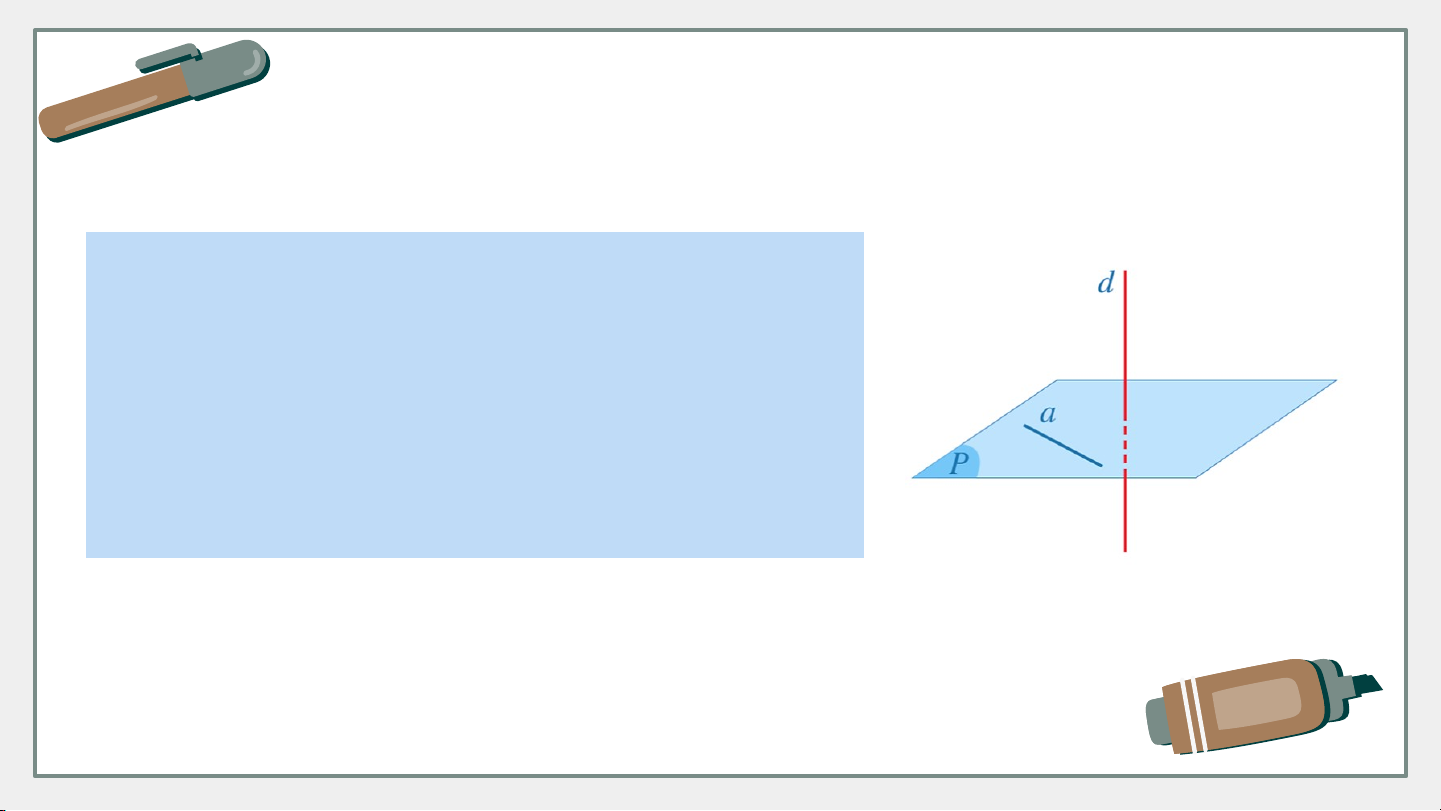
Dự đoán: Đường thẳng và đường thẳng vuông góc với nhau. KẾT LUẬN
Đường thẳng được gọi là vuông góc
với mặt phẳng nếu đường thẳng
vuông góc với mọi đường thẳng trong
mặt phẳng , kí hiệu hoặc . II
ĐIỀU KIỆN ĐỂ ĐƯỜNG THẲNG
VUÔNG GÓC VỚI MẶT PHẲNG HĐ2
Hình 12 mô tả cửa tròn xoay, ở đó trục cửa
và hai mép cửa gợi nên hình ảnh các đường
thẳng ; sàn nhà coi như mặt phẳng chứa
và . Hỏi đường thẳng có vuông góc với mặt phẳng hay không?
Ta thấy để cửa tròn xoay được trên mặt đất thì trục cửa
phải vuông góc với mặt đất. Vậy Định lí
Nếu một đường thẳng vuông góc với hai đường thẳng
cắt nhau cùng thuộc một mặt phẳng thì nó vuông góc với mặt phẳng ấy.
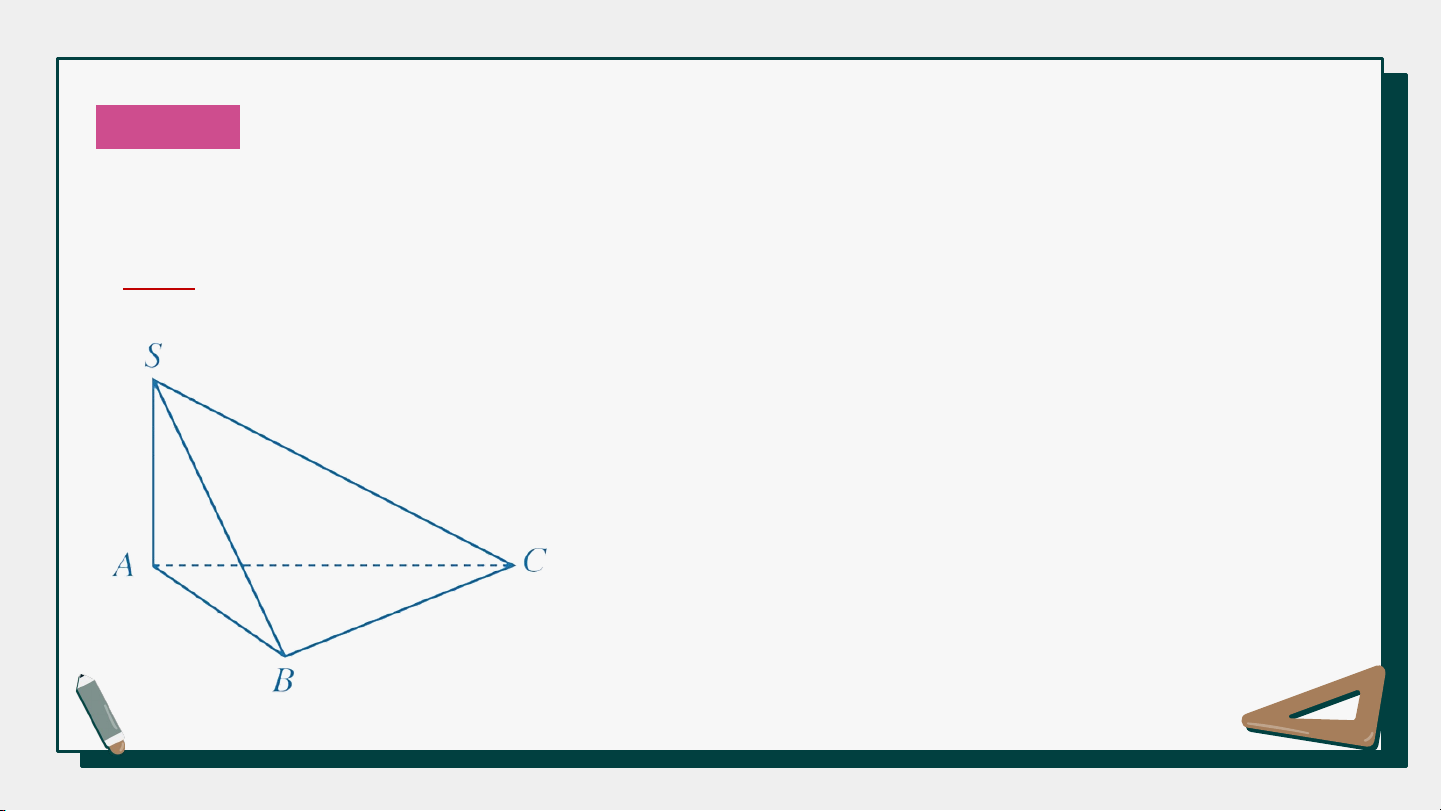
Ví dụ 1: Cho hình chóp S.ABC có SA AB, SA AC. Chứng minh rằng SA (ABC) và SA BC. Giải
Ta có AB và AC là hai đường thẳng cắt
nhau trong mặt phẳng (ABC) và SA AB, SA AC. Suy ra SA (ABC). Mà BC (ABC) nên SA BC.
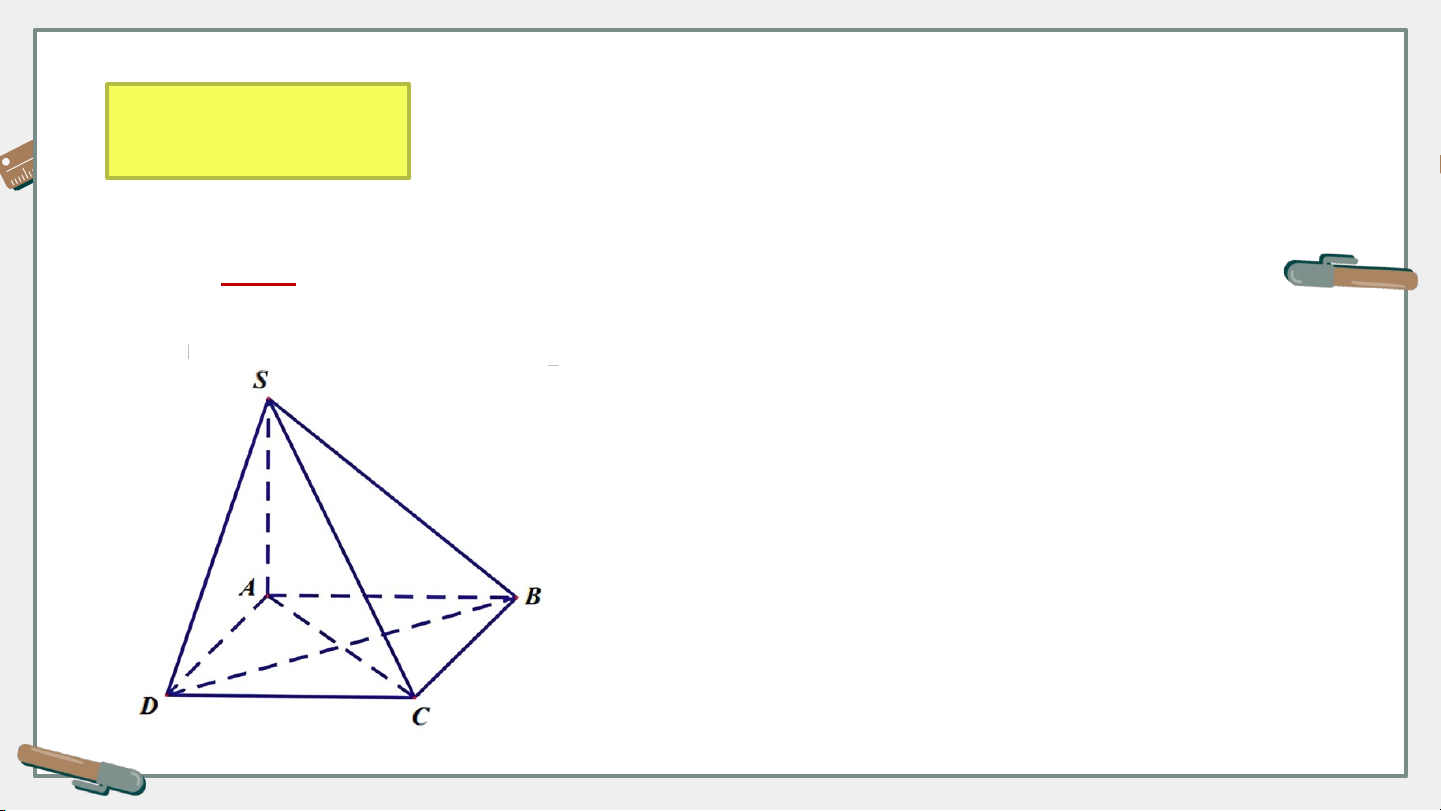
Cho hình chóp có đáy là hình thoi, Luyện tập 1 . Chứng minh rằng . Giải Vì Vì là hình thoi Xét và có: . III TÍNH CHẤT
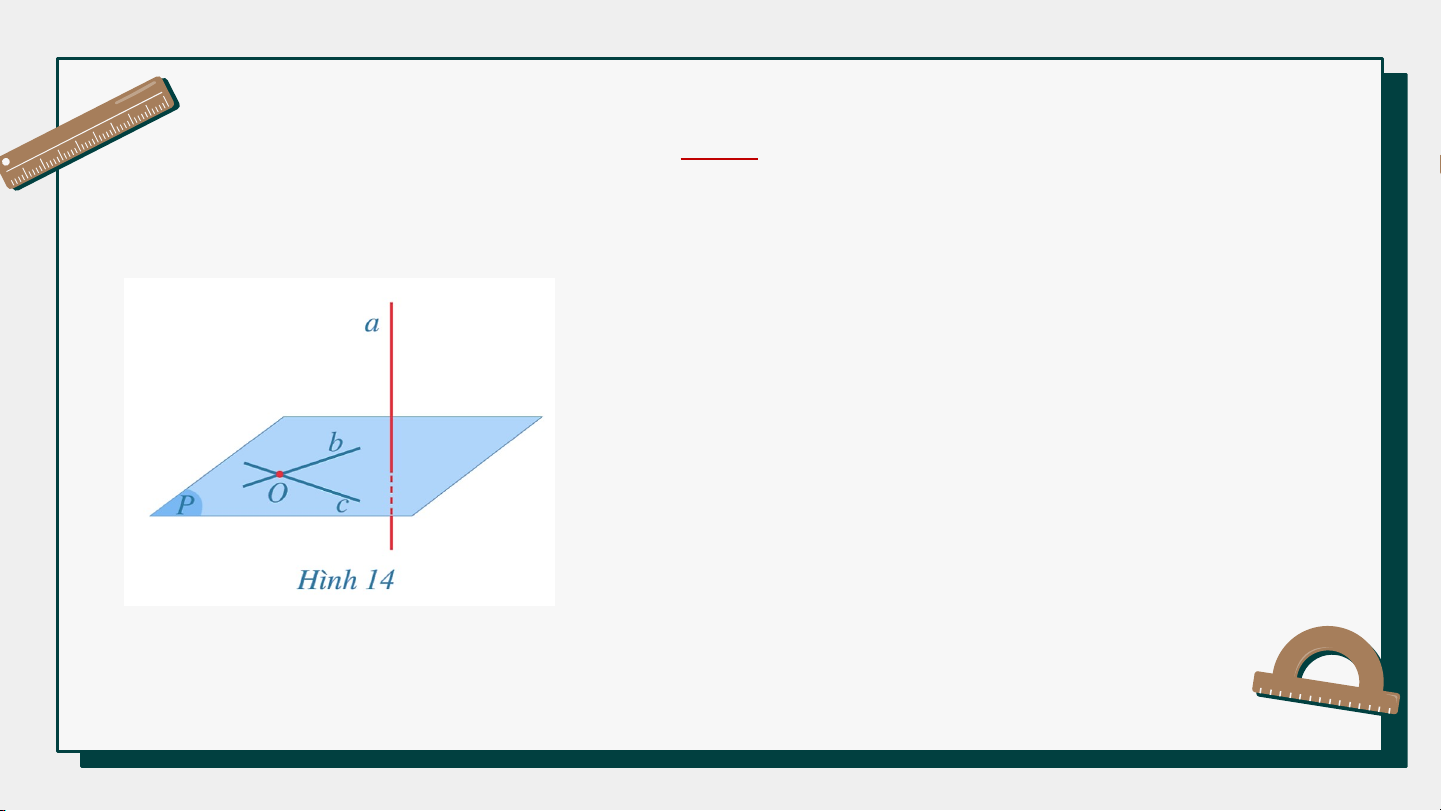
HĐ3: Cho điểm và đường thẳng . Gọi
là hai đường thẳng phân biệt cùng đi
qua điểm và cùng vuông góc với đường thẳng (Hình 14).
a) Mặt phẳng đi qua hai đường thẳng có vuông góc với đường thẳng hay không?
b) Có bao nhiêu mặt phẳng đi qua điểm và vuông góc với đường thẳng ? Giải a) Ta có:
b) Chỉ có một mặt phẳng duy nhất đi
qua điểm và vuông góc với . Tính chất 1
Có duy nhất một mặt phẳng đi qua một điểm
cho trước và vuông góc với một đường thẳng cho trước.
Câu 1. Khẳng định nào sau đây sai?
B. Nếu đường thẳng vuông góc với
A. Nếu đường thẳng thì vuông góc với
hai đường thẳng nằm trong thì . hai đường thẳng trong .
C. Nếu đường thẳng vuông góc với hai
D. Nếu và đường thẳng thì .
đường thẳng cắt nhau nằm trong thì
vuông góc với bất kì đường thẳng nào nằm trong .
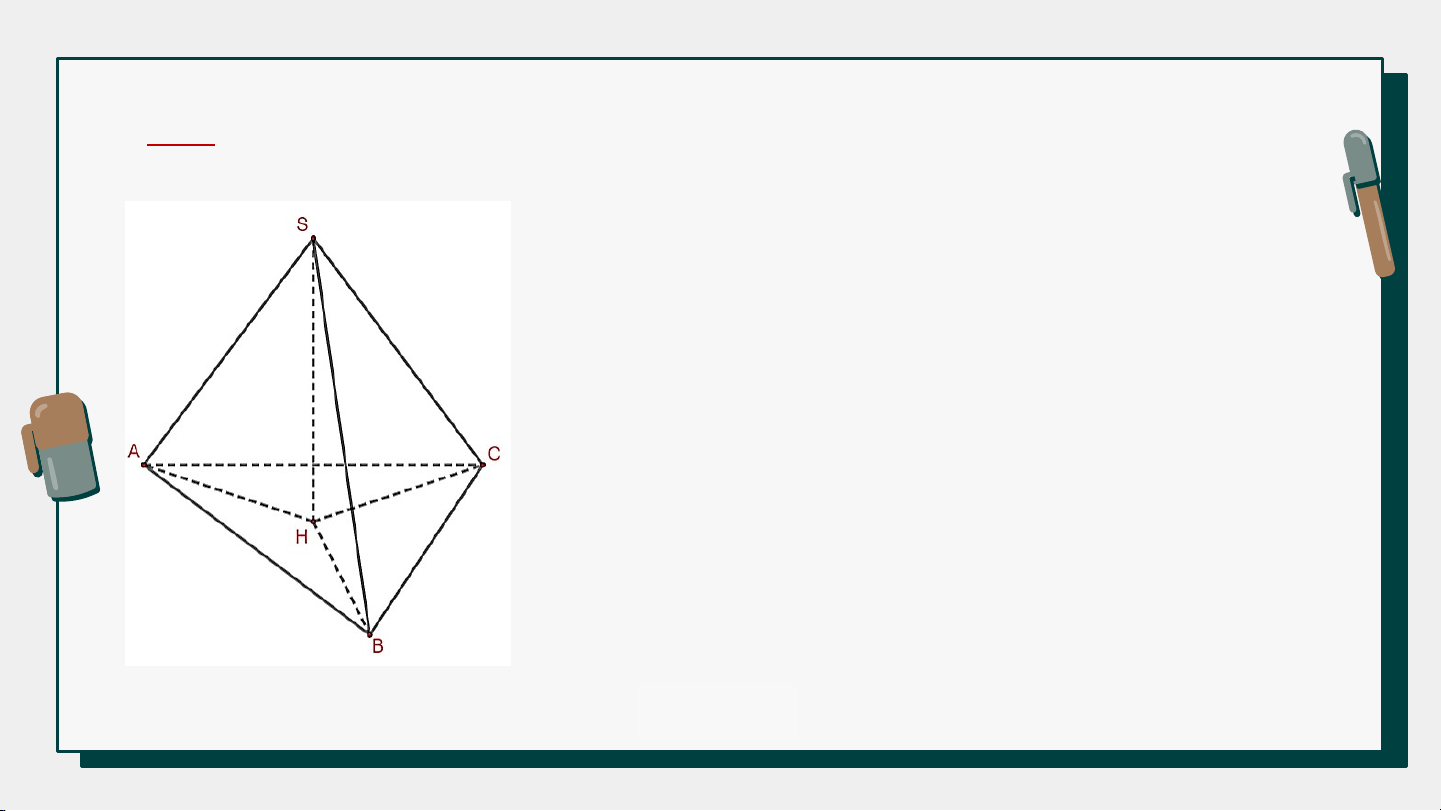
Câu 2. Cho hình chóp có và tam giác vuông tại . Vẽ , . Khẳng định nào sau đây đúng?
A. H trùng với trọng tâm tam giác
B. H trùng với trực tâm tam giác ABC. ABC.
C. H trùng với trung điểm của AC.
D. H trùng với trung điểm của BC. Giải Tương tự: (2) Từ (1)(2) là trực tâm , mà . VẬN DỤNG Bài 3 (SGK – tr.88)
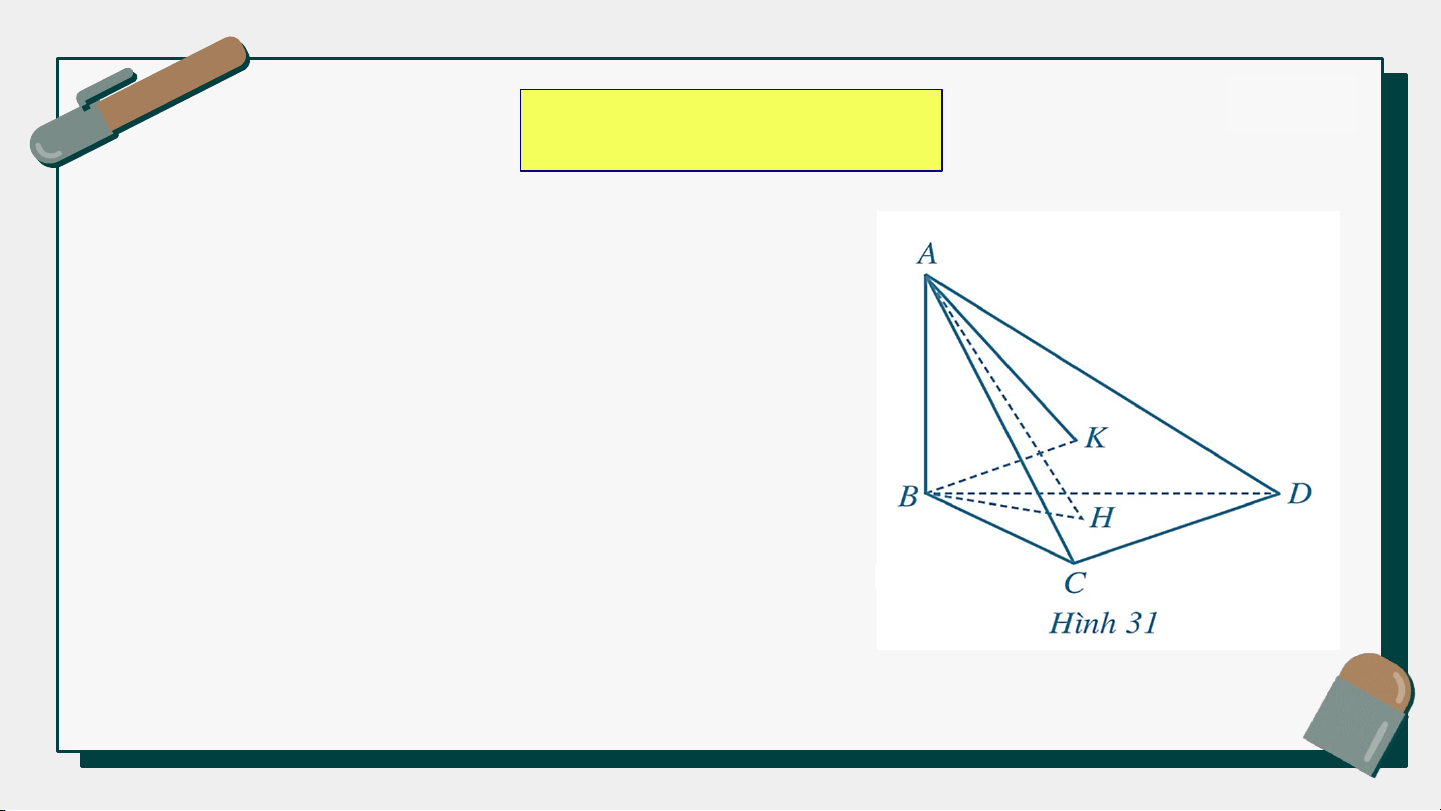
Cho tứ diện ABCD có AB ⊥ (BCD) các
tam giác BCD và ACD là những tam giác
nhọn. Gọi H, K lần lượt là trực tâm của
các tam giác BCD, ACD (Hình 31). Chứng minh rằng: a) CD ⊥ (ABH); b) CD ⊥ (ABK);
c) Ba đường thẳng AK, BH, CD cùng đi qua một điểm.
Document Outline
- Slide 1
- KHỞI ĐỘNG
- Slide 3
- VI
- I
- Slide 6
- Slide 7
- II
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- III
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- VẬN DỤNG
- Slide 22




