Giáo án điện tử Toán 11 Chương 8 Bài 3 Cánh diều: Góc giữa đường thẳng và mặt phẳng. Góc nhị diện

CHÀO MỪNG CÁC EM
ĐÃ ĐẾN VỚI BUỔI HỌC! KHỞI ĐỘNG
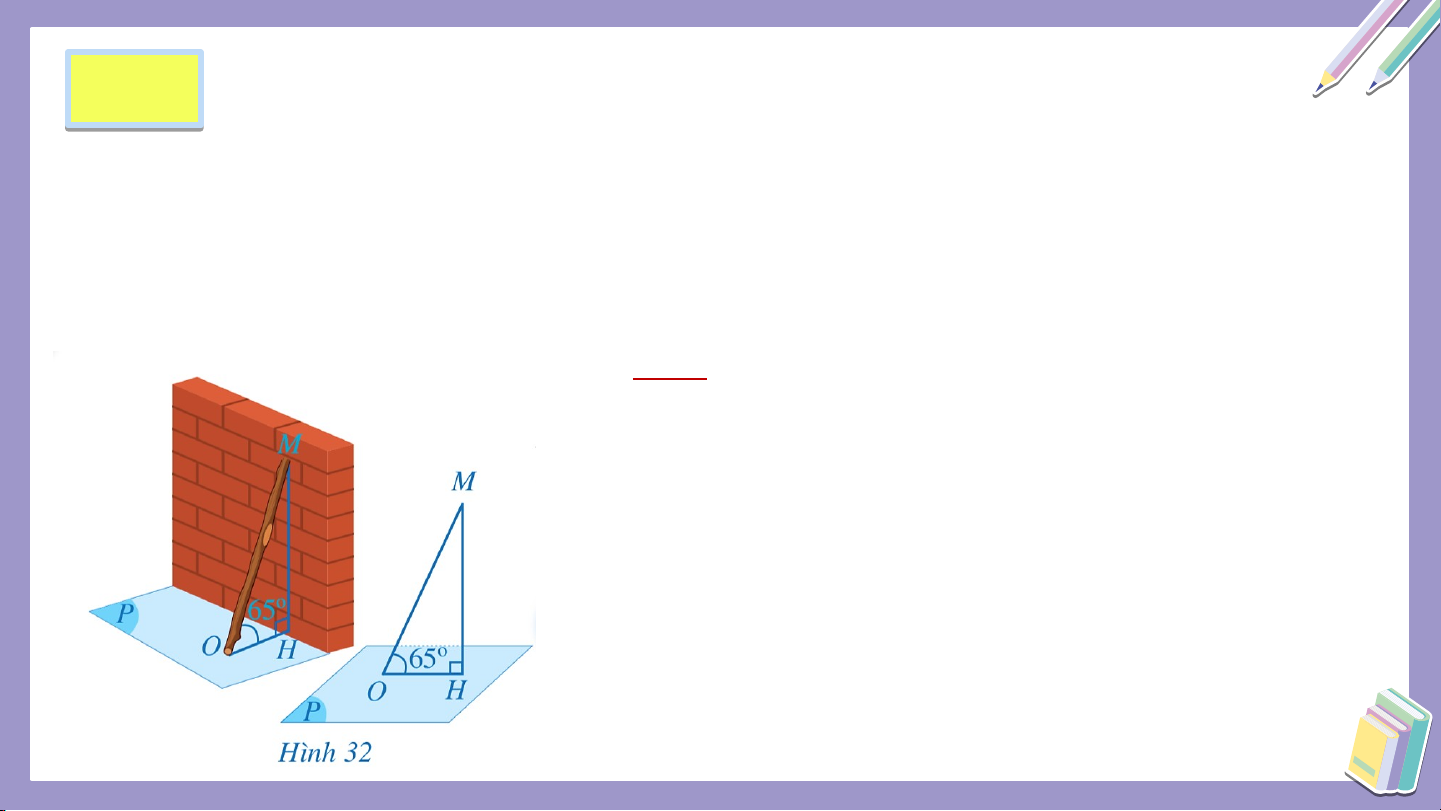
Hình 32 biểu diễn một chiếc gậy dựa
vào tường. Bạn Hoa nói góc nghiêng
giữa chiếc gậy và mặt đất bằng .
Góc nghiêng giữa chiếc gậy
và mặt đất được hiểu như thế nào?
CHƯƠNG VIII. QUAN HỆ
VUÔNG GÓC TRONG KHÔNG GIAN.
PHÉP CHIẾU VUÔNG GÓC
BÀI 3. GÓC GIỮA ĐƯỜNG THẲNG
VÀ MẶT PHẲNG. GÓC NHỊ DIỆN NỘI DUNG BÀI HỌC I
Góc giữa đường thẳng và mặt phẳng III Góc nhị diện
I. GÓC GIỮA ĐƯỜNG THẲNG VÀ MẶT PHẲNG HĐ H
Đ 1 Quan sát Hình 32 và cho biết:
a) Hình chiếu của đường thẳng trên mặt phẳng là đường thẳng nào;
b) Góc giữa đường thẳng và hình chiếu của đường thẳng đó trên Giải mặt phẳng là góc nào.
a) Vì nên hình chiếu của trên là .
b) Góc giữa đường thẳng và hình chiếu
của đường thẳng đó trên là . ĐỊNH NGHĨA
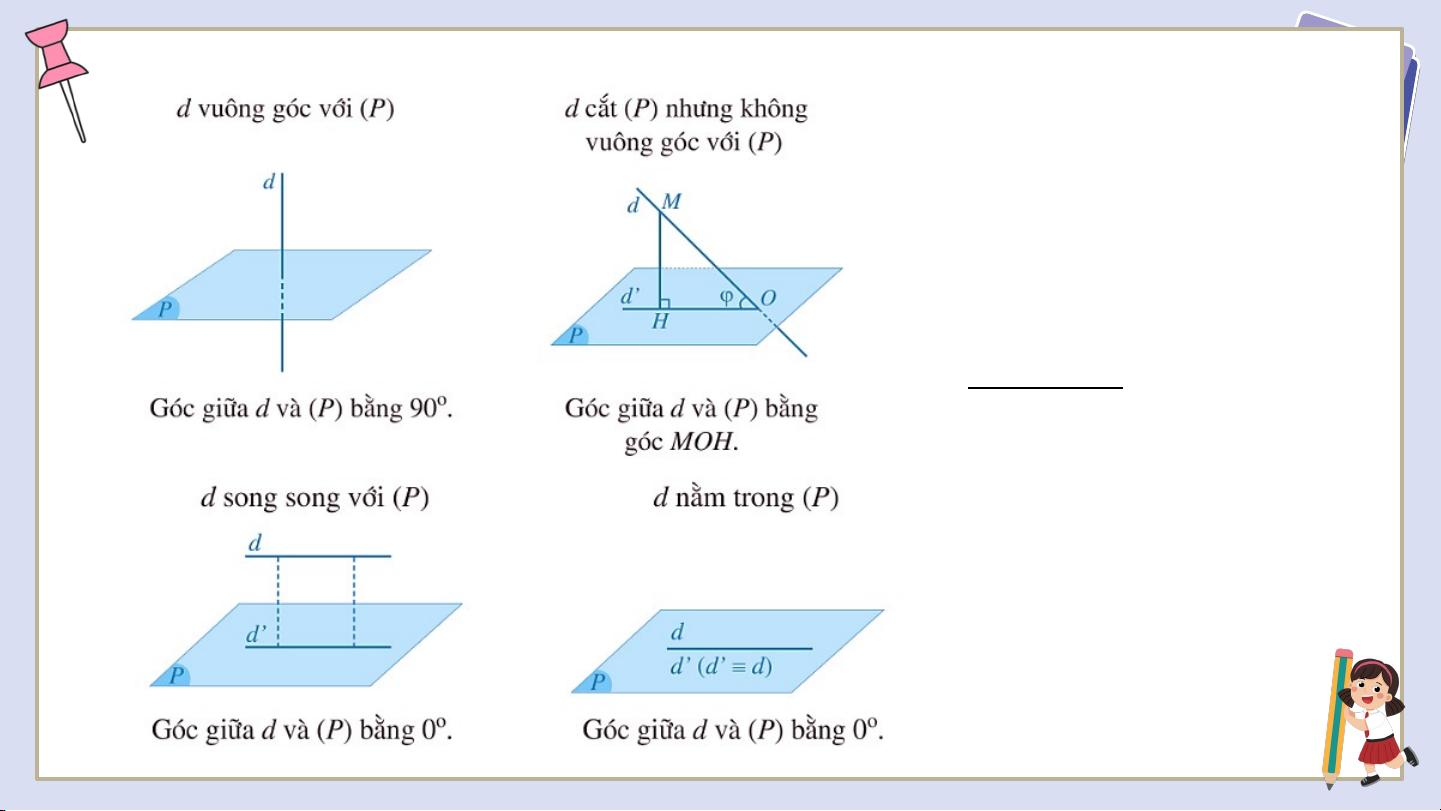
• Nếu đường thẳng vuông góc với mặt phẳng thì góc giữa đường thẳng và bằng .
• Nếu đường thẳng không vuông góc với mặt phẳng thì góc
giữa đường thẳng và mặt phẳng là góc giữa và hình chiếu
của đường thẳng trên . Nhận xét: Góc giữa đường thẳng
và mặt phẳng có số đo từ đến
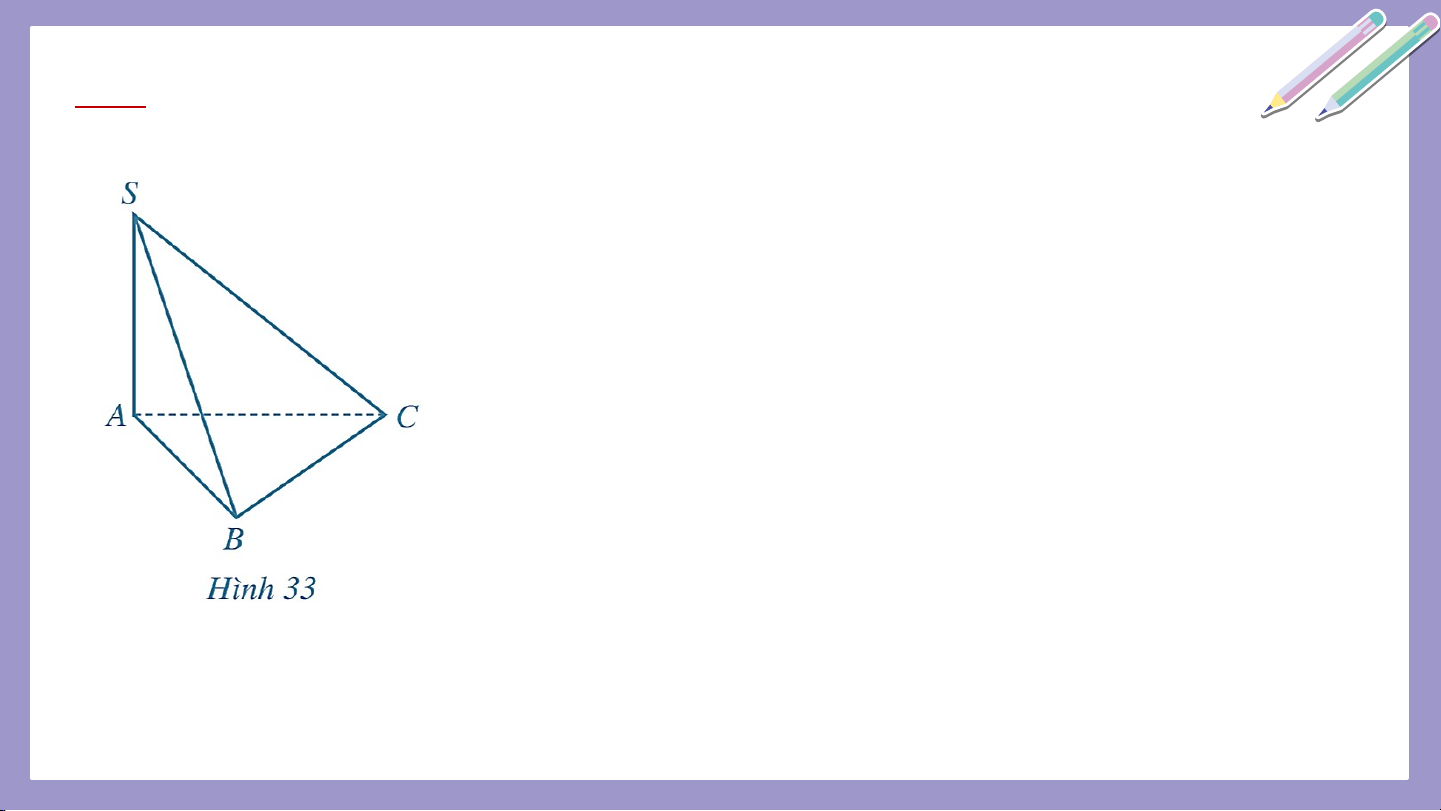
Ví dụ 1: Cho hình chóp có (Hình 33).
a) Tính góc giữa đường thẳng và mặt phẳng
b) Tính góc giữa đường thẳng và mặt phẳng biết Giải
a) Vì nên góc giữa đường thẳng và mặt phẳng bằng Giải
b) Vì nên là hình chiếu của trên
Suy ra góc giữa đường thẳng và mặt phẳng bằng . Xét tam giác vuông . Vì nên
Vậy góc giữa đường thẳng và mặt phẳng bằng .
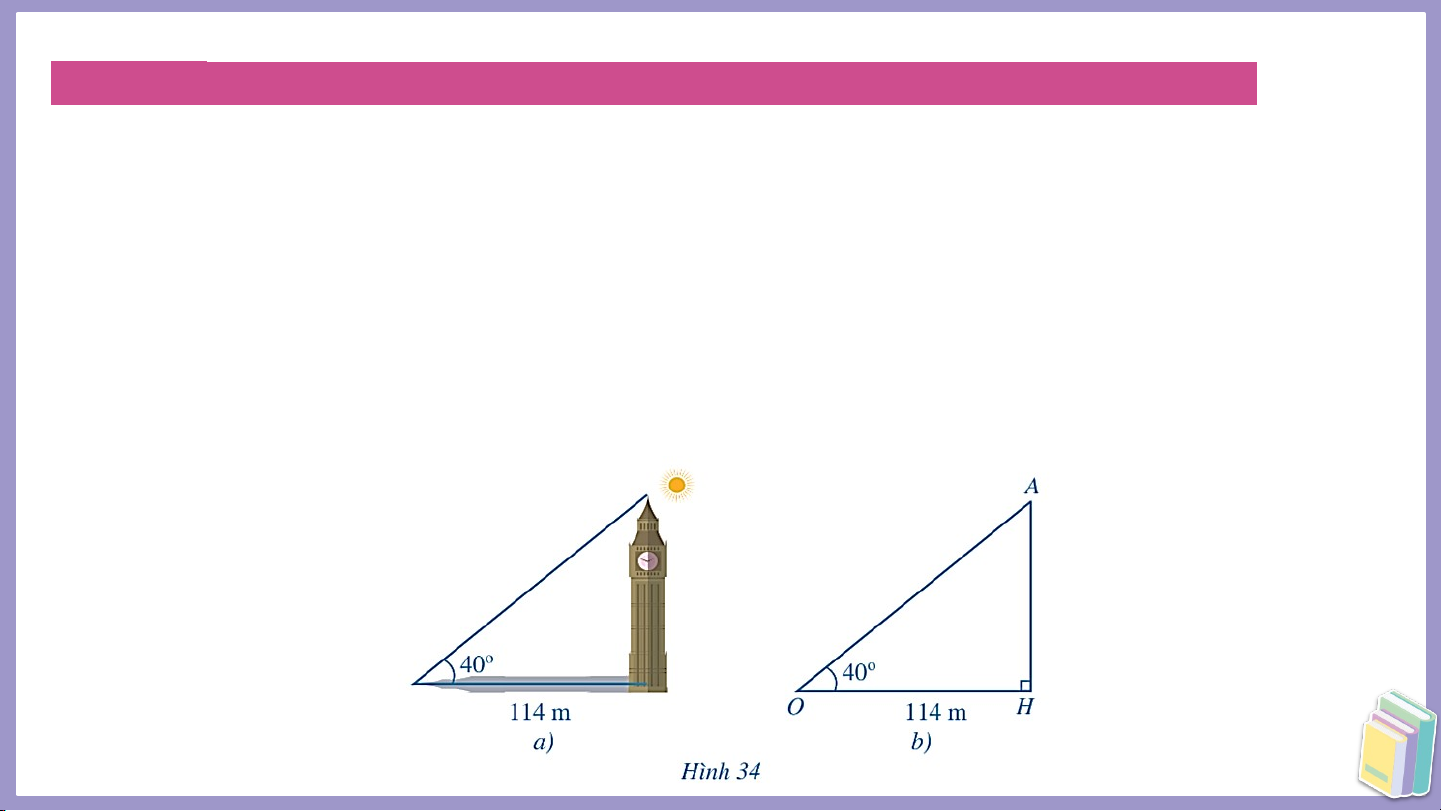
Ví dụ 2: Bài toán đo chiều cao của tháp khi không thể lên tới đỉnh tháp.
Để ước lượng chiều cao của tháp khi không thể lên tới đỉnh tháp, người ta đo
góc giữa tia nắng chiếu qua đỉnh tháp và mặt đất, đo chiều dài của bóng tháp
trên mặt đất, từ đó ước lượng được chiều cao của tháp. Giả sử khi tia nắng tạo
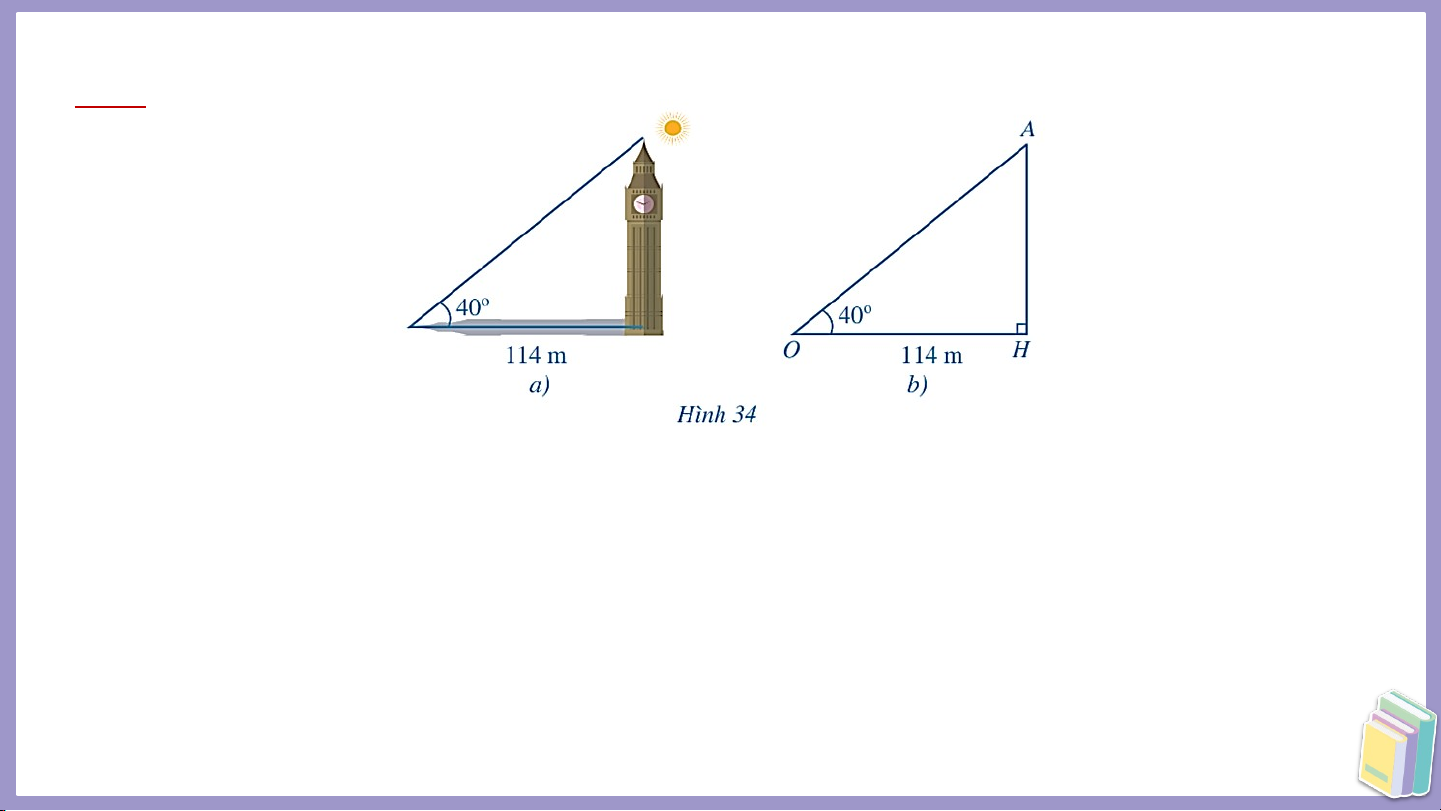
với mặt đất một góc 40°, chiều dài của bóng tháp là 114 m (Hình 34a). Tính
chiều cao của tháp theo đơn vị mét (làm tròn kết quả đến hàng phần mười). Giải
Xét Hình 34b, độ dài chỉ chiều cao của tháp, độ dài chỉ chiều dài của bóng
tháp, độ lớn của góc chỉ số đo góc giữa tia nắng và mặt đất. Vì tam giác vuông tại nên Luyện tập 1
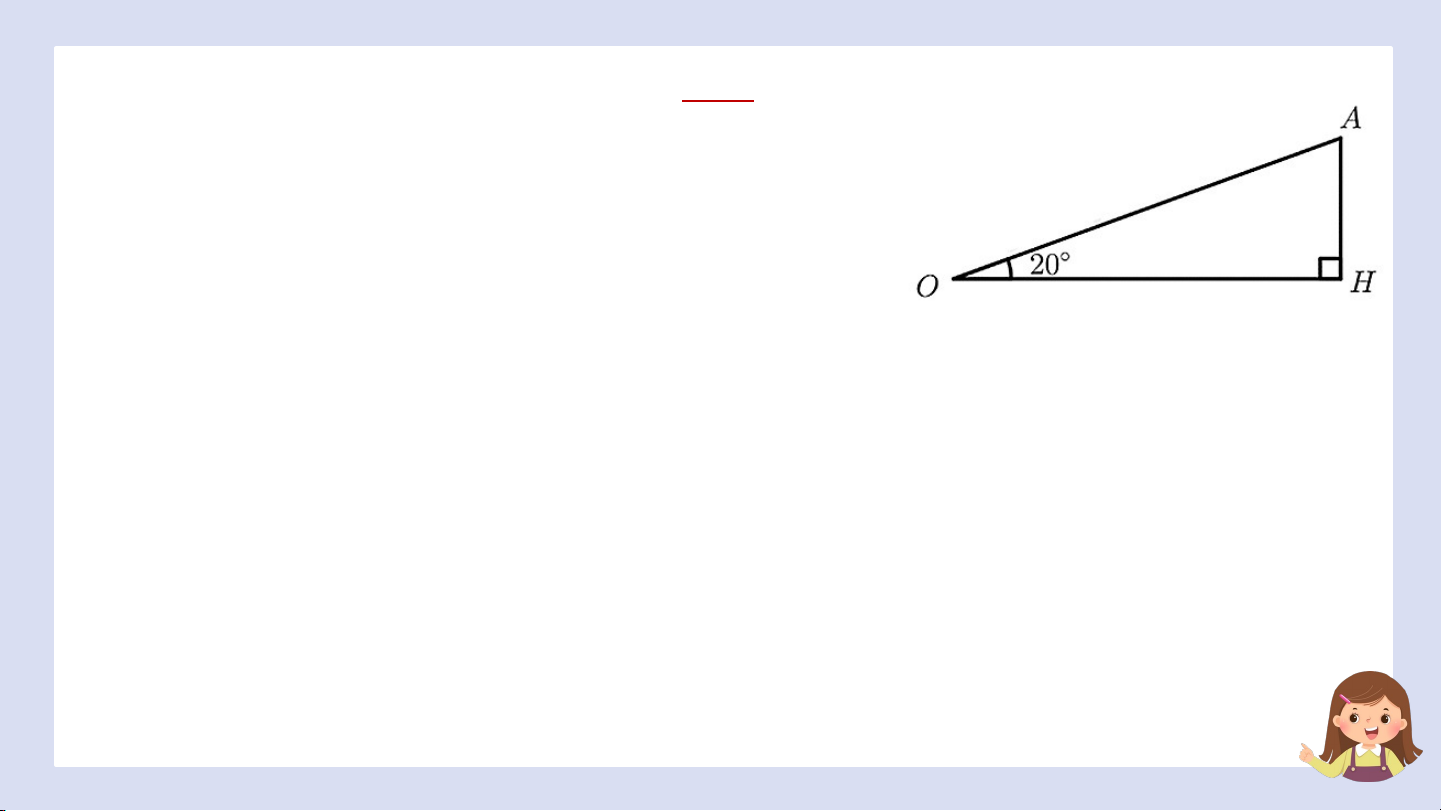
Giả sử ở những giây đầu tiên sau khi cất cánh, máy bay
chuyển động theo một đường thẳng tạo với mặt đất một
góc 20° và có vận tốc 200 km/h. Tính độ cao của máy bay
so với mặt đất theo đơn vị mét sau khi máy bay rời khỏi
mặt đất 2 giây (làm tròn kết quả đến hàng phần mười). Giải Đổi
Mô hình hóa như hình vẽ, với là quãng đường
máy bay bay được sau 2 giây, là độ cao của
máy bay so với mặt đất khi máy bay bay được
2 giây, độ lớn của là chỉ số đo góc giữa đường
thẳng máy bay bay và mặt đất.
Sau 2 giây máy bay bay được quãng đường là: (m) vuông tại nên ta có: (m) II. GÓC NHỊ DIỆN 1. K h K ái ái ni n ệm
Một đường thẳng nằm trong một mặt phẳng chia mặt
phẳng đó thành hai phần, mỗi phần được gọi là một
nửa mặt phẳng và đường thẳng đó được gọi là bờ của
mỗi nửa mặt phẳng này. HĐ 2 H
Quan sát hình ảnh một quyển sổ được mở ra (Hình 35),
mỗi trang sổ gợi nên hình ảnh của một nửa mặt phẳng.
Nêu đặc điểm của hai nửa mặt phẳng đó. Hai nửa mặt phẳng có chung bờ. KẾT LUẬN Góc n c hị d iện l à h ì h nh n g ồm ồ h ai a n ửa m ặt ặ p h p ẳng n c ó ó chung n b ờ.
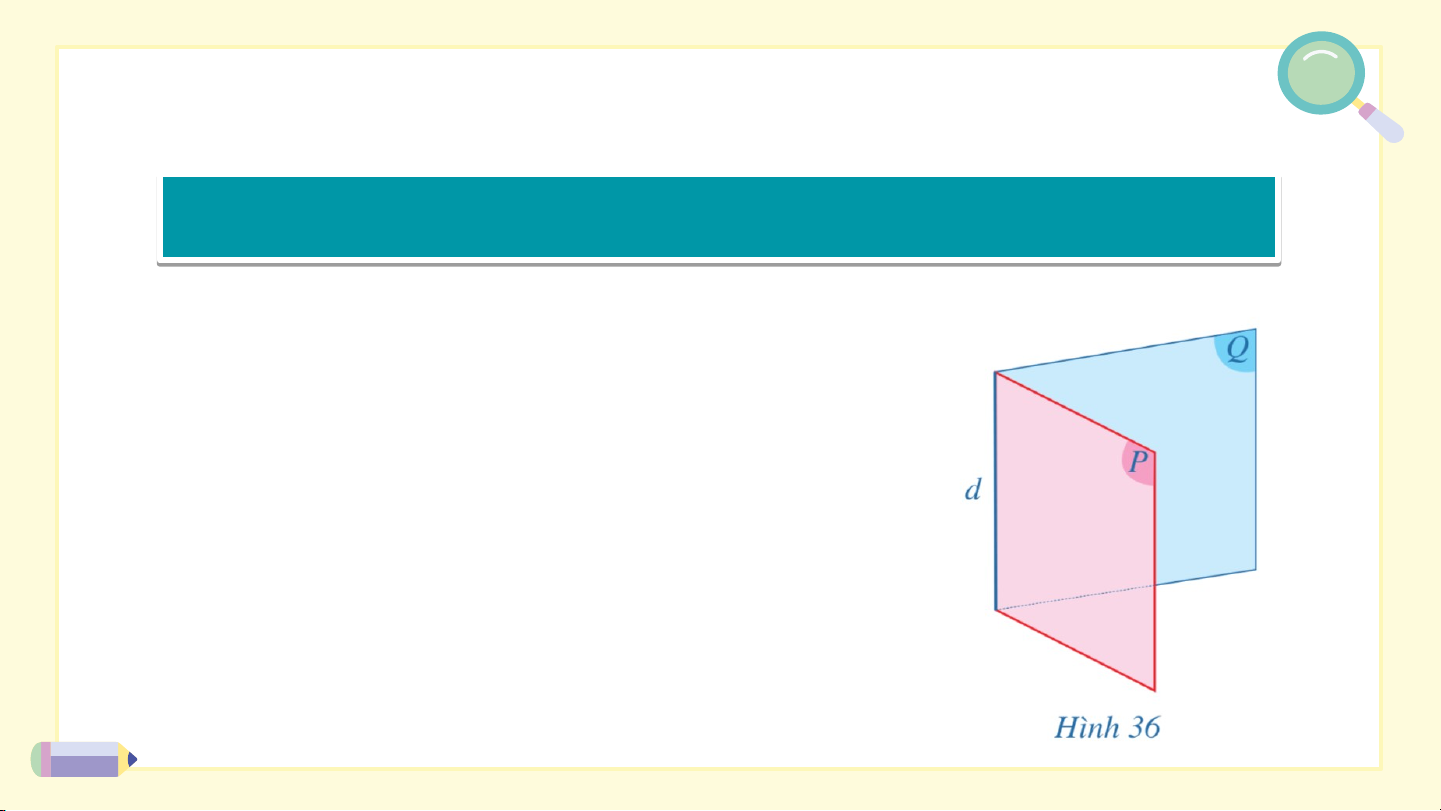
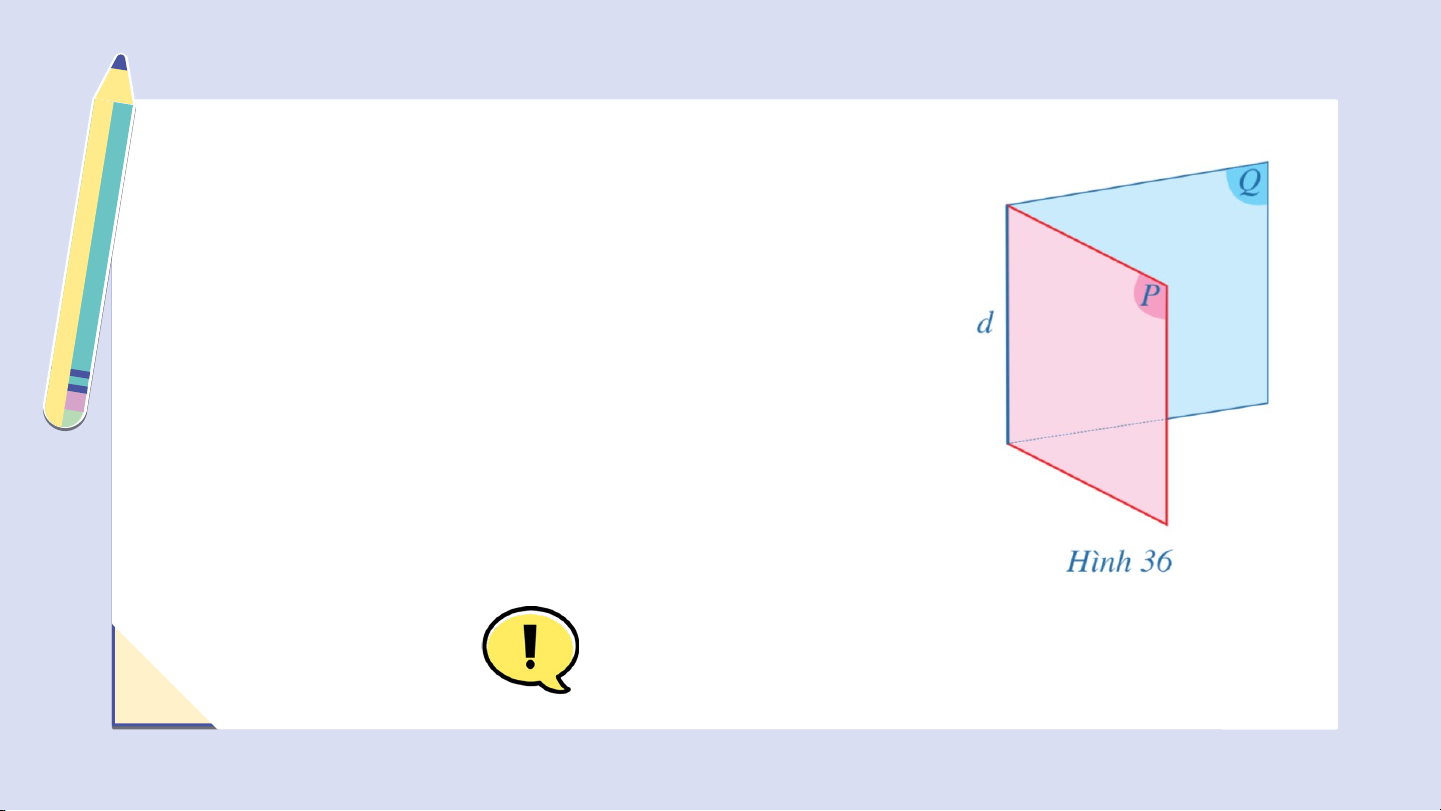
Trong Hình 36, ta có góc nhị diện gồm hai
nửa mặt phẳng và có chung bờ là
đường thẳng , kí hiệu là .
Đường thẳng gọi là cạnh của góc nhị
diện, mỗi nửa mặt phẳng và gọi là một mặt của góc nhị diện. Chú ý:
Góc nhị diện còn được kí hiệu là với
lần lượt là các điểm thuộc các nửa
mặt phẳng nhưng không thuộc đường thẳng .
Ví dụ 3: Trong không gian cho bốn nửa mặt phẳng (P), (Q), (R), (S)
cắt nhau theo giao tuyến d (Hình 37). Hãy chỉ ra ba góc nhị diện có
cạnh của góc nhị diện là đường thẳng d. Giải
Ba góc nhị diện có cạnh của góc nhị diện là
đường thẳng d, hai mặt lần lượt là:
(P) và (Q); (Q) và (R); (R) và (S). Luyện tập 2
Trong không gian cho hai mặt phẳng cắt nhau theo giao tuyến . Hai
mặt phẳng tạo nên bao nhiêu góc nhị diện có cạnh của góc nhị diện là đường thẳng ? Giải
Hai mặt phẳng và tạo nên 4 góc nhị diện có cạnh của góc nhị diện là đường thẳng . 2. S . ố S đ o củ o a củ gó g c ó n hị h d ị iệ i n H Đ H 3
Đ Cho góc nhị diện có hai mặt là hai nửa mặt phẳng
và cạnh của góc nhị diện là đường thẳng .
Qua một điểm trên đường thẳng , ta kẻ hai tia lần lượt
thuộc hai nửa mặt phẳng và cùng vuông góc với đường
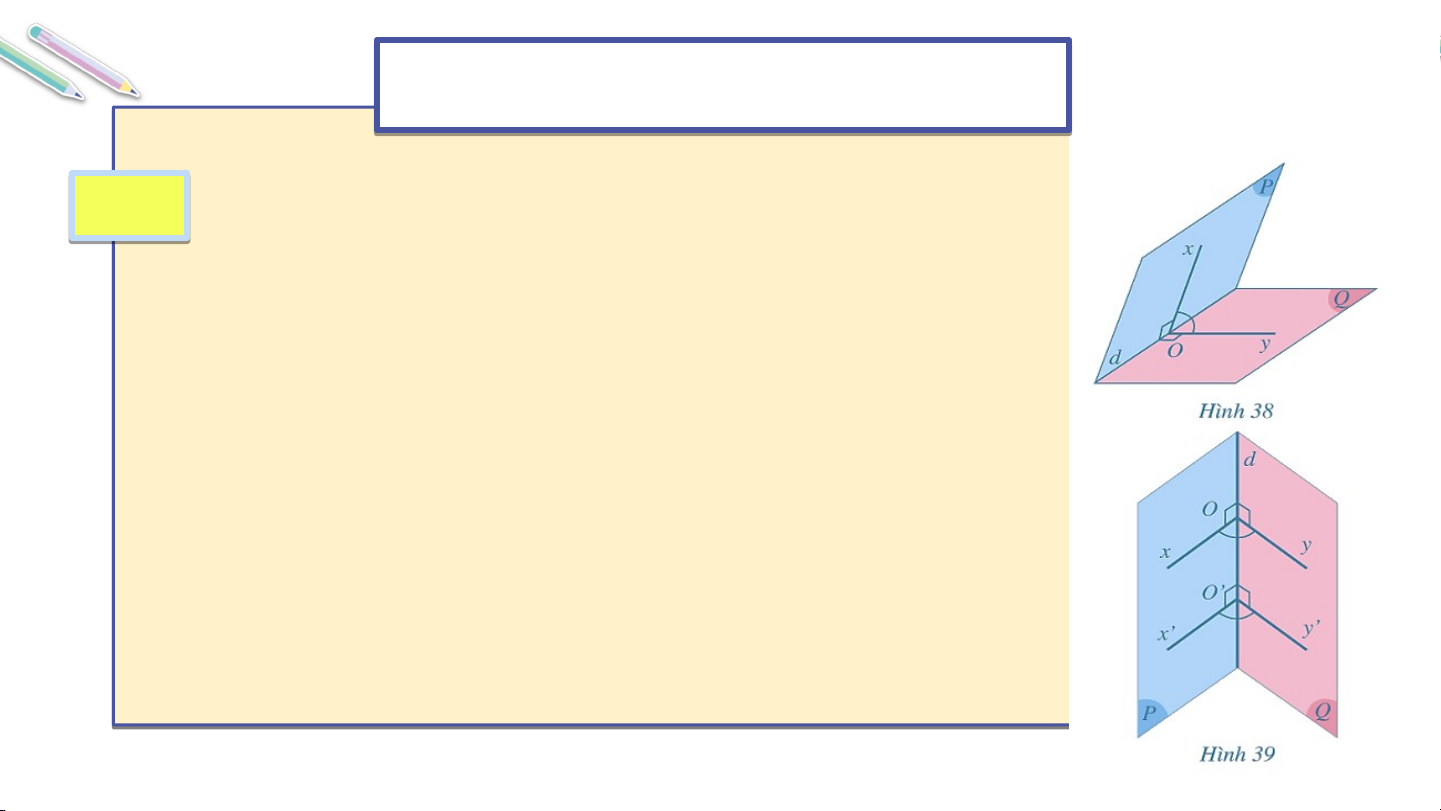
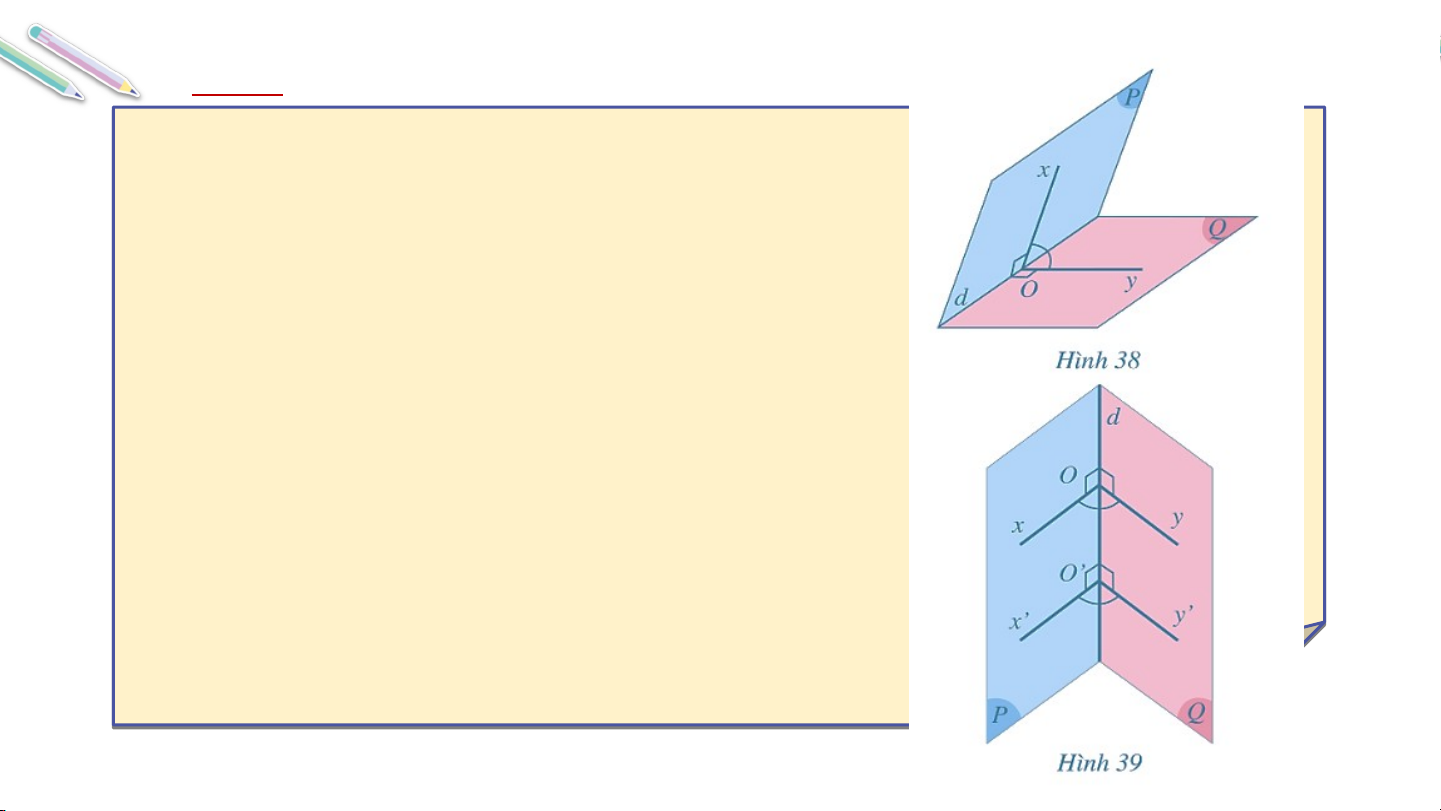
thẳng . Góc gọi là góc phẳng nhị diện của góc nhị diện đã cho (Hình 38).
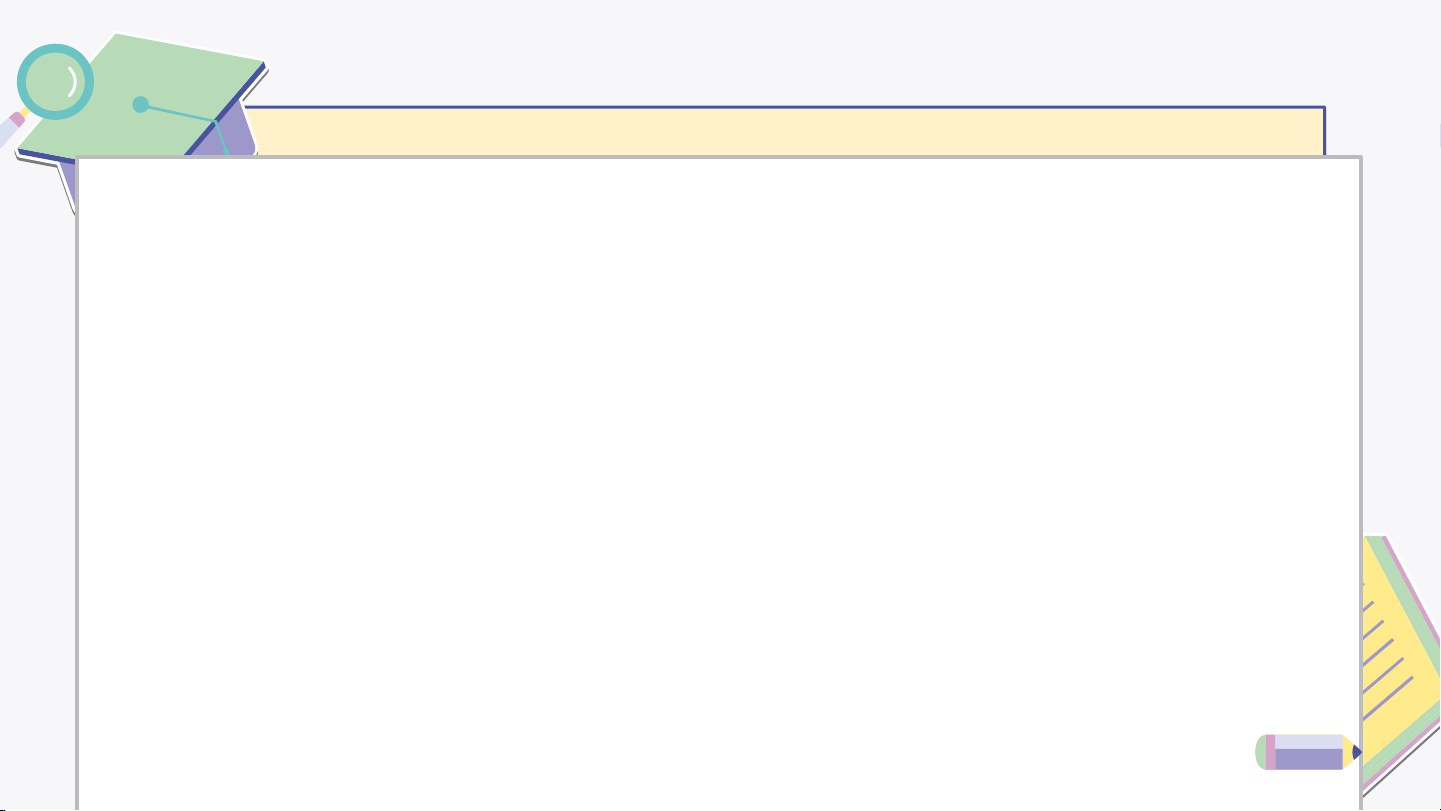
Giả sử góc cũng là góc phẳng nhị diện của góc nhị diện đã cho với khác (Hình 39).
Hãy so sánh số đo của hai góc và Giải Trong : Trong : Vậy hay số đo của . Nhận xét:
• Số đo góc phẳng nhị diện không phụ thuộc vào
vị trí của điểm trên cạnh nhị diện và được gọi
là số đo của góc nhị điện đã cho.
• Số đo của góc nhị diện từ đến . ĐỊNH NGHĨA
Trong không gian cho góc nhị diện.
• Một góc có đỉnh thuộc cạnh của góc nhị diện, hai cạnh của góc đó
lần lượt thuộc hai mặt nhị diện và cùng vuông góc với cạnh của
góc nhị diện được gọi là góc phẳng nhị diện của góc nhị diện đã cho.
• Số đo của một góc phẳng nhị điện được gọi là số đo của góc nhị diện đó.
• Nếu số đo góc phẳng nhị diện bằng thì góc nhị diện đó gọi là góc nhị diện vuông.
Ví dụ 4: Trong các công trình xây dựng nhà ở, độ dốc mái được hiểu là độ nghiêng của mái
khi hoàn thiện so với mặt phẳng nằm ngang. Khi thi công, mái nhà cần một độ nghiêng nhất
định để đảm bảo thoát nước tốt tránh gây ra tình trạng đọng nước hay thấm dột. Quan sát
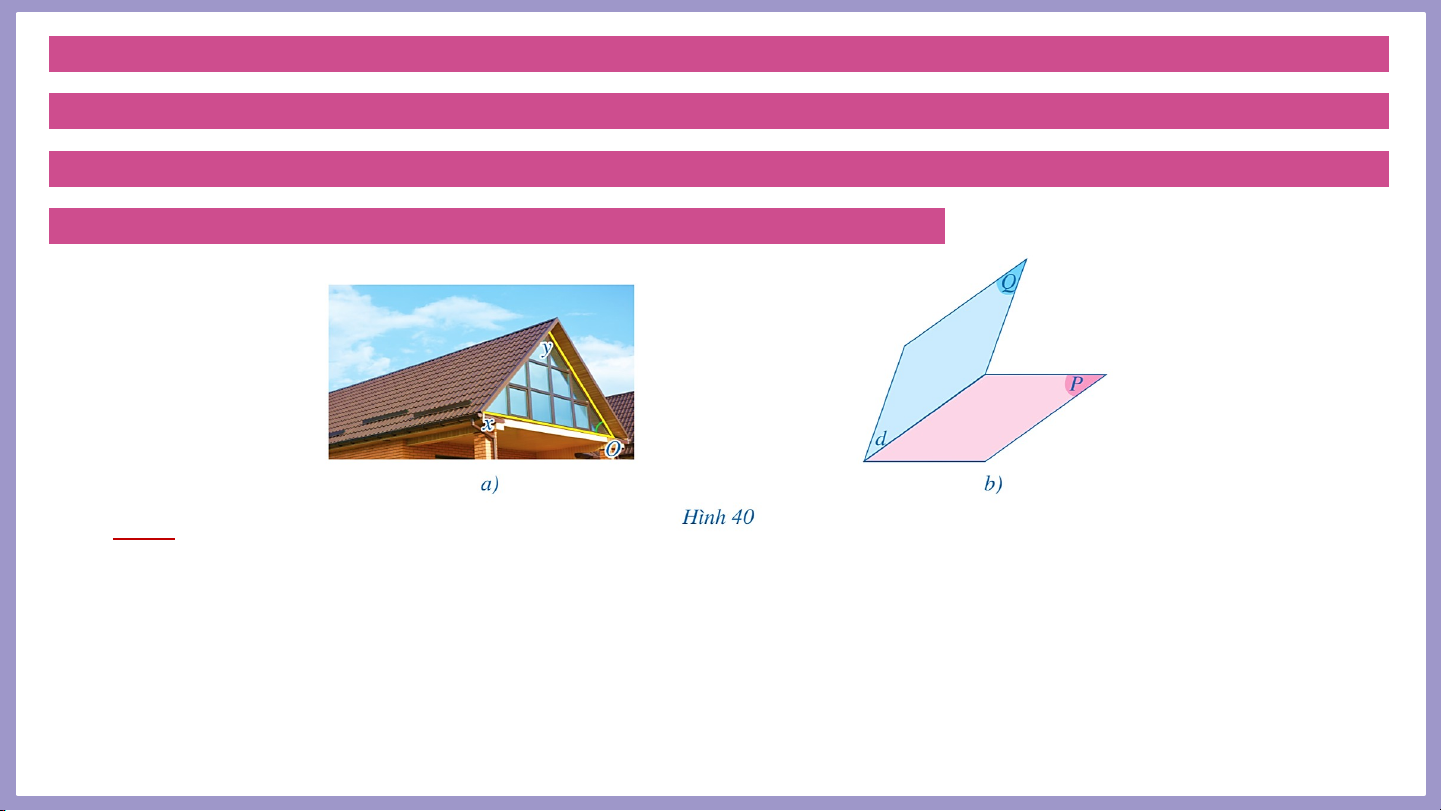
Hình 40 và cho biết góc nhị diện nào phản ánh độ dốc của mái. Giải
Giả sử nửa mặt phẳng (P) (minh hoạ mặt phẳng nằm ngang) và nửa mặt phẳng (Q) (minh
hoạ mái nhà) cắt nhau theo giao tuyến d (Hình 40b). Khi đó góc nhị diện có cạnh là đường
thẳng d, hai mặt lần lượt là (P) và (Q) phản ánh độ dốc của mái. Độ dốc đó cũng được
phản ánh bởi góc phẳng nhị diện xOy của góc nhị diện trên (Hình 40a).
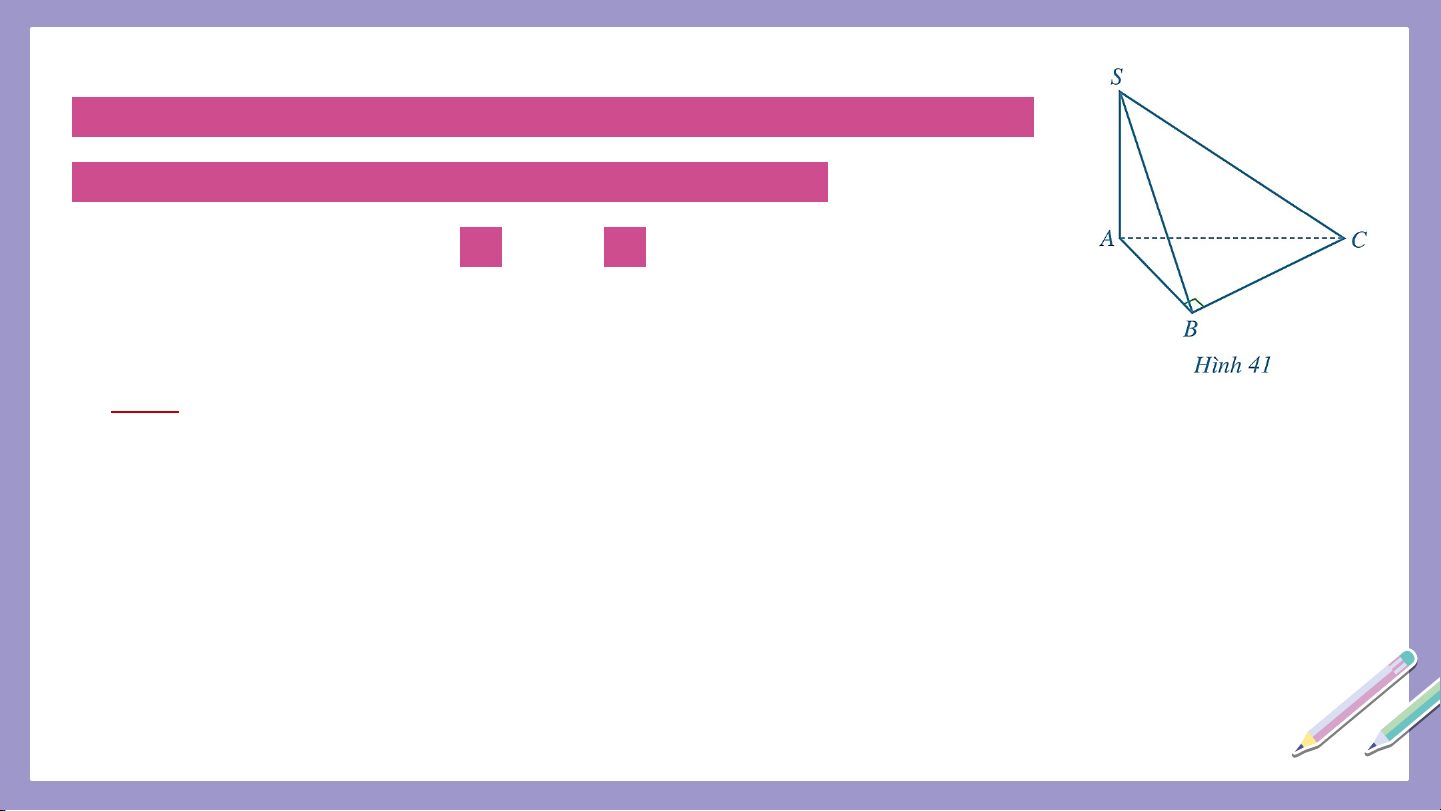
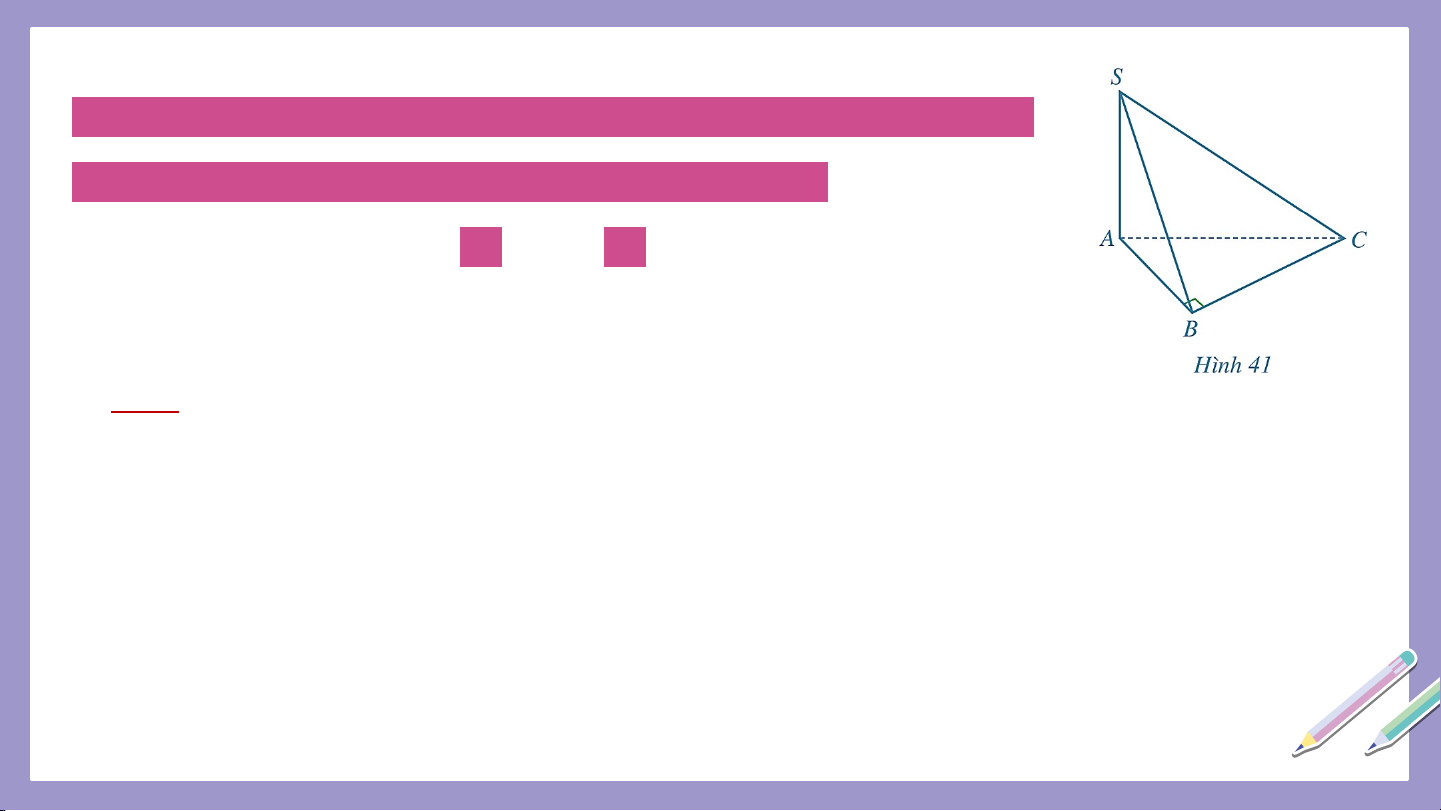
Ví dụ 5: Cho hình chóp có đáy là tam giác vuông cân tại ,
(Hình 41). Tính số đo của mỗi góc nhị diện sau: a) b) Giải a) Vì nên .
Do đó, góc là góc phẳng nhị diện của góc nhị diện
Do tam giác vuông cân tại nên
Vậy số đo của góc nhị diện bằng .
Ví dụ 5: Cho hình chóp có đáy là tam giác vuông cân tại ,
(Hình 41). Tính số đo của mỗi góc nhị diện sau: a) b) Giải
b) Vì nên . Mà nên suy ra .
Do đó góc là góc phẳng nhị diện của góc nhị diện
Trong tam giác vuông , ta có:
Suy ra Vậy số đo của góc nhị diện bằng . Luyện tập 3
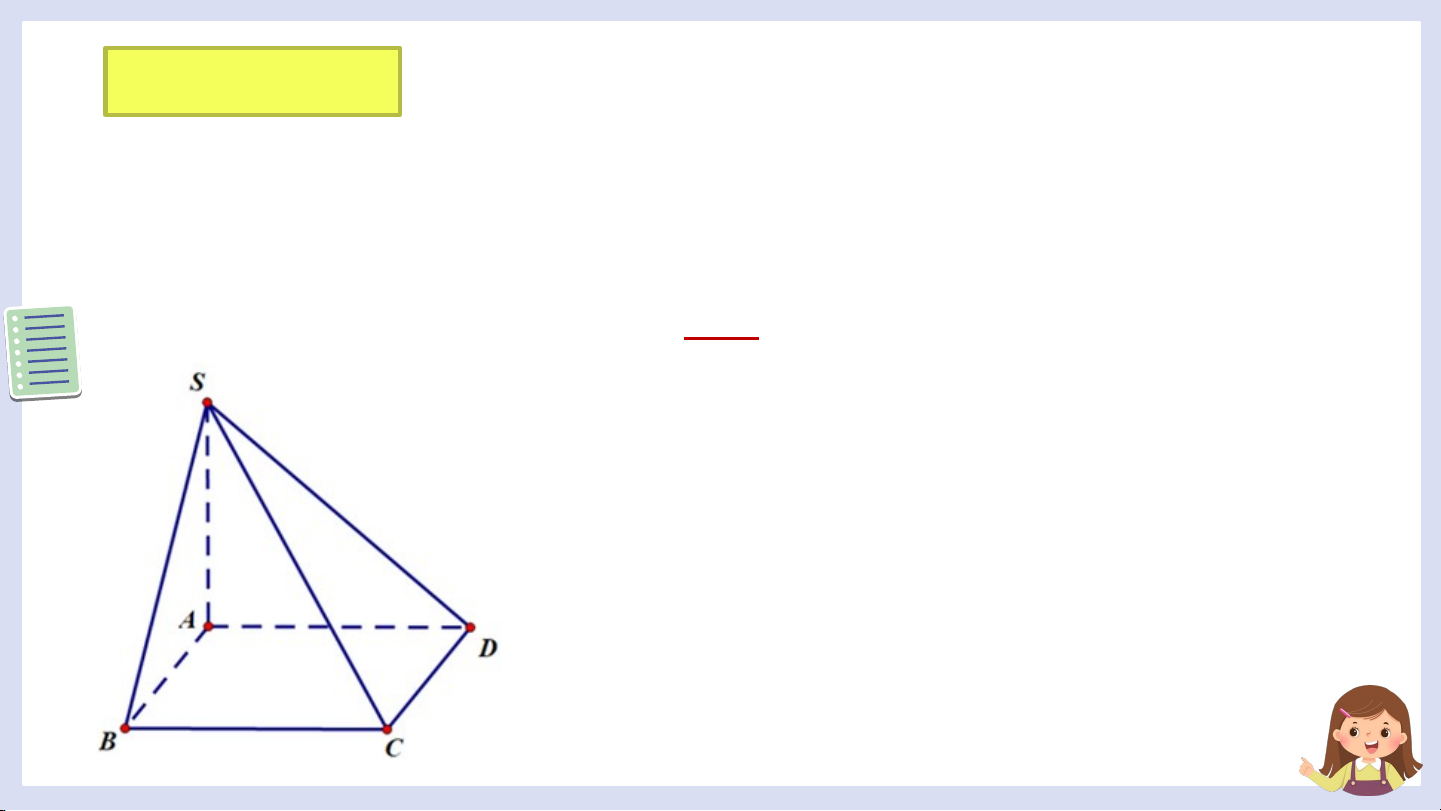
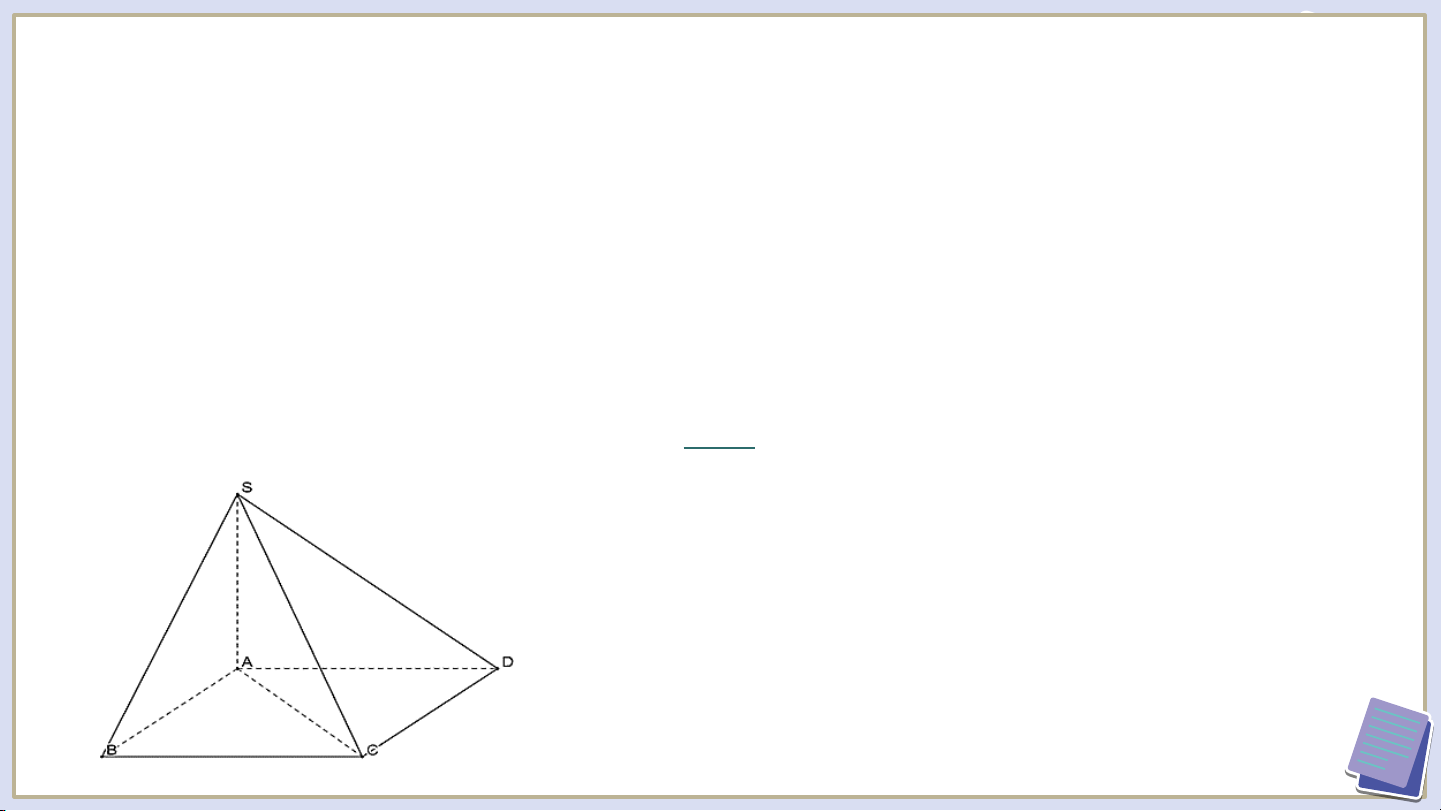
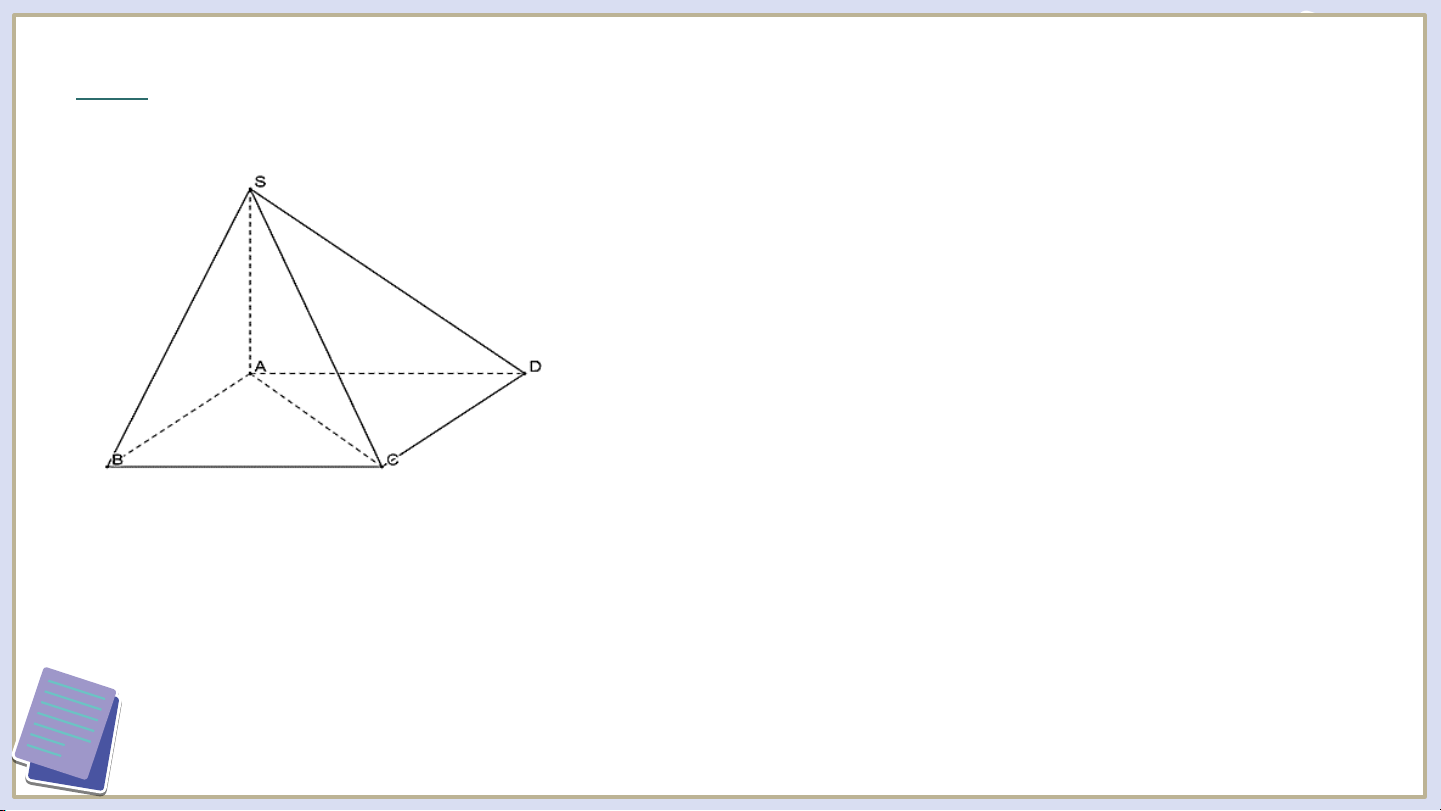
Cho hình chóp có đáy là hình vuông và .
Tính số đo của mỗi góc nhị diện sau: a); b) . Giải
a) Vì nên góc nhị diện là góc .
b) Vì nên góc nhị diện là góc . LUYỆN TẬP Trò Chơi “Đua xe”
Câu 1. Cho hình chóp có tam
giác đều cạnh . Góc giữa và A 30∘ C 45∘ B D 60∘ 90∘
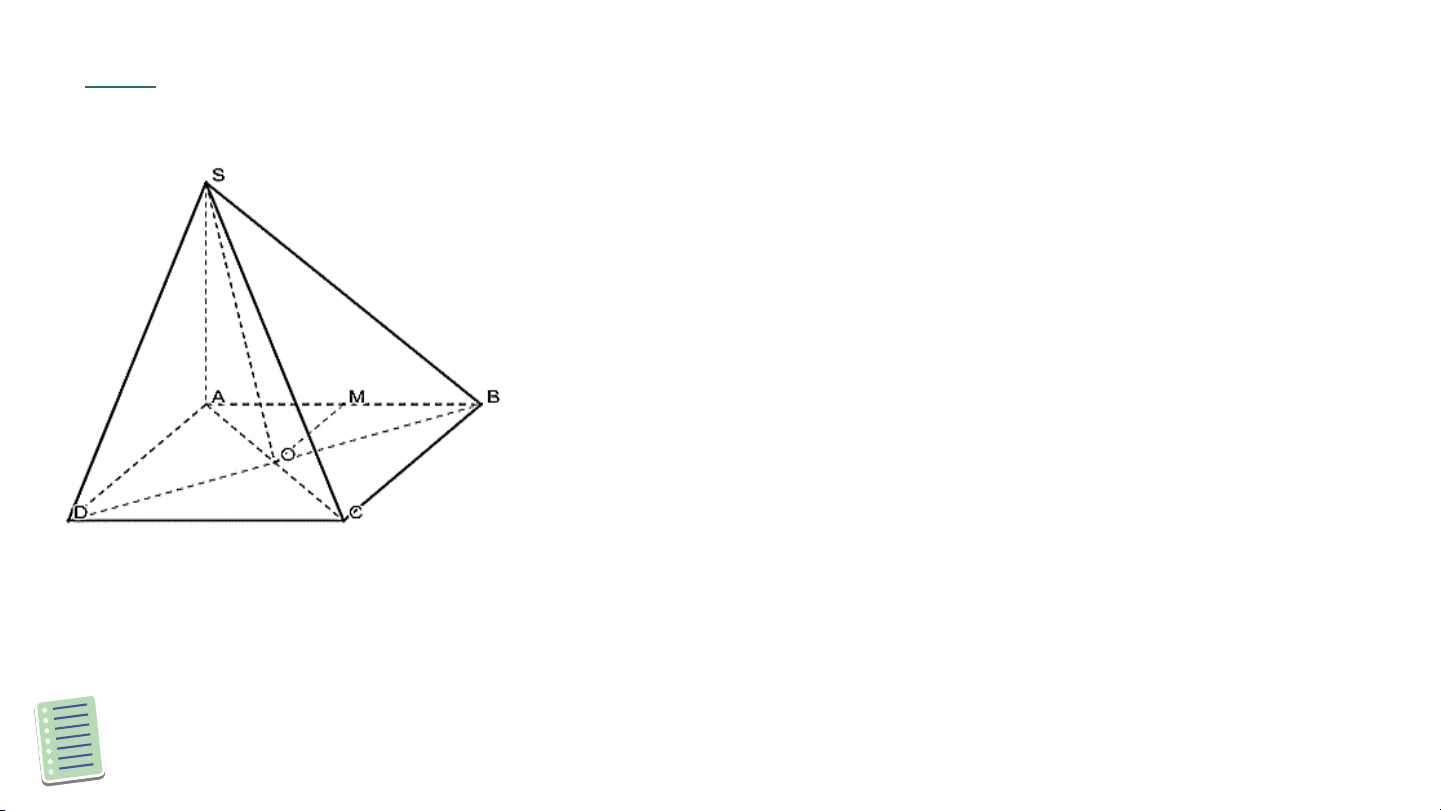
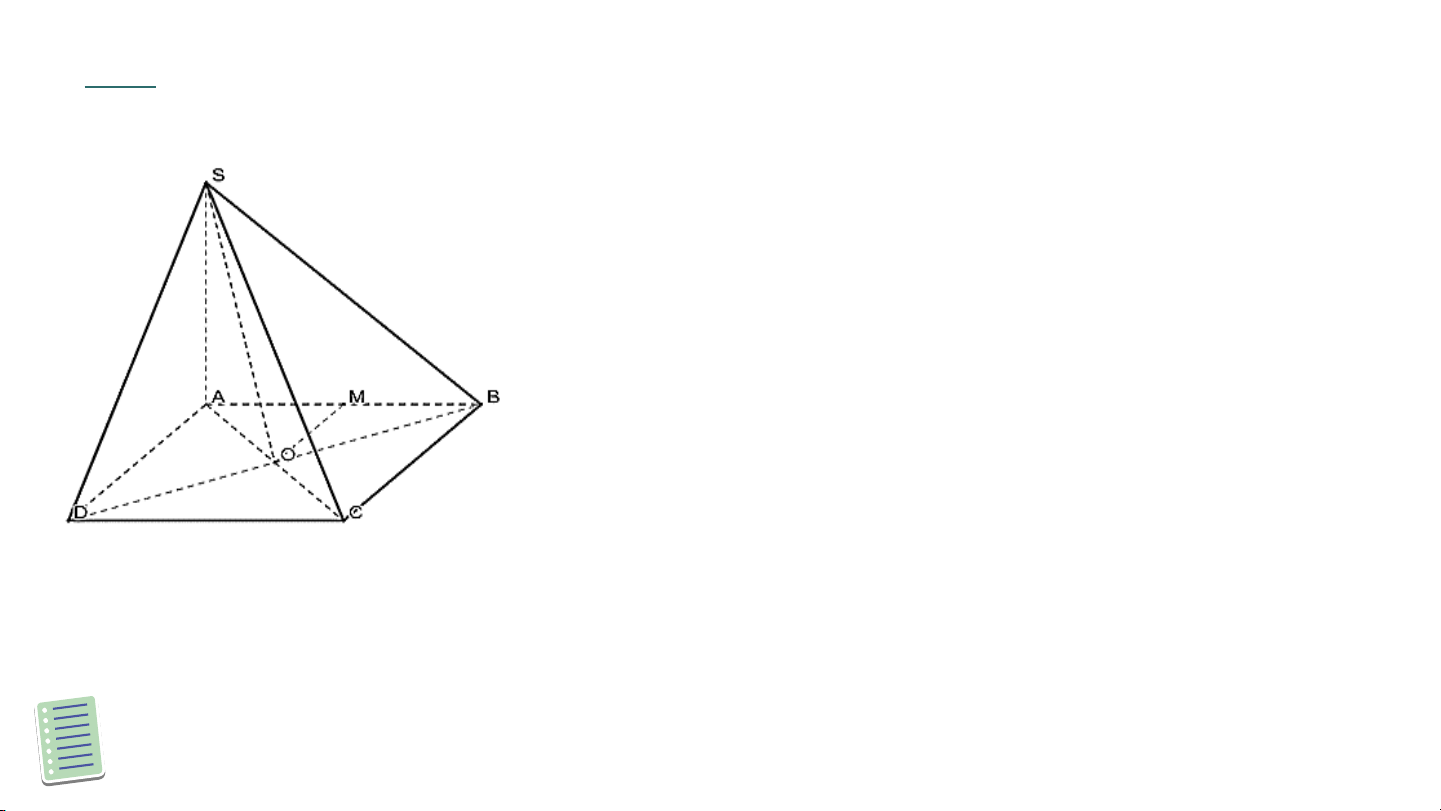
Câu 2. Cho hình chóp đáy là hình chữ nhật,
Gọi là giao điểm hai đường chéo và của
hình chữ nhật. Góc phẳng nhị diện là: A ^ 𝑆𝑂𝐴 C
^𝑆𝐻𝐴 (𝐻là chân đường cao hạ từ 𝑆xuống 𝐵𝐷) B ^ D 𝑆𝐵𝐴 ^ 𝑆𝐷𝐴
Câu 3. Cho hình lăng trụ có đáy là tam giác
đều. Hình chiếu vuông góc của đỉnh lên mặt
phẳng là trung điểm của cạnh . Góc phẳng nhị diện là A ^ 𝐴′𝐻𝐶 C ^ 𝐴′𝐵𝐶 B ^ D 𝐴′ 𝐴𝐶 ^ 𝐴′𝐵′𝐶
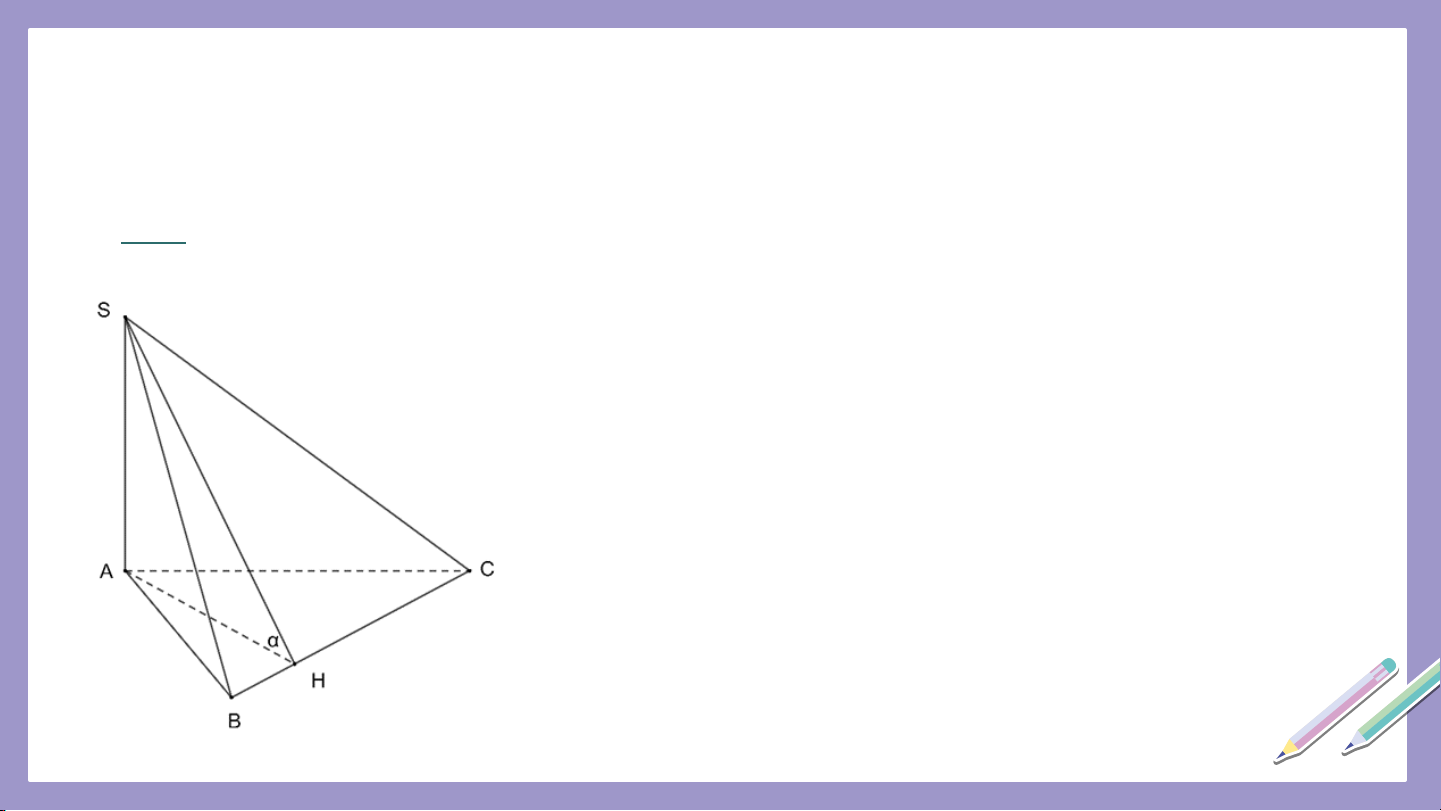
Câu 4. Cho hình chóp có đáy là tam giác
vuông với cạnh huyền . Hình chiếu vuông góc
của lên trùng với trung điểm . Biết . Góc giữa và A 30𝑜 C 60𝑜 B D 45𝑜 75𝑜
Câu 5. Cho hình chóp có đáy là hình vuông
cạnh , vuông góc với mặt phẳng đáy, . Góc
giữa đường thẳng và mặt phẳng A 30𝑜 C 60𝑜 B D 45𝑜 90𝑜
Bài 1 (SGK – tr.94) Cho hình chóp có đáy là hình thoi cạnh và
a) Tính số đo của góc nhị diện
b) Tính số đo của góc nhị diện
c) Biết , tính số đo của góc giữa đường thẳng và mặt phẳng . Giải a) Ta có
Ta có là tam giác đều cạnh , vậy Giải b) Ta có
là tam giác đều cạnh , nên ta có . Vậy
c) Do nên là hình chiếu của trên
Suy ra góc giữa đường thẳng và mặt phẳng bằng Ta có vuông cân tại nên
Bài 2 (SGK – tr.94) Cho hình chóp có đáy là hình vuông, hai đường
thẳng và cắt nhau tại , tam giác là tam giác đều.
a) Tính số đo của góc giữa đường thẳng và mặt phẳng
b) Chứng minh rằng Tính số đo của góc giữa đường thẳng và mặt phẳng
c) Gọi là trung điểm của cạnh . Tính số đo của góc nhị diện Giải
a) Góc giữa đường thẳng và bằng góc . Do đều, suy ra .
Vậy góc giữa đường thẳng và bằng . b) Do ; Suy ra .
Vậy góc giữa đường thẳng và mặt phẳng bằng . Giải c) Ta có vuông cân tại
là đường trung tuyến trong
suy ra là đường phân giác của Số đo góc nhị diện
Bài 6 (SGK – tr.94) Cho hình chóp có . Gọi là số đo của góc nhị diện Chứng minh rằng
tỉ số diện tích của hai tam giác và bằng . Giải Kẻ đường cao Ta có
Vậy so đo góc nhị diện bằng vuông tại nên ta có Mặt khác Vậy VẬN DỤNG
Bài 3 (SGK – tr.94) Dốc là đoạn đường thẳng nối hai khu vực hay
hai vùng có độ cao khác nhau. Độ dốc được xác định bằng góc giữa
dốc và mặt phẳng nằm ngang, ở đó độ dốc lớn nhất là 100%, tương
ứng với góc 90 (độ dốc 10% tương ứng với góc 9). Giả sử có hai
điểm A,B nằm ở độ cao lần lượt là 200 m, 220 m so với mực nước
biển và đoạn dốc AB dài 120 m. Độ dốc đó bằng bao nhiêu phần trăm
(làm tròn kết quả đến hàng phần trăm)? Giải
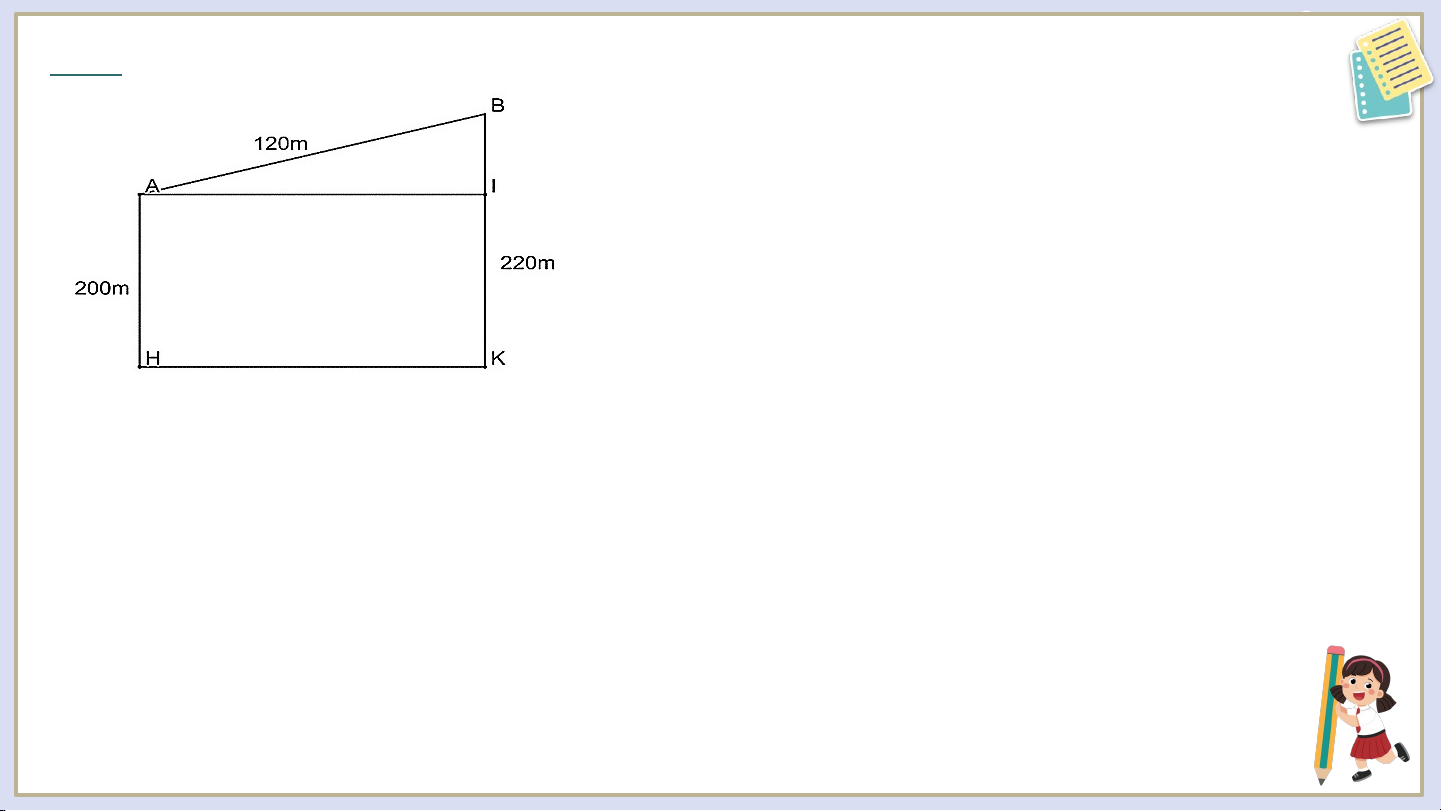
Mô hình hóa như hình vẽ, với là chiều dài con
dốc, là độ cao của điểm so với mặt nước
biển, là độ cao của điểm so với mặt nước
biển, là chiều cao của con dốc, độ lớn của góc chỉ độ dốc. Ta có .
là hình chữ nhật, suy ra Vì vuông tại nên ta có tương ứng với
Vậy độ dốc của con dốc đó là
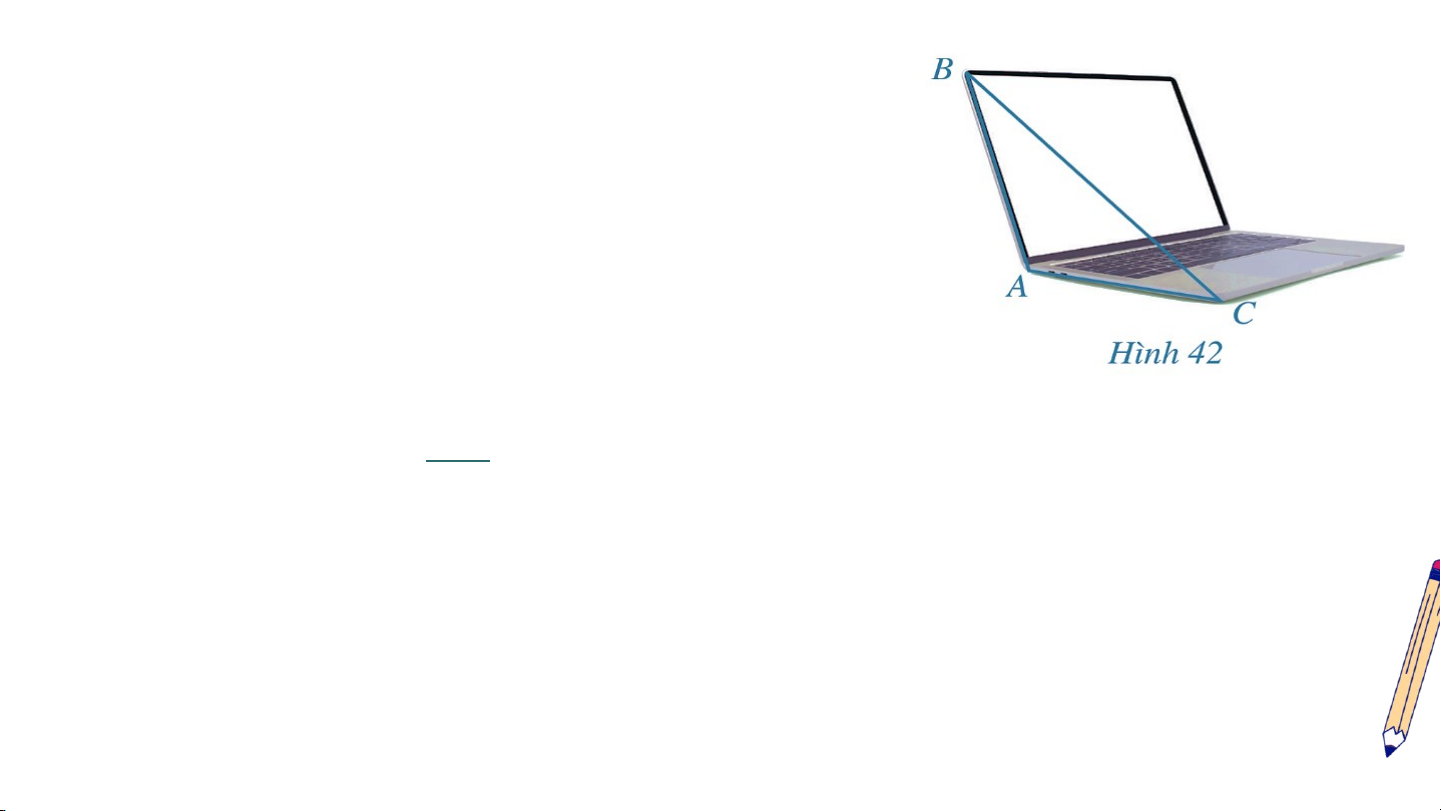
Bài 4 (SGK – tr.94) Trong Hình 42, máy tính xách tay
đang mở gợi nên hình ảnh của một góc nhị diện. Ta gọi
số đo góc nhị diện đó là độ mở của màn hình máy tính.
Tính độ mở của màn hình máy tính đó, biết tam giác có
độ dài các cạnh là và cm. Giải
Độ mở của màn hình máy tính bằng số đo góc
Áp dụng định lý cosin vào ta có
Vậy độ mở của máy tính bằng
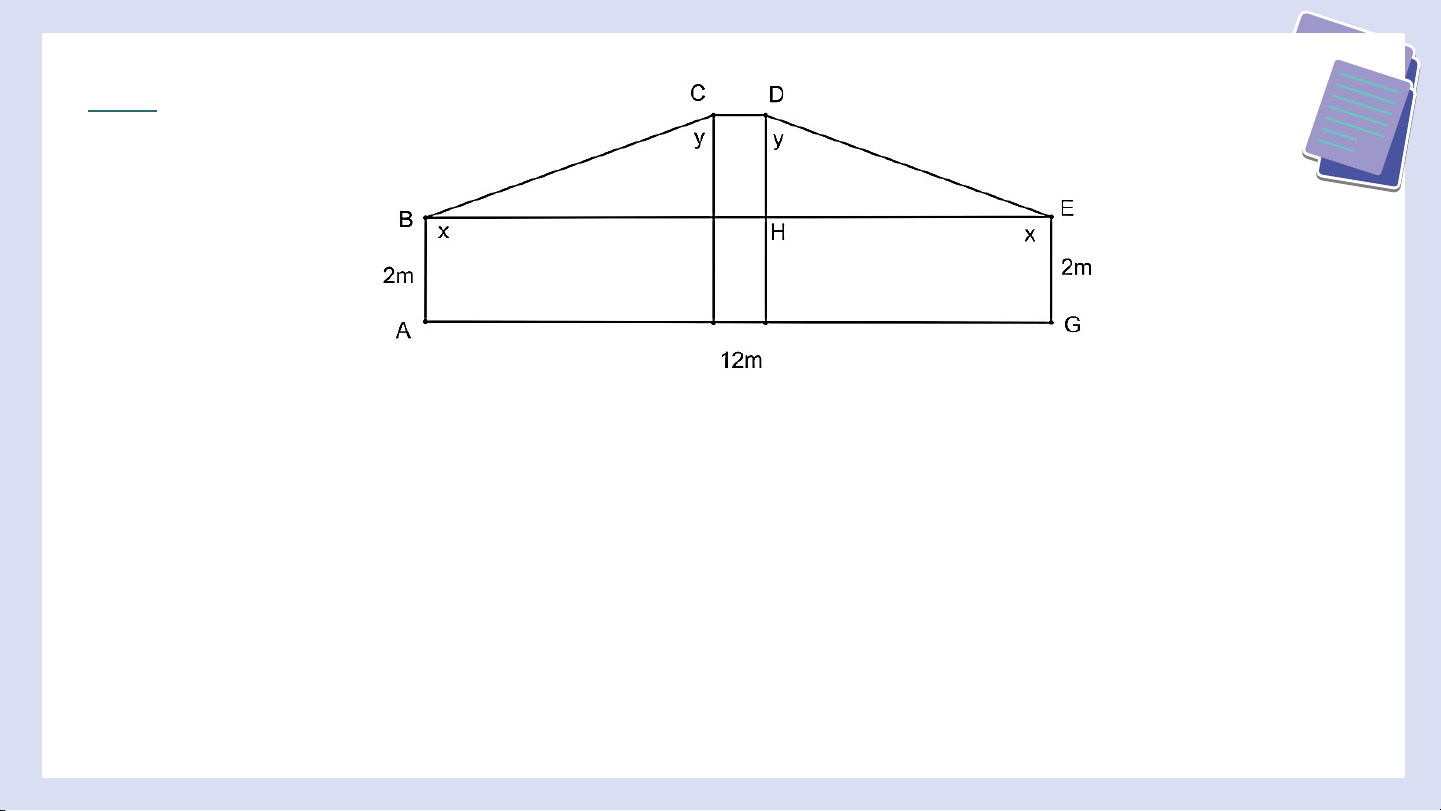
Bài 5 (SGK – tr.94) Trong Hình 43, xét các góc nhị diện có góc phẳng
nhị diện tương ứng là trong cùng mặt phẳng. Lục giác nằm trong mặt phẳng đó có ,
Biết rằng khoảng cách từ và đến
là , . Tìm (làm tròn kết quả đến
hàng đơn vị theo đơn vị độ). Giải Kẻ và cắt tại ;
Khi đó ta có vuông tại và Ta có Vậy ta có HƯỚNG D ẪN VỀ NHÀ
 Ôn tập kiến thức đã học.
 Hoàn thành bài tập trong SBT.
 Đọc và chuẩn bị trước Bài 4. Hai mặt phẳng vuông góc. CẢM ƠN CÁC EM ĐÃ THEO DÕI BÀI HỌC!
Document Outline

• Slide 1
• KHỞI ĐỘNG
• Slide 3
• NỘI DUNG BÀI HỌC
• I. GÓC GIỮA ĐƯỜNG THẲNG VÀ MẶT PHẲNG
• Slide 6
• Slide 7
• Slide 8
• Slide 9
• Slide 10
• Slide 11
• Slide 12
• Slide 13
• Slide 14
• II. GÓC NHỊ DIỆN
• 1. Khái niệm
• Slide 17
• Slide 18
• Slide 19
• Slide 20
• Slide 21
• 2. Số đo của góc nhị diện
• Slide 23
• Slide 24
• Slide 25
• Slide 26
• Slide 27
• Slide 28
• Slide 29
• LUYỆN TẬP
• Trò Chơi “Đua xe”
• Slide 32
• Slide 33
• Slide 34
• Slide 35
• Slide 36
• Slide 37
• Slide 38
• Slide 39
• Slide 40
• Slide 41
• Slide 42
• VẬN DỤNG
• Slide 44
• Slide 45
• Slide 46
• Slide 47
• Slide 48
• HƯỚNG DẪN VỀ NHÀ
• Slide 50