Giáo án điện tử Toán 6 Bài 12 Cánh diều: Ước chung và ước chung lớn nhất

Bài giảng PowerPoint Toán 6 Bài 12 Cánh diều: Ước chung và ước chung lớn nhất hay nhất, với thiết kế hiện đại, dễ dàng chỉnh sửa giúp Giáo viên có thêm tài liệu tham khảo để soạn Giáo án Toán 6. Mời bạn đọc đón xem!

11 6 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Bài giảng điện tử Toán 6

Môn: Toán 6

Sách: Cánh diều

Thông tin:

31 trang 3 tháng trước

Tác giả:

Profile Tin Hin



!
"
!
"
#
!
$
$
%
!
&
'
(
'
!
#
(
!
"
!
"
#
!
$
$
%
!
&
'
(
'
!
#
(
•
)*+,
&
"
%
" &
& # % '
 % # #'
--&-%
./0
Số tự nhiên n được gọi là ước chung của
hai số a và b nếu n vừa là ước của a vừa
là ước của b.
Số lớn nhất trong các ước chung của a và
b được gọi là ước chung lớn nhất của a và
b.
12
3/4

5673809:9;<55
=>5?=@-<55=
>5?=@
A>& ?#'@!B--&-%C
>& ?#'@!%
2809
•
5@DE'<5#"%F'G5
<5#G5<5"%
•
=@DE'6H9I3<5#
#'F'<5#'6H9I3
<5#
JKL
M DE N 3O  +: P3  
<5=5QE5?=?/
<5=5QE5?=?
2809
•
DE$<5#?#(?%&F$G5
<5#?G5<5#(?G5
<5%&
!
"
!
"
#
!
$
$
%
!
&
'
(
'
!
#
(
!
"
!
"
#
!
$
$
%
!
&
'
(
'
!
#
(
•
)*+,
5@>#?&%@!B??&?#?%?C
=@>#?&%@!
@! !% &!#
#!& %! !
./0
<553QE<5
<5K
2809&
•
F<55=+R
>5?=@!' OI;QES53
TQE<55= ?%?
 ?# ?' 
FU=V;9W7
;QEX5G5QE2OE
!
"
!
"
#
!
$
$
%
!
&
'
(
'
!
#
(
!
"
!
"
#
!
$
$
%
!
&
'
(
'
!
#
(
•
)*+,&
./0
Tìm ước chung lớn nhất bằng cách phân tích
các số ra thừa số nguyên tố:
Bước 1: Phân tích mỗi số ra thừa số nguyên tố.
Bước 2: Chọn ra các thừa số nguyên tố chung.
Bước 3: Với mỗi thừa số nguyên tố chung, ta
chọn lũy thừa với số mũ nhỏ nhất.
Bước 4: Lấy tích của các lũy thừa đã chọn, ta
nhận được ước chung lớn nhất cần tìm.
2809#
•
%!$&
•
%!
&
&
&
•
!Y>%-%@!&
!'
JKL
M/53QE+Z)6HSG5
QE 2O E  F  <5
K=V
M/535/)=F
>5?=@!=
[*
>#'?%@!%
53QE2OE\5
!
"
!
"
#
!
$
$
%
!
&
'
(
'
!
#
(
!
"
!
"
#
!
$
$
%
!
&
'
(
'
!
#
(
•
)*+,#
•
>'?$@!
•
./0
53QE2OE\553QES
=V
2809"
•
S>#?&"@!
!Y53QE#&"53QE2OE
\5
./0
]WQEE33I9WQES^U_53QE
2OE\5
!
"
!
"
#
!
$
$
%
!
&
'
(
'
!
#
(
!
"
!
"
#
!
$
$
%
!
&
'
(
'
!
#
(
•
)*+,"
•
5@S>#?(@!
!Y53QE#(53QE2OE\5
•
=@S`XKP9WQE
a309
•
DE<553QEN3O=6F
ab3FI;QEN3O+RSQE
QE
a309
•
5@>## ?#("@!B?"??""C
•
=@>## ?#("@!""
a309#
•
126 = 2.3
2
.7
•
150 = 2.3.5
2
•
=> ƯCLN(126, 150) = 2.3 = 6
•
  ƯC(126, 150) = {1, 2, 3, 6}
a309"
a309$
cP3DE+,3+:353R5>+,3@>5J@
5S#5?& 5?5
!Y5!>#?& @
#!
&
&& !&"!Y>#?& @!&!%
F5!>#?& @!Y5!%
02S`35;=*3R%+,3
d_P09b
M3;63/e<5=3
MU=309&?%?'X)D.
+PUfFUg3?UbX,
MhPX=3U3ia3&a,3
=,3jk)
3/PQ5
| 1/31
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

§ 12: ƯỚC CHUNG VÀ ƯỚC CHUNG LỚN NHẤT 12 02 : 2 I. Ước ch =
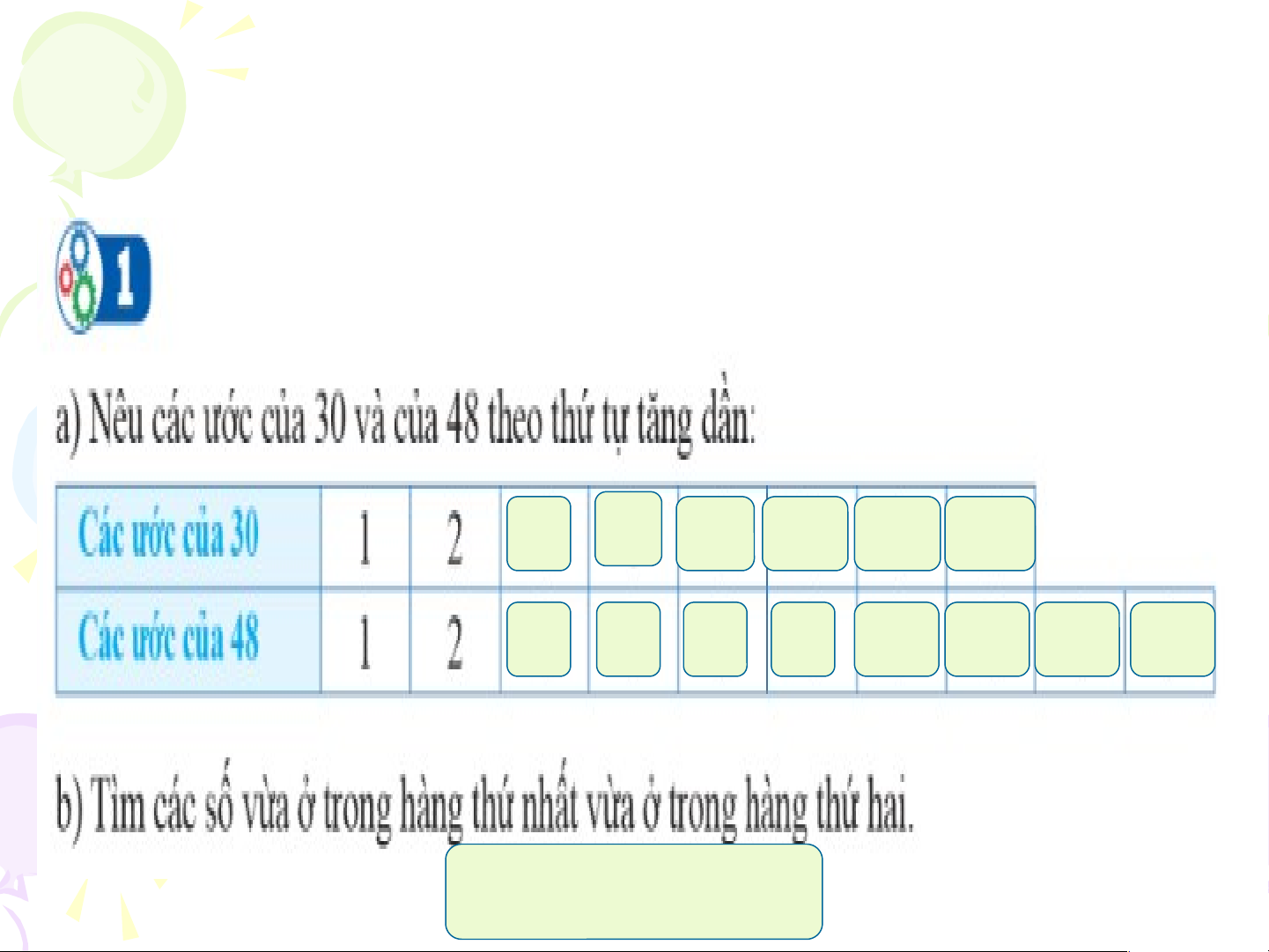
ung và ước chung lớn nhất 511• Hoạt động 1: 57 46 12 :02 2: = 2 23 = 78 51 9 1 8 57 3 5 6 10 15 30 :46 2: 3 4 6 8 12 16 24 48 = 2 4= 9 23 78 9 8 1; 2; 3 ; 6 : 2 = 4 9 Kết luận:
Số tự nhiên n được gọi là ước chung của
hai số a và b nếu n vừa là ước của a vừa là ước của b.
Số lớn nhất trong các ước chung của a và
b được gọi là ước chung lớn nhất của a và b. Quy ước:
Viết tắt ước chung là ƯC và ước chung lớn nhất là ƯCLN
Ta kí hiệu: Tập hợp các ước chung của a và
b là ƯC(a, b); ước chung lớn nhất của a và b là ƯCLN (a, b).
VD: ƯC ( 30, 48) = {1; 2; 3; 6}. ƯCLN (30, 48) = 6 Luyện tập 1:
• a) Số 8 là ước chung của 24 và 56 vì 8 vừa
là ước của 24 vừa là ước của 56.
• b) Số 8 không phải là ước chung của 14 và
48 vì 8 là ước của 48 nhưng không phải là ước của 14. * Chú ý:
- Số tự nhiên n được gọi là ước
chung của ba số a, b, c nếu n là ước của ba số a, b, c. Luyện tập 2:
• Số 7 là ước chung của 14, 49, 63 vì 7 vừa
là ước của 14, vừa là ước của 49, vừa là ước của 63. 12 02 : 2 = • Hoạt động 2: 511 57 46 Kết luận: 12:02
Ước chung của hai số là ước của ước 2: chung lớn nhất của chúng. = 2 23 = 78 51 9 1
a)ƯC(2 84, 36) = {1, 2, 3, 4, 6, 12} 57 :46 b) ƯCLN(24, 36) = 12. 2: = 2 c)12 : 1 = 12 12 : 2 = 6 12 : 3 = 4 4= 9 12 : 4 =23 3 12 : 6 = 2 12 : 12 = 1 78 9 8 : 2 = 4 9 Luyện tập 3:
• Vì ước chung của a và b đều là
ƯCLN(a, b) = 80 nên tất cả các số có hai
chữ số là ước chung của a và b là: 10, 16, 20, 40, 80. 12 02 : 2
II. Tìm ước= chung lớn nhất bằng cách phân tích 51 các số ra thừ 1 a số nguyên tố. 57 46• Hoạt động 3: 12 :02 2: = 2 23 = 78 51 9 1 8 57 :46 2: = 2 4= 9 23 78 9 8 : 2 = 4 9 Kết luận:
Tìm ước chung lớn nhất bằng cách phân tích
các số ra thừa số nguyên tố:
Bước 1: Phân tích mỗi số ra thừa số nguyên tố.
Bước 2: Chọn ra các thừa số nguyên tố chung.
Bước 3: Với mỗi thừa số nguyên tố chung, ta
chọn lũy thừa với số mũ nhỏ nhất.
Bước 4: Lấy tích của các lũy thừa đã chọn, ta
nhận được ước chung lớn nhất cần tìm. Luyện tập 4: • 126 = 2.7.32 • 162 = 23. 33
• => ƯCLN (126; 162) = 2.32 = 18 * Chú ý:
- Nếu hai số đã cho không có thừa
số nguyên tố chung thì ƯCLN của chúng bằng 1
- Nếu a chia hết cho b thì ƯCLN (a,b) = b. Chẳng hạn: ƯCLN (48, 16) = 16 12 02 : 2 III. Hai số n = guyên tố cùng nhau 511 57 46• Hoạt động 4: 12 :02 2: = 2 23 = 78 51 9 1 • ƯCLN ( 8, 27) = 1 8 57 :46 • 2: Kết luận: =2
Hai số nguyên tố cùng nhau là hai số có ước chung 4= 9 lớn nhất bằng 1. 23 78 9 8 : 2 = 4 9 Luyện tập 5: • Có: ƯCLN (24,35) = 1
=> Hai số 24 và 35 là hai số nguyên tố cùng nhau. 12 02 : 2 = • Hoạt động 5: 511 57 46 12 :02 2: = 2 • a) Có 23 = : ƯCLN(4,9) = 1. 78 51 => Hai số 9 1
4 và 9 là hai số nguyên tố cùng nhau. 8 57 • b) Có th :4 ể6 rút gọn phân số: 2: Kết luận: =2 Phân số tối g 4= 9
iản là phân số có tử và mẫu là hai số 23 nguyên tố c78ùng nhau. 9 8 : 2 = 4 9 Bài Tập 1
• Số 1 là ước chung của hai số tự nhiên bất kì.
Bởi vì tất cả các số tự nhiên đều có ước số là số 1. Bài Tập 2
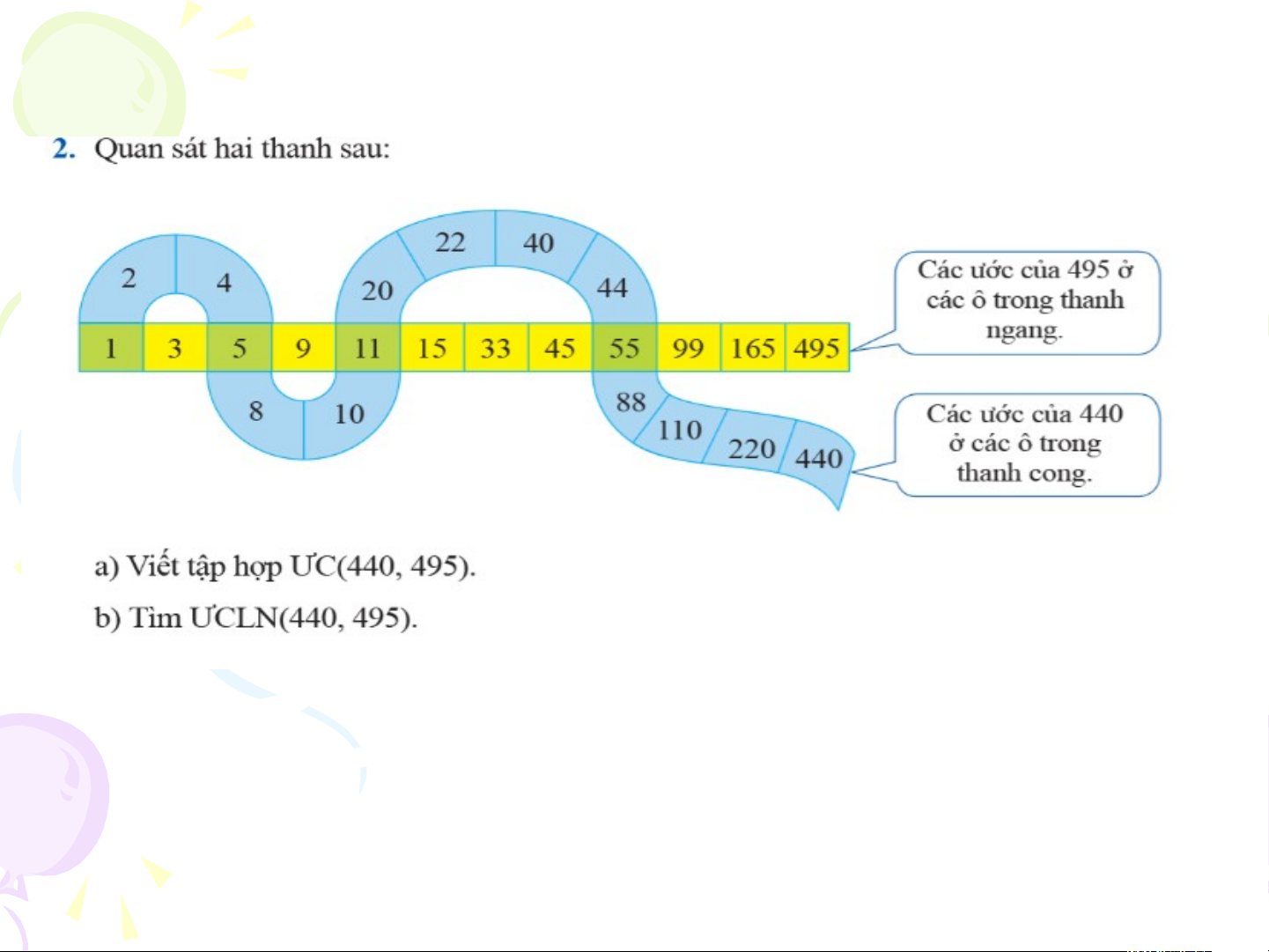
• a) ƯC(440,495) = {1, 5, 11, 55} • b) ƯCLN(440, 495) = 55 Bài Tập 4 • 126 = 2.32.7 • 150 = 2.3.52
• => ƯCLN(126, 150) = 2.3 = 6
• ƯC(126, 150) = {1, 2, 3, 6} Bài Tập 5 Bài Tập 7
Gọi: Số đội được chia nhiều nhất là: a(đội)(a N*)
Ta có 24 a, 30 a, a lớn nhất =>a= ƯCLN (24,30)
24=23.3 30= 2.3 .5 => ƯCLN (24,30) = 2. 3=6
Vì a= ƯCLN (24,30) => a = 6
Vậy có thể chia các bạn thành nhiều nhất 6 đội.
Hướng dẫn học tập ở nhà.
- Ghi nhớ các kiến thức của bài
-Làm bài tập 3,6,8 trong SGK và
đọc mục tìm tòi, mở rộng
-Đọc trước bài mới “Bài 13:Bội
chung và bội chung nhỏ nhất” cho tiết học sau.
Document Outline

  • Slide 1
  • Slide 2
  • § 12: ƯỚC CHUNG VÀ ƯỚC CHUNG LỚN NHẤT
  • Slide 4
  • Slide 5
  • Slide 6
  • Slide 7
  • Luyện tập 1:
  • Slide 9
  • Luyện tập 2:
  • Slide 11
  • Slide 12
  • Slide 13
  • Luyện tập 3:
  • Slide 15
  • Slide 16
  • Slide 17
  • Luyện tập 4:
  • Slide 19
  • Slide 20
  • Slide 21
  • Luyện tập 5:
  • Slide 23
  • Slide 24
  • Bài Tập 1
  • Bài Tập 2
  • Bài Tập 4
  • Bài Tập 5
  • Bài Tập 7
  • Slide 30
  • Slide 31