

















Preview text:
Thử thách nhỏ:
Lịch xuất bến của một số xe buýt tại bến xe Mỹ Đình (Hà Nội)
được ghi ở bảng dưới đây. Giả sử các xe buýt xuất bến cùng
lúc vào 10 giờ 35 phút. Hỏi vào các thời điểm nào trong ngày
(từ 10 giờ 35 phút đến 22 giờ) các xe buýt này lại xuất bến cùng một lúc? Bến xe Mỹ Đình Số xe Thời gian Xe 16 15 phút/chuyến Xe 34 9 phút/chuyến Xe 30 10 phút/chuyến Giải:
3. Quy đồng mẫu các phân số
*) Vận dụng BCNN để tìm mẫu chung của hai phân số a c
Để quy đồng mẫu hai phân số và , ta phải tìm mẫu b chung củ
d a hai phân số đó.
Thông thường ta nên chọn mẫu chung là bội chung nhỏ nhất của hai mẫu. 7
Ví dụ: Quy đồng mẫu hai phân số 5 và 8 12
Ta có BCNN(8, 12) = 24 nên 5 5.3 15 8 8.3 24 7 7.2 14 12 12.2 24 7 4 ?
Quy đồng mẫu hai phân số và 9 15 Giải: Ta có 9 = 32 15 = 3 . 5
BCNN(9, 15) = 32 . 5 = 45 Do đó 7 7.5 35 9 9.5 45 4 4.3 12 15 15.3 45 Ví dụ 5: 3 5 1
Quy đồng mẫu các phân số sau: ; và 8 9 6 Giải:
Có thể chọn một bội chung
Ta có 8 = 23; 9 = 32; 6 = 2 . 3
khác 0 bất kì của các mẫu
làm mẫu chung. Tuy nhiên,
BCNN(8, 9, 6) = 23 . 32 = 72
người ta thường lấy BCNN 3 3.9 27 làm mẫu chung Do đó 8 8.9 72 5 5.8 40 9 9.8 72 1 1.12 12 6 6.12 72 Ví dụ 6:
Thực hiện phép tính: 1 1 a) 11 3 b) 4 6 12 8 Giải:
a) Ta có BCNN(4, 6) = 12 b) Ta có BCNN(12, 8) = 24 nên 1 1 nên 11 3 4 6 12 8 1.3 1.2 11.2 3.3 4.3 6.2 12.2 8.3 3 2 5 22 9 13 12 12 12 24 24 24 Luyện tập 3:
1 Quy đồng mẫu các phân số sau: 2 4 7 a)
5 và 7 b) ; và 12 15 Giải: 7 9 12
a) Ta có 12 = 22 . 3; 15 = 3 . 5 b) Ta có 7 = 7; 9 = 32; 12 = 22 . 3
BCNN(12, 15) = 22 . 3 . 5= 60
BCNN(7, 9, 12) = 22 . 32 . 7 = 252 5 5.5 25 2 2.36 72 Do đó Do đó 12 12.5 60 7 7.36 252 7 7.4 26 4 4.28 112 15 15.4 60 9 9.28 252 7 7.21 147 12 12.21 252
2 Thực hiện phép tính: 3 5 a) 7 5 b) 8 24 16 12 Giải:
a) Ta có BCNN(4, 6) = 12 b) Ta có BCNN(12, 8) = 24 7 5 nên 3 5 nên 8 24 16 12 3.3 5 7.3 5.4 8.3 24 16.3 12.4 14 21 20 24 48 48 7 1 12 48 LUYỆN TẬP
Bài 2.36: (SGK/53)
Tìm bội chung nhỏ hơn 200 của:
a)5 và 7 b) 3, 4 và 10 Giải: a) Ta có 5 = 5; 7 = 7 BCNN(5, 7) = 5 . 7 = 35
Suy ra BC(8, 6) = {0; 35; 70; 105; 140; 175; 210…}
Nên các bội chung nhỏ hơn 200 của 5 và 7 là
0 ; 35; 70; 105; 140; 175. Chú ý:
Nếu các hai đã cho nguyên tố cùng nhau thì BCNN
của chúng là tích của các số đó. Ví dụ: BCNN(5, 7) = 5 . 7 = 35
b) Ta có 3 = 3; 4 = 22; 10 = 2 . 5
Suy ra BC(3, 4, 10) = BCNN(3, 4, 10) = 22 . 3 . 5 = 60 {0; 60; 120; 240…}
Nên các bội chung nhỏ hơn 200 của 3, 4 và 10 là 0; 60; 120.
Bài 2.37: (SGK/53) Tìm BCNN của:
a)2 . 32 và 3 . 5 b) 2 . 5. 72 và 3 . 52 . 7 Giải:
a) BCNN(2 . 32, 3 . 5) = 2 . 32. 5 = 90
b) BCNN(2 . 5. 72, 3 . 52 . 7 ) = 2 . 3 . 52. 72 = 7350
Bài 2.38: (SGK/53)
Tìm BCNN của các số sau:
a)30 và 45 b) 18, 27 và 45 Giải:
a) Ta có 30 = 2. 3 . 5; 45 = 32. 5
BCNN(30, 45) = 2 . 32. 5 = 90
b) Ta có 18 = 2 . 32; 27 = 33 ; 45 = 32. 5
BCNN(18, 27, 45 ) = 2 . 33. 5 = 270
Bài 2.39: (SGK/53)
Tìm số tự nhiên a nhỏ nhất khác 0, biết rằng a 2 8 và a 32. Giải: Ta có a 2 8; a 3
2 và a nhỏ nhất khác 0 Nên a = BCNN(28, 32) 28 = 22. 7; 32 = 25
Suy ra BCNN(28, 32) = 25. 7 = 224. Vậy a = 224
Bài 2.40: (SGK/53)
Học sinh lớp 6A khi xếp thành 3 hàng, 4 hàng hay 9 hàng
đều vừa đủ. Biết số học sinh của lớp từ 30 đến 40.
Tính số học sinh của lớp 6A. Giải:
Gọi số học sinh của lớp 6A là x (x N và 3 0 x ) 40
Vì số học sinh khi xếp thành 3 hàng, 4 hàng hay 9 hàng đều vừa đủ Nên x 3 ; x 4 ; x 9 Suy ra x BC(3, 4, 9)
Ta có BCNN(3, 4, 9) = 22. 32 = 36
BC(3, 4, 9) = {0; 36; 72; …} Suy ra x {0; 36; 72; …} Mà 3 0 x 4 0 nên x = 36
Vậy lớp 6A có 36 học sinh.
Bài 2.41: (SGK/53)
Hai đội công nhân trồng được một số cây như nhau.
Mỗi công nhân đội I đã trồng 8 cây, mỗi công nhân đội hai
đã trồng 11 cây. Tính số cây mỗi đội đã trồng, biết rằng
số cây đó trong khoảng từ 100 đến 200 cây. Giải:
Gọi số cây mỗi đội đã trồng là x (x
N và 100 < x < 200)
Vì mỗi công nhân đội I trồng được 8 cây, mỗi công nhân đội hai đã
trồng 11 cây và hai đội trồng được một số cây như nhau. Nên x 8 ; x 1 1 Suy ra x BC(8, 11)
Ta có BCNN(8, 11) = 8 . 11 = 88
BC(8, 11) = {0; 88; 176; 352;…} Suy ra x
{0; 88; 176; 352; …}
Mà 100 < x < 200 nên x = 176. Vậy mỗi đội đã trồng được 176 cây.
Bài 2.42: (SGK/53)
Cứ 2 ngày, Hà đi dạo cùng bạn cún yêu quý của mình.
Cứ 7 ngày, Hà lại tắm cho cún. Hôm nay, cún vừa được đi
dạo, vừa được tắm. Hỏi sau ít nhất bao nhiêu ngày nữa thì cún
vừa được đi dạo, vừa được tắm? Giải:
Gọi số ngày ít nhất mà cún vừa được đi dạo, vừa được tắm là x (x N)
Vì cứ 2 ngày Hà đi dạo cùng bạn cún và cứ 7 ngày Hà lại tắm cho cún Nên x 2 và x 7 Suy ra x = BCNN(2, 7)
Ta có BCNN(2, 7) = 2 . 7 = 14 Suy ra x = 14
Vậy sau 14 ngày nữa thì cún vừa được đi dạo, vừa được tắm .
Bài 2.43: (SGK/53)
Quy đồng mẫu các phân số sau: 9 7 3 9 a) và 7 b) ; và 12 15 10 4 14 Giải:
a) Ta có 12 = 22 . 3; 15 = 3 . 5
b) Ta có 10 = 2 . 5; 4 = 22; 14 = 2 . 7
BCNN(12, 15) = 22 . 3 . 5= 60
BCNN(10, 4, 14) = 22 . 5 . 7 = 140 9 9.5 45 7 7.14 98 Do đó Do đó 12 12.5 60 10 10.14 140 3 3.35 105 7 7.4 26 4 4.35 140 15 15.4 60 9 9.10 90 14 14.10 140
Bài 2.44: (SGK/53)
Thực hiện phép tính: 7 2 a) 7 5 b) 11 7 20 15 Giải:
a) Ta có BCNN(7, 11) = 77
b) Ta có BCNN(12, 8) = 24 7 2 nên 7 5 nên 11 7 20 15 7.7 5.11 7.3 2.4 11.7 7.11 20.3 15.4 104 21 8 77 60 60 13 60
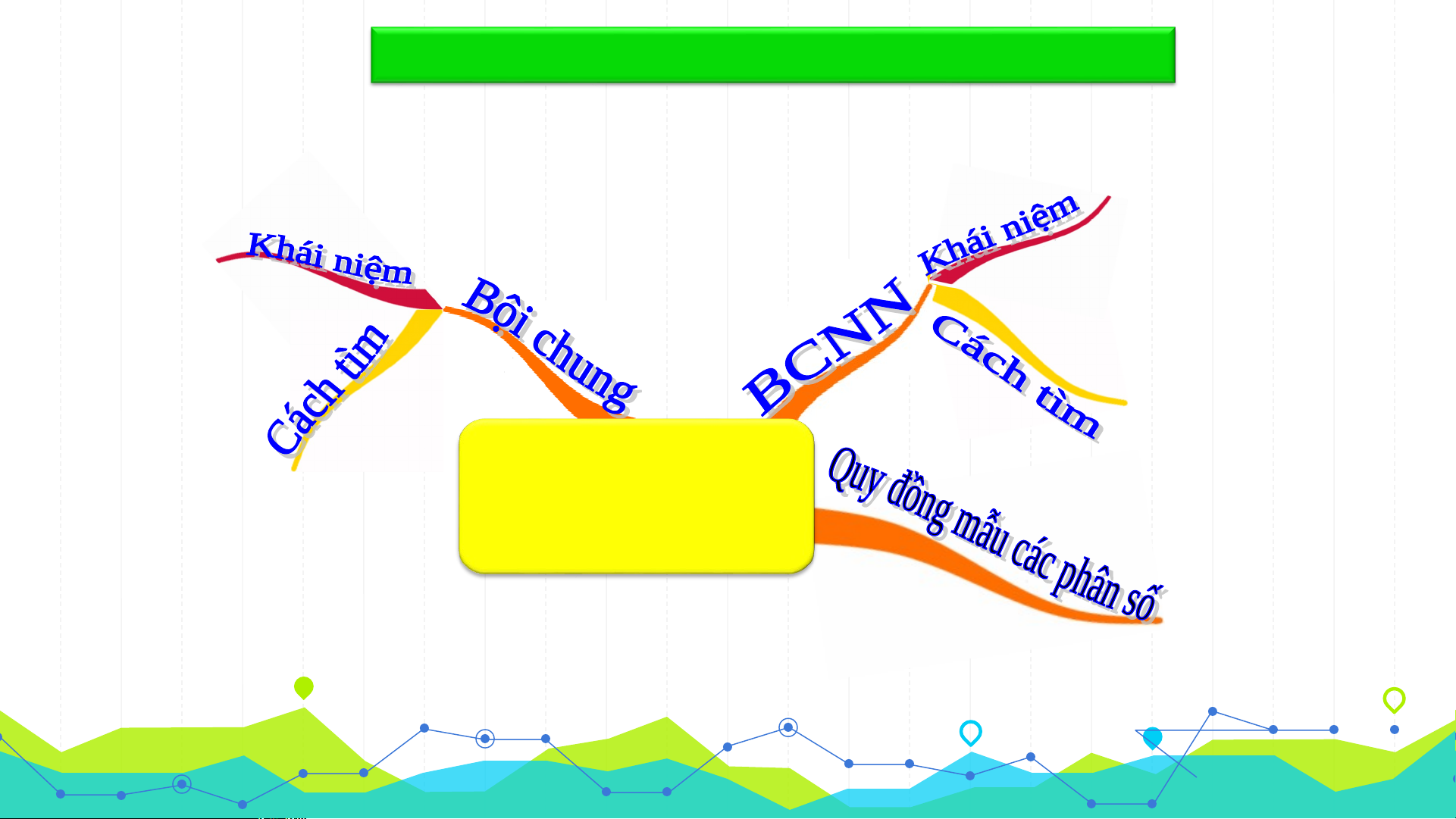
SƠ ĐỒ TƯ DUY TÓM TẮT NỘI DUNG BÀI HỌC BỘI CHUNG VÀ BỘI CHUNG NHỎ NHẤT
* Đối với bài học ở tiết học này:
Nắm được thế nào là bội chung,
bội chung nhỏ nhất.
Nắm vững cách tìm bội chung
và BCNN của hai hay nhiều số. BTVN: SGK.
Chuẩn bị bài cho tiết sau luyện tập
Document Outline
- PowerPoint Presentation
- Slide 2
- 3. Quy đồng mẫu các phân số
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25




