








Preview text:
GV: TRƯƠNG ĐÌNH NY HÌNH HỌC TRỰC QUAN
CHƯƠNG IV: MỘT SỐ HÌNH PHẲNG TRONG KHÔNG GIAN
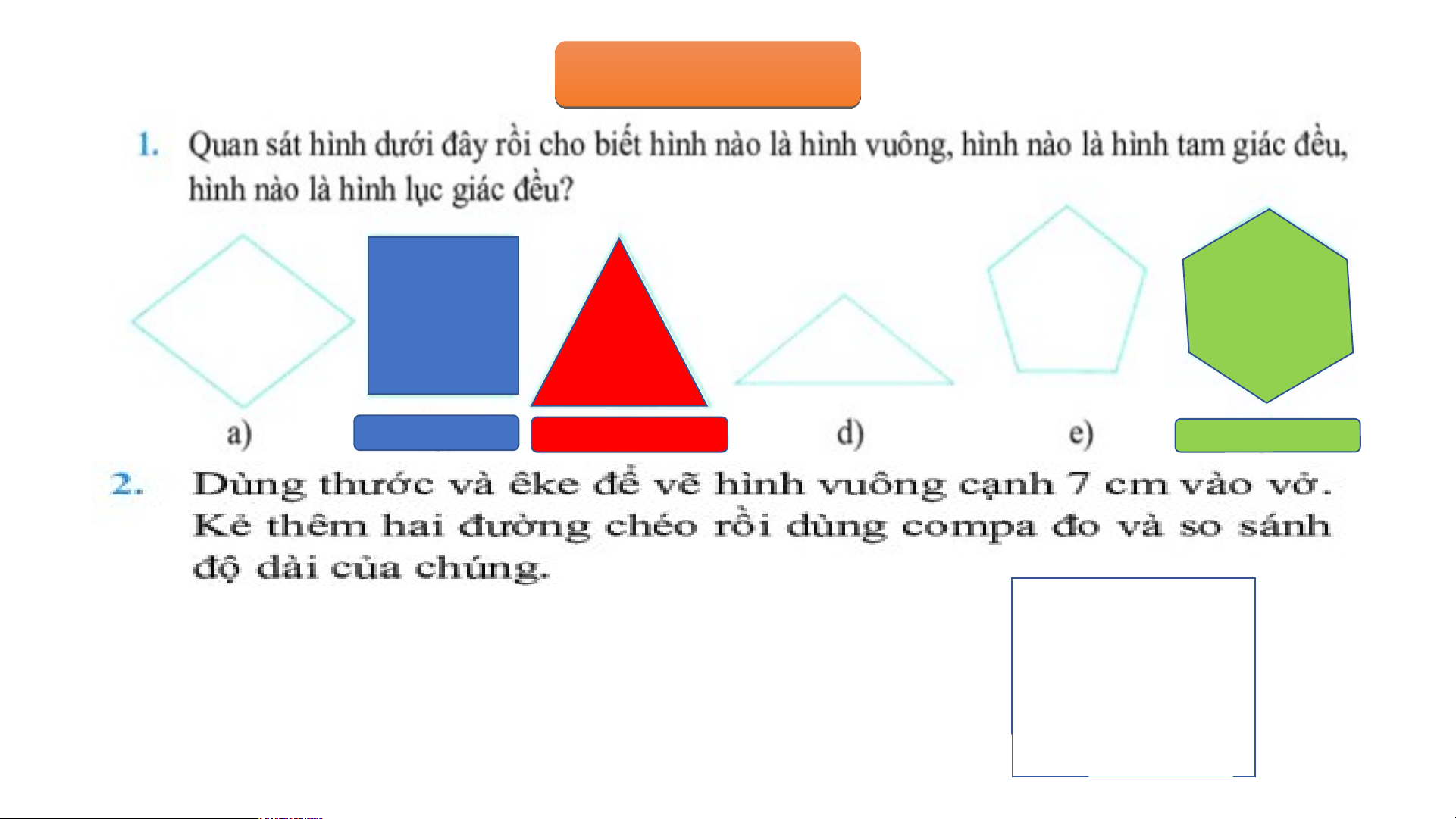
BÀI 18: HÌNH TAM GIÁC ĐỀU, HÌNH VUÔNG, HÌNH LỤC GIÁC ĐỀU
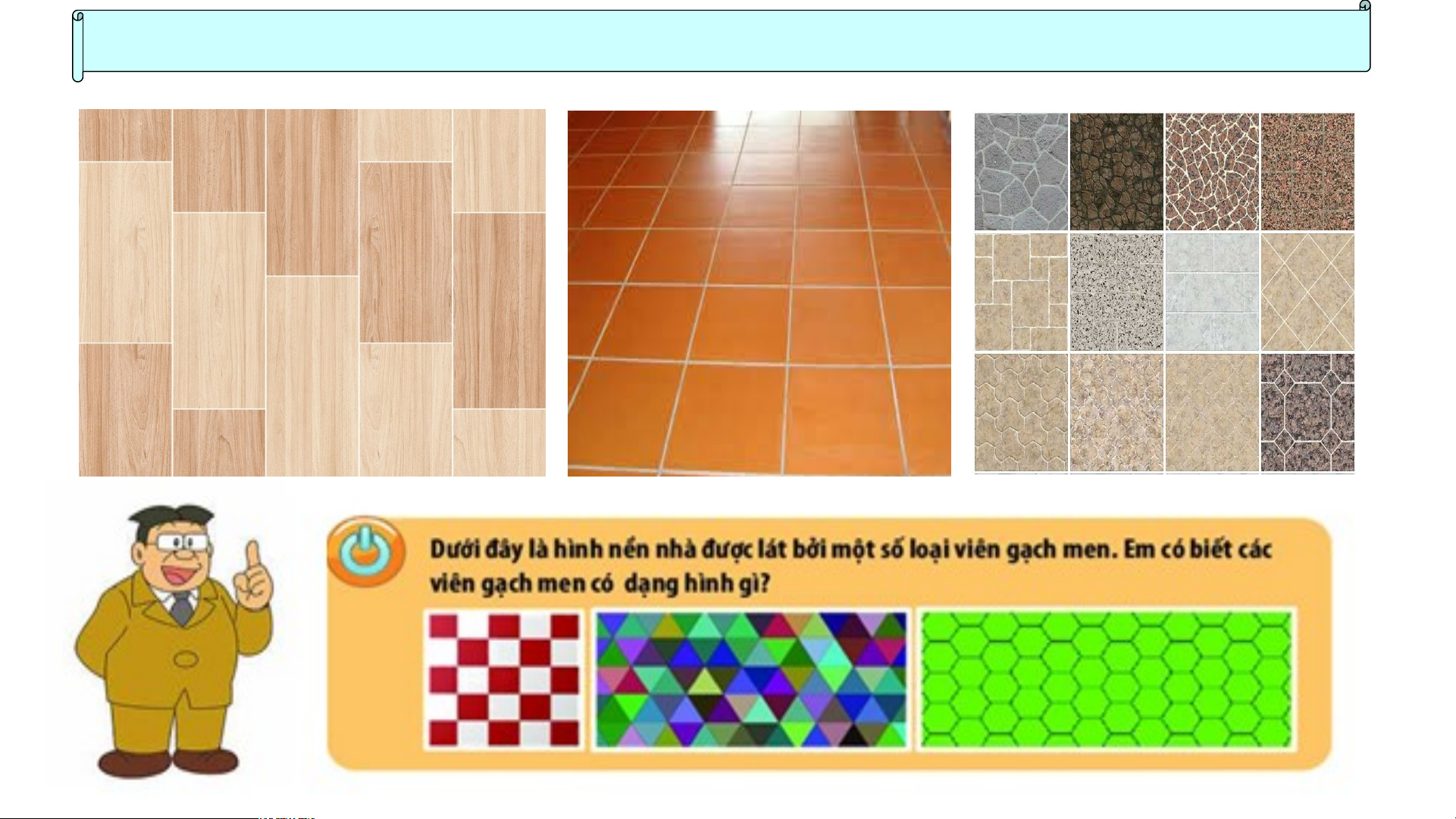
HOẠT ĐỘNG KHỞI ĐỘNG BÀ B I À 1. H 1. Ì H N Ì H N H T A T M A G M I G ÁC Á Đ Ề Đ U Ề , U H , Ì H N Ì H N H V U V Ô U N Ô G N –– H G Ì –– H N Ì H N H L Ụ L C Ụ G C I G ÁC Á C Đ Ề Đ U Ề 1.Tam giác đều Đỉnh Cạnh Góc BÀ B I À 1. H 1. Ì H NH N H T A T M A G M I G ÁC Á C Đ Ề Đ U Ề , U H , Ì H N Ì H N H V U V Ô U N Ô G N , G H , Ì H NH N L H Ụ L C Ụ G C I G Á I C Á Đ C Ề Đ U Ề 1.Tam giác đều
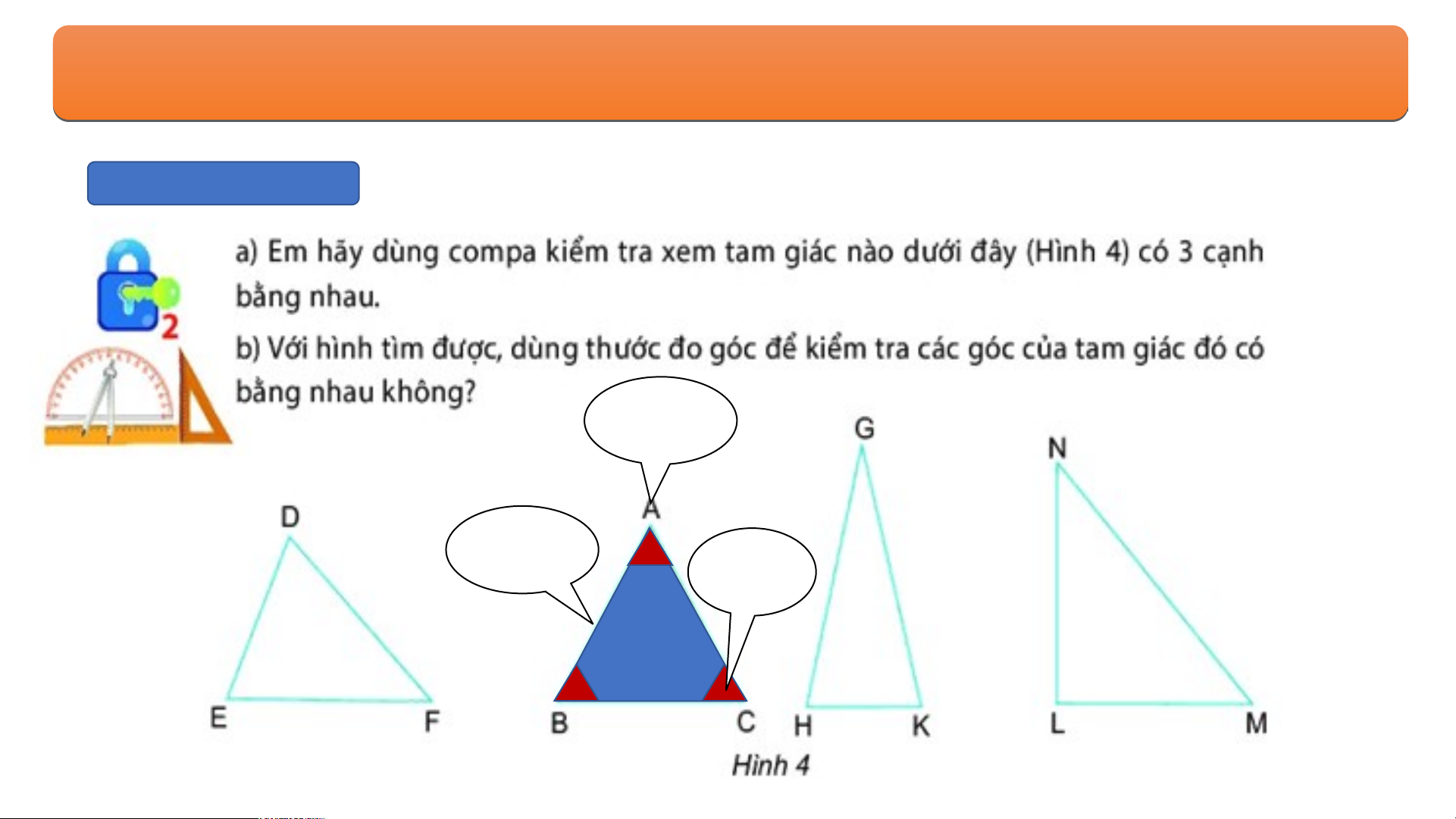
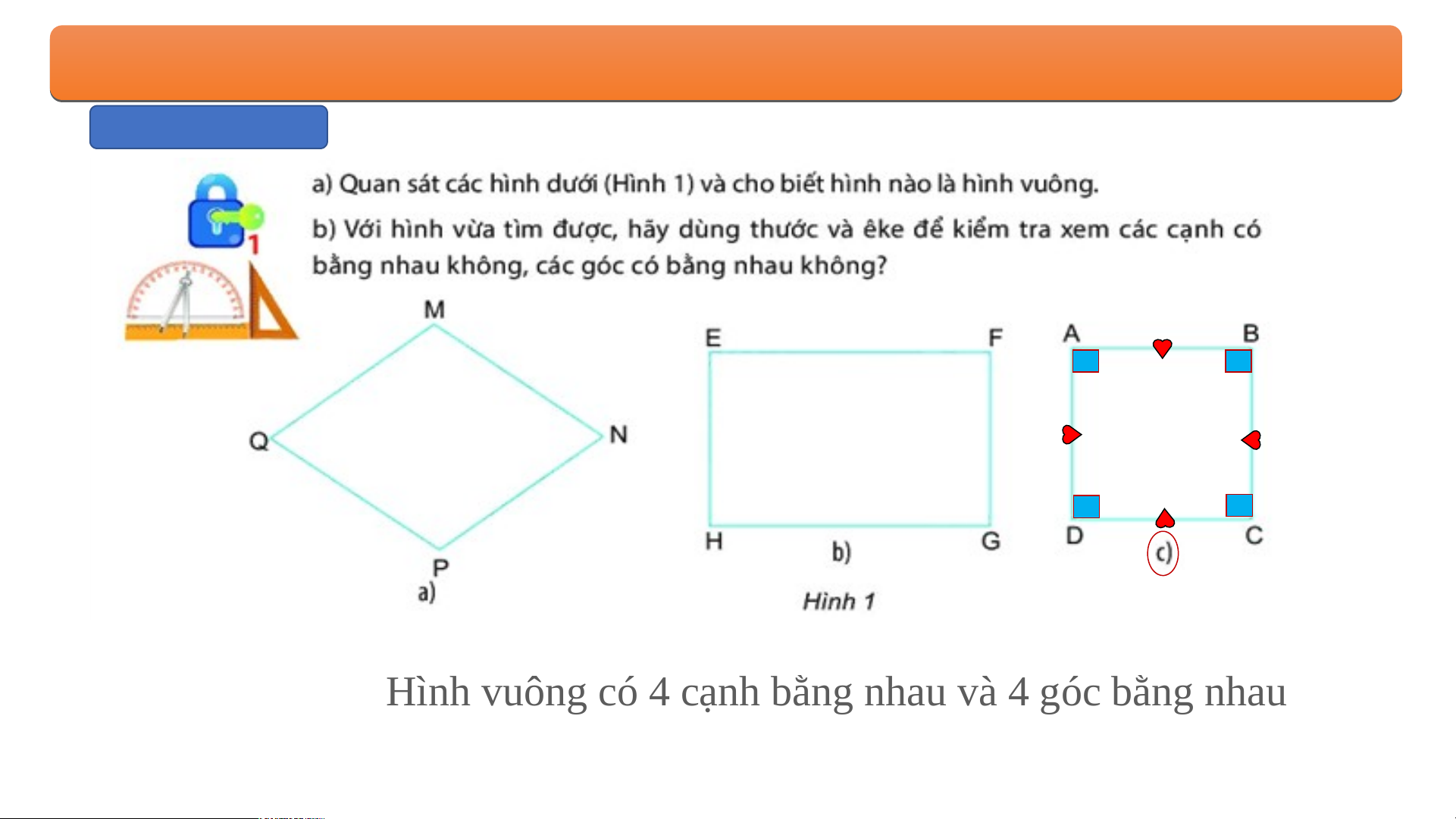
Tam giác có ba cạnh bằng nhau và ba góc bằng nhau gọi là tam giác đều. BÀ B I À 1. H 1. Ì H NH N H T A T M A G M I G Á I C Á C Đ Ề Đ U Ề , U H , Ì H N Ì H N H V U V Ô U N Ô G N , H G Ì , H NH N L H Ụ L C Ụ C G I G Á I C Á Đ C ỀU Đ 1.Tam giác đều BÀ B I À 1 . H . Ì H N Ì H N H T A T M A G M I G ÁC Á Đ C ỀU Đ , ỀU H , Ì H NH N H V U V Ô U N Ô G N , G H , Ì H N Ì H N LỤ H C LỤ G C I G ÁC Á Đ C Ề Đ U Ề 1.Tam giác đều BÀ B I À 1. H Ì 1. H NH N H T A T M A G M I G Á I C Á Đ C ỀU Đ , H ỀU Ì , H NH N V H U V Ô U N Ô G N , G H , Ì H N Ì H N LỤ H C LỤ G C I G ÁC Á C Đ Ề Đ U Ề 2. Hình vuông Hì H nh vuông có g c 4 cạ n cạ h bằng n hau và 4 hau và g óc b óc ằn ằ g nhau BÀ B I À 1. I H 1. Ì H NH N H T A T M A G M I G Á I C Á C Đ Ề Đ U Ề , U H , Ì H N Ì H N H V U V Ô U N Ô G N , H G Ì , H NH N L H Ụ L C Ụ C G I G Á I C Á Đ C ỀU Đ 2. Hình vuông Hì H nh v uông có 4 g có cạnh b ằng ằ nhau và 4 nhau và g óc b óc ằng nhau a . Ha H i a đường đư chéo của h
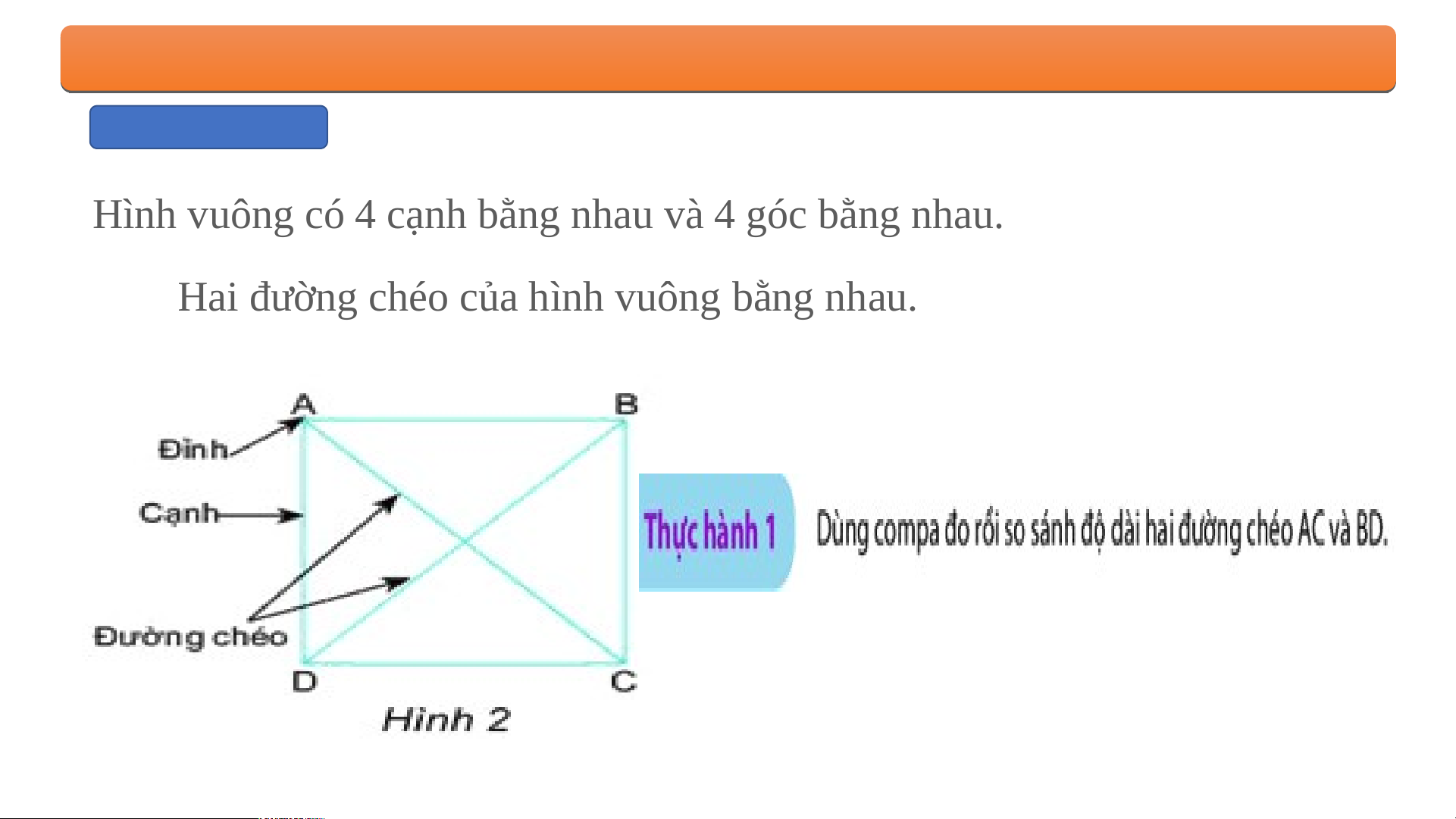
chéo của ình vuông bằng nhau a . BÀ B I À 1. H Ì 1. H NH N H T A T M A G M I G Á I C Á Đ C ỀU Đ , H ỀU Ì , H NH N H V U V Ô U N Ô G N , G H , Ì H NH N L H Ụ L C Ụ G C I G ÁC Á Đ C Ề Đ U Ề 2. Hình vuông Hì H nh v uông có 4 g có cạnh b ằng ằ nhau và 4 nhau và g óc b óc ằng nhau a . Ha H i a đường đư chéo của h
chéo của ình vuông bằng nhau a . SAI BÀ B I À 1 . H . Ì H N Ì H N H T A T M A G M I G ÁC Á Đ C ỀU Đ , ỀU H , Ì H NH N H V U V Ô U N Ô G N , G H , Ì H N Ì H N LỤ H C LỤ G C I G ÁC Á Đ C Ề Đ U Ề 2. Hình vuông Hì H nh v uông có 4 g có cạnh b ằng ằ nhau và 4 nhau và g óc b óc ằng nhau a . Ha H i a đường đư chéo của h
chéo của ình vuông bằng nhau a . BÀ B I À 1. H 1. Ì H NH N H T A T M A G M I G ÁC Á C Đ Ề Đ U Ề , U H , Ì H N Ì H N H V U V Ô U N Ô G N –– G H Ì H N Ì H N H LỤ C LỤ G C I G ÁC Á C Đ Ề Đ U Ề 2. Hình vuông Hì H nh v uông có 4 g có cạnh b ằng ằ nhau và 4 nhau và g óc b óc ằng nhau a . Ha H i a đường đư chéo của h
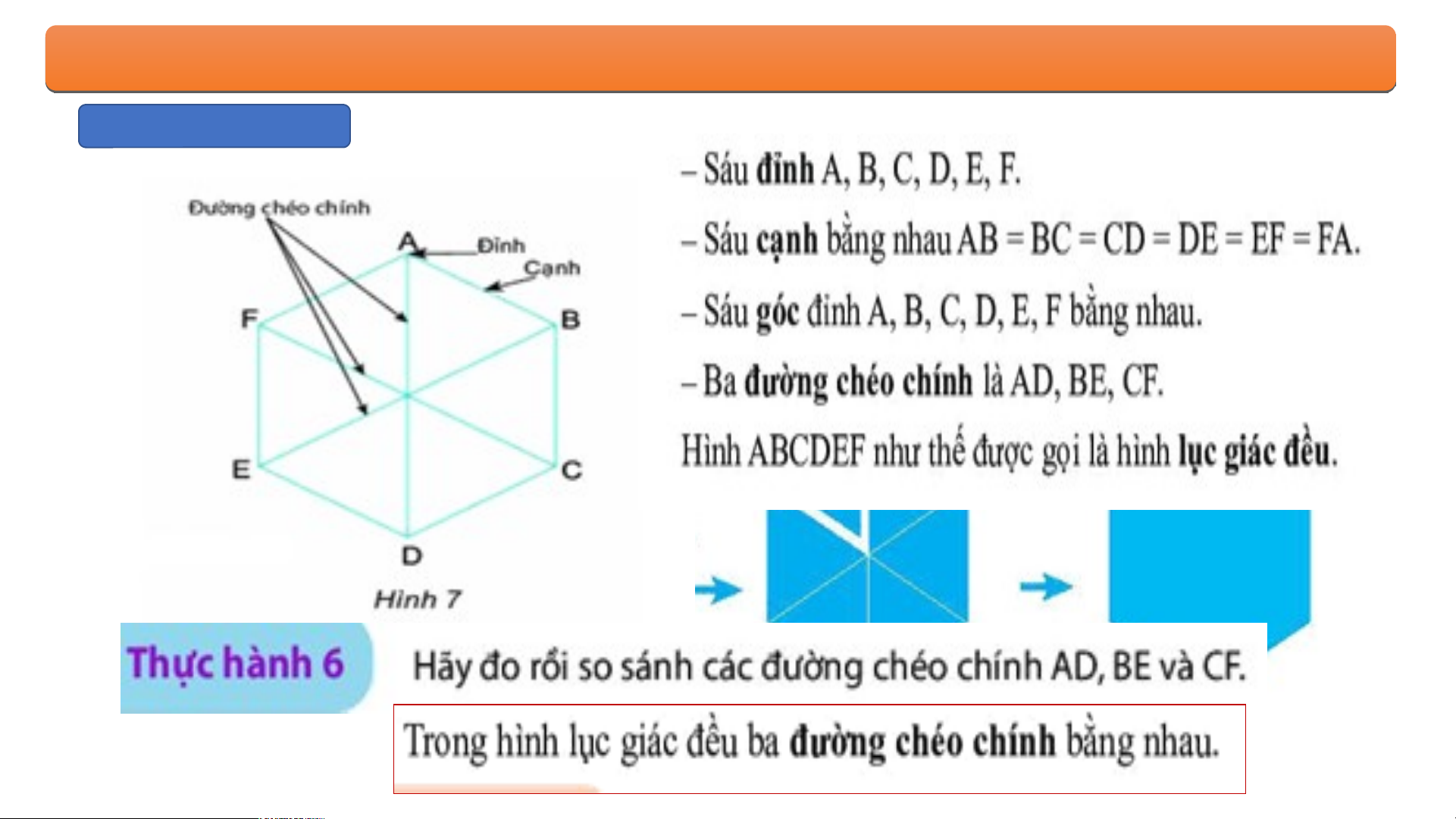
chéo của ình vuông bằng nhau a . BÀ B I À 1. H 1. Ì H NH N H T A T M A G M I G ÁC Á C Đ Ề Đ U Ề , U H , Ì H N Ì H N H V U V Ô U N Ô G N , G H , Ì H NH N L H Ụ L C Ụ G C I G Á I C Á Đ C Ề Đ U Ề 3. Lục giác đều BÀ B I À 1. H 1. Ì H NH N H T A T M A G M I G Á I C Á Đ C Ề Đ U Ề , U H , Ì H NH N H V U V Ô U N Ô G N , G H , Ì H NH N L H Ụ L C Ụ G C I G ÁC Á Đ C ỀU Đ 3. Lục giác đều BÀ B I À 1. H 1. Ì H NH N H T A T M A G M I G Á I C Á C Đ Ề Đ U Ề , U H , Ì H N Ì H N H V U V Ô U N Ô G N , H G Ì , H NH N L H Ụ L C Ụ C G I G Á I C Á Đ C ỀU Đ 3. Lục giác đều BÀ B I À T Ậ T P Ậ Hình vuông Tam giác đều Lục giác đều A B
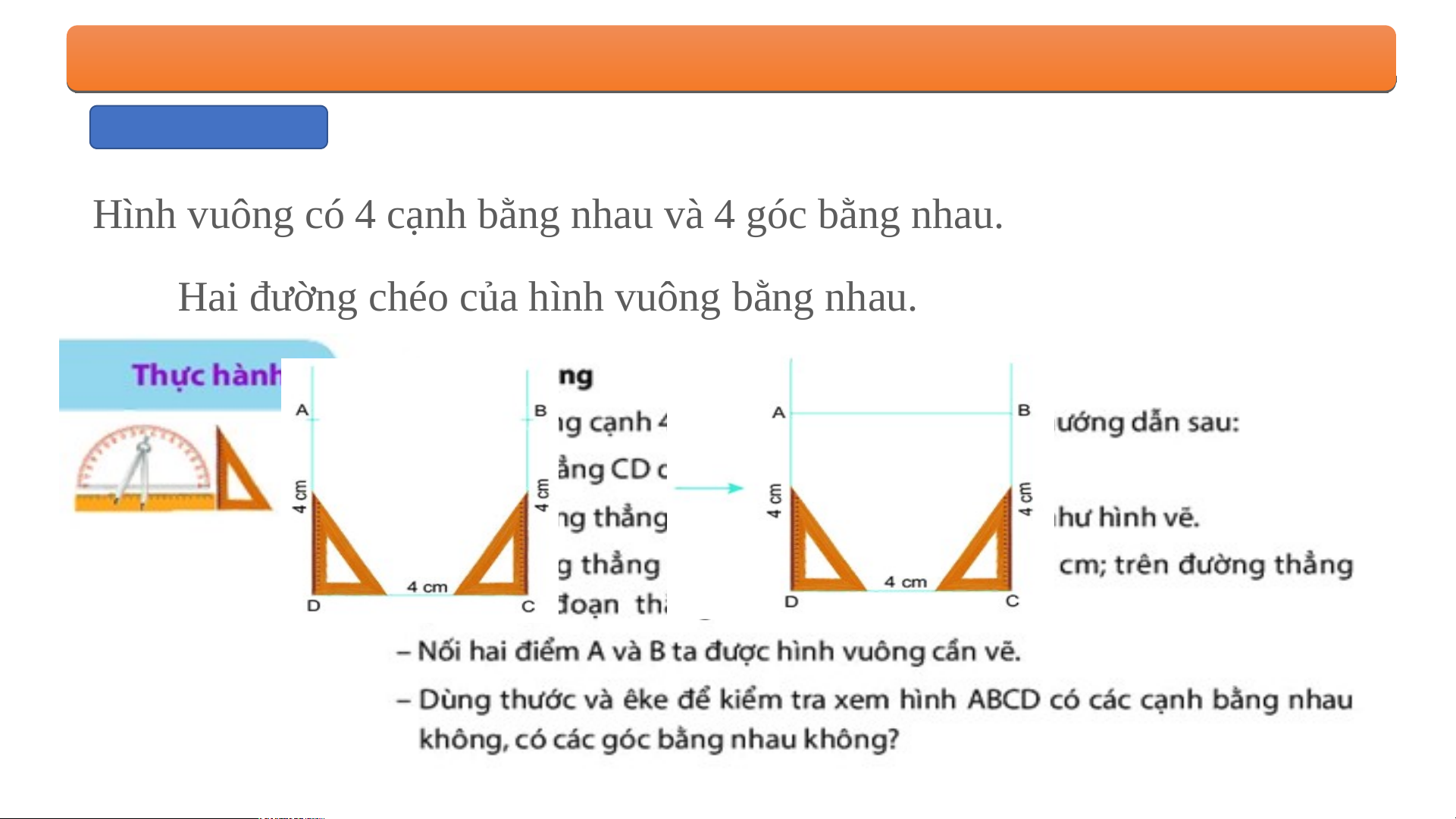
+ Bước 1: Vẽ đoạn thẳng CD = 7cm.
+ Bước 2: Vẽ hai đường thẳng vuông góc với CD tại C và D .
+ Bước 3: Nối hai điểm A và B ta được hình vuông ABCD. 7cm D C BÀ B I À T Ậ T P Ậ Hình vuông
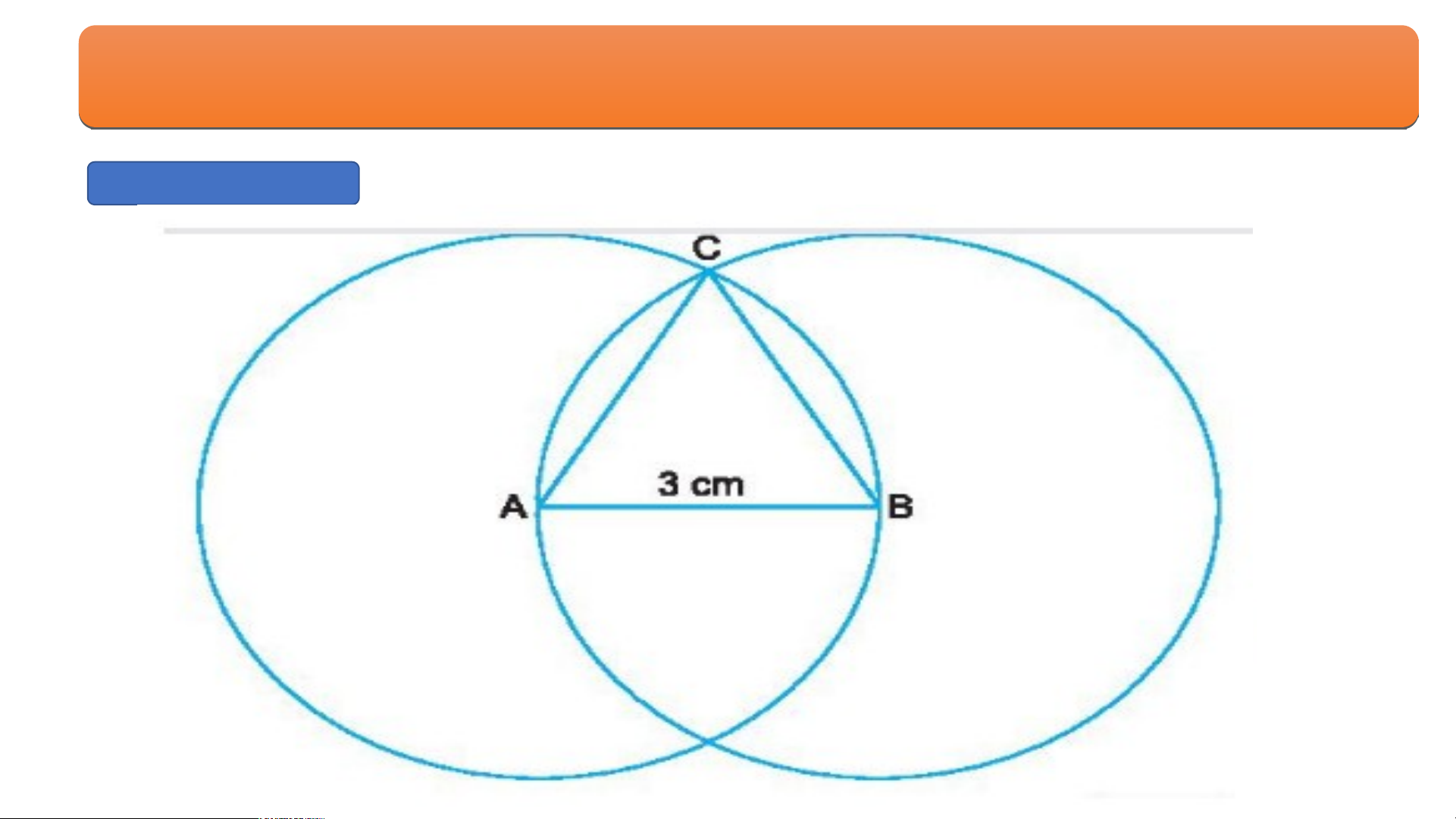
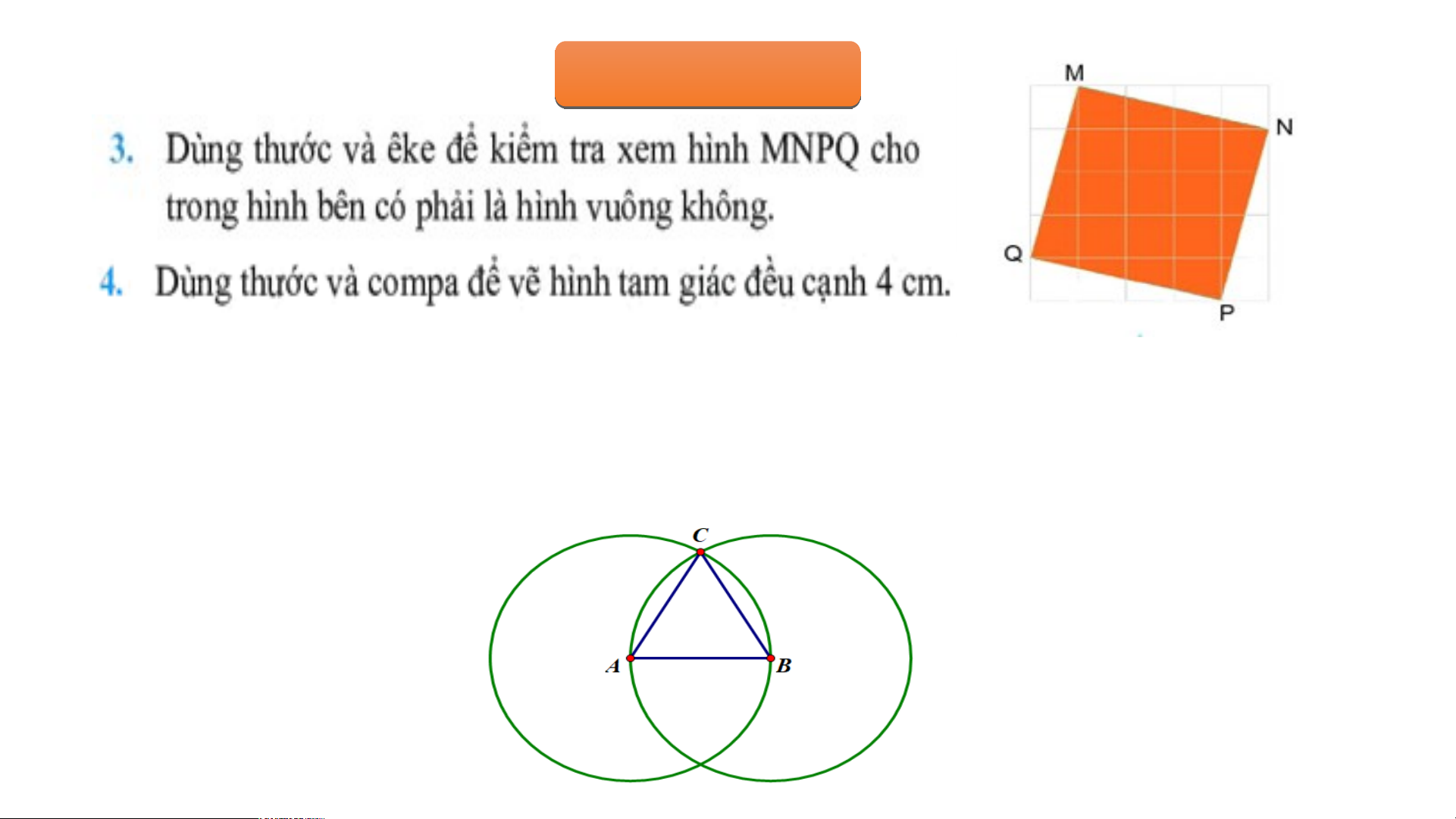
+ Vẽ đoạn thẳng AB = 4cm.
+ Lấy A, B làm tâm, vẽ hai đường tròn bán kính 4cm.
+ Gọi C là một trong hai giao điểm của hai đường tròn. Nối C với A và C với B, ta được tam giác đều ABC. BÀ B I À T Ậ T P Ậ
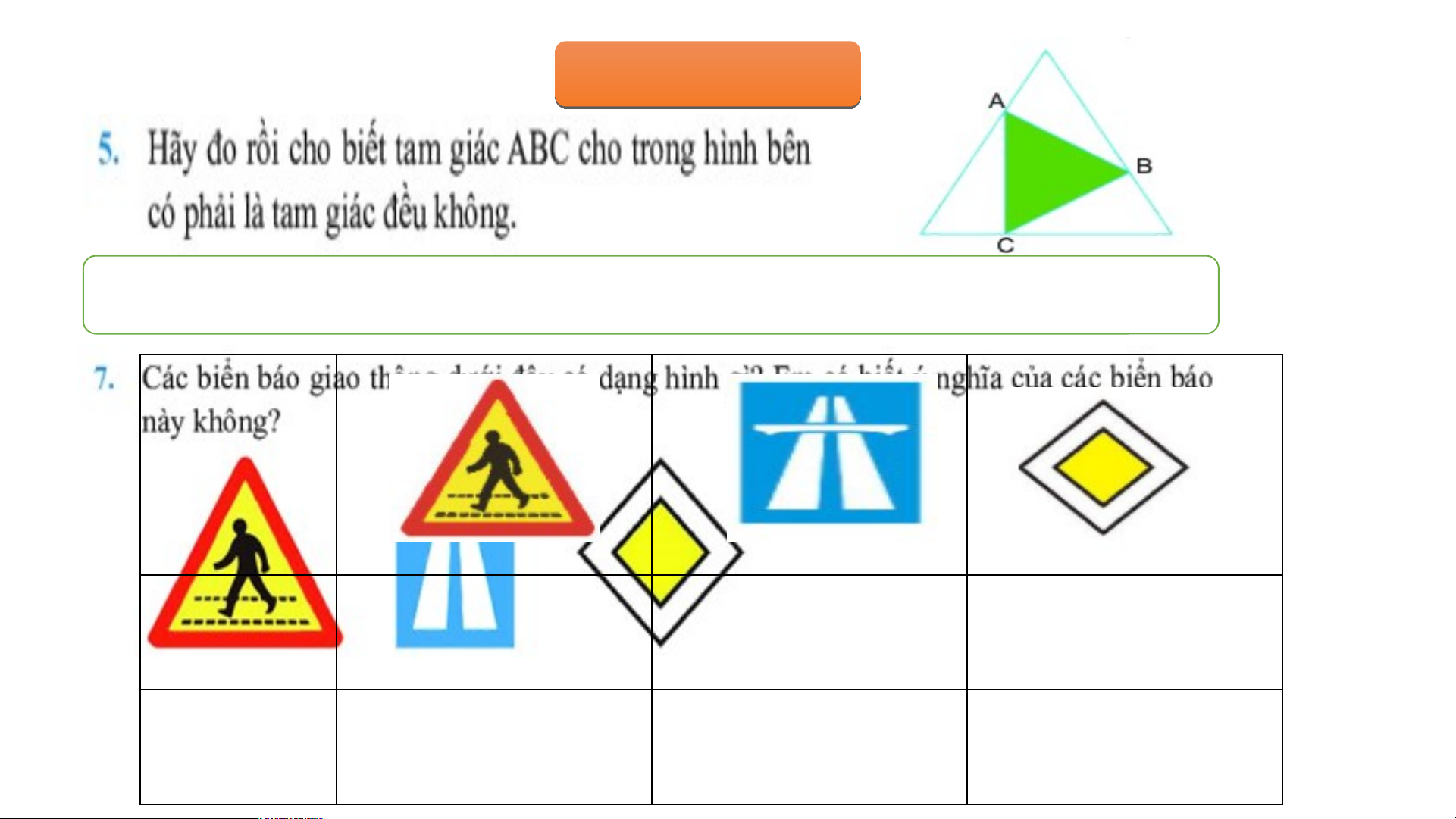
Tam giác ABC là tam giác đều. Bởi vì có các cạnh và các góc bằng nhau. Biển báo Hình dạng Tam giác đều Hình chữ nhật Hình vuông Phần đường người Bắt đầu đường Ý nghĩa Đường cao tốc đi bộ cắt ngang ưu tiên
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20




