Giáo án điện tử Toán 6 Bài 2 Kết nối tri thức: Cách ghi số tự nhiên

Bài giảng PowerPoint Toán 6 Bài 2 Kết nối tri thức: Cách ghi số tự nhiên hay nhất, với thiết kế hiện đại, dễ dàng chỉnh sửa giúp Giáo viên có thêm tài liệu tham khảo để soạn Giáo án Toán 6. Mời bạn đọc đón xem!

15 8 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Bài giảng điện tử Toán 6

Môn: Toán 6

Sách: Kết nối tri thức

Thông tin:

24 trang 3 tháng trước

Tác giả:

Profile Tin Hin



 !!"#
$%!&#
'()( #
*+,-./0%1
*,2#
+34 5 !!"#
5$%!&#
5'()(
*5+,-./0%1
6730879:;
04
<="2#
$="=(#
'()=(>=(?=( #
@-.A:9
B>C
'"4@2=="=(=&=)=>#
DEFE
+@-.A:9B>79
:04
'4@>#

 !"#
$%&'(
)$&$
*+*,-
./0
*12
34*5667
@/G8H:I*J:K-.5:-731L-.
733HM-CN0MM-0HC
$389:;(<"##
O+PHQ5/R-.79:*9S*;
/T*G8MM-U8PH2M-42=="=(=&=)=>=
?= :0<1VPIWM-PH*G8X001
O'Y27Z:V[/T0\7Z:V[0KP9S
31
'];42JP^/=2P^/\1
I*J4-=>=?@ABC
D_/T-.*`MI.0HC
DE
6:-.B89S
1S-.25M-7ab
Pc21
"1D_*d7X57-:S-3-M-P[5
:PbS1eRS0/T3/
M-_bcP1
FGHI L-@JA?=CB>
K);LM$MNO%$P%;LMLM
MNO8;<P%&;LM8MMNOGQP
M;LM'$
L-P34"M-5-3S:0094
NS +f +P \ DZ:V
g0 +P^/
f
'J
f
+f +P^/
P
'J
P
+P +P^/
\
'J
\
\ +P^/ 'J DZ
:V
'M
-
@ J A ? = C B >
Cách phân biệt: Số và chữ số, số chục và chữ số hàng chục, số
trăm và chữ số hàng trăm
I*J4'H-@CBA4
Số đã
cho
Số trăm
Chữ số
hàng trăm
Số chục
Chữ số
hàng chục
Các chữ số
@CBA
( ( < < (= =<=)
R'f*`M-2=:0"G8:Uc-.
3M-1eRM-f:/T1
8#8>S>S>S>
%38;T8U$M9:
L-("2<h/MM-0H5fPPVW
M-U8C
@>BV@W>>>>XW>>>X>W>>XW>XB
-("2<0iPVM-W
31
I*J4""""22O"2O"
"22O"2O"
Y&%ZH[8$HN\H]^8
;T8U$_R
ab
abc
abcd
;
;
với a ≠ 0
ab
a.10 b
abc
a.100 b.10 c
abcd a.1000 b.100 c.10 d
)`9:a;(<"##bc
%ZH[bNde^8;T8U$
_3
jL-.SU3M-0<<<
jL-.SU3M-0
< ?1
*;(<"##M`;(Mf
aT;G8$_8;TNe(R
g&<"#-(&>2&0iPVM-W
31
@J?>JV@W>>>>XJW>>>X?W>>X>W>XJ
F"HI $gH71$f/H;K4H;
a3 /   \ a222 7h5 H; 2 \ a2 222
7h:0H;22\a222227h1+i-Kc
Pc0&<"\7h1/RH;K5/kHA
B < l \  m c Pc H  l K /R H;5 /0
9lAcPc;KbC
JBaJn22OaBn2O
&l22\5<l2\:0"l\7h1
3/g$)Y
'I.
oPVPHQ 2
I
p
1
)
'-NeGA:9B(279:4
j'-NeG:kH3/I.];94L-
&4q=L-<4qp
j'-NeGb7279:944
qqqqqqqqqqqqqqpp
"(&)>? <2
j'-NeGb27"24
q
XI
h h hF hF hF hF hF hh hh
  @ J A ? = C B >
hh hh hh hhF hhF hhF hhF hF hhh hhh
  @ J A ? = C B @>
"Wi
1eR-NeG_*d/T-.iPV
W0:-73
'];4L-ppq300p5p:0q9Z
Y:SPV252:0&1,H73ppq_*d-
"&
"16A3-NeG0H_*d-2
-&:0"?-NeG1
DX-NeGpq5ppqq
j$khFShhF3
%khF)Nl8
hh$MNO$3
+r4L*J7s?BkI5k/79M
-NeG0HC
D4L*J7s?BkI5k/79M-NeG04
pqqqa- 
ppqqqa-"(
ppqa-"&
ppqa-">
ppqpa-"<
-*56
e3?4'H-"?)2=2>?"=?2( )="<)&2&">?
a:PHQ
 DX/R-7GH1
 'M-?PH/R-7GH3PV0HC
8#8
X=A>Hai mươi bảy nghìn năm trăm linh một1
X>?=Một trăm linh sáu nghìn bảy trăm mười hai.
X=>@CABảy triệu một trăm mười nghìn ba trăm tám mươi năm.
XBAJ>J?=Hai tỉ chín trăm mười lăm triệu bốn trăm linh bốn
nghìn hai trăm sáu mươi bảy.
e3='M-&7Y[00HPH/T-.933
PV4
&22&2&
D4
g0P^/
g0J
g07Z:V
e3CDX-NeG4pq=pq=ppqqq1
D4
hFt4e9l-
hFt4e9l
hht4g/9Z1
e3B--NeG4t =")
D4
CmpqqqAmpp
e3>eT-.79:[M-2:0M-<
/km1D30-0HC
D4
L-3M-0HU00P^/\1'M-08
c20P^/\0M-<1+b738P-
\/0B>B>B>1
e3,`M-2=(:0)5:/T-.3M
-/0M-)3PV0)21
D
'M-)3PV)2T0J-7304@A>3
Bn>>>XBn>>XBn>VBBB>auH
e3+PH/T0uH59l733uH
0H;4/R332uH5/RT3235/R`
32T1eT9l/<`5<T:0<3uH1gr9l
737G/UcHuHC
D4
+U8/R332uH5/RT322uHa23:0
/R`3222uH1
9l73/<`5<T:0<3uHi-uH0t4
N\HoKfe
jgXv0kHLo6:S:[7_w/
w-.PHQ5/-
BM0:0PVW/RM-W
-.PHQ5_*d
-NeGb7(21
jDX/J3_k/97__/:K
h-M-:0M-NeG1
jN0/01 j1<PHL$+P<:02
-
'xV0/S4+..PH-.

| 1/24
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

KHỞI ĐỘNG
Câu1 Viết các tập hợp sau bằng cách liệt kê các phần tử a) A = {x N  18 < x < 21} b) B = { x  N*  x < 4 } c) C = { x  N  35  x  38 }
d) Tập hợp D các số tự nhiên x mà x  N* . Ta có: a ,A = {x N  18 < x < 21} b, B = { x  N*  x < 4 } c,C = { x  N  35  x  38
d,Tập hợp D các số tự nhiên x mà x  N*.
Khi đó các tập hợp này được viết lại bằng cách liệt kê các phần tử là: a) A = {19 ; 20} b) B = { 1 ; 2 ; 3 } c) C = { 35 ; 36 ; 37 ; 38 } d) D = {0}
Câu 2:Viết tập hợp E các số tự nhiên x không vượt quá 6 bằng hai cách? ĐÁP ÁN
Tập hợp E các số tự nhiên x không vượt quá 6 được viết bằng hai cách là: Cách 1 : E = {x  N  x   6}
Cách 2 : E = {0 ; 1 ; 2 ; 3 ; 4 ; 5 ; 6}
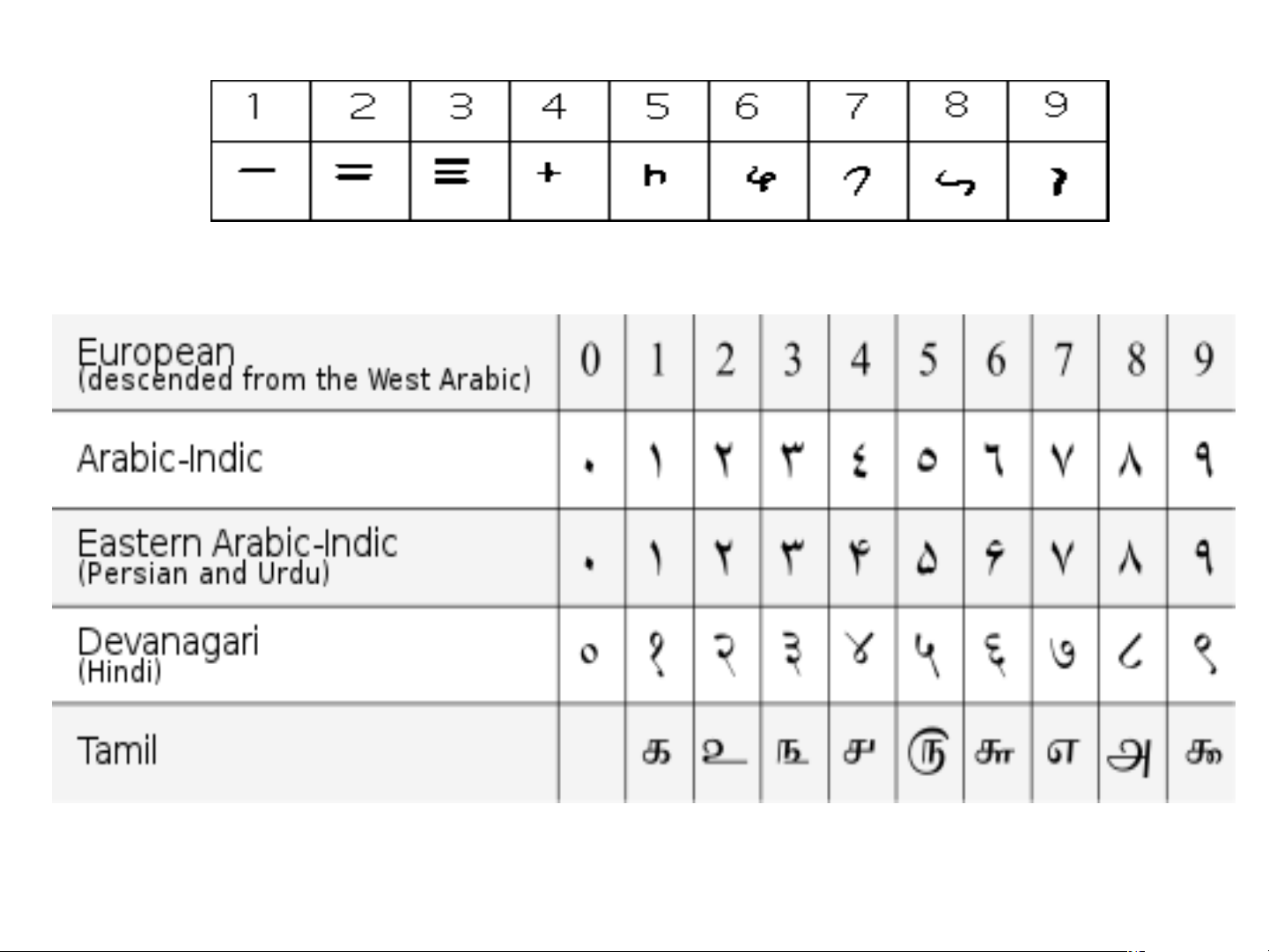
Chữ số Ấn Độ cuối thế kỉ 1
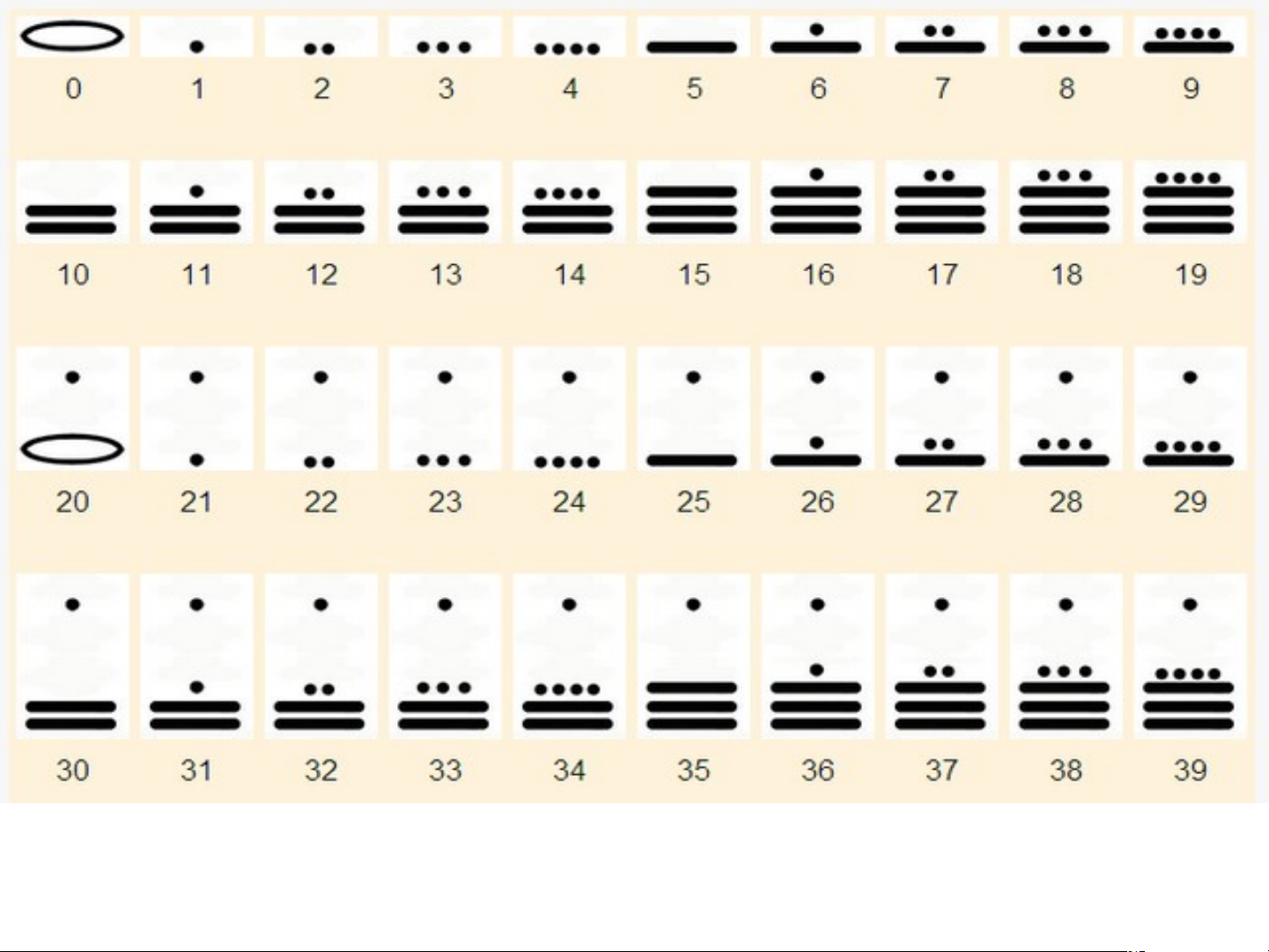
Bảng chữ số Ả Rập Chữ số Babylon Chữ số Maya TIẾT 2- BÀI 2: CÁCH GHI SỐ TỰ NHIÊN 1. HỆ THẬP PHÂN
a. Cách ghi số tự nhiên trong hệ thập phân
+ Trong hệ thập phân, mỗi số tự nhiên được viết dưới dạng
một dãy những chữ số lấy trong 10 chữ số: 0; 1; 2; 3; 4; 5; 6;
7; 8 và 9. Vị trí của các chữ số trong dãy gọi là hàng.
+ Cứ 10 đơn vị ở một hàng thì bằng 1 đơn vị ở hàng liền trước nó.
Em hãy cho ví dụ về số tự nhiên, viết số đó . Số tự
Chẳng hạn: 10 chục = 1 trăm; 10 trăm = 1 nghìn.
nhiên đó có bao nhiêu chữ số ? Là những chữ số nào?
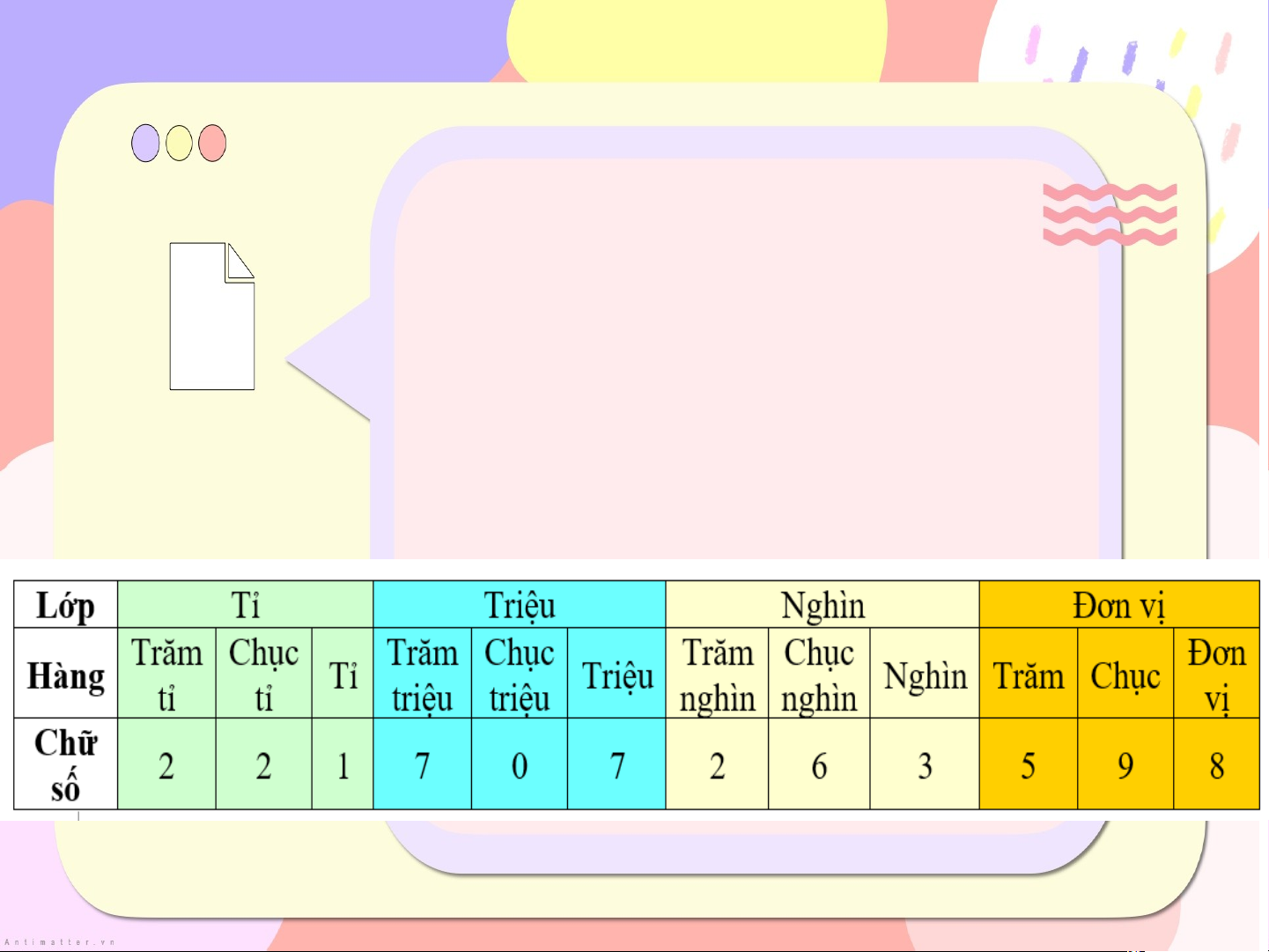
Ví dụ: số 221 707 263 598
Chú ý: Khi viết các số tự nhiên ta quy ước Đ 1. ể g Vớ h i ic mộ ác st ốs ố t ự t ự n nhiê hiên n k ta h d ác ù 0 ng , c h n ữhữ s n ố g đ k ầuí tự tiê nà n o (t ? ừ trái sang phải) khác 0.
2.Để dễ đọc, đối với các số có bốn chữ số trở lên, ta
viết tách riêng từng lớp. Mỗi lớp là một nhóm ba
chữ số kể từ phải sang trái.
Ví dụ: Số 123 456 789 102
Đọc: Một trăm hai mươi ba tỉ, bốn trăm năm
mươi sáu triệu, bảy trăm tám mươi chín nghìn, một trăm linh hai
Số trên có :12 chữ số, số có các lớp và hàng như sau: Lớp Tỉ Triệu Nghìn Đơn vị Hàng Trăm Chục Tỉ
Trăm Chục Triệu Trăm Chục Nghìn Trăm Chục Đơn tỉ tỉ triệu triệu nghìn nghìn vị Chữ số 1 2 3 4 5 6 7 8 9 1 0 2
Cách phân biệt: Số và chữ số, số chục và chữ số hàng chục, số
trăm và chữ số hàng trăm
Ví dụ: Cho số 3895 : Số đã Chữ số Số trăm Chữ số Số chục Các chữ số cho hàng trăm hàng chục 3895 38 8 389 9 3 ; 8 ; 9 ; 5
? Chỉ dùng ba chữ số 0; 1 và 2 hãy viết tất cả các số tự
nhiên có ba chữ số. Mỗi chữ số chỉ viết một lần.
Đáp án: 120; 210; 102; 201
b. Giá trị các chữ số của một số tự nhiên
HĐ1: Số 32019 gồm những chữ số nào, chỉ ra giá trị của các chữ số ấy?
HĐ2: Viết số 32019 thành tổng giá trị các chữ số của 32
nó. 019 = 3 x10000 + 2 x1000 + 0 x100 + 1 x 10 + 9 Ví dụ : 222 = 200 + 20 + 2 = 2 x 100 + 2 x 10 + 2
Hãy biểu diễn các số sau dưới dạng tổng giá
trị các chữ số của nó ? ab ; ; với a ≠ 0 abc abcd ab  a.10  b abc  a.100  b.10  c
abcd a.1000  b.100  c.10  d
Mỗi số tự nhiên viết trong hệ thập phân đều
biểu diễn được thành tổng giá trị các chữ số của nó.
- Số tự nhiên lớn nhất có ba chữ số là 999
- Số tự nhiên lớn nhất có ba chữ số khác nhau là 987 .
Trong hệ thập phân mỗi chữ số trong một số ở
những vị trí khác nhau có giá trị như thế nào?
Luyện tập: Viết số 34604 thành tổng giá trị các chữ số của
nó. 34604 = 3 x 10000 + 4 x 1000 + 6 x 100 + 0 x10 + 4
Vận dụng: Bác Hoa đi chợ. Bác chỉ mang ba loại tiền: loại
(có mệnh giá) 1 nghìn (1000) đồng, loại 10 nghìn (10 000)
đồng và loại 100 nghìn (100 000) đồng. Tổng số tiền bác phải
trả là 492 nghìn đồng. Nếu mỗi loại tiền, bác mang theo không
quá 9 tờ thì bác sẽ phải trả bao nhiêu tờ tiền mỗi loại, mà
người bán không phải trả lại tiền thừa?
492 = (4 × 100) + ( 9 × 10) + 2
4 tờ 100 nghìn, 9 tờ 10 nghìn và 2 tờ 1 nghìn đồng. 2 . Số La Mã
Các số La Mã không vượt quá 30 được viết sau : Các kí tự I I V X
Giá trị trong hệ thập phân 1 5 10 1
- Các số La Mã viết theo nhóm kí tự chẳng hạn như: Số 4:IV ; Số 9: IX
- Các số La Mã từ 1 đến 10 được viết như sau: :
I II III IV V VI VII VIII IX X 1 2 3 4 5 6 7 8 9 10
- Các số La Mã từ 10 đến 20:
XI XII XIII XIV XV XVI XVII XVIII XIX XX 11 12 13 14 15 16 17 18 19 20 XXI XXII XXIII XXIV XXV XXVI XXVII XVIII XXIX XXX 21 22 23 24 25 26 27 28 29 30 Nhận xét:
1.Mỗi số La Mã biểu diễn một số tự nhiên bằng tổng giá trị
của các thành phần viết nên số đó
Chẳng hạn: Số XXIV có ba thành phần là X, X và IV tương
ứng với các giá trị 10, 10 và 4. Do đó XXIV biểu diễn số 24
2. Không có số La Mã nào biểu diễn số 0
a) Viết các số 14 và 27 bằng số La Mã.
b) Đọc các số La Mã XVI, XXII ĐA a) XIV; XXVII. b) XVI: Mười sáu XXII: Hai mươi hai.
Thử thách nhỏ :Sử dụng đúng 7 que tính, em xếp được những số La Mã nào?
ĐA:Sử dụng đúng 7 que tính, em xếp được những số La Mã là: XVIII ( số 18) XXIII ( số 23) XXIV ( số 24) XXVI ( số 26) XXIX ( số 29) BÀI TẬP
Bài 1.6: Cho các số 27 501; 106 712; 7 110 385; 2 915 404 267
(viết trong hệ thập phân) a) Đọc mỗi số đã cho.
b) Chữ số 7 trong mỗi số đã cho có giá trị là bao nhiêu? Đáp án:
+ 27 501: Hai mươi bảy nghìn năm trăm linh một.
+ 106 712: Một trăm linh sáu nghìn bảy trăm mười hai.
+ 7 110 385: Bảy triệu một trăm mười nghìn ba trăm tám mươi năm.
+ 2 915 404 267: Hai tỉ chín trăm mười lăm triệu bốn trăm linh bốn
nghìn hai trăm sáu mươi bảy.
Bài 1.7: Chữ số 4 đứng ở hàng nào trong một số tự nhiên nếu như nó có giá trị bằng: a) 400 b) 40 c) 4 Đáp án: a) Hàng trăm b) Hàng chục c) Hàng đơn vị
Bài 1.8: Đọc các số La Mã: XIV; XVI; XXIII. Đáp án: XIV : Mười bốn XVI : Mười sáu XXIII : Hai mươi ba.
Bài 1.9: Viết các số sau bằng số La Mã: 18; 25 Đáp án:
18 : XVIII 25 : XXV
Bài 1.10: Một số tự nhiên được viết bởi ba chữ số 0 và ba chữ số 9
nằm xen kẽ nhau. Đó là số nào? Đáp án:
Số có sáu chữ số nên hàng cao nhất là hàng trăm nghìn. Chữ số này
phải khác 0 nên hàng trăm nghìn là chữ số 9. Từ đó suy ra số cần tìm là 909 090.
Bài 1.11: Dùng các chữ số 0; 3 và 5, viết một số tự nhiên có ba chữ
số khác nhau mà chữ số 5 có giá trị là 50. Đáp án:
Chữ số 5 có giá trị 50 nên thuộc hàng chục  số đó là: 350.
Bài 1.12: Trong một cửa hàng bánh kẹo, người ta đóng gói kẹo
thành các loại: mỗi gói có 10 cái kẹo, mỗi hộp có 10 gói, mỗi thùng
có 10 hộp. Một người mua 9 thùng, 9 hộp và 9 gói kẹo. Hỏi người
đó đã mua tất cả bao nhiêu cái kẹo? Đáp án:
Ta thấy mỗi gói có 10 cái kẹo, mỗi hộp có 100 cái kẹo (10 gói) và
mỗi thùng có 1000 cái kẹo.
Người đó mua 9 thùng, 9 hộp và 9 gói kẹo nên tổng số kẹo là :
9 × 1000 + 9 × 100 + 9 × 10 = 9 990 (cái kẹo)
Hướng dẫn học ở nhà
- Học kỹ bài theo SGK kết hợp với vở ghi để nắm
chắc cách ghi số tự nhiên trong hệ thập phân, mối
quan hệ giữa các hàng và giá trị của mỗi chữ số của
số tự nhiên trong hệ thập phân, cách biểu diễn các số La Mã từ 1 đến 30.
- Đọc mục có thể em chưa biết để hiểu biết thêm về
nguồn gốc các chữ số và chữ số La Mã.
- Làm bài tập 1.8 -1.19 trong SBT trang 9 và 10
- Chuẩn bị bài mới: Thự tự trong tập hợp các số tự nhiên
Document Outline

  • Slide 1
  • Slide 2
  • Slide 3
  • Slide 4
  • Slide 5
  • Slide 6
  • Slide 7
  • Slide 8
  • Slide 9
  • Slide 10
  • Slide 11
  • Slide 12
  • Slide 13
  • Slide 14
  • Slide 15
  • Slide 16
  • Slide 17
  • Slide 18
  • Slide 19
  • Slide 20
  • Slide 21
  • Slide 22
  • Slide 23
  • Slide 24