Giáo án điện tử Toán 6 Bài 23 Kết nối tri thức: Mở rộng phân số. Phân số bằng nhau

Bài giảng PowerPoint Toán 6 Bài 23 Kết nối tri thức: Mở rộng phân số. Phân số bằng nhau hay nhất, với thiết kế hiện đại, dễ dàng chỉnh sửa giúp Giáo viên có thêm tài liệu tham khảo để soạn Giáo án Toán 6. Mời bạn đọc đón xem!

22 11 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Bài giảng điện tử Toán 6

Môn: Toán 6

Sách: Kết nối tri thức

Thông tin:

32 trang 3 tháng trước

Tác giả:

Profile Tin Hin


BÀI 23: MỞ RỘNG
KHÁI NIỆM PHÂN SỐ.
PHÂN SỐ BẰNG NHAU
(tiết 1)
CHƯƠNG VI – PHÂN SỐ
Tiết 46 + 47 - BÀI 23:
MỞ RỘNG KHÁI NIỆM PHÂN SỐ.
PHÂN SỐ BẰNG NHAU
KHỞI ĐỘNG
Với a,b N, b ≠ 0, ta gọi là một phân số. Trong đó
a là tử số (tử), b là mẫu số (mẫu) của phân số
a
b
Tương tự ta cũng gọi là phân số,
Ví dụ:
Ta có :
là phân số
2
5
21
;
5
2
;.....
5
Luyện tập 1;
Viết kết quả phép chia sau dưới dạng phân số
a) 4 : 9 b) (-2) : 7 c) 8 : (-3)
a ¿
4
9
b ¿
−2
7

Kết quả
Nhận xét:
Số nguyên a có thể viết dưới dạng phân số là
Ví dụ:
1
a
a
3
3
1
=
HĐ 2
Trả lời
HĐ 3

1
3
¿
3
9
2
5
3
4
6
8
HĐ 4
Trả lời
HĐ 3

1
3
¿
3
9
2
5


Quy tắc bằng nhau của hai phân số nếu a.d = b.c
Ví dụ 1
Ta có:
Vì (-9) . 4 = 12 . (-3) ( cùng bằng -36)
Luyện tập 2:
Các cặp phân số sau đây có bằng nhau không?
Vì (-3) . (-15) = 5 . 9 (cùng bằng 45)
Vì (-1) . 4 = (-4) . 1 (cùng bằng 4)
Trả lời
a c
b d
9 3
12 4
3 9
)
5 15
a
1 1
)
4 4
b
Ví dụ : Tìm số nguyên x, biết:
Giải:
Vì nên x . 28 = 4.21
Vậy x = 3
x 21
4 28
x 21
4 28
4.21
x 3
28
1. Với a,b Z, b ≠ 0, ta gọi là một phân số. Trong đó
a là tử số (tử), b là mẫu số (mẫu) của phân số
2. Quy tắc bằng nhau của hai phân số nếu a.d = b.c
Ghi nhớ
a
b
a c
b d
-
Học thuộc khái niệm phân số và định nghĩa hai phân
số bằng nhau.
-
Luyện tập cách kiểm tra phân số và hai phân số
bằng nhau.
-
Luyện tập bài tìm số chưa biết.
-
Làm bài tập 6.1; 6.2. 6.3 SGK – Tr 8
!
"
BT2
#
BT3
BT1
Mọi số nguyên có thể viết dưới dạng phân số
không? Cho ví dụ.
Cho 3 ví dụ về phân số. Cho biết tử và mẫu của
mỗi phân số đó.
?1
… là những phân số.
BT2


Trong các cách viết sau đây, cách viết nào cho
ta phân số
Nhận xét: số nguyên a có thể viết
Chẳng hạn như
BT3
Mọi số nguyên đều viết được dưới dạng phân số.
4
7
0, 25
3
2
5
6, 23
7, 4
3
0
-2 3 1 -1 0
, , , , ,
3 -5 4 -2 -3
4
7
2
5
1
a
a
3
3
1
2 5
2 , -5
1 1
$%&'()
$%&'()
Ví Dụ 2
Chú ý: Mọi phân số đều có thể viết dưới dạng phân số có mẫu dương
- Người ta thường dùng tính chất 2 để rút gọn phân số.
2 2.( 3) 6
5 ( 5).( 3) 15
12 ( 12) : 4 3
16 16 : 4 4
$%&'()
Có nhiều cách đi,
Việt có thể đi như
sau: .
$%&'()
*+,
Câu 1: Hai phân số và bằng
nhau nếu ………………….
m.h = n.e
m
n
e
h
*+,
Câu 2: Nếu thì x bằng:
Đáp số:
x.6 = - 12. (- 4)
x.6 = 48
x = 48 : 6
x = 8
12
4 6
x
*+,
Câu 3: Cặp số bằng nhau là :
ĐÁP ÁN : Câu c
6 5
) à
5 6
a v
3 9
) à
4 12
b v
2 20
) à
3 30
c v
2 2
) à
3 3
d v
*+,
Câu 4: Nếu x là số nguyên âm
và : thì x =….
A / 10 C / -25B / -5
D / 25
ĐÁP ÁN: Câu B
5
5
x
x
Giải
Vì
nên x . 21 = 7 . (6)
Suy ra
Tìm số nguyên x, biết
x
7
6
21
=
Bài 6
a.
6
7 21
x
7.(6) 42
2
21 21
x
Giải:
Tìm số nguyên y, biết:
-5
y
20
28
=
-5
y
20
28
=
Vì
nên -5 . 28 = y . 20
hay y . 20 = -5 . 28
Suy ra y =
b.
5.28
7
20
$%&'()-./01231%/45167891/:;2<'=7)
!
"
BT2
#
BT3
BT1
Mọi số nguyên có thể viết dưới dạng phân số
không? Cho ví dụ.
Cho 3 ví dụ về phân số. Cho biết tử và mẫu của
mỗi phân số đó.
?1
… là những phân số.
BT2


Trong các cách viết sau đây, cách viết nào cho
ta phân số
Nhận xét: số nguyên a có thể viết
Chẳng hạn như
BT3
Mọi số nguyên đều viết được dưới dạng phân số.
4
7
0, 25
3
2
5
6, 23
7, 4
3
0
-2 3 1 -1 0
, , , , ,
3 -5 4 -2 -3
4
7
2
5
1
a
a
3
3
1
2 5
2 , -5
1 1
-
Học thuộc khái niệm phân số và định nghĩa hai phân
số bằng nhau.
-
Luyện tập cách kiểm tra phân số và hai phân số
bằng nhau.
-
Luyện tập bài tìm số chưa biết.
-
Làm bài tập 5; 7; 8; 9; 10/SGK – Tr6,8,9
và Bài 6, 7, 8, 14, 15, 16, 17/SBT – Tr6,7
| 1/32
| | Tải xuống

Có thể bạn quan tâm:

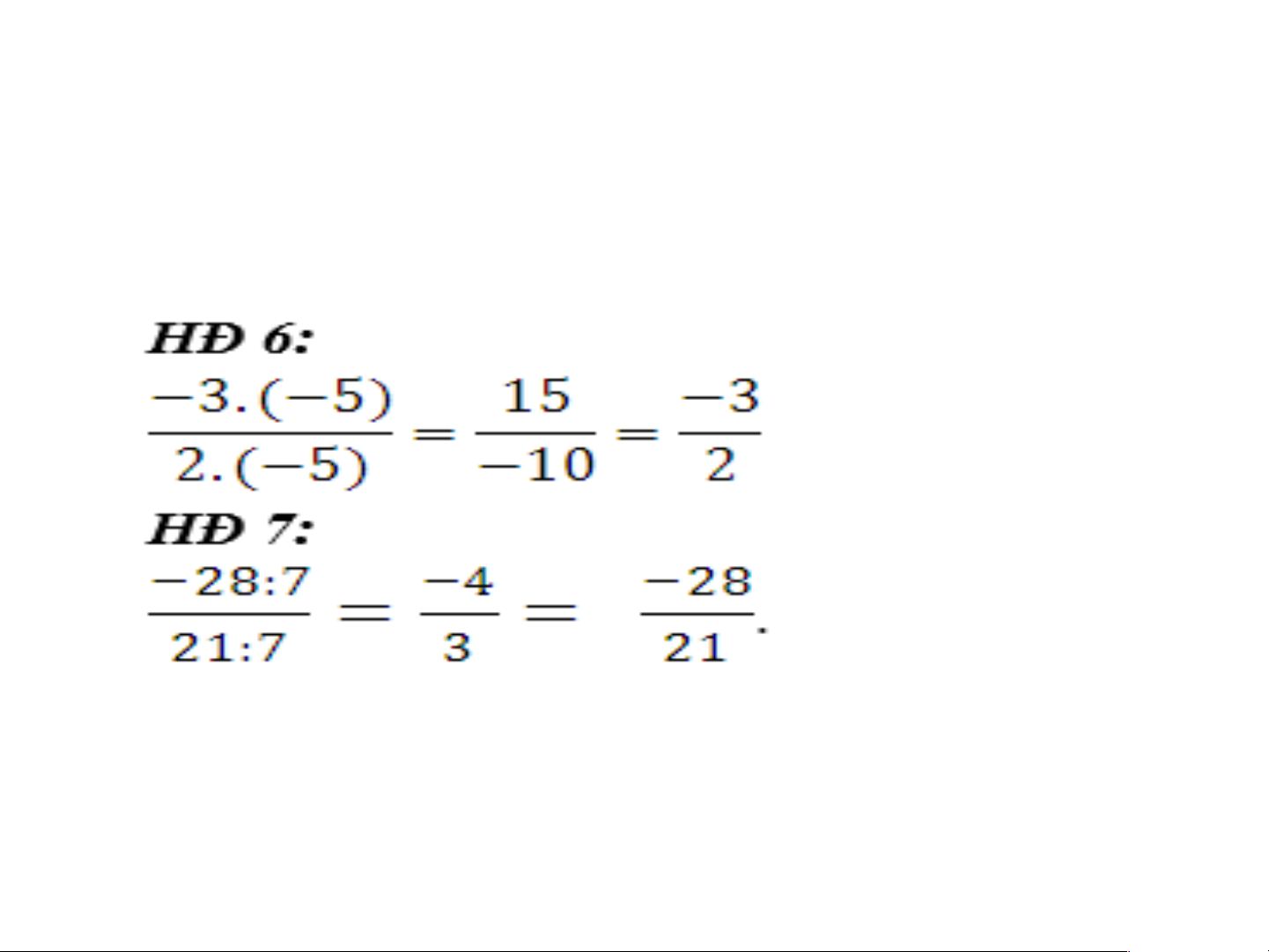
Preview text:

BÀI 23: MỞ RỘNG
KHÁI NIỆM PHÂN SỐ. PHÂN SỐ BẰNG NHAU (tiết 1)
BỘ SÁCH KẾT NỐI TRI THỨC VỚI CUỘC SỐNG
CHƯƠNG VI – PHÂN SỐ
Tiết 46 + 47 - BÀI 23:
MỞ RỘNG KHÁI NIỆM PHÂN SỐ. PHÂN SỐ BẰNG NHAU KHỞI ĐỘNG a Với a,b 
N, b ≠ 0, ta gọi là một phân số. Trong đó b
a là tử số (tử), b là mẫu số (mẫu) của phân số Ta có : là phân số
Tương tự ta cũng gọi  l 2 à phân số, 5 Ví dụ: 2  21; ;..... 5  5 Luyện tập 1;
Viết kết quả phép chia sau dưới dạng phân số
a) 4 : 9 b) (-2) : 7 c) 8 : (-3) Kết quả 4 −2 a c) ¿ b 9 ¿ 7 Nhận xét: a
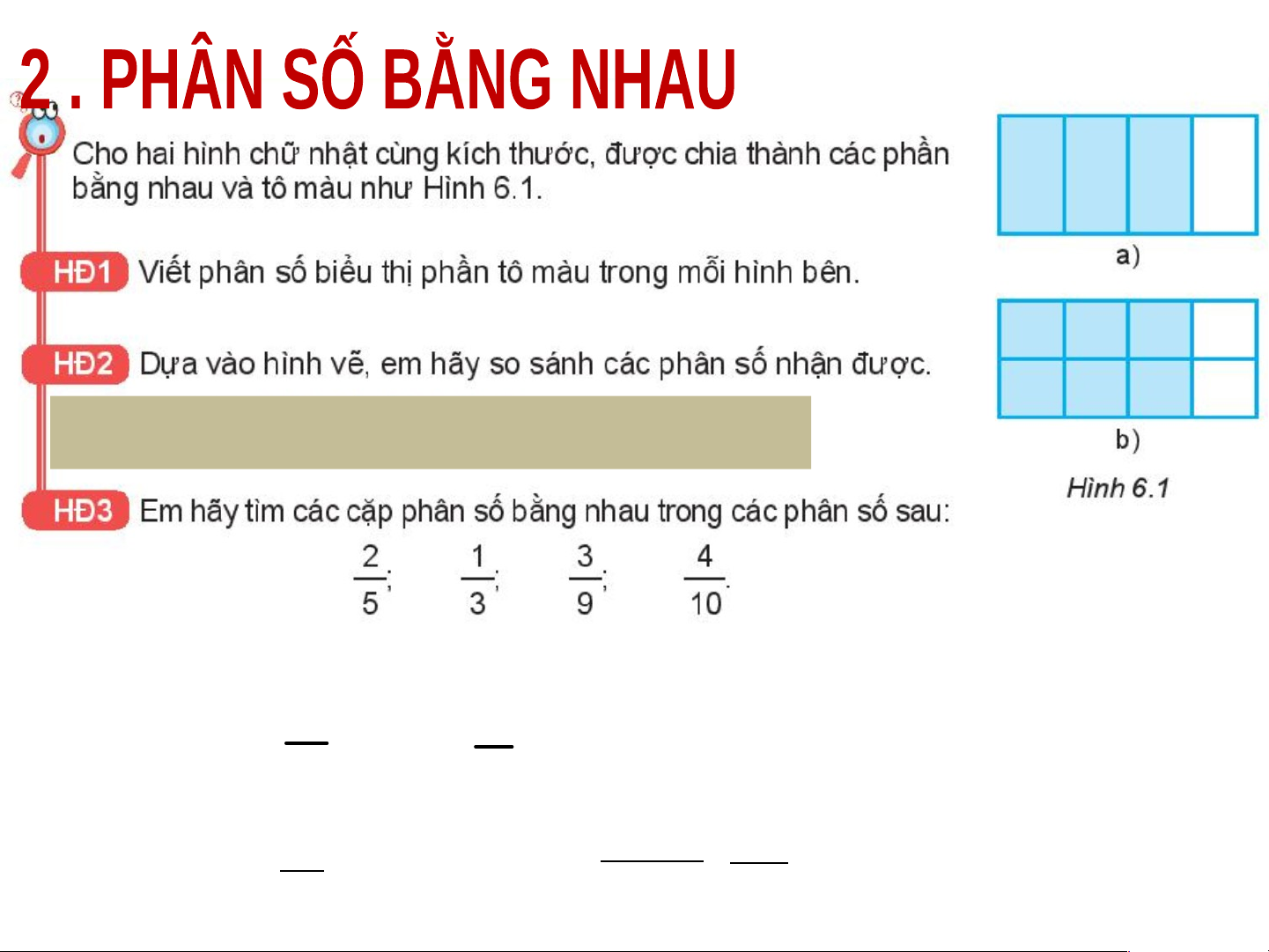
Số nguyên a có thể viết dưới dạng phân số là a 1  3 Ví dụ:  3  1 Trả lời 3 HĐ 2 6 4 = 8 HĐ 3 1 3 2 = 3 ¿ 9 5 1 HĐ 3 3 2 = 3 ¿ 9 5 Trả lời HĐ 4 2. 10 = 4.5 1.9 = 3.3 a c
Quy tắc bằng nhau của hai phân số nế  u a.d = b.c b d Ví dụ 1  9  3 Ta có: 
Vì (-9) . 4 = 12 . (-3) ( cùng bằng -36) 12 4 Luyện tập 2:
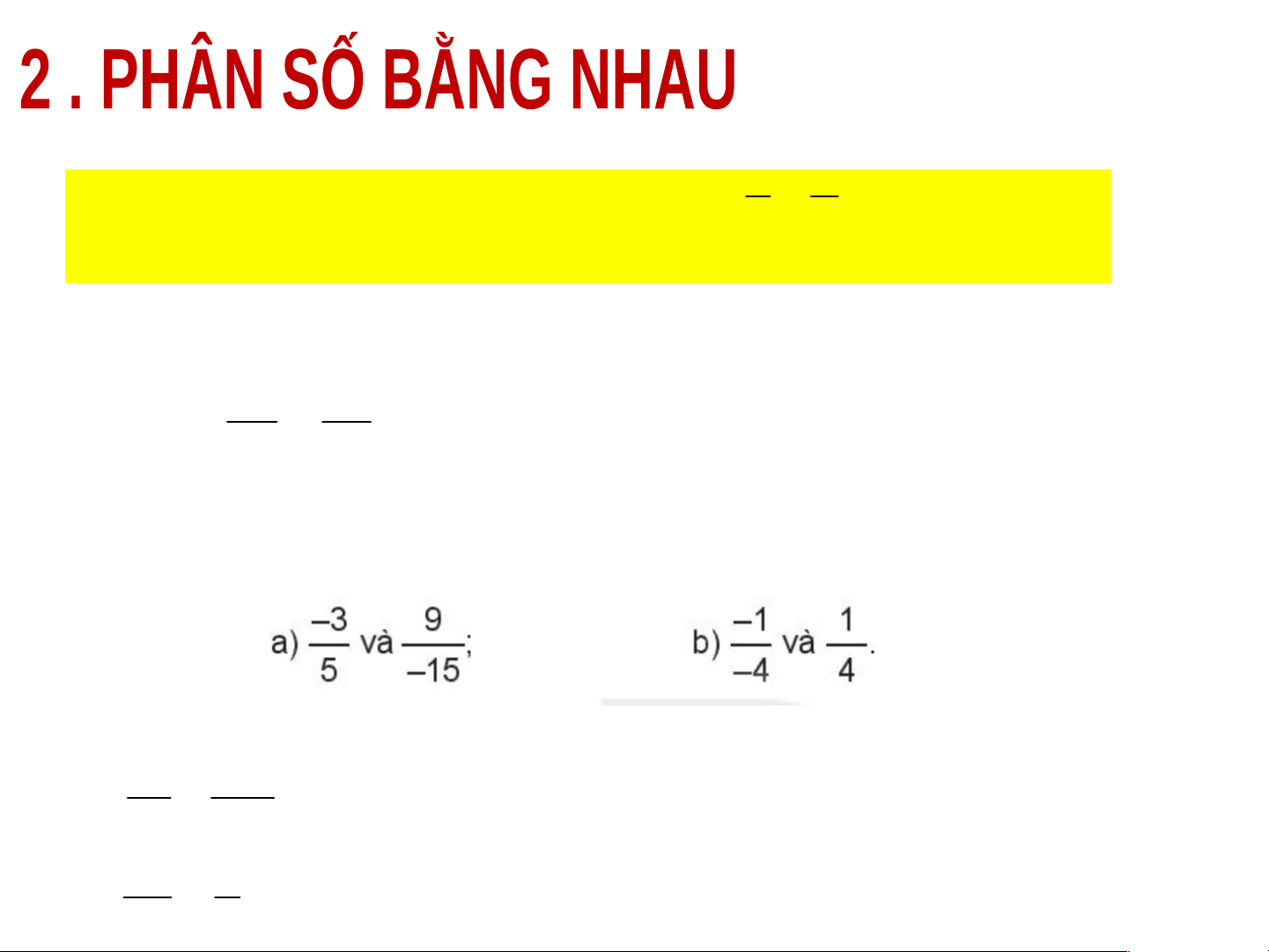
Các cặp phân số sau đây có bằng nhau không? Trả lời  3 9 a) 
Vì (-3) . (-15) = 5 . 9 (cùng bằng 45) 5  15  1 1 b) 
Vì (-1) . 4 = (-4) . 1 (cùng bằng 4)  4 4
Ví dụ : Tìm số nguyên x, biết: x 21  Giải: 4 28 x 21 Vì  nên x . 28 = 4.21 4 28 4.21  x  3  28 Vậy x = 3 Ghi nhớ a 1. Với a,b 
Z, b ≠ 0, ta gọi là một phân số. Trong đó b
a là tử số (tử), b là mẫu số (mẫu) của phân số a c
2. Quy tắc bằng nhau của hai phân số nế  u a.d = b.c b d
- Học thuộc khái niệm phân số và định nghĩa hai phân số bằng nhau.
- Luyện tập cách kiểm tra phân số và hai phân số bằng nhau.
- Luyện tập bài tìm số chưa biết.
- Làm bài tập 6.1; 6.2. 6.3 SGK – Tr 8
BT1 Cho 3 ví dụ về phân số. Cho biết tử và mẫu của mỗi phân số đó.
BT2 Trong các cách viết sau đây, cách viết nào cho ta phân số  2 4 0, 25 6, 23 3 a/ b/ c/ d/ e/ 7 7, 4  3 5 0
BT3 Mọi số nguyên có thể viết dưới dạng phân số không? Cho ví dụ.
Nhận xét: số nguyên a có thể viết
BT3 Mọi số nguyên đều viết được dưới dạng phân số.  2  5 B -2 43 1 - 21 0 ? T 1 2 a., c , . ,  2,  , …
, - l5à những phân số. 3 - 7 5 4 -2 -3 5 1 1 a a   3 1 Chẳng hạn như  3  1 Kết quả: Kết quả: Ví Dụ 2 2 2.( 3)  6    12 ( 12) : 4  3  5 ( 5).( 3) 15   16 16 : 4 4
Chú ý: Mọi phân số đều có thể viết dưới dạng phân số có mẫu dương
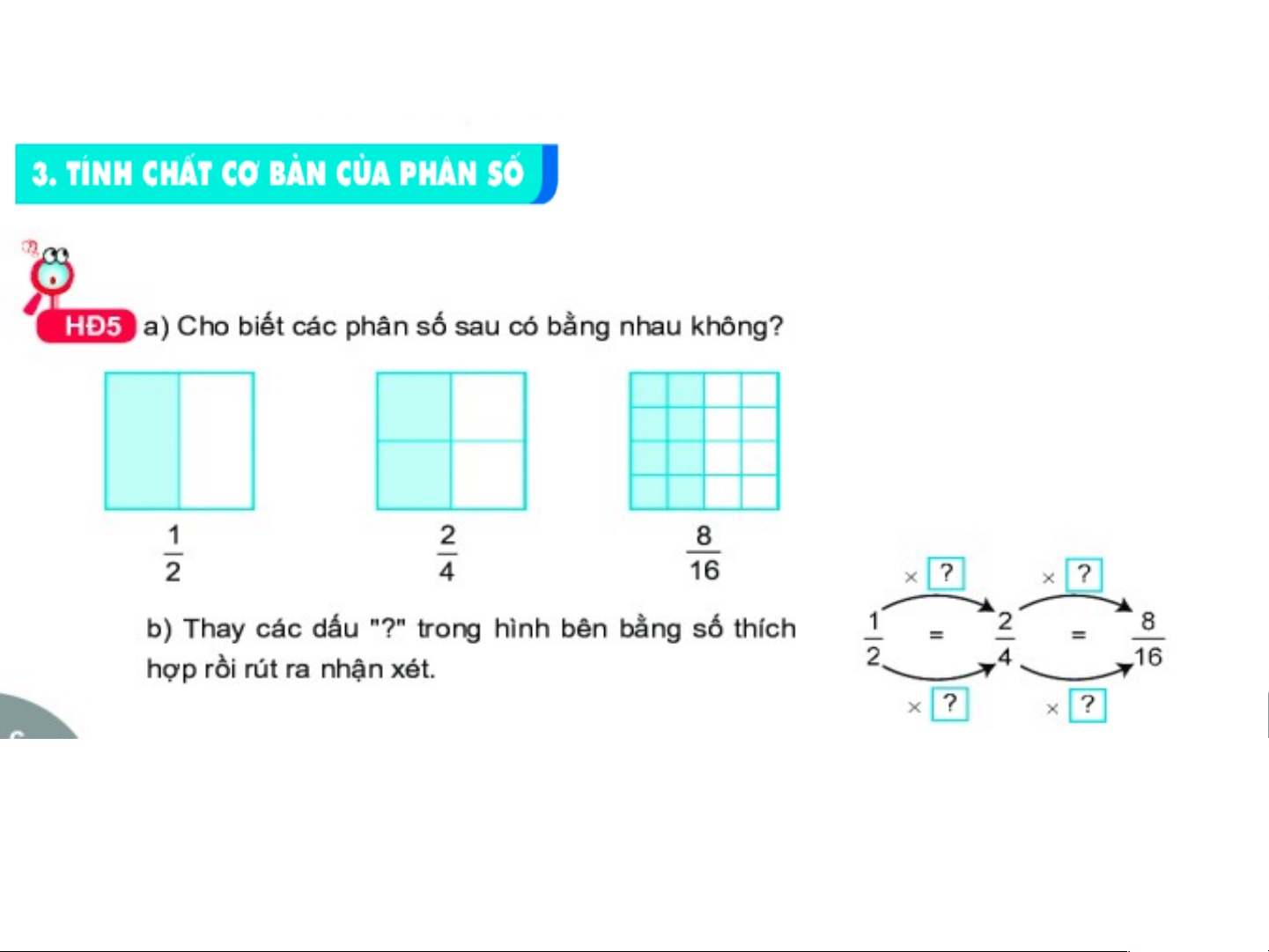
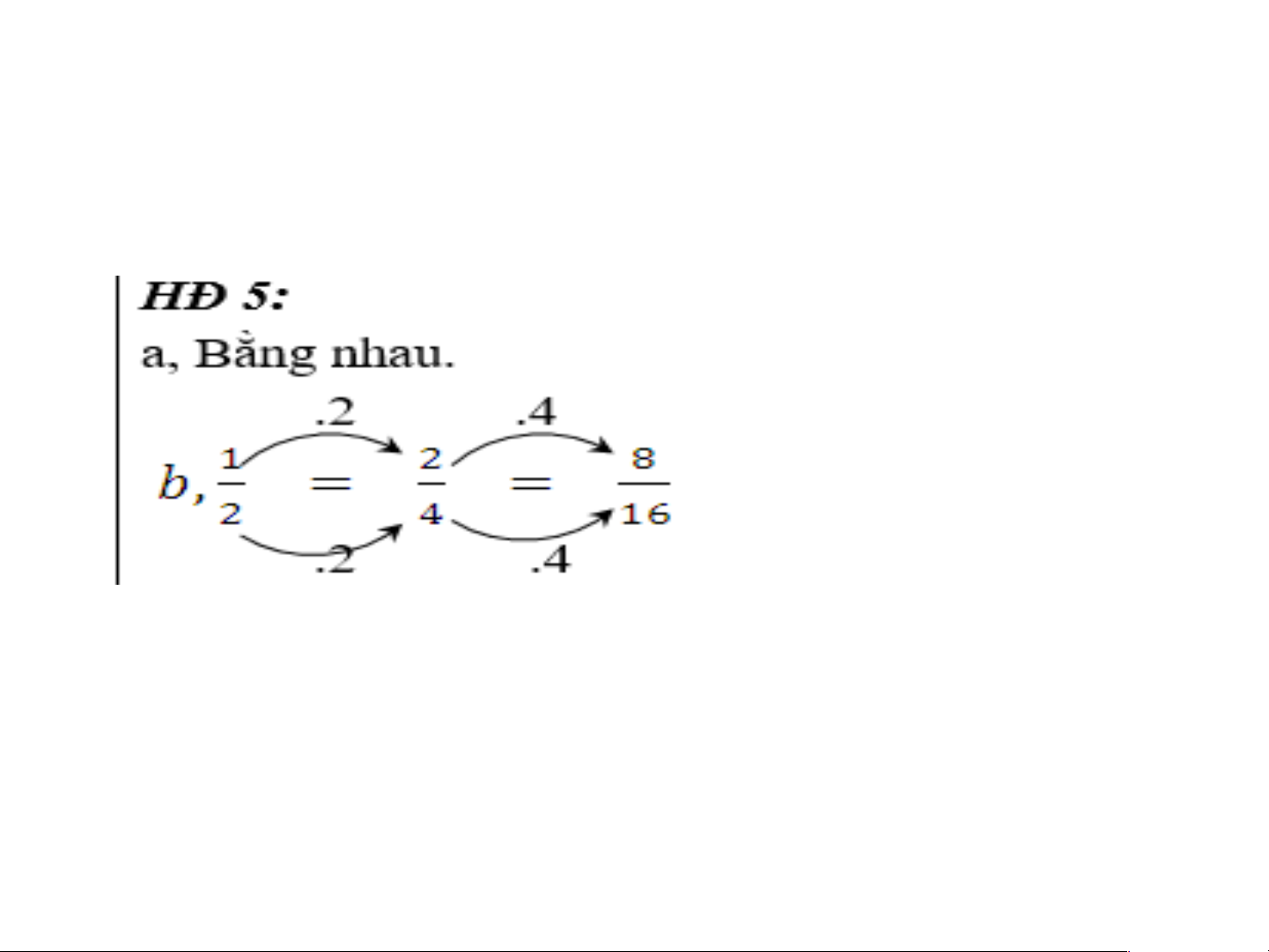
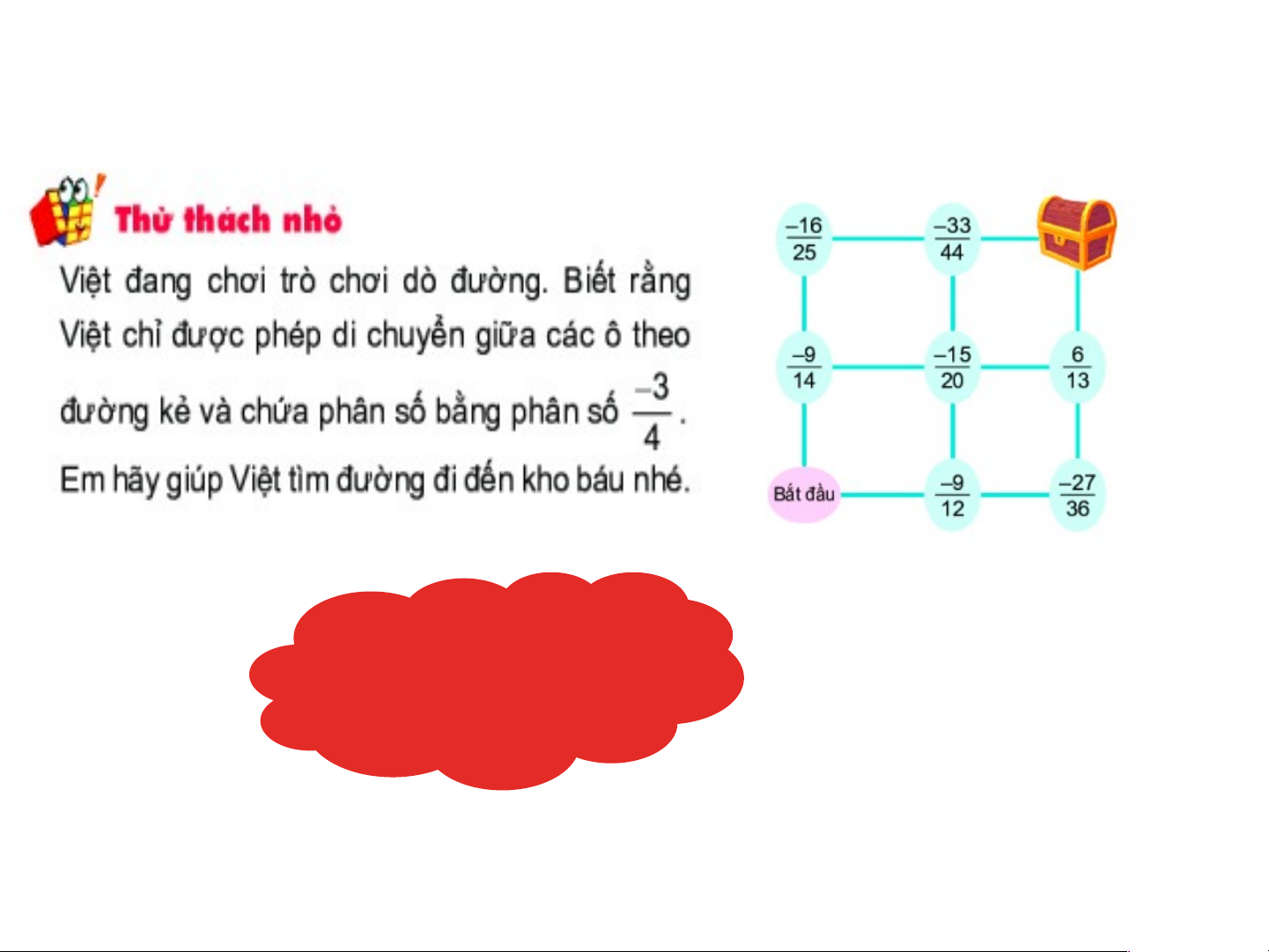
- Người ta thường dùng tính chất 2 để rút gọn phân số. Kết quả: Có nhiều cách đi,
Việt có thể đi như sau: . Kết quả: 0 1 2 3 4 5 6 7 8 9 10 m e Câu 1: Hai phân số n và h bằng nhau nếu …… ……… m.h = n.e ……. 0 1 2 3 4 5 6 7 8 9 10 x  12 Câu 2: Nếu thì x bằng:  4 6 Đáp số: x.6 = - 12. (- 4) x.6 = 48 x = 48 : 6 x = 8
Câu 3: Cặp số bằng nhau là : 0 1 2 3 4 5 6 7 8 9 10  6  5  3 9 a) à v b) à v 5 6 4 12 2 20 2 2 c) à v d ) à v  3  30 3 3 ĐÁP ÁN : Câu c
Câu 4: Nếu x là số nguyên âm 0 1 2 3 4 5 6 7 8 9 10 và : x 5 thì x =….  5 x A / 10 B / -5 C / -25 D / 25 ĐÁP ÁN: Câu B
Bài 6 a. Tìm số nguyên x, biết x 6 7 = 21 Giải Vì x 6  nên x . 21 = 7 . (6) 7 21 7.(6) 42 Suy ra x   2  21 21
b. Tìm số nguyên y, biết: -5 20 y = 28 Giải: -5 20 Vì nên -5 . 28 = y . 20 y = 28 hay y . 20 = -5 . 28  5.28 Suy ra y =  7 20
Kết quả: Số phần tiền thưởng Hà Linh đã tiêu là:
BT1 Cho 3 ví dụ về phân số. Cho biết tử và mẫu của mỗi phân số đó.
BT2 Trong các cách viết sau đây, cách viết nào cho ta phân số  2 4 0, 25 6, 23 3 a/ b/ c/ d/ e/ 7 7, 4  3 5 0
BT3 Mọi số nguyên có thể viết dưới dạng phân số không? Cho ví dụ.
Nhận xét: số nguyên a có thể viết
BT3 Mọi số nguyên đều viết được dưới dạng phân số.  2  5 B -2 43 1 - 21 0 ? T 1 2 a., c , . ,  2,  , …
, - l5à những phân số. 3 - 7 5 4 -2 -3 5 1 1 a a   3 1 Chẳng hạn như  3  1
- Học thuộc khái niệm phân số và định nghĩa hai phân số bằng nhau.
- Luyện tập cách kiểm tra phân số và hai phân số bằng nhau.
- Luyện tập bài tìm số chưa biết.
- Làm bài tập 5; 7; 8; 9; 10/SGK – Tr6,8,9
và Bài 6, 7, 8, 14, 15, 16, 17/SBT – Tr6,7
Document Outline

  • Slide 1
  • Slide 2
  • Slide 3
  • Slide 4
  • Slide 5
  • Slide 6
  • Slide 7
  • Slide 8
  • Slide 9
  • Slide 10
  • Slide 11
  • Slide 12
  • Slide 13
  • Slide 14
  • Slide 15
  • Slide 16
  • Slide 17
  • Slide 18
  • Slide 19
  • Slide 20
  • Slide 21
  • Slide 22
  • Slide 23
  • Slide 24
  • Slide 25
  • Slide 26
  • Slide 27
  • Slide 28
  • Slide 29
  • Slide 30
  • Slide 31
  • Slide 32