Giáo án điện tử Toán 6 Bài 6 Cánh diều: Thứ tự thực hiện các phép tính
Bài giảng PowerPoint Toán 6 Bài 6 Cánh diều: Thứ tự thực hiện các phép tính hay nhất, với thiết kế hiện đại, dễ dàng chỉnh sửa giúp Giáo viên có thêm tài liệu tham khảo để soạn Giáo án Toán 6. Mời bạn đọc đón xem!
Chủ đề: Bài giảng điện tử Toán 6
Môn: Toán 6
Sách: Cánh diều
Thông tin:
Tác giả:
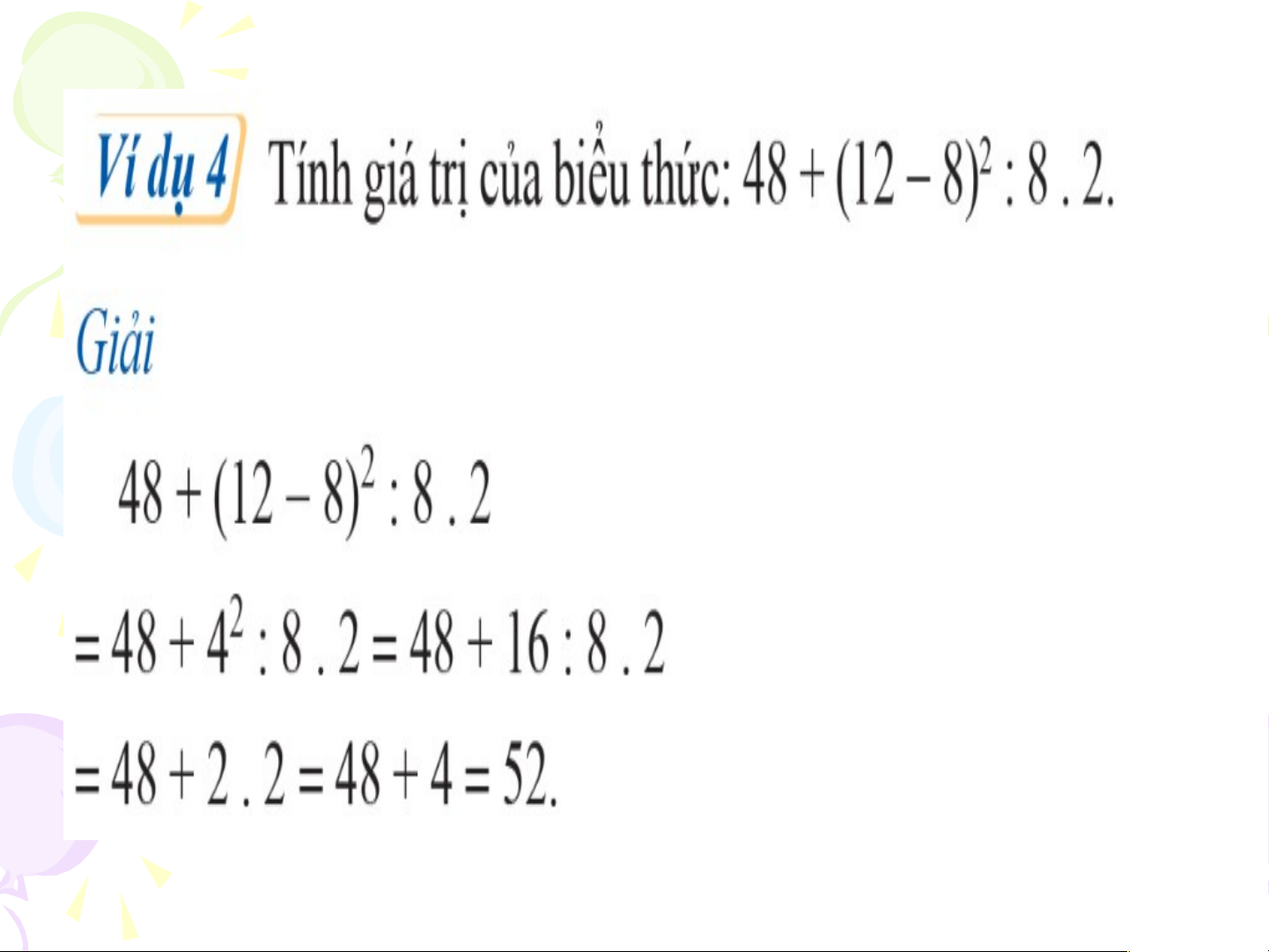
Preview text:
§ 6: THỨ TỰ THỰC HIỆN CÁC PHÉP TÍNH
I. Thứ tự thực hiện các phép tính trong biểu
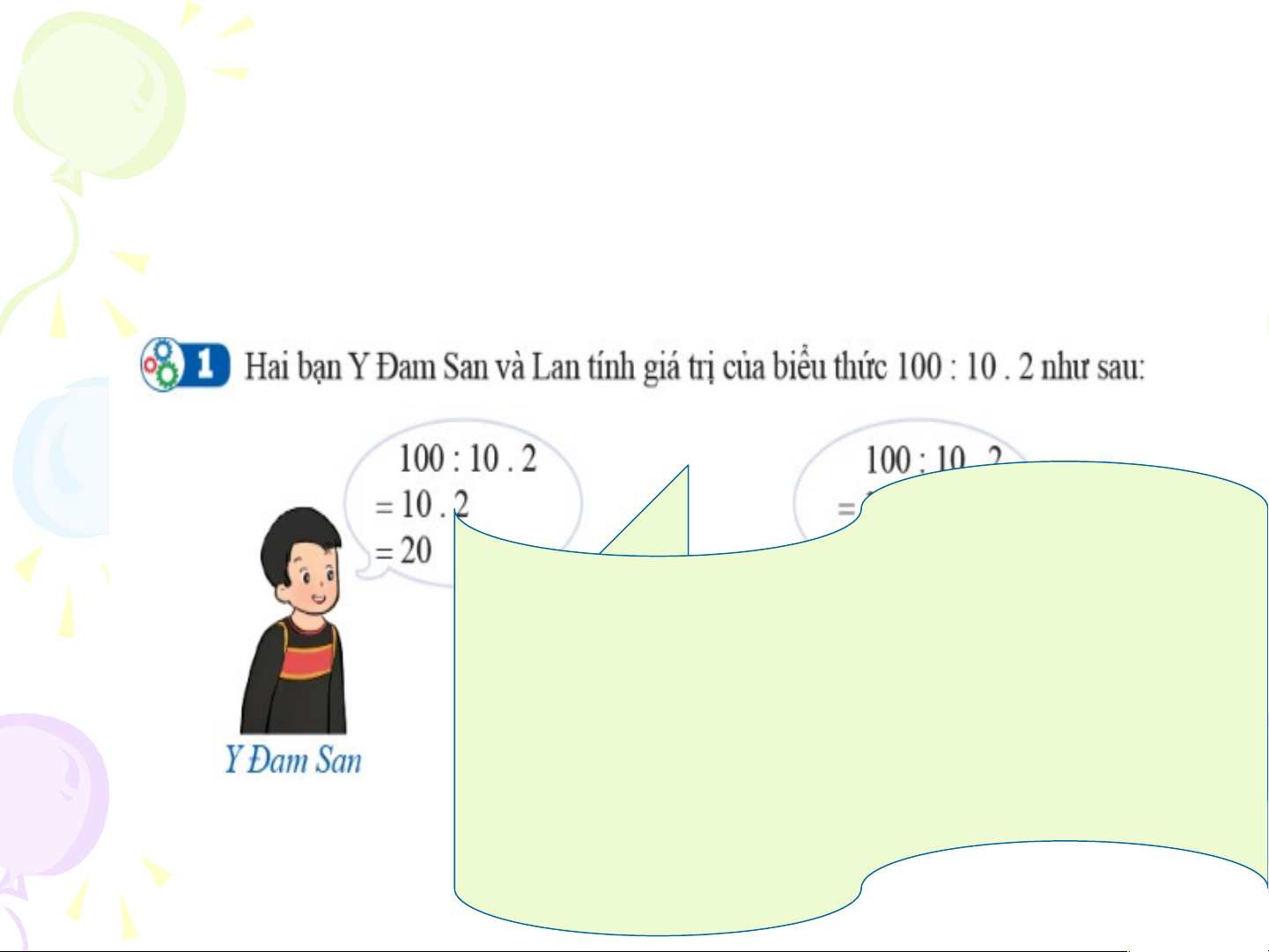
thức không chứa dấu ngoặc • Hoạt động 1: Kết l Bạ
uận n: Y Đam San làm đúng:
Khi biểu thức chỉ có các phép tính cộng 100 : 10 . 2 = 10 . 2 =
và trừ ( hoặc chỉ có các phé 2 p t 0. ính nhân
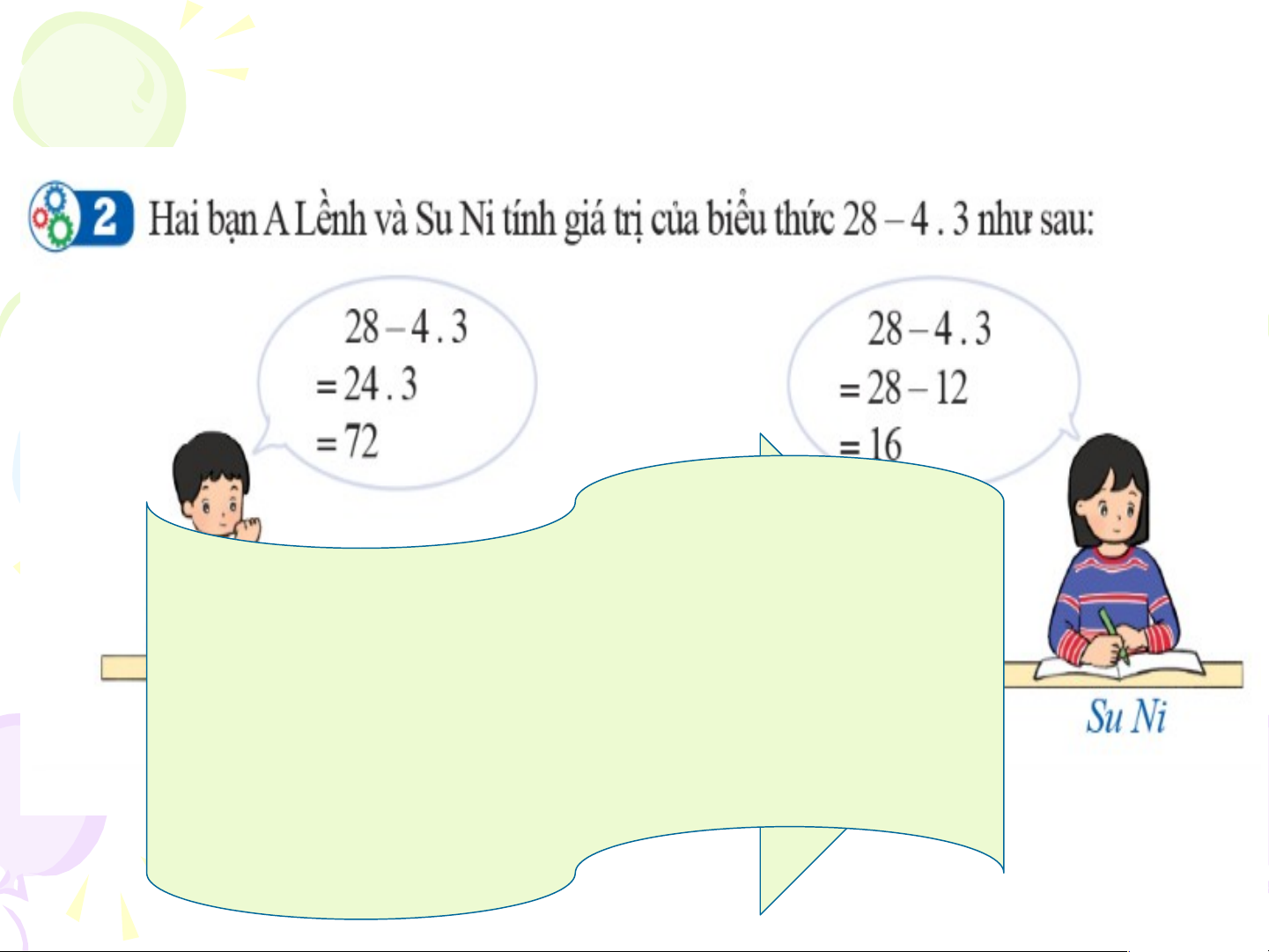
và chia), ta thực hiện phép tính theo thứ tự từ trái sang phải. Luyện tập 1: • a) 507 - 159 - 59 • = 348 - 59 = 289 • b) 180 : 6 : 3 • = 30 : 3 = 10 • Hoạt động 2: K B ếtạ n Su luận N : i làm đúng: K 28 hi – 4.3 = biểu 28 thức – c 1 ó 2 = cá 16 c [hép tính cộng,
trừ, nhân, chia, ta thực hiện phép
tính nhân và chia trước, rồi đến cộng và trừ. Luyện tập 2: • 18 - 4 . 3 : 6 + 12 = 18 - 12 : 6 + 12 = 18 - 2 + 12 = 16 + 12 = 28 • Hoạt động 3: Kết luận:
Khi biểu thức có các phép tính
cộng, trừ, nhân, chia, nâng lên lũy Bạn Phương làm đúng:
thừa, ta thực hiện phép tính nâng 5 + 2. 32
lên lũy thừa trước, rồi đến nhân và = 5 + 2.9 = chi 5 + a, c 18 = 23.
uối cùng đến cộng và trừ. Luyện tập 3: • 43 : 8. 32 - 52 + 9 = 64 : 8.9 – 25 + 9 = 8.9 – 25 + 9 = 72 – 25 + 9 = 47 + 9 = 56
II. Thứ tự thực hiện các phép tính trong
biểu thức chứa dấu ngoặc. • Hoạt động 4: Kết Bạn luận: A Lềnh làm đúng: Khi bi( 30 + 5) : 5 ểu thức có chứa dấu ngoặ = 35 : 5 = 7
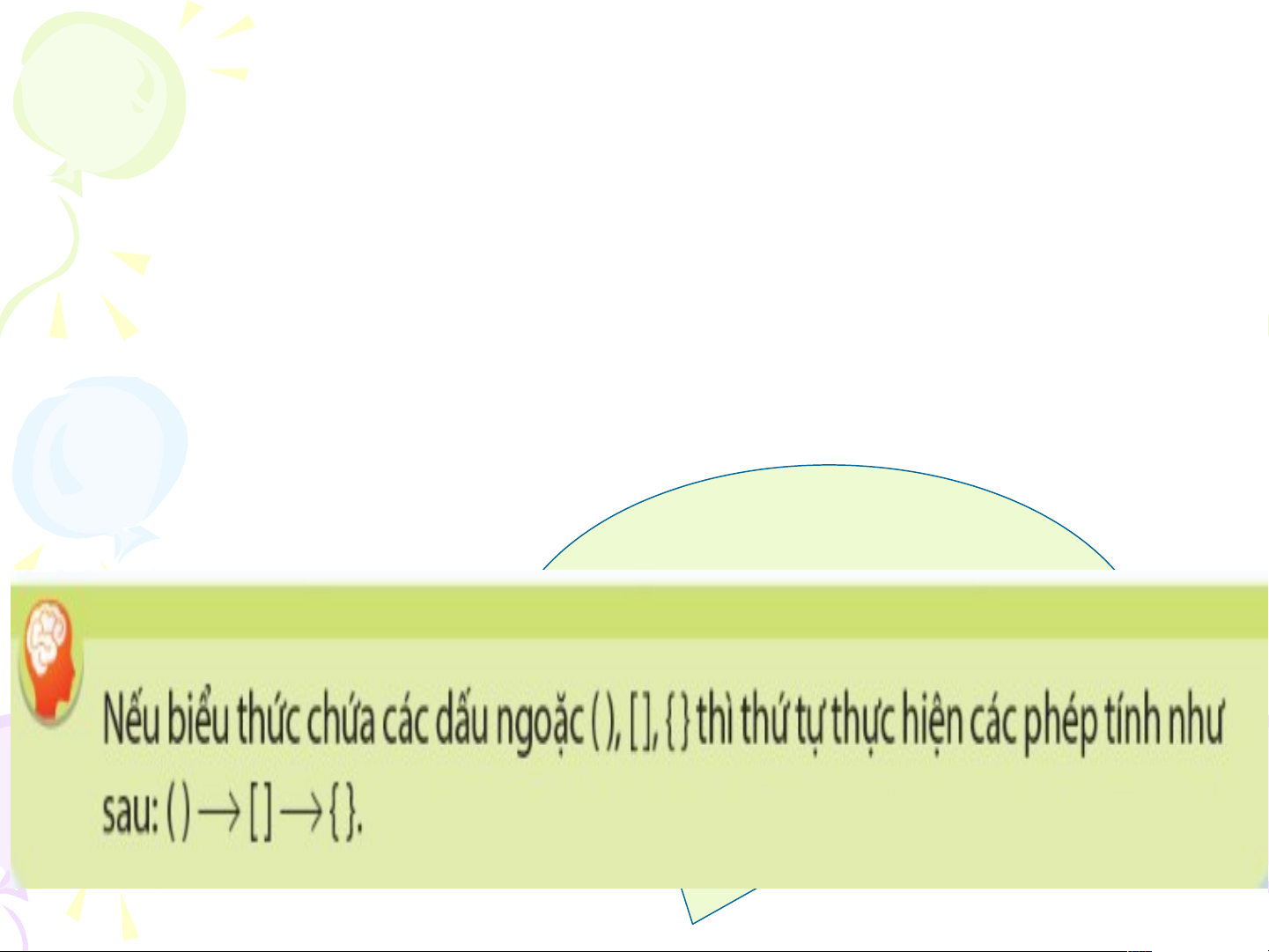
c, ta thực hiện các phép tính trong dấu ngoặc trước. Luyện tập 4: • 15 + (39 : 3 - 8) . 4 = 15 + (13 - 8) . 4 = 15 + 5 . 4 = 15 + 20 = 35. • Hoạt động 5: • 180 : {9+3.[30 – (5-2)]} = 180 : {9 + 3.[30-3]} = 180 : { 9 + 81} = 180 : 90 = 2 Quan sát các bước làm và nhận xét thự tự thực hiện phép tính Luyện tập 5:
• 35 - {5 . [(16 + 12) : 4 + 3] - 2 . 10}
= 35 - {5 . [28 : 4 + 3] - 20} = 35 - {5 . [7 + 3] - 20} = 35 - {5 . 10 - 20} = 35 - {50 - 20} = 35 - 30 = 5 Bài Tập 1 • Thực hiện phép tính: a) 2 370 - 179 + 21 = 2 191 + 21 = 2 212 b) 100 : 5 . 4 =20 . 4 = 8 c)396 : 18 : 2 =22:2 =11 Bài Tập 2 • Thực hiện phép tính: a) 143 - 12 . 5 = 143 - 60 = 83 b) 27 . 8 - 6 : 3 = 216 - 2 = 214 c) 36 - 12 : 4 . 3 + 17 = 36 - 3 . 3 + 17 = 36 - 9 + 17 = 27 + 17 = 44 Bài Tập 3 • Thực hiện phép tính: a) 32.53 + 92
= 9.125 + 81 = 1 125 + 81 =1 206 b) 83 : 42 - 52 = 512 : 16 - 25 =32 - 25= 7 c) 33.92 – 52.9 + 18 : 6 = 27.81 – 25.9 + 3 = 2 187 – 225 + 3 = 1 962 + 3 = 1 965 Bài Tập 4 • Thực hiện phép tính: a) 32 – 6.( 8 – 23) + 18 = 32 – 6.(8-8) + 18 = 32 – 6.0 + 18 =32 + 18 = 50
b) (3.5 – 9)3 . (1 + 2 . 3)2 + 42
= (15 – 9)3 . ( 1 + 6)2 + 42
= 63 . 72 + 42 = 216 . 49 + 16 = 10 584 + 16 =10 600. Bài Tập 5 • Thực hiện phép tính: a) 9 234 : [3.3 .(1+ 83)] =9 234 : [3 . 3 . (1 + 512)]
= 9 234 : [3 . 3 . 513] = 9 234 : 4617 = 2
b) 76 – { 2. [2.52 – ( 31- 2.3)]} + 3.25
= 76 - {2 . [2 . 25 - (31 - 6)]} + 75 = 76 - {2 . [50 - 25]} + 75 = 76 - {2 . 25} + 75 = 76 - 50 + 75 = 101
Hướng dẫn học tập ở nhà.
- Ghi nhớ các kiến thức của bài
-Làm các bài tập 6,7,8, 9 trong SGK
-Đọc trước bài mới “Bài 7:Quan hệ
chia hết, tính chất chia hết” cho tiết học sau.
Document Outline
- Slide 1
- Slide 2
- § 6: THỨ TỰ THỰC HIỆN CÁC PHÉP TÍNH
- Slide 4
- Slide 5
- Luyện tập 1:
- Slide 7
- Slide 8
- Luyện tập 2:
- Slide 10
- Slide 11
- Luyện tập 3:
- Slide 13
- Slide 14
- Luyện tập 4:
- Slide 16
- Slide 17
- Luyện tập 5:
- Bài Tập 1
- Bài Tập 2
- Bài Tập 3
- Bài Tập 4
- Bài Tập 5
- Slide 24
- Slide 25