Giáo án điện tử Toán 6 Bài 7 Cánh diều: Đối xứng trong thực tiễn (tiết 1)
Bài giảng PowerPoint Toán 6 Bài 7 Cánh diều: Đối xứng trong thực tiễn (tiết 1) hay nhất, với thiết kế hiện đại, dễ dàng chỉnh sửa giúp Giáo viên có thêm tài liệu tham khảo để soạn Giáo án Toán 6. Mời bạn đọc đón xem!
Chủ đề: Bài giảng điện tử Toán 6
Môn: Toán 6
Sách: Cánh diều
Thông tin:
Tác giả:
Preview text:
GV DẠY: AI NHANH HƠN H O Ạ T Đ Hình nào Ộ
Hình nào có tâm đối có trục đối N G xứng? xứng? K H Ở I ĐỘNG Ai nhanh hơn *Luật chơi: H O
+) Hoạt động nhóm, mỗi nhóm một đội từ 2 đến 3 học sinh Ạ T
+) Nhiệm vụ của mỗi đội chơi là quan sát các hình 1; 2; 3 để Đ Ộ
tìm ra hình có tính đối xứng. N G
+) Thời gian hoạt động nhóm: 30 giây K H *Cách tính điểm: Ở I
+) Mỗi hình đúng được 2 điểm. Đ Ộ
+) Hoàn thành trước hoặc đúng thời gian quy định: 10 điểm N G
Đội nào có số điểm cao điểm hơn, đội đó chiến thắng.
Hình nào có trục đối xứng? H
Hình nào có tâm đối xứng? O Ạ T Đ Ộ N G KHỞI Hình 1 Hình 2 Hình 3 Đ Ộ N G
Hình có trục đối xứng Hình 2 Hình 3
Hình có tâm đối xứng Hình 1 Hình 3 GV DẠY: H HOẠT ĐỘNG NHÓM: O Ạ T
+) Mỗi nhóm tối đa 5 HS. Đ Ộ
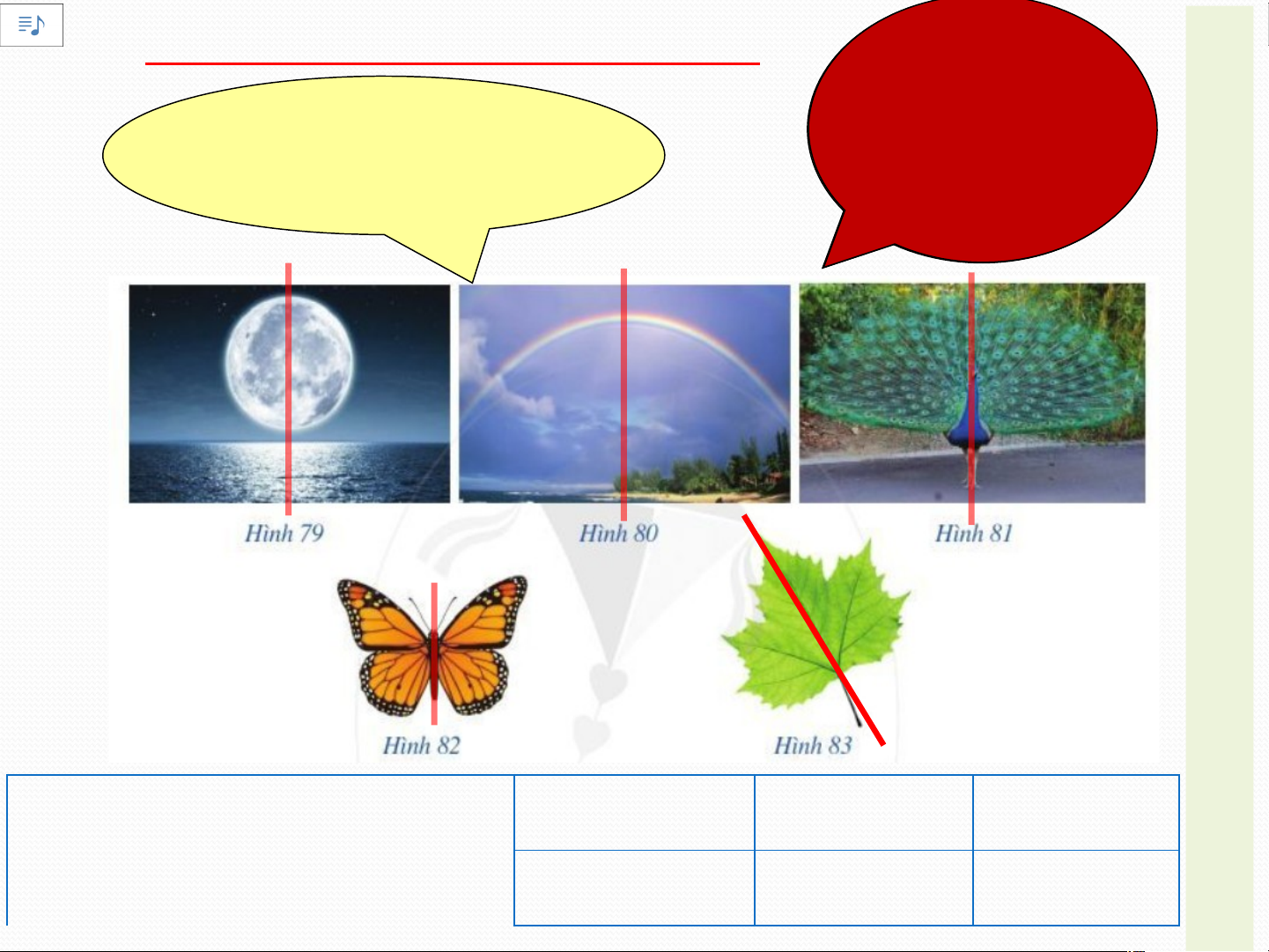
+) Nhiệm vụ: quan sát các hình 79, 80, 81, 82, 83(SGK) để tìm N
ra hình có trục đối xứng hoặc tâm đối xứng. Thảo luận, G
thống nhất và dùng bút chì đánh dấu tâm đối xứng của mỗi H
hình tìm được trong SGK. ÌNH +) Thời gian: 1 phút T H *Cách tính điểm: À N
+) Xác định đúng tính đối xứng của mỗi hình: 1 điểm, tìm được H
tâm hoặc trục đối xứng của mỗi hình: 1 điểm K IẾ
+) Hoàn thành trước hoặc đúng thời gian quy định: 10 điểm N T
Nhóm nào điểm cao được cộng điểm thưởng. H Ứ C H
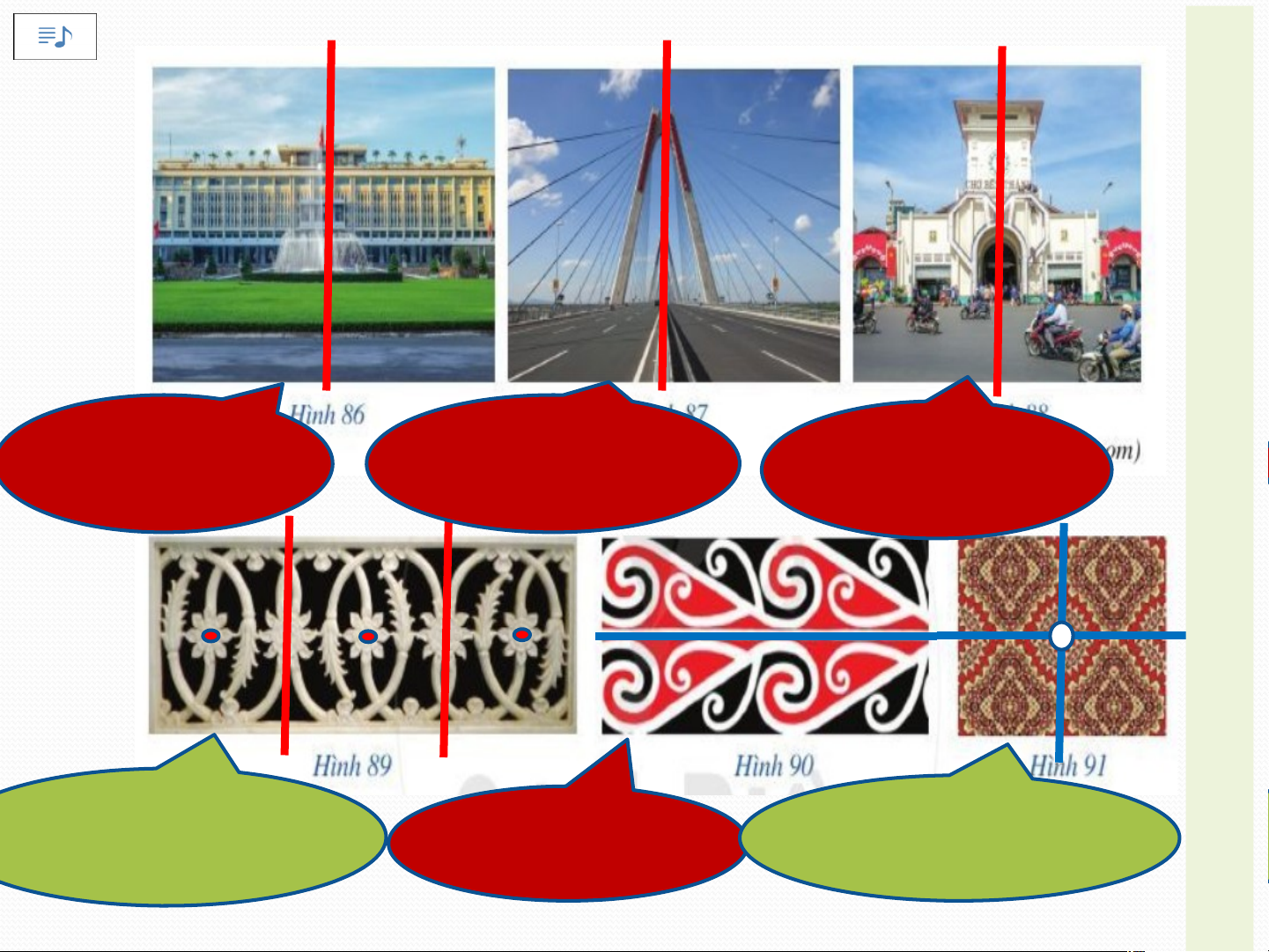
1.Tính đối xứng trong thế giới tự nhiên: Hìn K h h n ô à n o g O Ạ Hình nào có trục có h ìtâ n m h nđ àố o i T đối xứng? c x ó ứn tâ g m ? đối Đ xứng Ộ N G H ÌNH THÀNH KIẾN TH Hình 79 Hình 80 Hình 81
Hình có trục đối xứng Ứ C Hình 82 Hình 83 H O
1.Tính đối xứng trong thế giới tự nhiên: Ạ T
- Trong tự nhiên, tính đối xứng được thể hiện rất đa ĐỘ dạng, phong phú. N G H T - ính Tí đố nh đ i ố i xứn xứ g ng ccủa ủa mm ộtỗi đ đ ối ối tư tượn ợng g g có iúp c vai húng t rò ta gì? ÌN (Hoạt đ nhanh ộng chó n
ngh óm c
định ặp đô hình i t đ ro ối n g 3 tư 0 g ợngiâ y đ đ ó ể tìm khi câ nhì u n t v rả à lờ o i ) H nó. T H À N - Tính Tín đố h đi ốxiứ ng t xứn ạo g ra củ sự a c m ân ỗi b hằìng nh (cân giú xứ p í ng), ch hài gì ho ch à, o H
trật tự, quen thuộc và nhờ đó tạo ra thẩm mĩ (vẻ đẹp) K chúng ta? IẾ
(Hoạt động nhóm cặp đôi trong 30 giây để tìm câu trả lời ) N T H Ứ C H
HOẠT ĐỘNG CÁ NHÂN: O Ạ
Hãy xác định tính đối xứng của các hình sau? T Đ Ộ N Hình có trục G đối xứng H ÌNH THÀ Hình có trục N đối xứng H K IẾN THỨC H Hãy xác HOẠ đ T ịnh t ĐỘNG í C nh Á NHđố
ÂN: i xứng của các hình sau? OẠT ĐỘNG HÌNH T Hình có trục Hình có trục Hình có trục H đối xứng đối xứng đối xứng À N H K IẾN THỨ Hình có trục và Hình có trục Hình có trục và C tâm đối xứng đối xứng tâm đối xứng H
HOẠT ĐỘNG CÁ NHÂN: O Ạ
Hãy xác định tính đối xứng của các hình sau? T ĐỘNG HÌNH T Hình có trục H Hình có trục đối xứng À đối xứng N H K IẾN THỨ Hình có trục Hình có trục C đối xứng đối xứng H
HOẠT ĐỘNG NHÓM CẶP ĐÔI: O
Hãy xác định trục(hoặc tâm) đối xứng của Ạ T mỗi hình? Đ Ộ N G Hình có trục H Ì đối xứng N H T H À N H K Hình có trục IẾ đối xứng N T H Ứ C H Hãy HOẠT xác Đ địỘ nNG h NH trụÓM CẶ c(ho P ặ ĐÔI
c tâ:m) đối xứng của mỗi hình O?ẠT ĐỘNG HÌNH Hình có trục Hình có trục Hình có trục T đối xứng đối xứng đối xứng H À N H K IẾN TH Hình có trục và Hình có trục Hình có trục và Ứ tâm đối xứng đối xứng tâm đối xứng C H Hã H y O x ẠT ĐỘNG ác định CtÁ NH rục(ÂN:
hoặc tâm) đối xứng của mỗi hìn Oh? Ạ T Đ Ộ N G HÌNH Hình có trục T Hình có trục đối xứng H đối xứng À N H K IẾN THỨ Hình có trục Hình có trục C đối xứng đối xứng H O
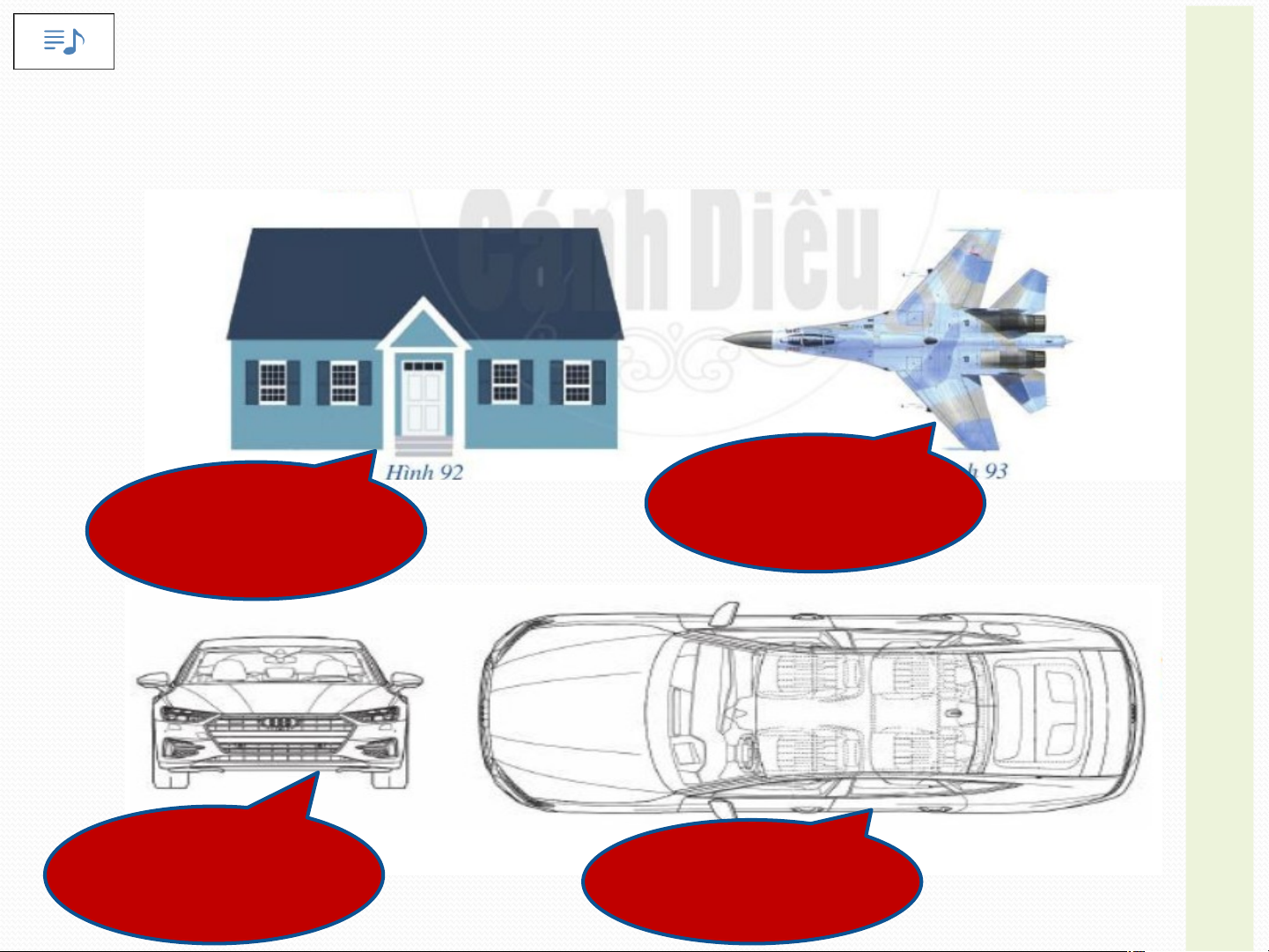
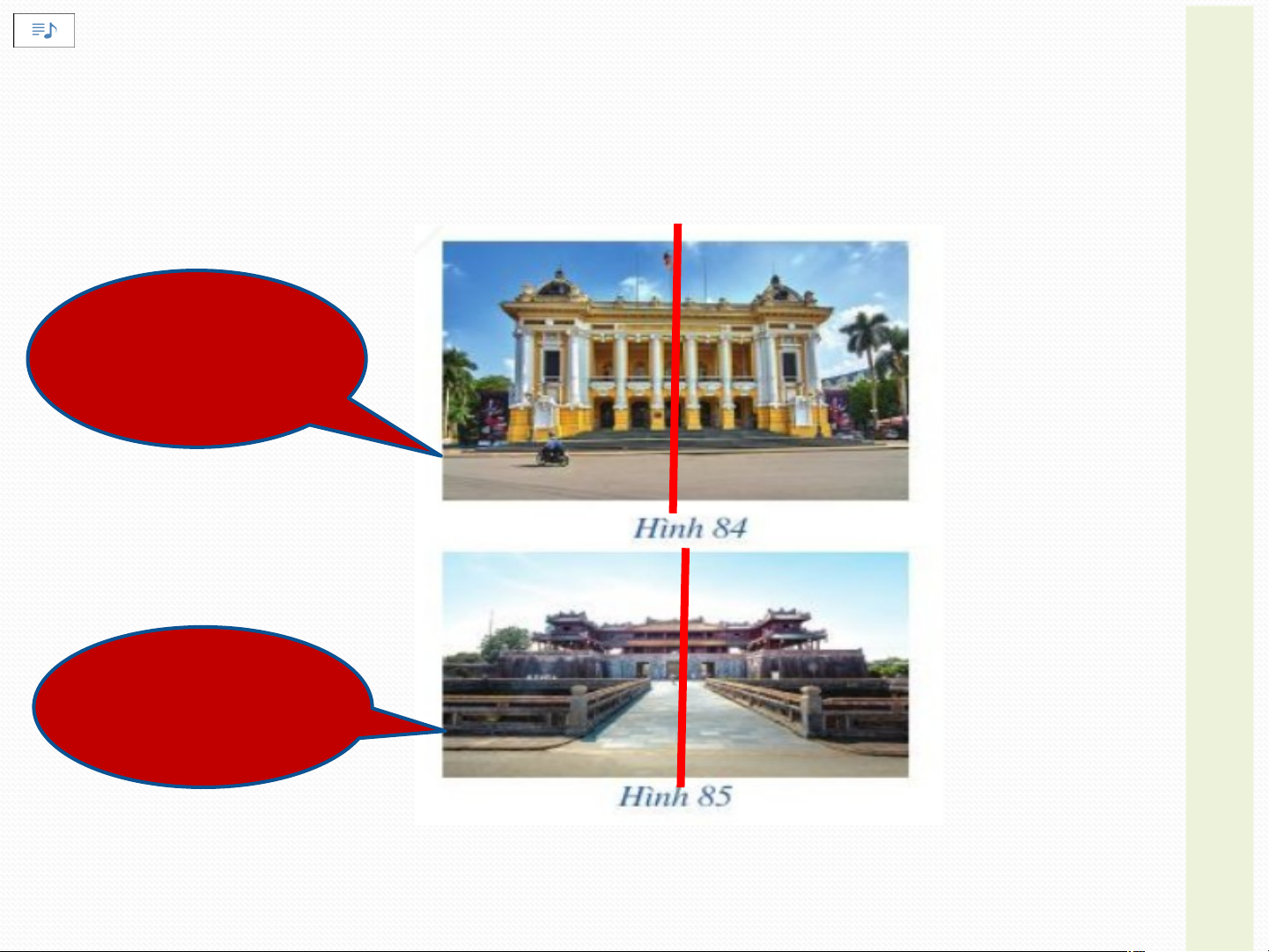
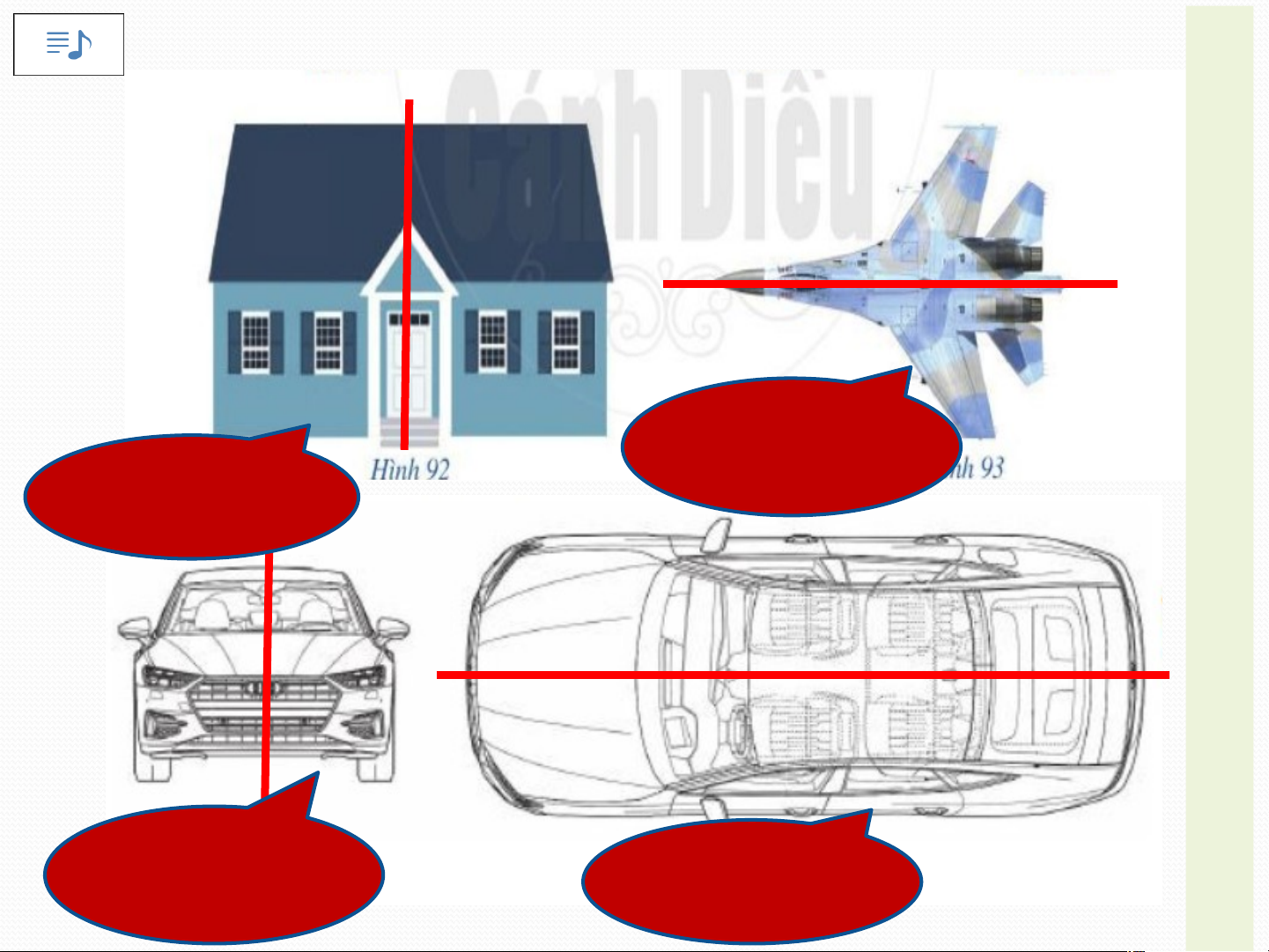
2. Tính đối xứng trong nghệ thuật, kiến trúc và Ạ công nghệ: T Đ Ộ
Hầu hết thiết kế về kiến trúc, đồ họa hay một tác phẩm N
HOẠT ĐỘNG NHÓM CẶP ĐÔI: G
nghệ thuật nào đều phải thực hiện tốt yếu tố cân bằng. Tí V nh ì th đối ế, bốxứ c ng ục đ đư ối x ợ ứ c sử ng th dụng ường đ tr ư ong ợc s c ử ác dụ tác ng tr phẩm ong cá H c ÌN ng t h ác ệ phth ẩ uậ m t n ha ghệ y t ki h ến uật t h rúc ay bở kiến i tyếu rúc. tố nào? H T H À
HOẠT ĐỘNG NHÓM CẶP ĐÔI: N
- Các công trình hay máy móc muốn tồn tại, ổn định, H
Trong thiết kế công nghệ, chế tạo K
bền vững và có được vẻ đẹp, bắt mắt thì phải chú IẾN
tính đối xứng có vai trò gì?
trọng đến tính cân xứng. T H Ứ C
HƯỚNG DẪN HỌC Ở NHÀ: -
Tìm hiểu thêm các hình có tính chất đối xứng
trong thực tiễn (động vật. thực vật, công trình, kiến trúc). -
Làm bài tập : 1, 2(Tr 116-SGK). -
Chuẩn bị dụng cụ: Kéo cắt giấy, giấy màu có
ô vuông, bút chì, thước thẳng để thực hành vào tiết sau.
Chúc các em học tốt bài ở nhà!
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17