





Preview text:
PHẦN BÀI TẬP HÌNH BÌNH HÀNH
(SÁCH GIÁO KHOA 8 – KNTT)
Bài 3.13 trang 61 Toán 8 Tập 1: Trong
các khẳng định sau, khẳng định nào đúng,
khẳng định nào sai? Vì sao?
a) Hình thang có hai cạnh bên song song là hình bình hành.
b) Hình thang có hai cạnh bên bằng nhau là hình bình hành.
c) Tứ giác có hai cạnh đối nào cũng song song là hình bình hành. Lời giải:
a) Hình thang là tứ giác có một cặp cạnh song song.
Suy ra hình thang có hai cạnh
bên song song thì hình này có
hai cặp cạnh đối song song.
Do đó hình thang có hai cạnh
bên song song là hình bình hành.
Vậy khẳng định a) đúng.
Bài 3.13 trang 61 Toán 8 Tập 1: Trong
các khẳng định sau, khẳng định nào đúng,
khẳng định nào sai? Vì sao?
a) Hình thang có hai cạnh bên song song là hình bình hành.
b) Hình thang có hai cạnh bên bằng nhau là hình bình hành.
c) Tứ giác có hai cạnh đối nào cũng song
song là hình bình hành. Lời giải:
b) Hình thang có hai cạnh bên bằng
nhau nhưng không song song nên
không phải là hình bình hành. Vậy khẳng định b) sai.
c) Tứ giác có hai cạnh đối nào cũng
song song hay có hai cặp cạnh đối
song song nên tứ giác đó là hình bình hành.
Vậy khẳng định c) đúng.
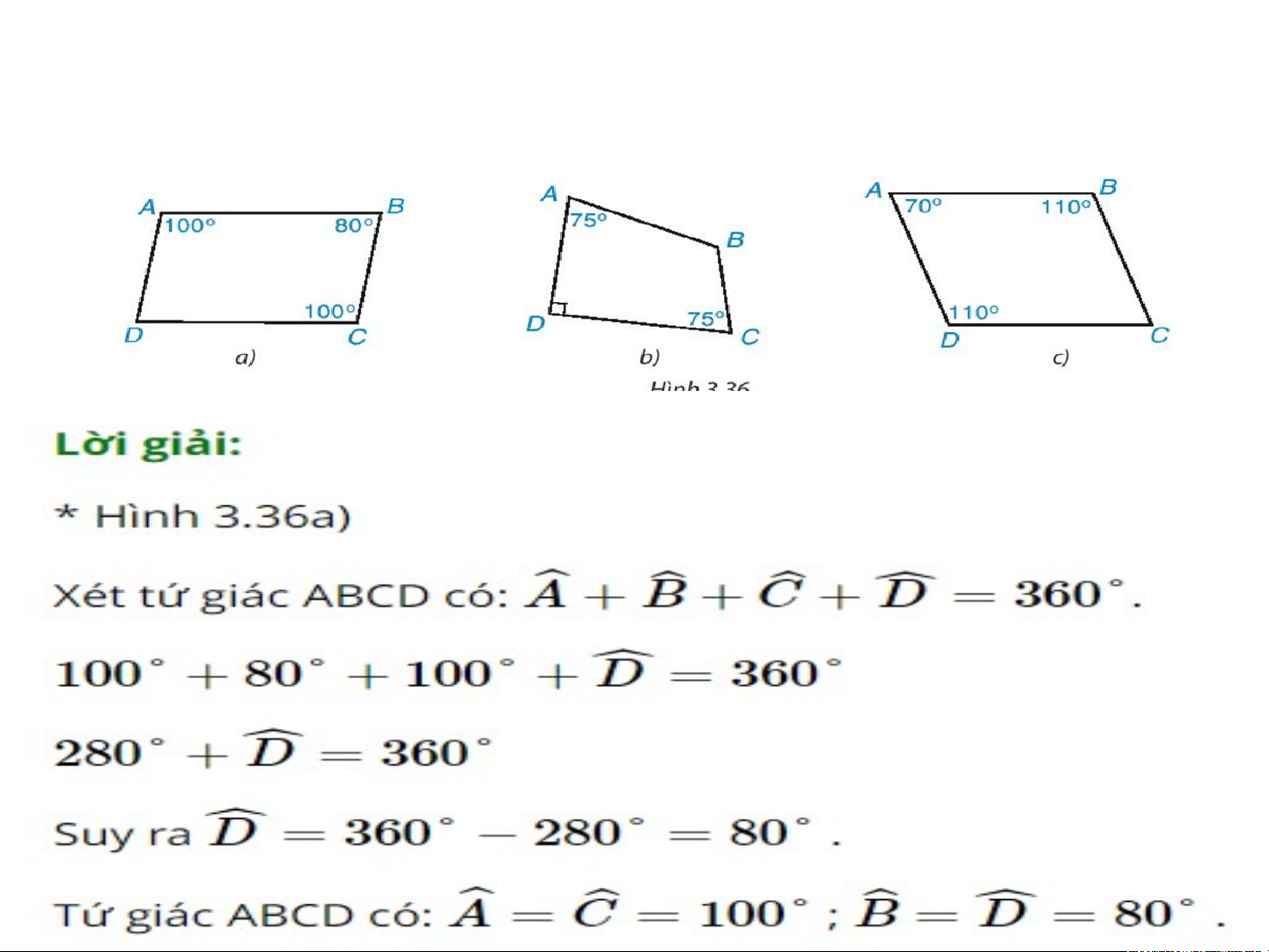
Bài 3.14 trang 61 Toán 8 Tập 1: Tính các góc còn lại
của hình bình hành ABCD trong Hình 3.35.
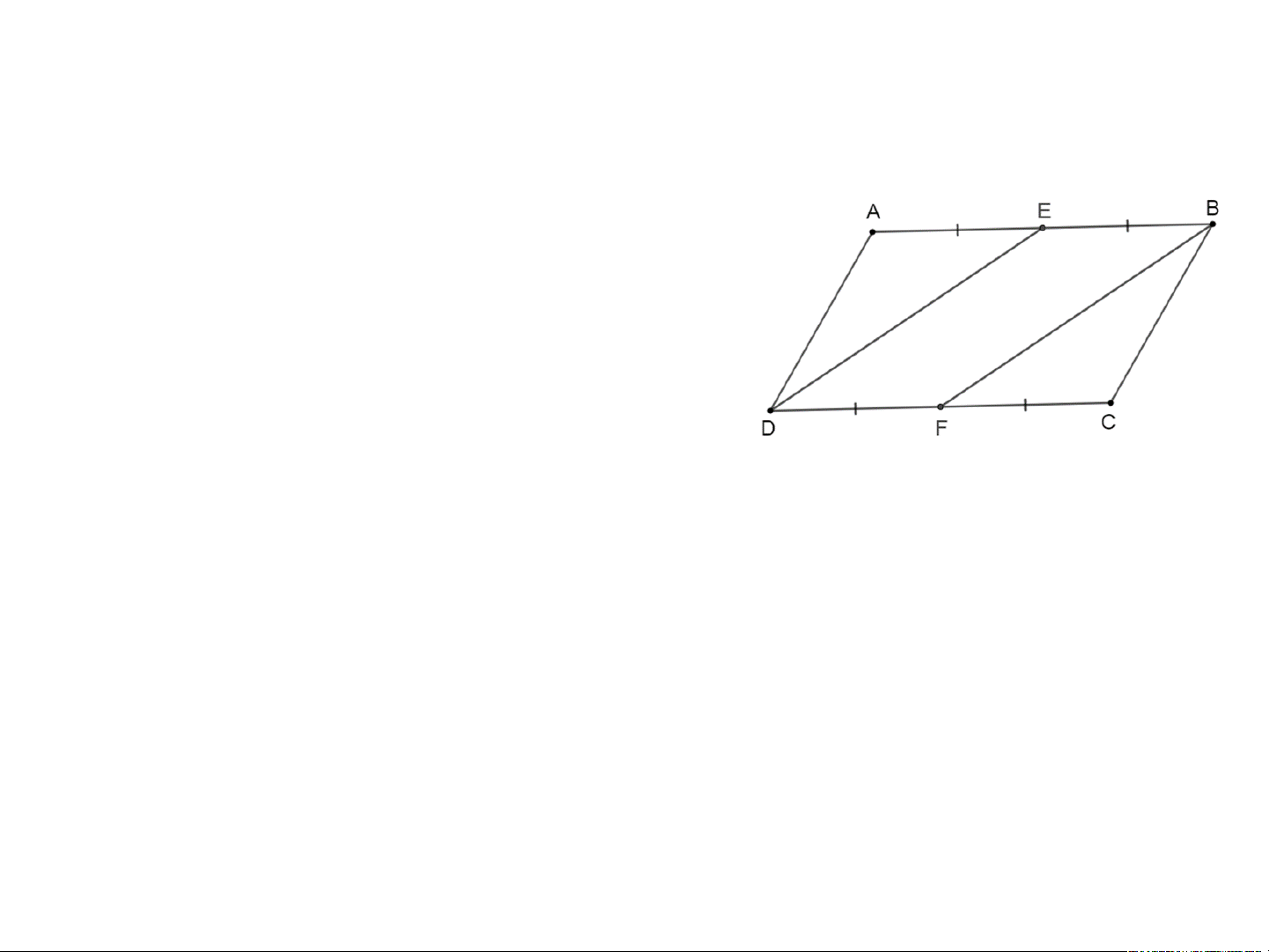
Bài 3.15 trang 61 Toán 8 Tập 1: Cho hình bình hành
ABCD. Gọi E, F lần lượt là trung điểm của AB, CD. Chứng minh BF = DE. Lời giải:
Vì ABCD là hình bình hành nên AB = CD, AB // CD.
Mà E, F lần lượt là trung điểm của AB, CD nên AE = BE = AB, CF = DF = CD. Do đó AE = BE = CF = DF. Xét tứ giác BEDF có: BE = DF (chứng minh trên); BE // DF (vì AB // CD)
Do đó tứ giác BEDF là hình bình hành Suy ra BF = DE (đpcm).
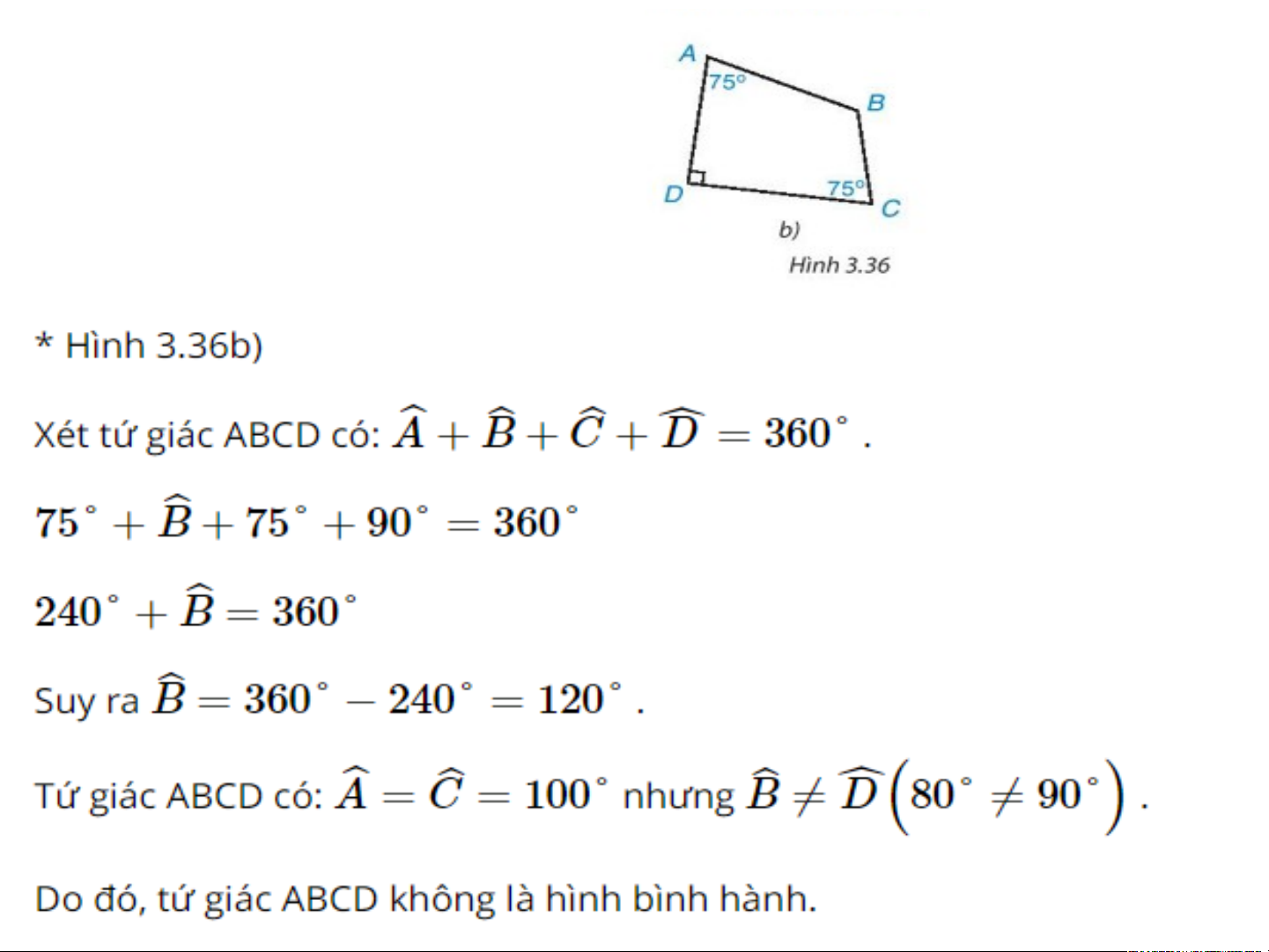
Bài 3.16 trang 61 Toán 8 Tập 1: Trong mỗi trường hợp
sau đây, tứ giác nào là hình bình hành, tứ giác nào không
là hình bình hành? Vì sao?
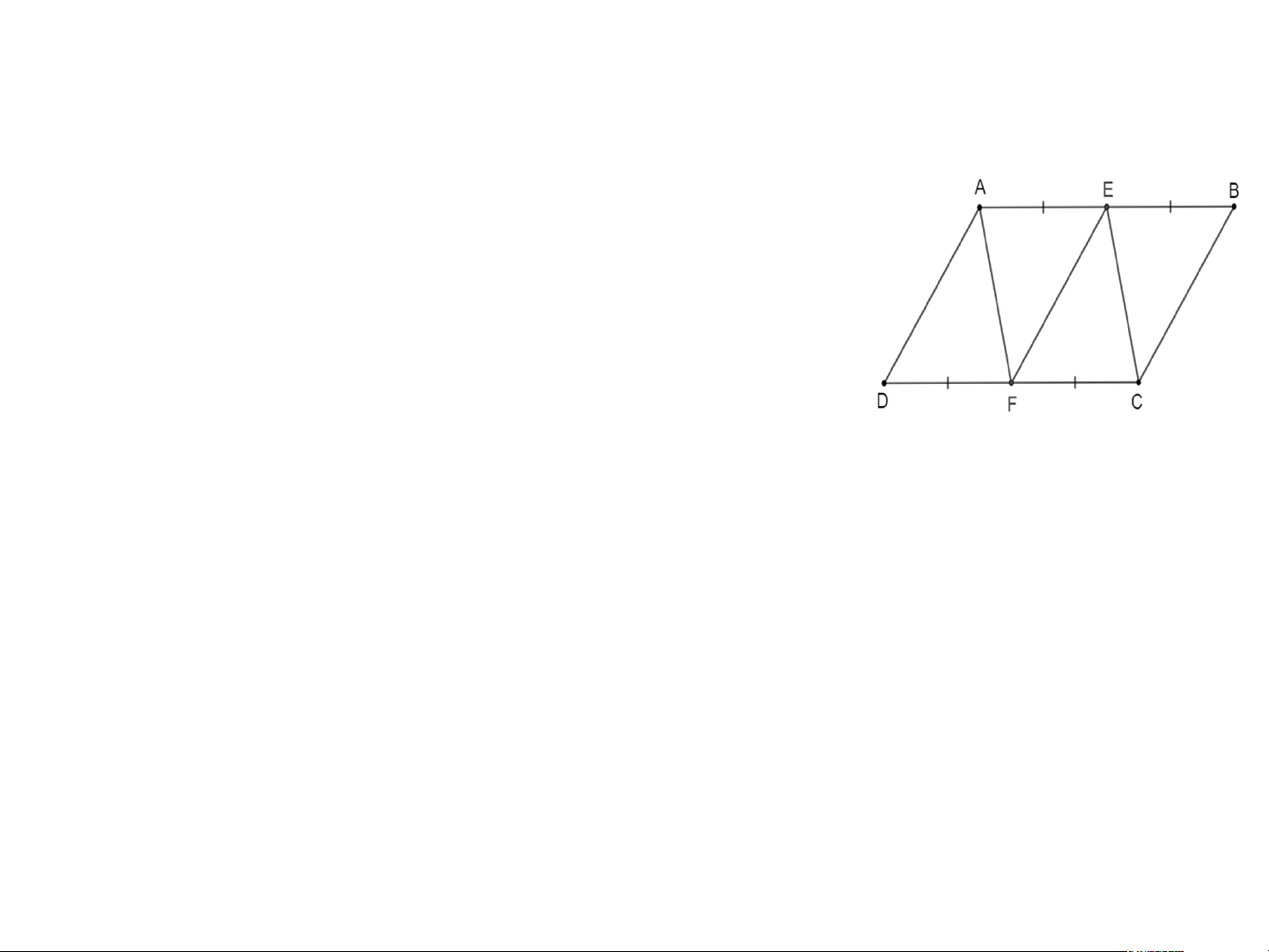
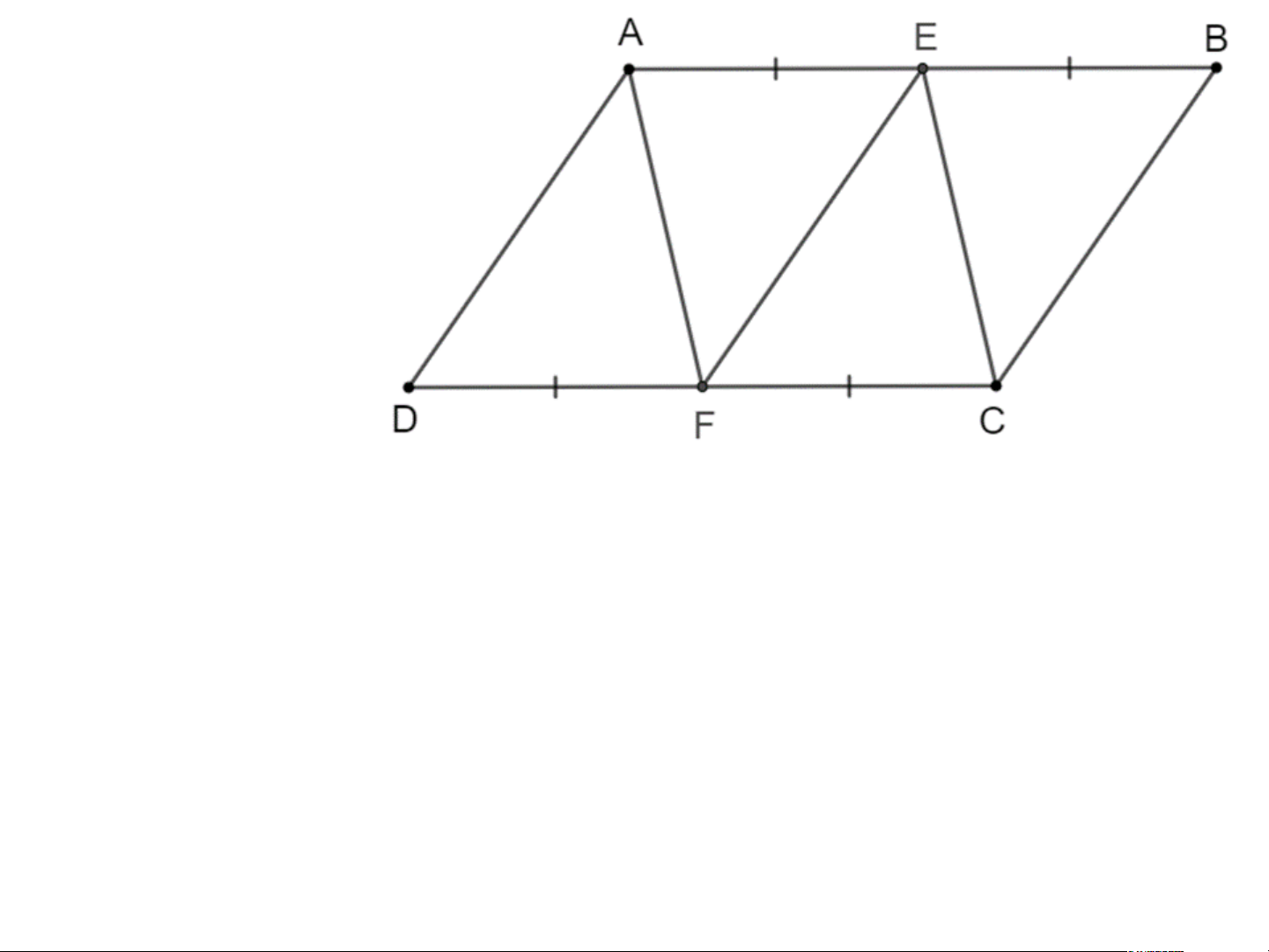
Bài 3.17 tr 61 Toán 8 Tập 1: Cho hình bình hành ABCD.
Gọi E, F lần lượt là trung điểm của các cạnh AB, CD. Chứng minh rằng:
a) Hai tứ giác AEFD, AECF là những hình bình hành;
b) EF = AD, AF = EC. Lời giải:
a) Vì ABCD là hình bình hành nên AB = CD, AB // CD.
Mà E, F lần lượt là trung điểm của AB,
CD nên AE = BE = AB, CF = DF = DC oD đó AE = BE = CF = DF. • Xét tứ giác AEFD có: AE // DF (vì AB // CD); AE = DF (chứng minh trên)
Do đó tứ giác AEFD là hình bình hành.
• Xét tứ giác AECF có: AE // CF (vì AB // CD); AE = CF (chứng minh trên)
Do đó tứ giác AECF là hình bình Vậy hai tứ giác AEFD,h àn AE h.
CF là những hình bình hành.
b) Vì tứ giác AEFD là hình bình hành nên EF = AD.
Vì tứ giác AECF là hình bình hành nên AF = EC. Vậy EF = AD, AF = EC.
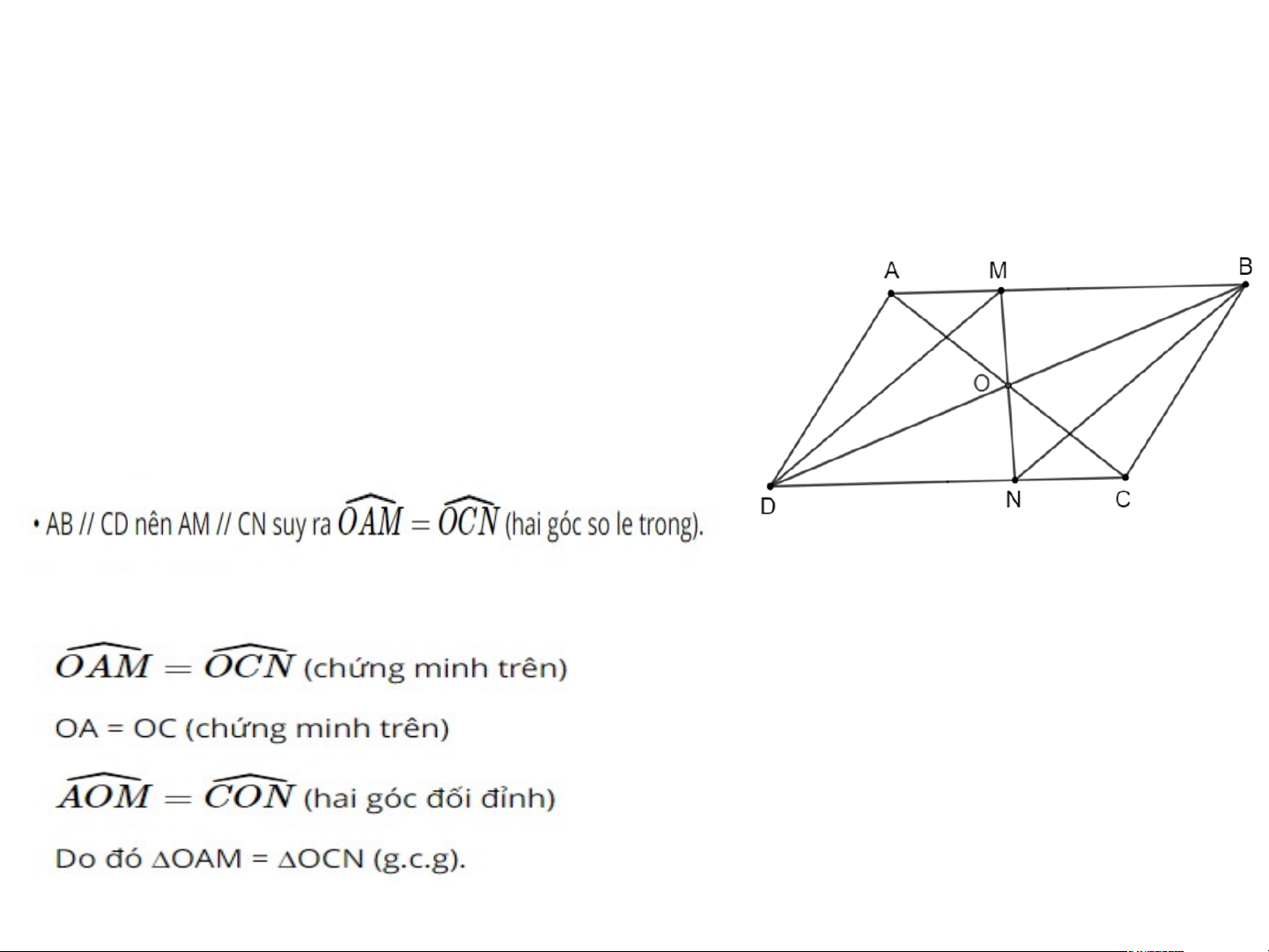
Bài 3.18 trang 61 Toán 8 Tập 1: Gọi O là giao điểm
của hai đường chéo của hình bình hành ABCD. Một đường
thẳng đi qua O lần lượt cắt các cạnh AB, CD của hình bình
hành tại hai điểm M, N. Chứng minh ∆OAM = ∆OCN. Từ
đó suy ra tứ giác MBND là hình bình hành. : Lời giải
Vì ABCD là hình bình hành nên ta có:
• Hai đường chéo AC và BD cắt
nhau tại O nên OA = OC, OB = OD. Xét ∆OAM và ∆OCN có:
Do đó ∆OAM = ∆OCN (g.c.g).
Suy ra AM = CN (hai cạnh tương ứng)
Mặt khác, AB = CD (chứng minh trên); AB = AM + BM; CD = CN + DN. Suy ra BM = DN. Xét tứ giác MBND có: • BM // DN (vì AB // CD) • BM = DN (chứng minh trên)
Do đó, tứ giác MBND là hình bình hành.
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12




