





Preview text:
CHÀO MỪNG CÁC EM
ĐẾN VỚI BÀI HỌC HÔM NAY! KHỞI ĐỘNG
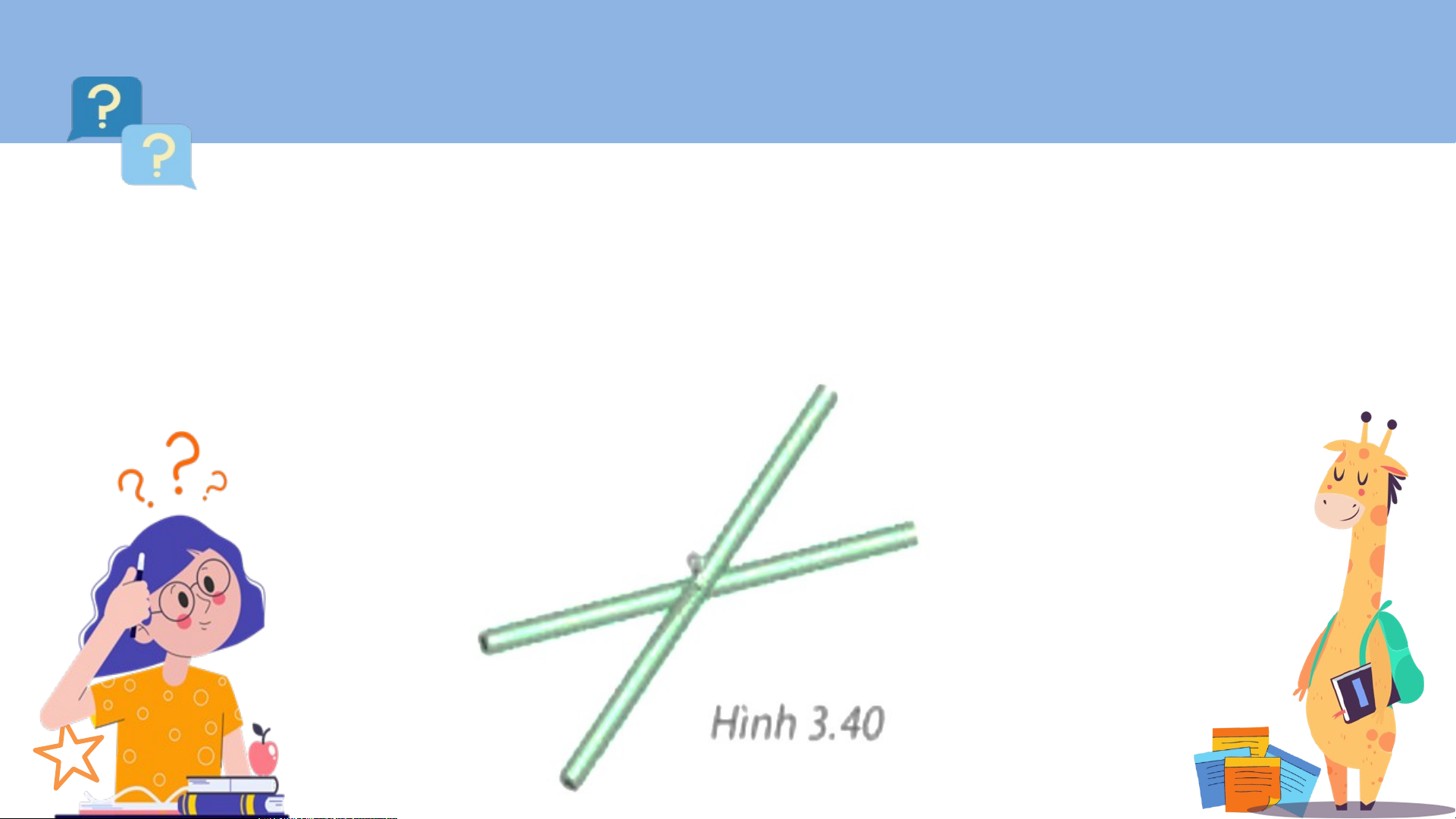
Hai thanh tre thẳng bằng nhau, được gắn với nhau tại trung điểm của
mỗi thanh. Khi các đầu mút của hai thanh tre đó tạo thành bốn đỉnh của
một tứ giác (H.3.40) thì tứ giác đó là hình gì? Tại sao?
BÀI 13. HÌNH CHỮ NHẬT
Thời gian thực hiện: 1 tiết Giáo viên: Nguyễn Hoàng Trung NỘI DUNG BÀI HỌC 01 Hình chữ nhật
02 Dấu hiệu nhận biết 1. H ình ì chữ ch nhật
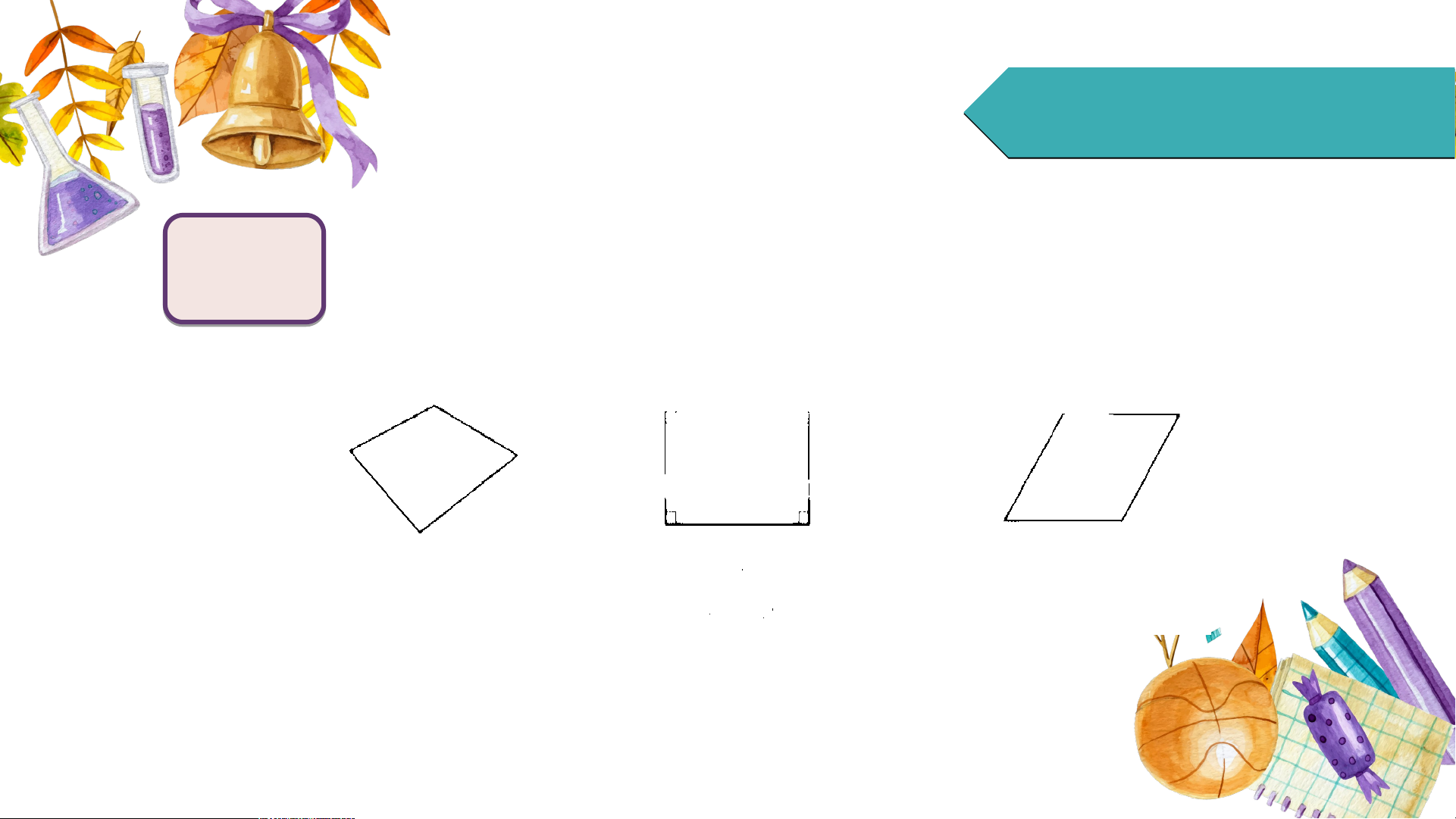
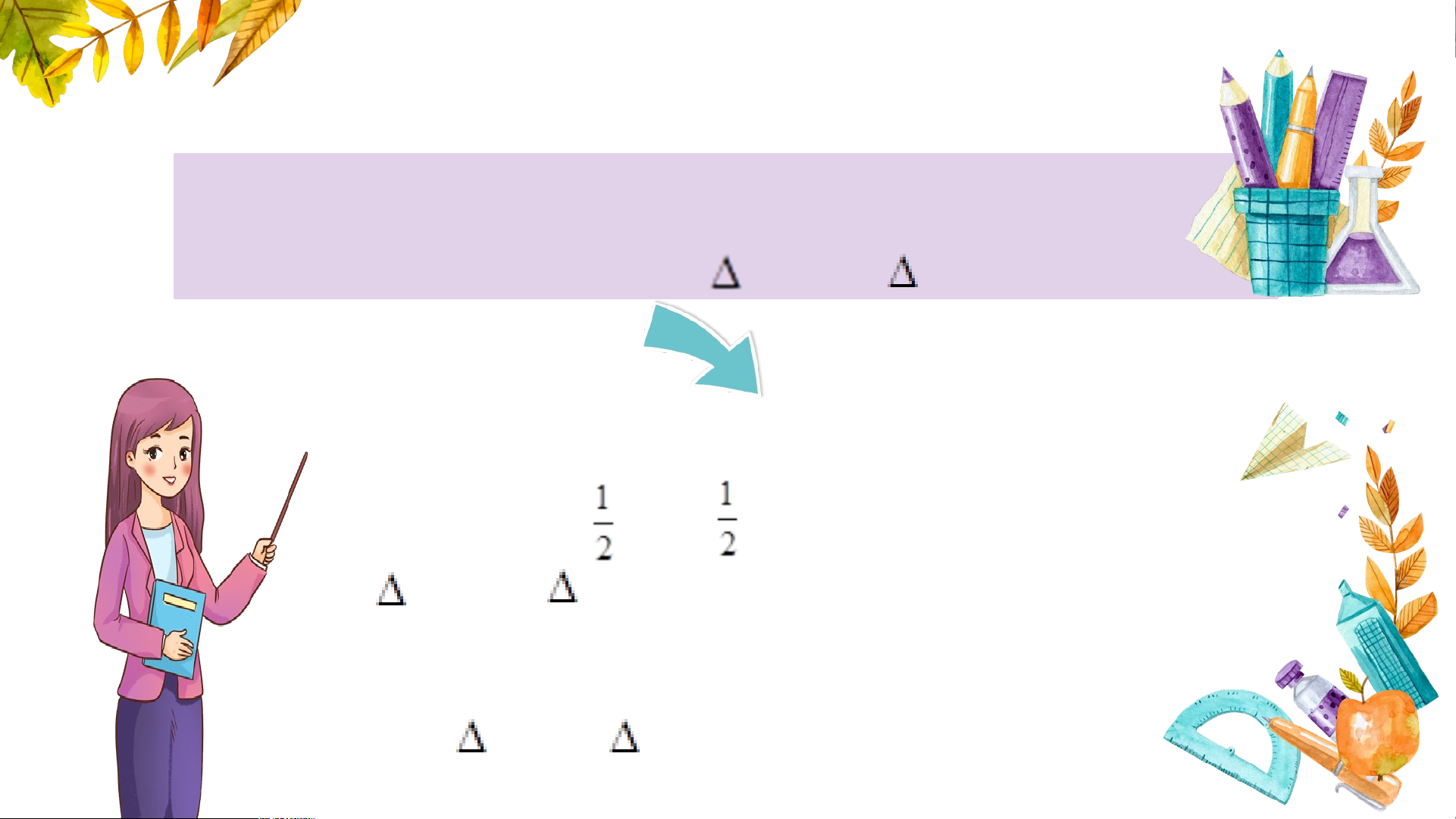
HĐ1 Trong các hình dưới đây, hình nào là hình chữ nhật? Tại sao?
Thế nào là hình chữ nhật?
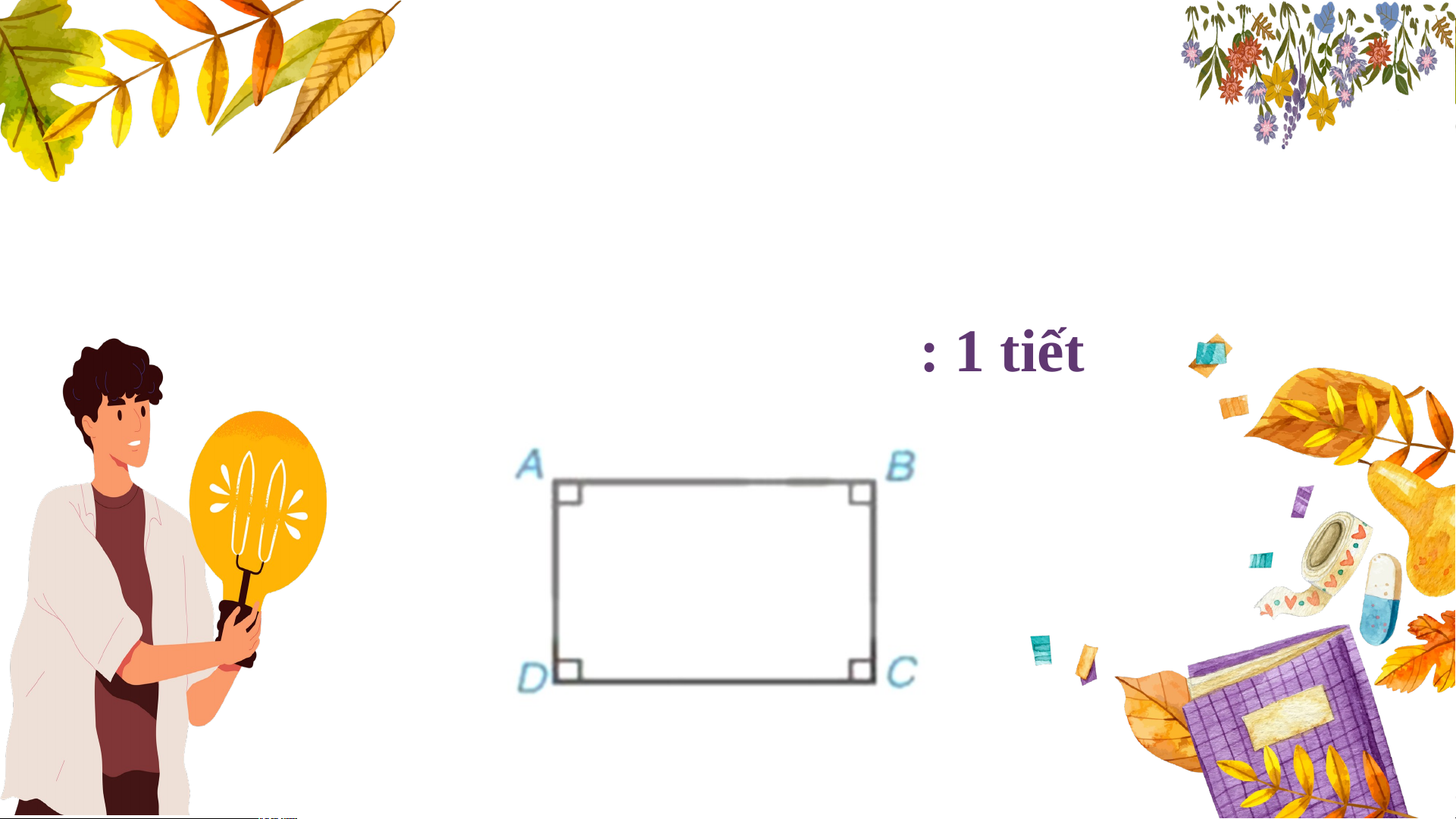
Định nghĩa: Hình chữ nhật là tứ
giác có bốn góc vuông HĐ2
Hình chữ nhật có là hình bình hành
không, có là hình thang cân không? Tại sao?
Hình chữ nhật vừa là hình thang cân, vừa
là hình bình hành. Vậy em có thể cho biết
hình chữ nhật có những tính chất nào? Định lí 1:
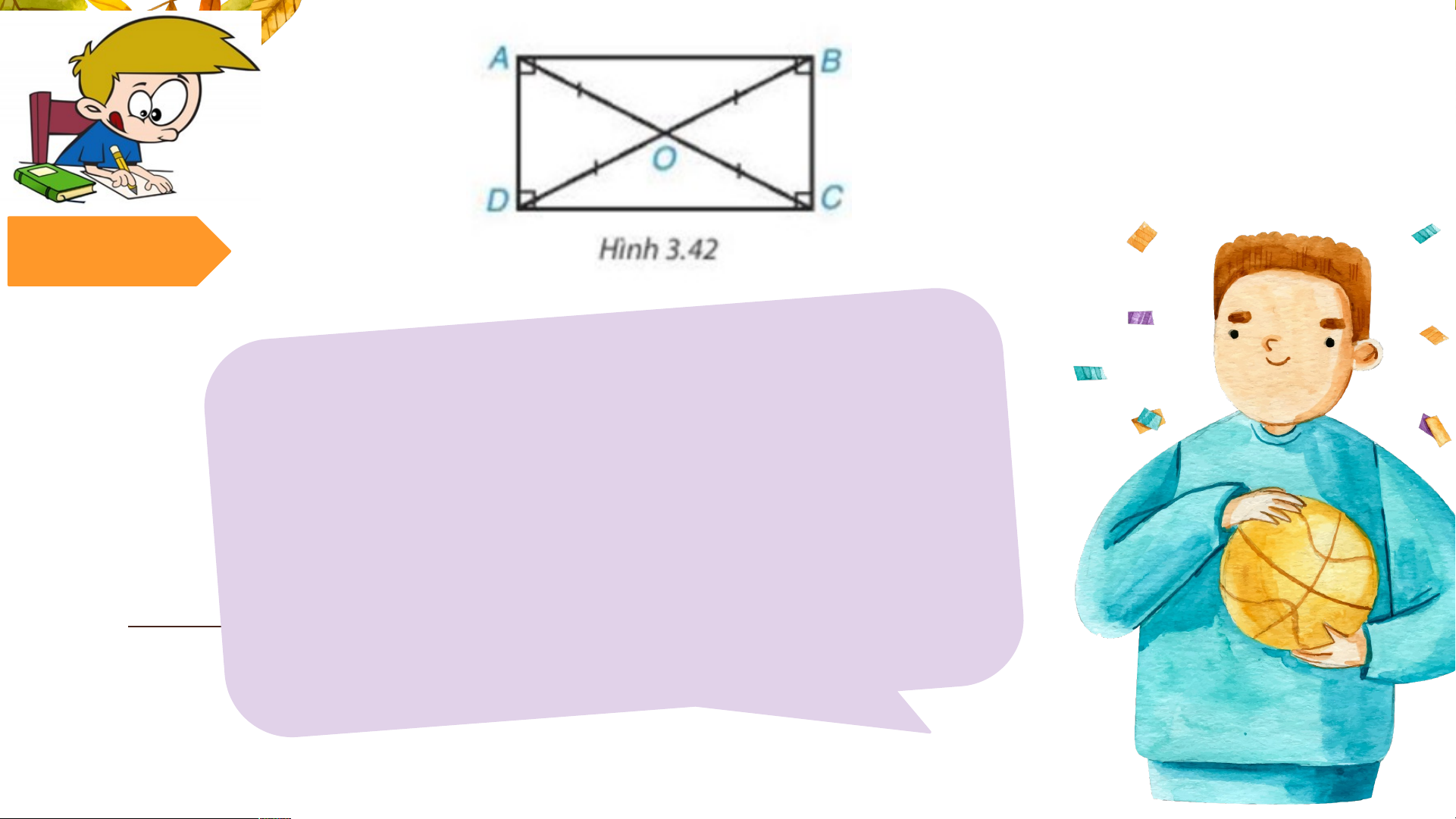
Trong hình chữ nhật, hai đường
chéo bằng nhau và cắt nhau tại
CREDITS: This presentation template was created by
Slidesgo, and includes icons by Flaticon, and infographics
trung điểm của mỗi đường (H3.42) & images by Freepik Tính Tính chấ chấ t hì t h nh c ình c h h ữ ữ nh n ậ hậtt::
+ Các cạnh đối bằng nhau.
+ Các góc đối bằng nhau.
+ Hai đường chéo bằng nhau. Hai đường
chéo cắt nhau tại trung điểm mỗi đường … Nhận xét
Trong tam giác vuông, đường trung
tuyến ứng với cạnh huyền bằng một
nửa cạnh huyền (Hình 3.42) Ví dụ 1:
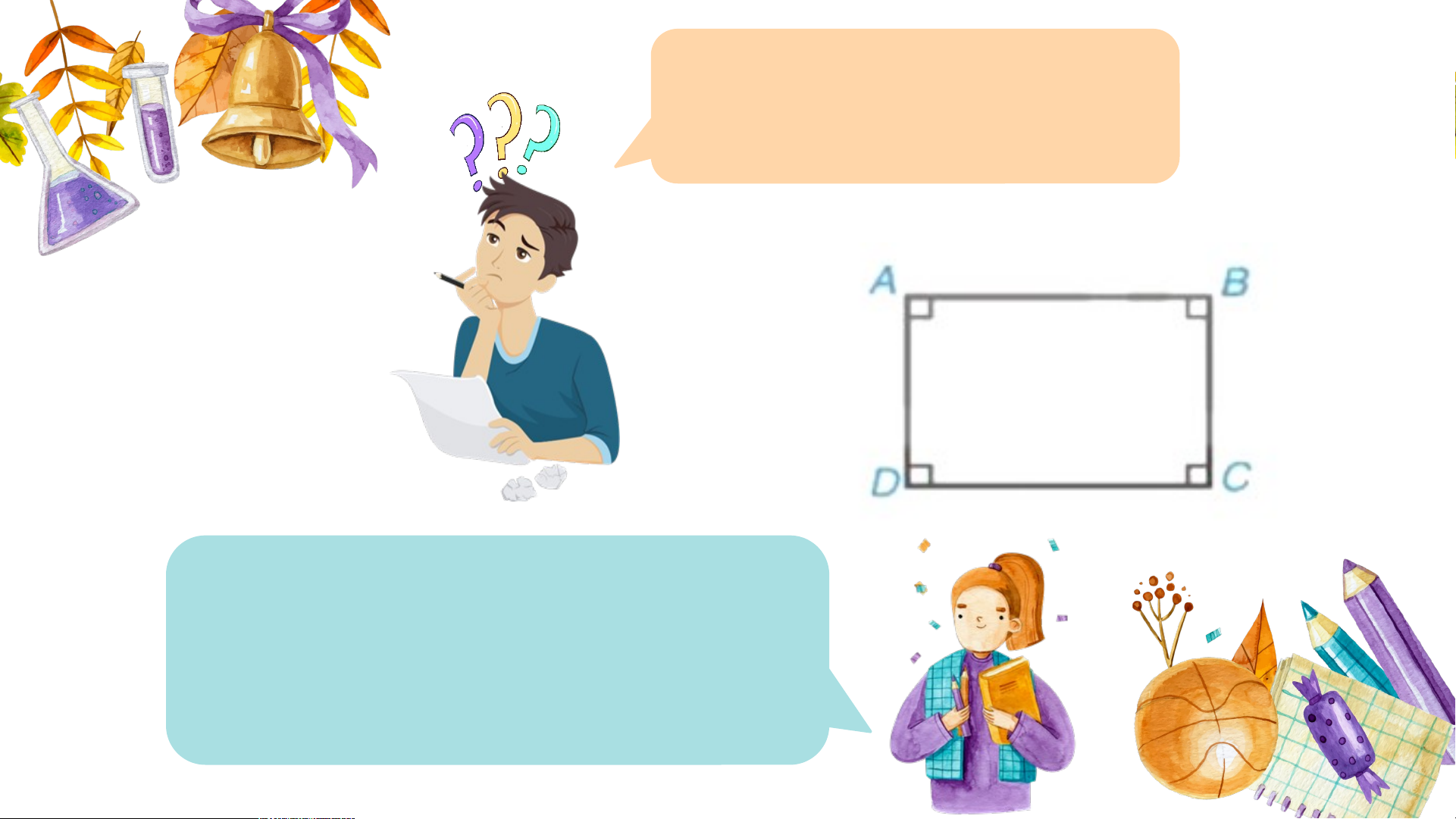
Cho hình chữ nhật ABCD, hai đường chéo AC và
BD cắt nhau tại O. Chứng minh OAB = ODC.
Vì ABCD là hình chữ nhật nên: OA = OC = AC = BD = OB = OD. OAB và ODC có: OA = OD, OB = OC, AB = CD. Vậy OAB = ODC (c.c.c). Luyện tập 1
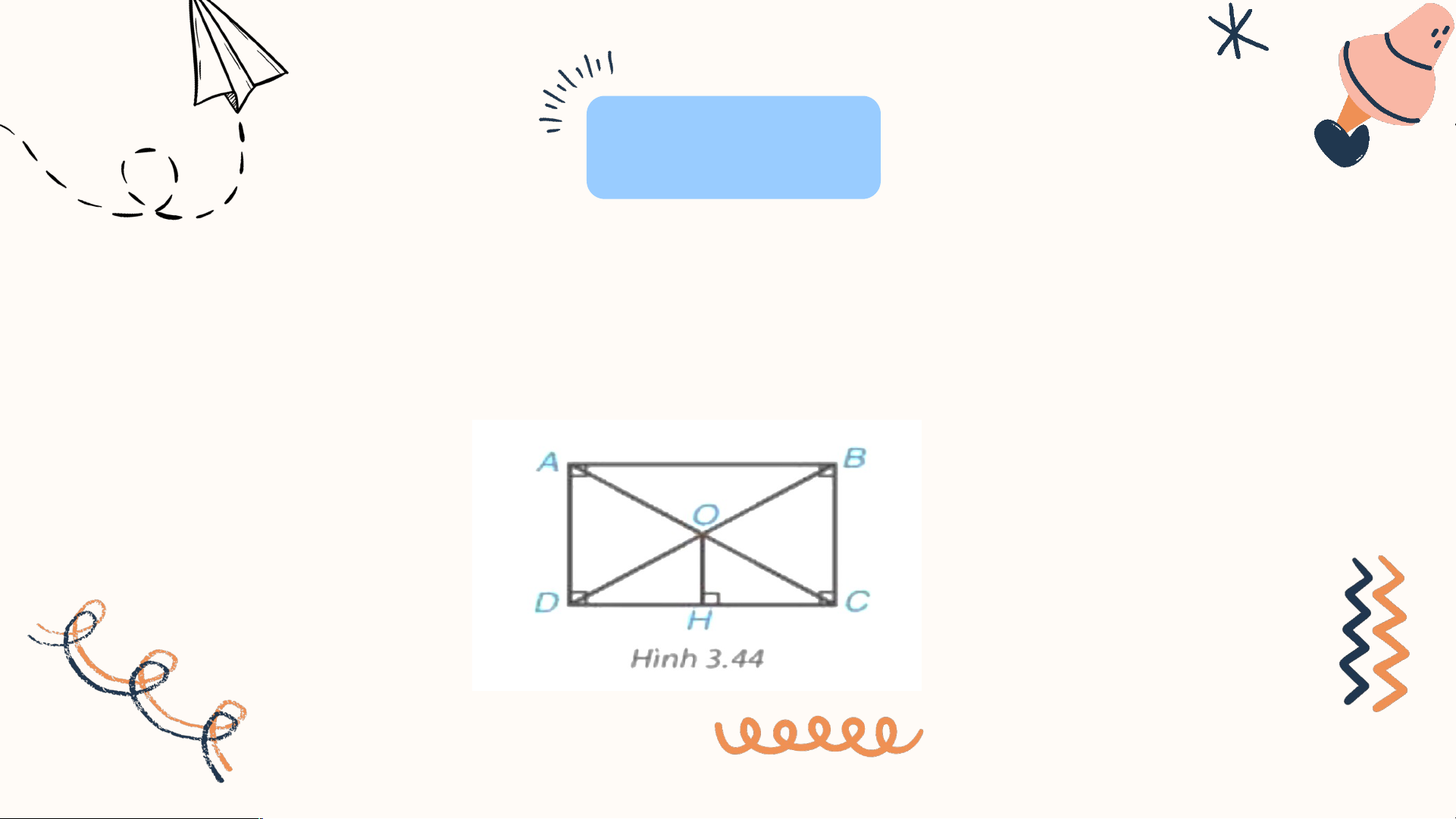
Cho hình chữ nhật ABCD. Hai đường chéo AC, BD cắt nhau tại O. Kẻ OH D
C (H.3.44). Chứng minh rằng H là trung điểm của DC. Giải
Xét hai tam giác vuông OHC và OHD có: OH chung
OD = OC (Tính chất hai đường chéo của hình chữ nhật)
2. Dấu hiệu nhận biết HĐ nhóm - 4HS
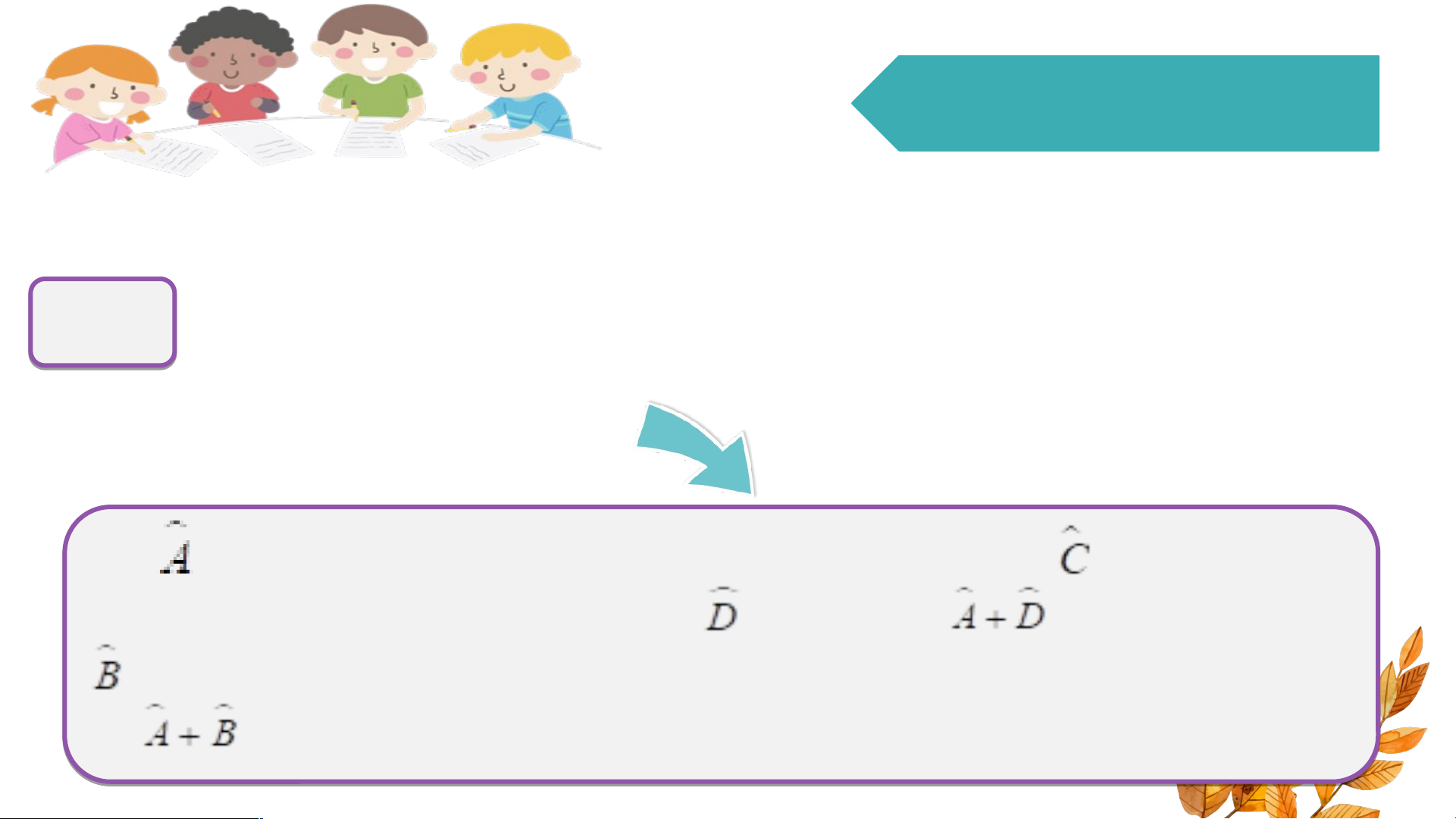
Tính các góc B, C, D. Tứ giác ABCD có là HĐ3
hình chữ nhật không? Vì sao?
Do = 90° và ABCD là hình bì h nh ình bì nh hà
h nh nên có = 90° (ha ( i góc đối icủa ủ hìn h h bình ìn h bình hà h nh), n = 90° do = 180° và = 90° do = 180°. V
°. ậy ABCD là hình c hìn hữ nhậ hữ nh t. Định lí 2
a) Hình bình hành có một góc vuông là hình chữ nhật.
b) Hình bình hành có hai đường
chéo bằng nhau là hình chữ nhật. Ví dụ 2.
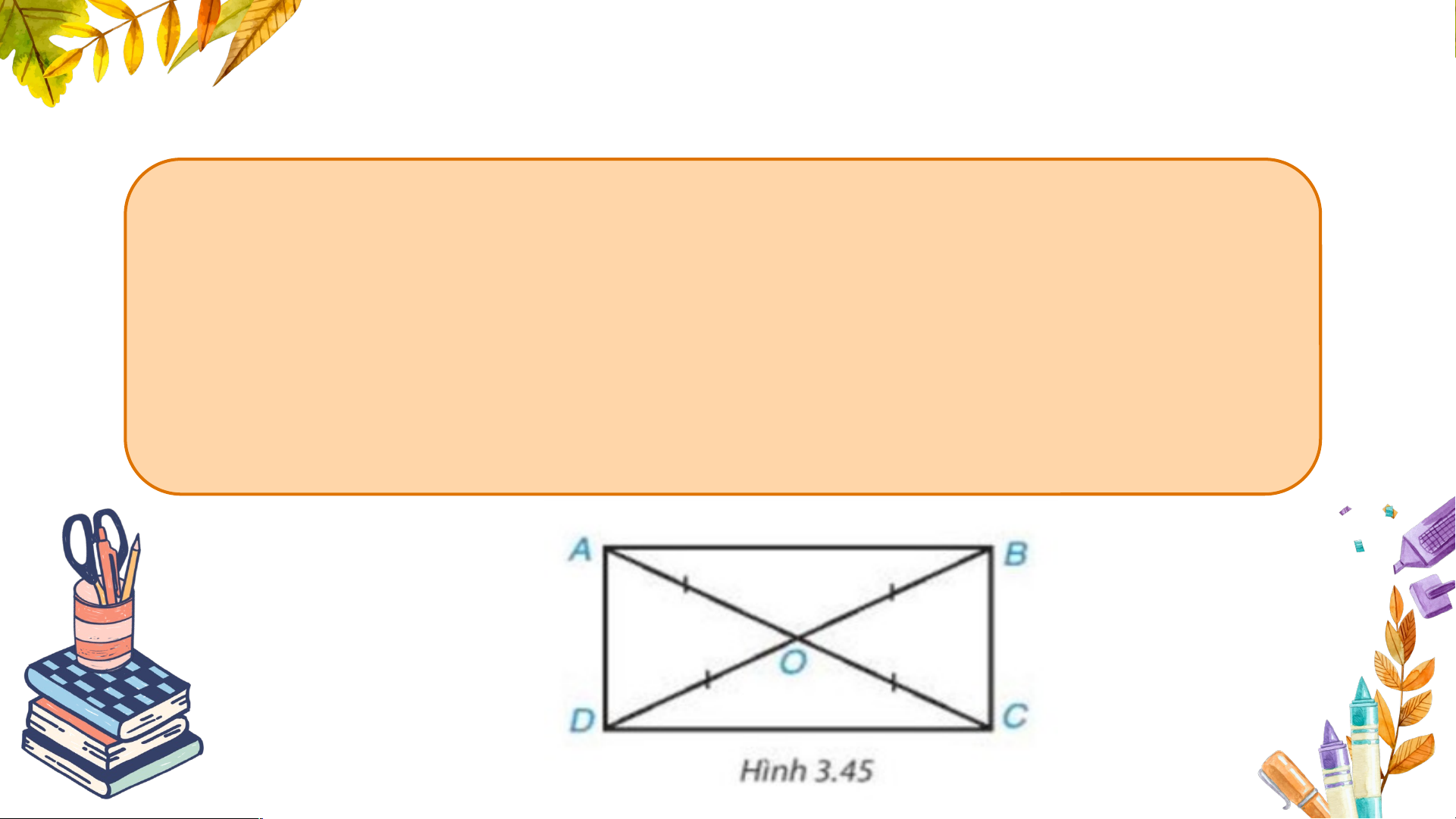
Chứng minh rằng tứ giác có hai đường chéo bằng
nhau và cắt nhau tại trung điểm của mỗi đường thì
tứ giác đó là hình chữ nhật.
ABCD là tứ giác; O là giao điểm của AC và BD GT AC = BD, OA = OC, OB = OD.
KL ABCD là hình chữ nhật. Chứng minh Theo The giả thiế o giả thi t, O ết, O là trung là tr ung đ iểm đ của cả iểm của A cả C A và C v à B D B n D ên ta c nên ó ta có AB A CD B là hình bình CD là hình bình h ành hàn . h. Hơn nữ Hơ a n nữ , a A , C A = C = B D B nê D n n t ên heo theo Đị nh lí Đị 2 nh lí , 2 hình , hìn bìn h bì h hàn nh hà h nh AB A CD B là hình chữ CD là hình nh chữ n ật. hật. Luyện tập 2
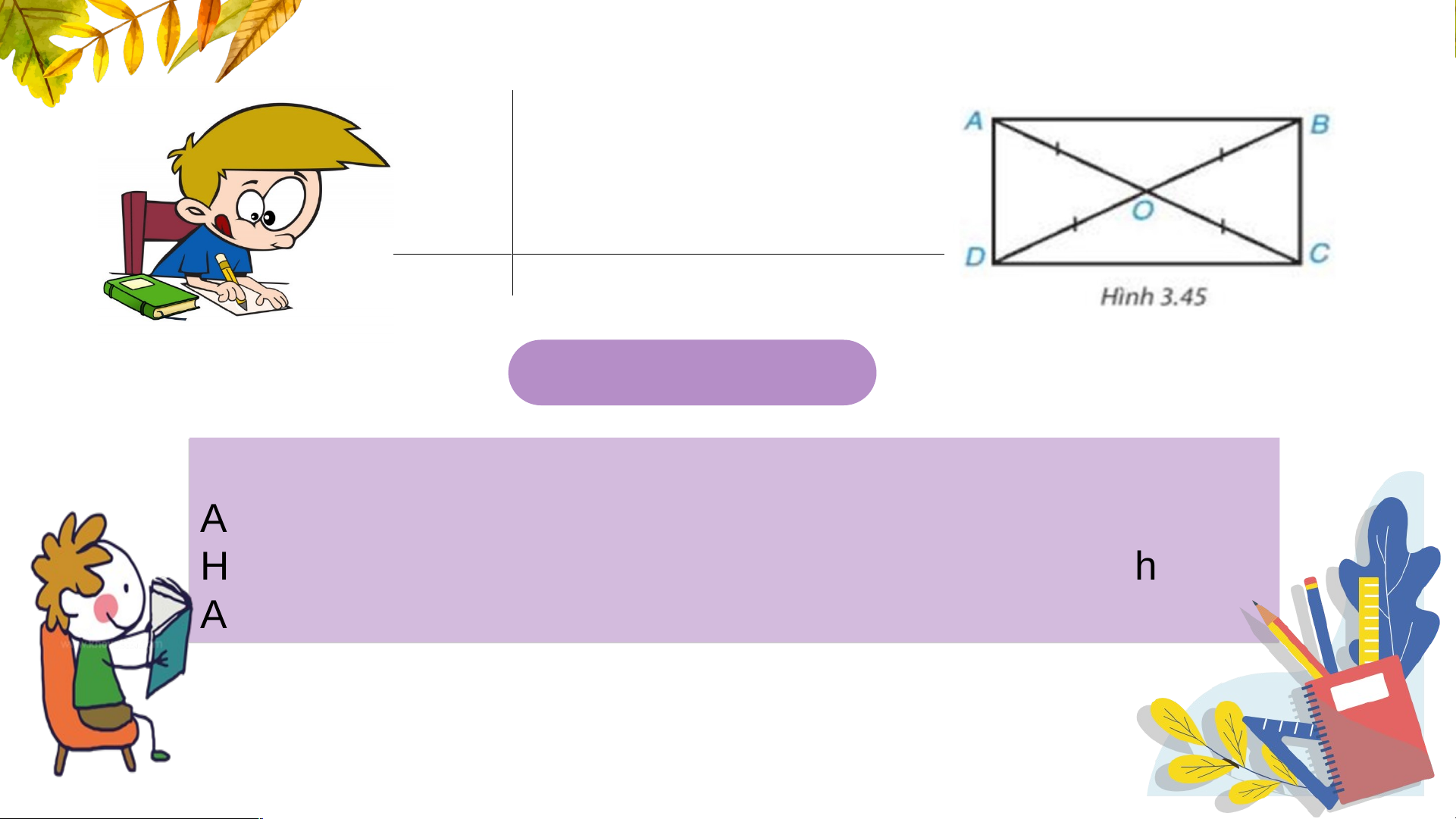
Cho tứ giác ABCD có = 90°, hai đường chéo
cắt nhau tại trung điểm O của mỗi đường. Hỏi
tứ giác ABCD là hình gì? Tại sao? Nhận xét:
Nếu tam giác có một đường trung tuyến bằng nửa cạnh
tương ứng thì tam giác đó là tam giác vuông.
Vận dụng: Giải quyết tình huống mở đầu.
Hai thanh tre thẳng bằng nhau, được gắn với nhau tại
trung điểm của mỗi thanh. Khi các đầu mút của hai
thanh tre đó tạo thành bốn đỉnh của một tứ giác (H.3.40)
thì tứ giác đó là hình gì? Tại sao? LUYỆN TẬP
Bài 3.25 (Sgk trang 66). Bằng ê ke, nêu cách kiểm tra
một tứ giác có là hình chữ nhật hay không. Hãy giải thích kết quả. HĐ nhóm đôi
Vì tổng bốn góc của tứ giác
bằng 3600 , nên nếu ba góc của
Khi dùng ê ke kiểm tra được
một tứ giác là góc vuông thì tứ
ba góc của tứ giác là góc vuông
giác đó có bốn góc là góc
thì tứ giác là hình chữ nhật.
vuông, vậy nó là một hình chữ nhật. LUYỆN TẬP
Bài 3.26 (Sgk trang 66). Bằng compa, nêu cách kiểm
tra một tứ giác có là hình chữ nhật hay không. Giải thích kết quả. HĐ nhóm đôi
Dùng compa kiểm tra từng cặp cạnh
đối có bằng nhau không và hai
đường chéo có bằng nhau không.
Bài 3.27 (Sgk trang 66). Cho tam giác ABC, đường cao AH.
Gọi M là trung điểm của AC, N là điểm sao cho mà trung
điểm của HN. Chứng minh tứ giác AHCN là hình chữ nhật. Chứng minh HĐ nhóm 4 – 6 HS
- Tứ giác AHCN có hai đường chéo AC, HN cắt
nhau tại trung điểm của mỗi đường nên là một hình bình hành.
- Hình bình hành AHCN có nên là hình chữ nhật
(Dấu hiệu nhận biết h.c.n) Bài 3.28 (S Bài gk 3.28 (S tr gk an tr g 66) an . X g 66). ét X m ét ột điể một đm M iể tr m M ên tr c ênạn c h h ạnh uyề hu n c yềnủa tam gi củ ác a tam gi ác ABC A v BCu ôn vu g c ôn ân g c tại ân A tại . G A ọi . G N ọi và P N lần và P l lượt ần l là h ượt l ìn à h hì c nhhi c ếhui vu ếu ôn vu g góc ôn c g gócủa của M tr M ên tr c ênác c c ácạn c h ạnA h BA và B A và CA.C. a) H a) ỏi H tứ ỏi t gi ứ ác gi M ác PA MPNA là h N l ìn à h hì gì nh ? gì? b) H b ỏi ) H M ỏi ở vị M tr ở vị í n trí ào th n ì ào t đ hì oạn đ th oạn ẳn th g N ẳn P c g NPó đ c ộ d ó đ ài ộ d n ài gắn n n gắn hất nh ? ấtV ? ì s Vìao s ? a o? HĐ nhóm 4 – 6 HS Chứng minh a) Tứ a) T giác ứ gi M ác P M A P N A c N ó b c a góc ó b vu a góc ôn vu g tại ông tạ iA, N A , , N P n , P ê n n ê l n à m l ột h à một ì h n ì h n h ch c ữ n h h ữ n ật. hật. b) b) H ai H đ ai ườ đ ng c ường h c é h o é A o M A , N M P , N c P ủ c a h ủ ì a h n ì h n c h h c ữ n h h ữ n ật h MP ật M A P N A b N ằn b g n ằng h n au h au tức tức là N l P à N = P = AM A . M Kẻ K ẻ AH A H BC B C A M A M A H A (A H H (A H là k l h à k oản h g c oản ác g c h ác từ h A từ đ A ế đ n ế BC n ) BC) N P N P A H A N P N P nh n ỏ n h h ỏ n ất h = ất = AH A h H a h y M ay M H . H
HƯỚNG DẪN VỀ NHÀ 01 02 03 Ôn lại kiến Hoàn thành bài tập Chuẩn bị thức đã học về trong SBT. bài mới. hình chữ nhật. CẢM ƠN CÁC EM
ĐÃ CHÚ Ý LẮNG NGHE BÀI HỌC!
Document Outline
- Slide 1
- Slide 2
- BÀI 13. HÌNH CHỮ NHẬT Thời gian thực hiện: 1 tiết
- 02
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Luyện tập 2
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25