








Preview text:
KHỞI ĐỘNG
Chỉ ra câu đúng , sai ? Câu Đúng, Sai
1. Hình bình hành là tứ giác có các cạnh đối song Đ song.
2. Tứ giác có hai cạnh đối bằng nhau là hình bình S hành
3. Tứ giác có hai cạnh đối song song và bằng
nhau là hình bình hành. Đ
4. Hình bình hành có các góc đối bằng nhau. Đ
5. Hình bình hành có hai đường chéo bằng nhau S
6. Tứ giác có các cạnh đối song song là hình bình hành. Đ | | | | | Tứ Có 4 cạnh bằng | giác nhau
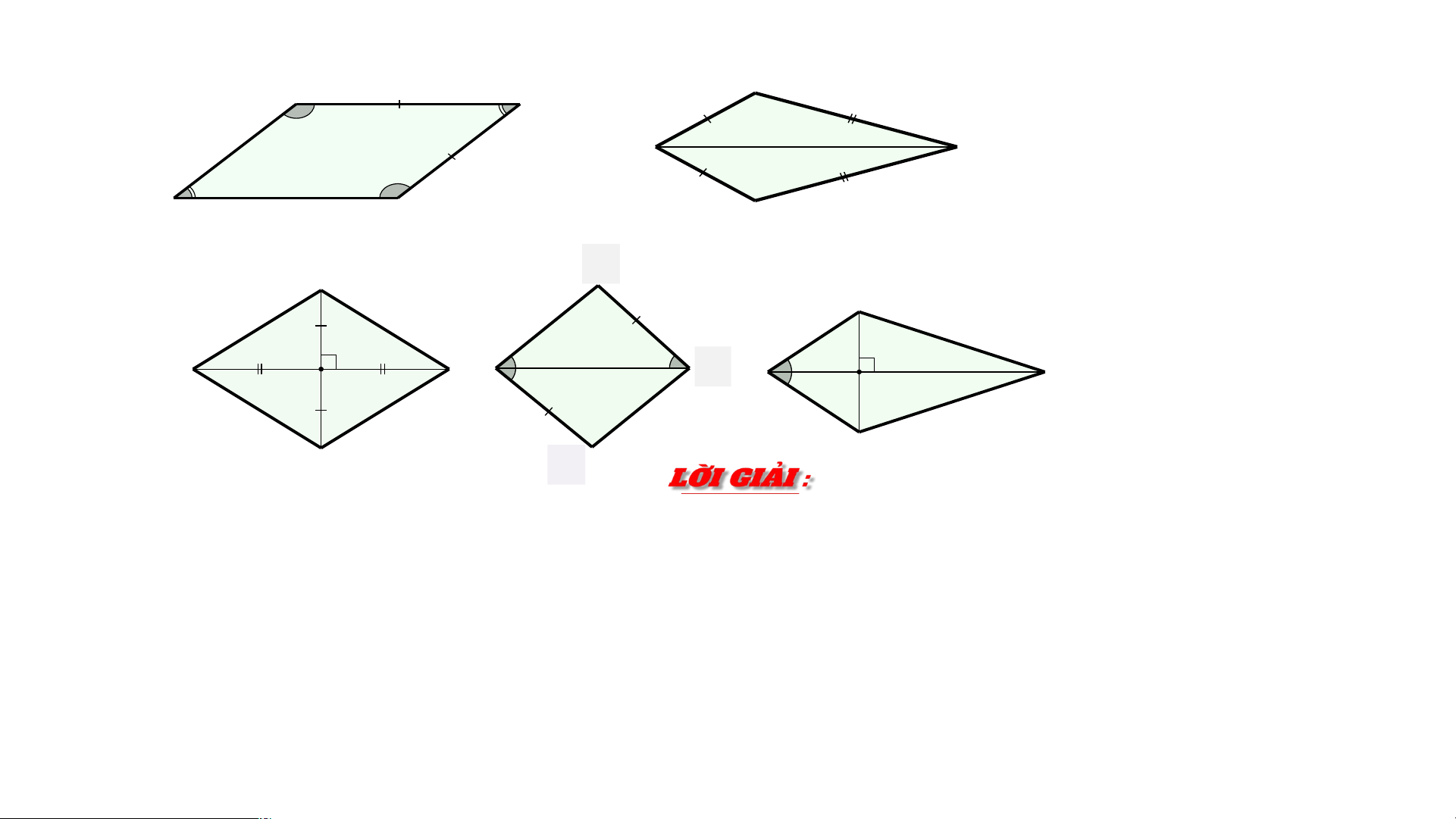
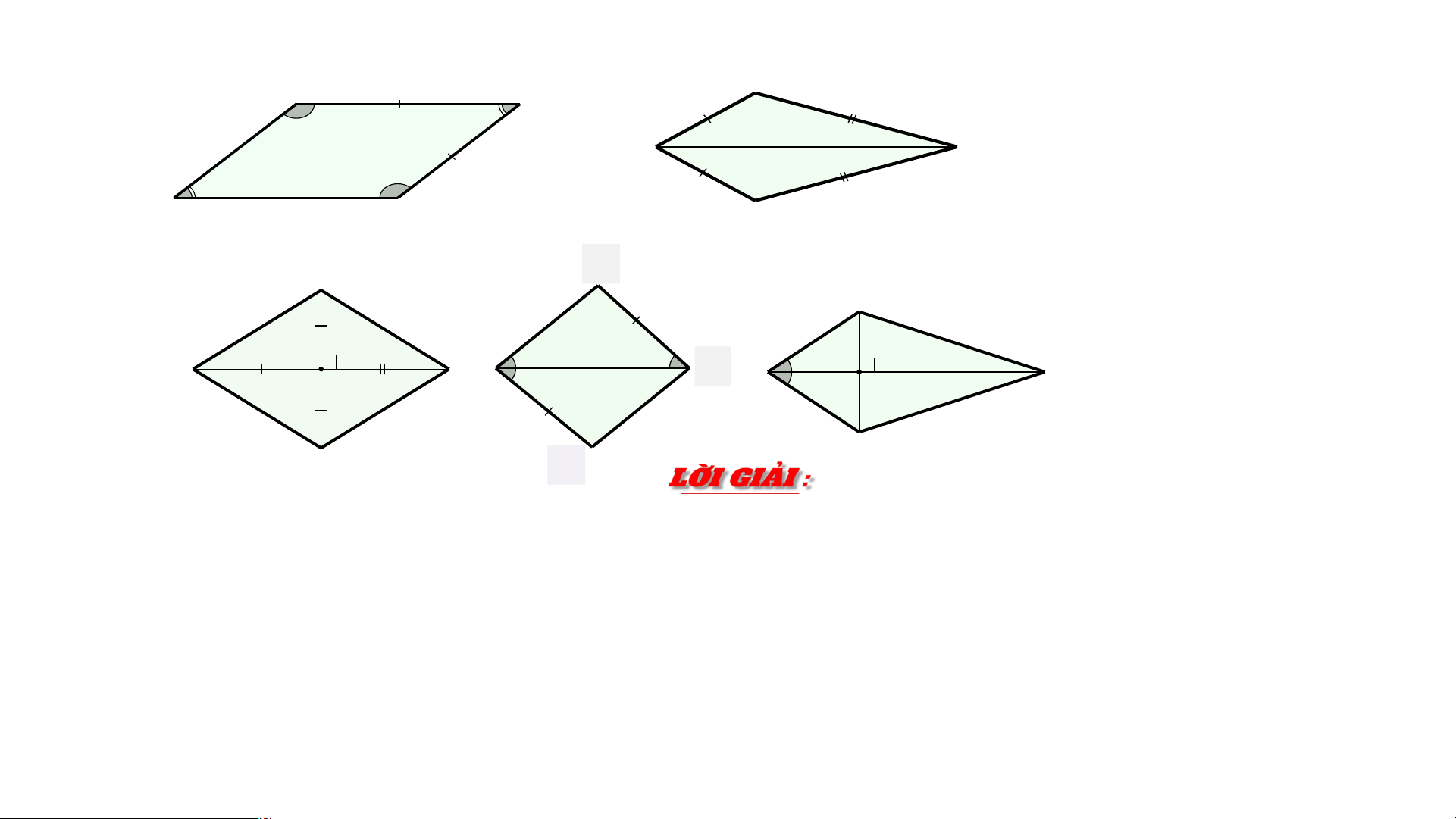
Có hai cạnh kề bằng nhau Hình bình Có hai đường chéo hành vuông góc với nhau Có 1 đư p ờ h n â g n c g h i é á o c l c à ủ đ a ư 1 ờ n g g ó c ))
Lấy một tờ giấy, gấp làm tư tạo ra một góc A
vuông O, đánh dấu hai điểm A, B trên hai cạnh góc
vuông rồi cắt chéo theo đoạn thẳng AB (H.3.46a).
Sau khi mở tờ giấy ra, ta được một tứ giác. B O a) Hình 3.46 A B O b) 1 . HÌNH TH TH OI
Khái niệm hình thoi và tính chất của nó. B a. Định nghĩa : A C D
* Hình thoi cũng là hình bình hành.
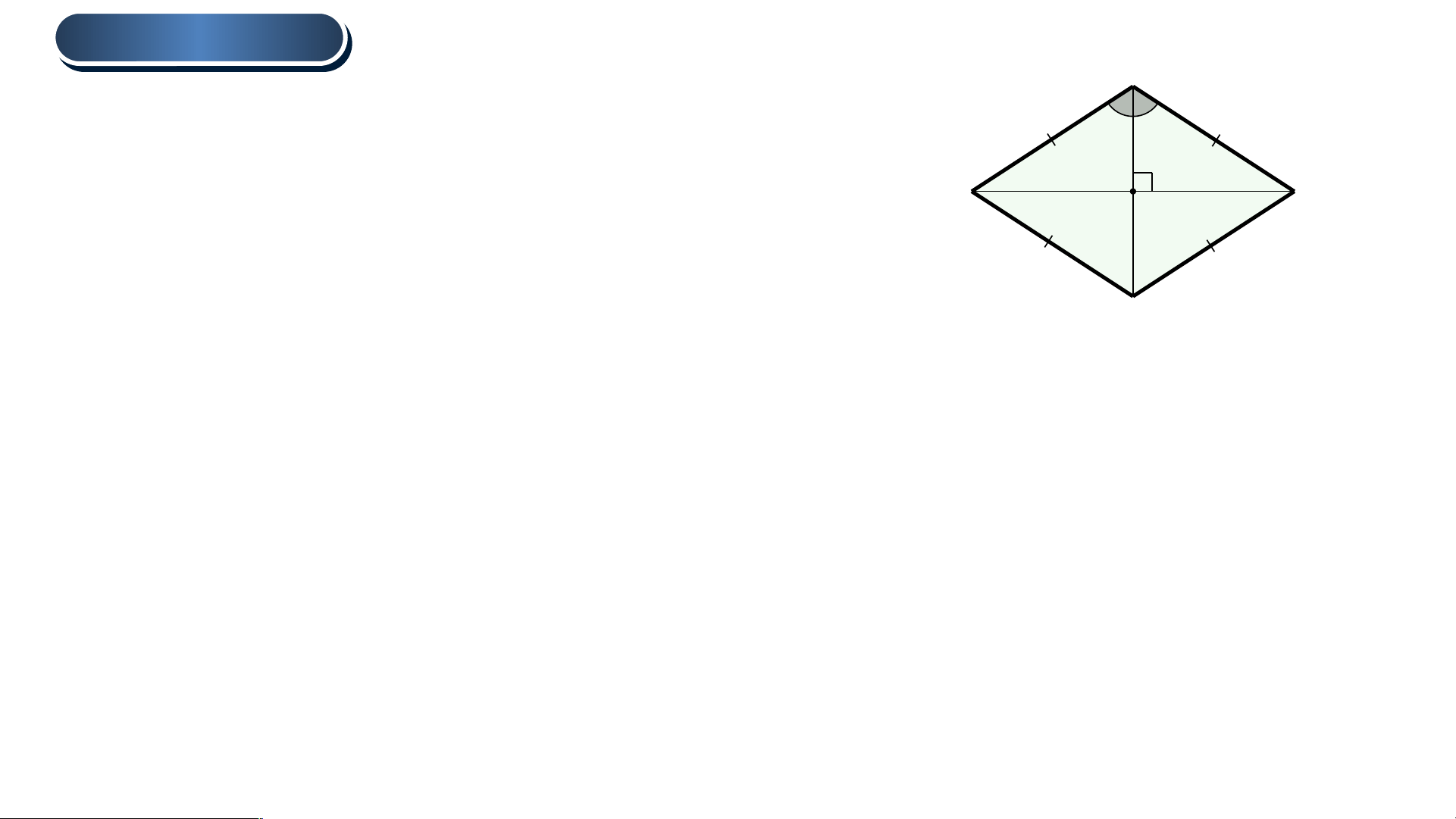
b. Tính chất của hình thoi : B Trong hình thoi : A || || ( C ) O
- Có bốn cạnh bằng nhau.
- Các cạnh đối song song. D
- Các góc đối bằng nhau.
- Hai đường chéo cắt nhau tại trung điểm của mỗi đường. 1 . HÌNH TH TH OI
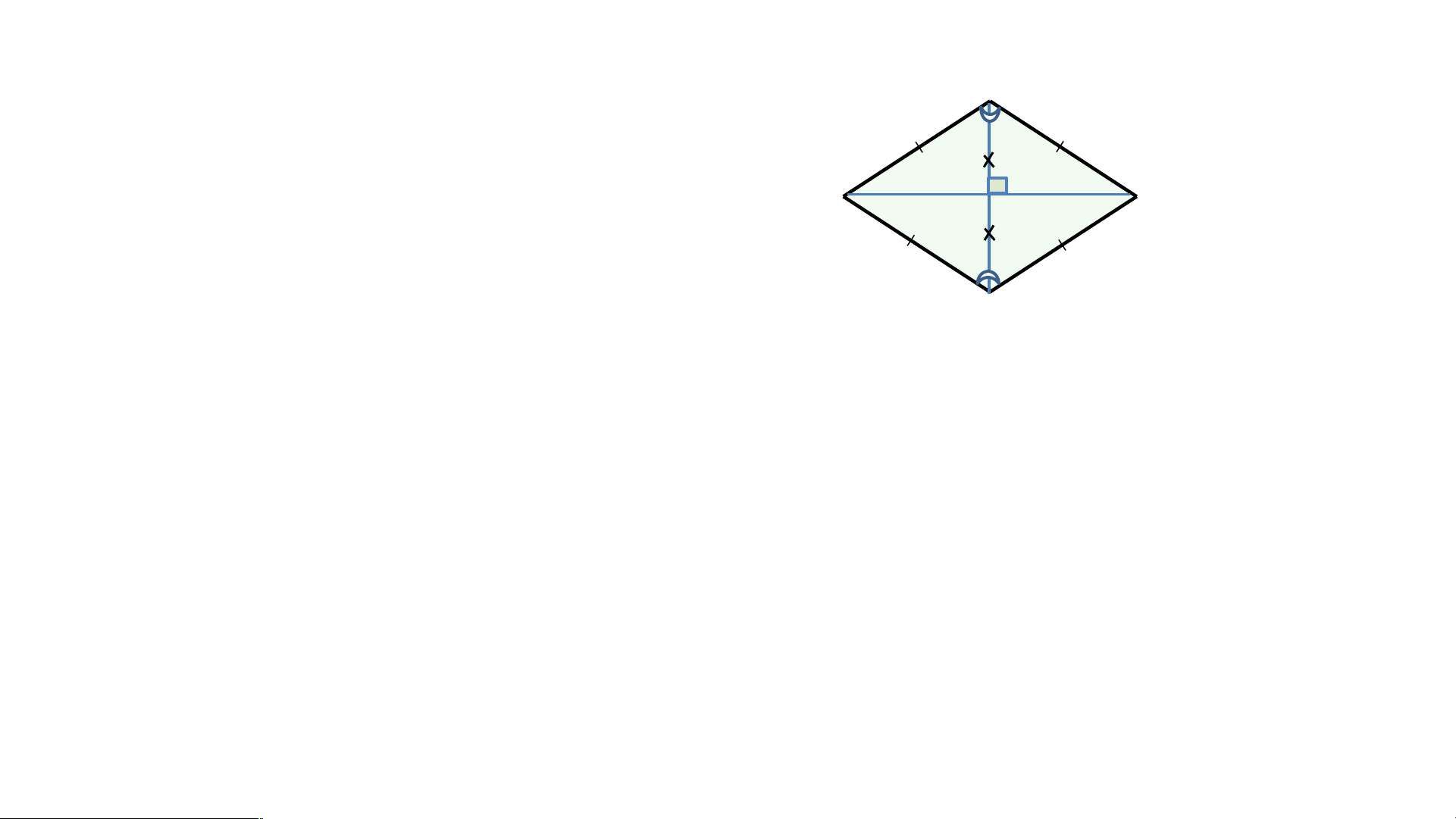
Tính chất về hai đường chéo của hình thoi.
Cho hình thoi ABCD có 2 đường chéo AC, BD cắt nhau tại O (H.3.48).
a) Tam giác ABC có cân tại B không?
b) AC có vuông góc với BD không và BD có là đường phân giác của góc B không? Vì sao? B
a) Vì tứ giác ABCD là hình thoi nên AB = BC. 1 2 1 2
Suy ra ∆ABC cân tại B. A C 2 O 1
b. Vì ∆ABC cân tại B, có BO là đường trung tuyến nên 1 2
BO cũng là đường cao, đường phân giác. D Suy ra B O A C hay B D A
C và BD là đường phân Hình 3.48 giác góc B
b. Tính chất của hình thoi : B Trong hình thoi : A || || ( C ) O
- Có bốn cạnh bằng nhau.
- Các cạnh đối song song. D
- Các góc đối bằng nhau.
- Hai đường chéo cắt nhau tại trung điểm của mỗi đường.
* Định lí 1 : Trong hình thoi :
- Hai đường chéo vuông góc với nhau.
- Hai đường chéo là các đường phân giác của các góc trong hình thoi. 1 . HÌNH TH TH OI B
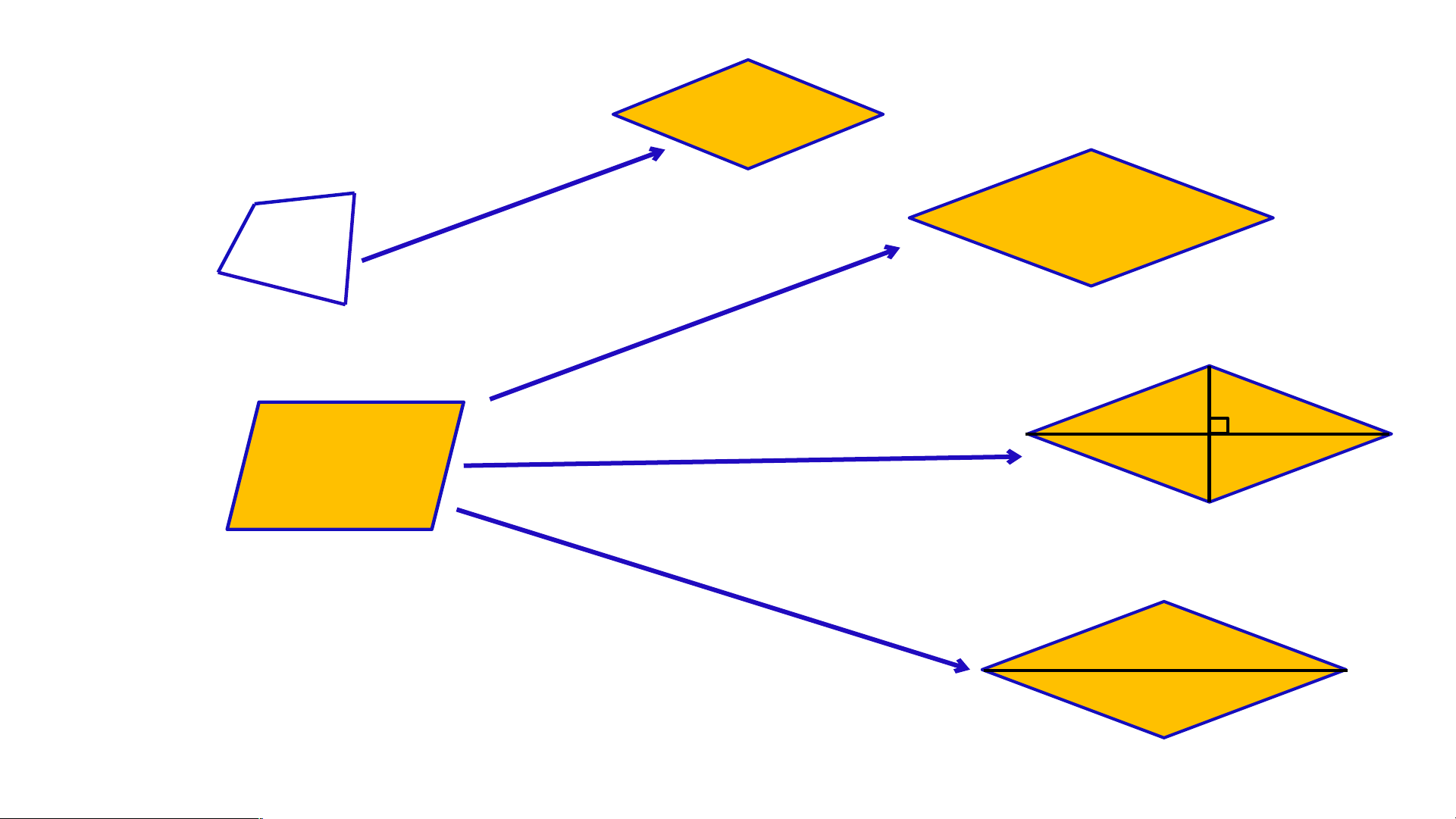
Dấu hiệu nhận biết hình thoi. 1 2 A C
1. Tứ giác có bốn cạnh bằng nhau là hình thoi. O
Định lí 2 : D
2. Hình bình hành có hai cạnh kề bằng nhau là hình thoi.
3.Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.
4. Hình bình hành có một đường chéo là đường phân
giác của một góc là hình thoi.
Dấu hiệu nhận biết hình thoi. | | Hình thoi | | | Tứ Có 4 cạnh bằng Hình thoi | giác nhau
Có hai cạnh kề bằng nhau Hình bình Có hai đường chéo Hình thoi hành vuông góc với nhau Có 1 đư p ờ h n â g n c g h i é á o c l c à ủ đ a ư 1 ờ n g g ó c ) Hình thoi ) 1 . HÌNH TH TH OI
Dấu hiệu nhận biết hình thoi.
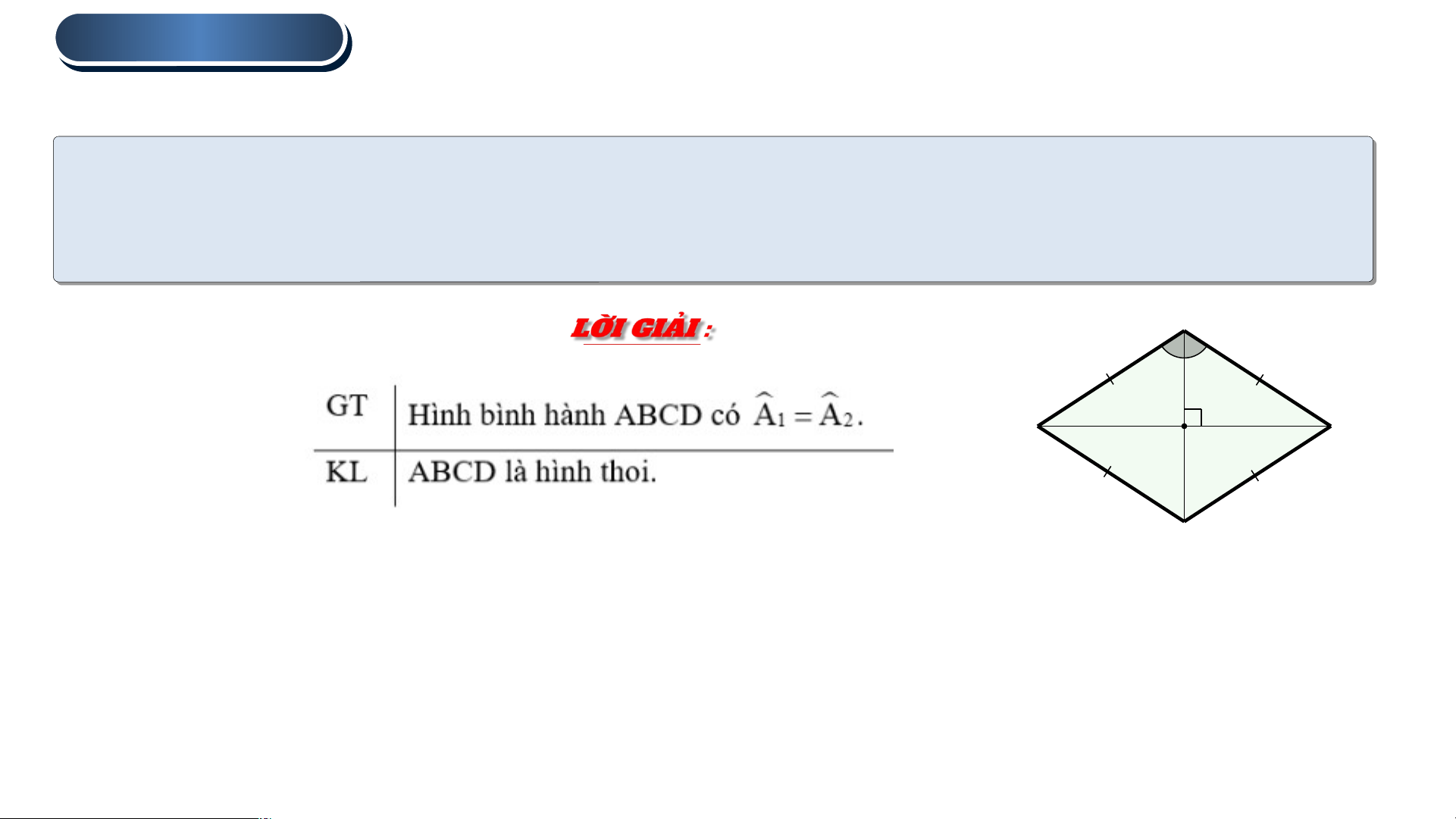
Câu hỏi : Hãy viết giả thiết, kết luận của câu 4 trong Định lí 2. A 1 2 D B O C
Bài tập 1. Tứ giác nào là hình thoi ? N A B M P D C Q A E G G 2 1 H I D BF 1 S P R K C c) b) a) T
a) Tứ giác ABCD là hình bình hành vì có các góc đối bằng nhau : ,
Mặt khác , ta lại có hai cạnh kề AB và BC bằng nhau
Do đó, tứ giác ABCD là hình thoi.
b) Tứ giác MNPQ không phải là hình thoi vì hai cạnh
kề MN và NP không bằng nhau.
Bài tập 1. Tứ giác nào là hình thoi ? N A B M P D C Q A E G G 2 1 H I D BF 1 S P R K C c) b) a) T
+ Tứ giác GHIK có hai đường chéo cắt nhau tại trung điểm của mỗi đường và
chúng vuông góc với nhau nên tứ giác đó là hình thoi.
+ Vì , mà hai góc này ở vị trí so le trong nên EF // DT.
Mà EF = DT nên tứ giác DEFT là hình bình hành.
Mặt khác hay DF là tia phân giác của . Do đó DEFT là hình thoi.
+Tứ giác GPRS không phải là hình thoi vì các cạnh không bằng nhau.
Bài tập 2. Hai đường tròn tâm A và C cùng bán kính, cắt nhau tại B,D.
a. Tứ giác ABCD là hình gì ? Tại sao ? b. Chứng minh BD
c. Chứng minh AC là tia phân giác của góc BAC. B
a) Vì hai đường tròn tâm A và C có cùng bán kính,
cắt nhau tại B, D nên AB = AD = CD = CB A C
Vậy theo định nghĩa, tứ giác ABCD là hình thoi D
b) Từ câu a và theo định lí 1 ta có BD Hình 3.49
c) Vì ABCD là hình thoi suy ra AC là tia phân giác của góc BAC
HƯỚNG DẪN VỀ NHÀ
+ Học và ghi nhớ định nghĩa, tính chất, dấu hiệu nhận biết hình thoi.
+ Vận dụng làm bài tập 2.29; 3.30;3.31 (sgk/ tr 36)
+ Tìm hiểuđịnh nghĩa, tính chất, dấu hiệu nhận biết hình vuông thức tiếp theo.
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16




