27 trang 75 lượt tải

Giáo án điện tử Toán 8 Bài 15 Kết nối tri thức: Định lí Thalès trong tam giác

149

Bài giảng PowerPoint Toán 8 Bài 15 Kết nối tri thức: Định lí Thalès trong tam giác hay nhất, với thiết kế hiện đại, dễ dàng chỉnh sửa giúp Giáo viên có thêm tài liệu tham khảo để soạn Giáo án Toán 8. Mời bạn đọc đón xem!

Chủ đề: Bài giảng điện tử Toán 8 206 tài liệu

Môn: Toán 8 1.9 K tài liệu

Sách: Kết nối tri thức

Tác giả:

Profile

Tin Hin

1 năm trước
Danh sách Quiz
/27
Cây cầu AB bắc qua một con sông có chiều
rộng 300 m. Để đo khoảng cách giữa hai điểm C
và D trên hai bờ con sông, người ta chọn một
điểm E trên đường thẳng AB sao cho ba điểm E,
C, D thẳng hàng. Trên mặt đất, người ta đo được
AE = 400 m, EC = 500 m.
Theo em, người ta tính khoảng cách
giữa C và D như thế nào?
1 . ĐOẠN THẲNG TỈ LỆ
1 . ĐOẠN THẲNG TỈ LỆ
Tỉ số của hai đoạn thẳng
Cho các đoạn thẳng như Hình 4.2 .
Hãy tìm độ dài của hai đoạn thẳng AB và CD nếu chọn đoạn
MN làm đơn vị độ dài. Với các độ dài đó hãy tính tỉ số
Chọn đoạn MN làm đơn vị độ dài
thì MN = 1 (đvđd).
D
C
B
A
N
M
Hình 4.2
Khi đó, AB = 2 (đvđd)
CD = 6 (đvđd).
Do đó :
2
6
1
3
AB
CD
1 . ĐOẠN THẲNG TỈ LỆ
1 . ĐOẠN THẲNG TỈ LỆ
Tỉ số của hai đoạn thẳng
Đo độ dài các đoạn thẳng, ta
được: AB = 3 cm; CD = 9 cm.
D
C
B
A
N
M
Hình 4.2
Khi đó :
Cho các đoạn thẳng như Hình 4.2 .
Dùng thước thẳng, đo độ dài hai đoạn thẳng AB và CD (đơn
vị: cm) rồi dùng kết quả vừa đo để tính tỉ số
3
9
1
3
AB
CD
1 . ĐOẠN THẲNG TỈ LỆ
1 . ĐOẠN THẲNG TỈ LỆ
Tỉ số của hai đoạn thẳng
Tỉ số tìm được ở Hoạt động 1
và Hoạt động 2 bằng nhau và
đều bằng
D
C
B
A
N
M
Hình 4.2
Cho các đoạn thẳng như Hình 4.2 .
So sánh hai tỉ số tìm được trong hai hoạt động 1 và 2.
a) Tỉ số của các đoạn thẳng được tính như sau:
1 . ĐOẠN THẲNG TỈ LỆ
1 . ĐOẠN THẲNG TỈ LỆ
Tỉ số của hai đoạn thẳng
b) Đổi 10 dm = 100 cm.
Tỉ số của các đoạn thẳng được tính như sau:
3
9
1
3
MN
PQ
1
9
;
3
3PQ
MN
25
10
1
40
EF
HK
100
2
4
1
;
5
HK
EF
•
Cho bốn đoạn thẳng AB, CD, A’B’, C’D’ (H 4.3)
Ta thấy :
Ta có tỉ lệ thức :
1 . ĐOẠN THẲNG TỈ LỆ
1 . ĐOẠN THẲNG TỈ LỆ
Đoạn thẳng tỉ lệ .
Khi đó, ta nói AB và CD tỉ lệ với A’B’ và C’D’.
Hình 4.3
2
3
AB
CD
' '
' '
AB A B
CD C D
' ' 4 2
;
' ' 6 3
A B
C D
a) Từ hình vẽ ta thấy :
1 . ĐOẠN THẲNG TỈ LỆ
1 . ĐOẠN THẲNG TỈ LỆ
Đoạn thẳng tỉ lệ .
Hình 4.4
Do đó :
b) Từ hình vẽ ta thấy :
Do đó :
3
' 4
6
2AB
AB
' 4
;
6
2
3
AC
AC
' 'AB AC
AB AC
' 4
' 2
2
1
AB
B B
' 4
;
' 2
2
1
AC
C C
' '
' '
AB AC
B B C C
c) Từ hình vẽ ta thấy :
1 . ĐOẠN THẲNG TỈ LỆ
1 . ĐOẠN THẲNG TỈ LỆ
Đoạn thẳng tỉ lệ .
Hình 4.4
Do đó :
Cho tam giác ABC và một điểm B’ nằm trên cạnh AB. Qua điểm B’, ta
vẽ một đường thẳng song song với BC, cắt AC tại C’ (H.4.4).
2
a) và b) và c) và
D
o
A
n
h
T
u
a
n
3
' 2
6
1B B
AB
' 2
;
6
1
3
C C
AC
' 'B B C C
AB AC
2 . ĐỊNH LÍ THALES TRONG TAM GIÁC
2 . ĐỊNH LÍ THALES TRONG TAM GIÁC
Định lí Thalès trong tam giác.
ABC , B’C’ // BC
GT
KL
C'
B'
C
B
A
' ' ' ' ' '
; ;
' '
AB AC AB AC B B C C
AB AC B B C C AB AC
Xét tam giác DEF có MN // EF nên theo định lí
Thales , ta có :
Hay
2 . ĐỊNH LÍ THALES TRONG TAM GIÁC
2 . ĐỊNH LÍ THALES TRONG TAM GIÁC
Định lí Thalès trong tam giác.
Suy ra
AM DN
ME NF
2
4 5
x
2.5
4
2,5x
a) Áp dụng định lí Thalès vào ∆ABC, ta có:
b) Ta có: PQ = PF + QF = 5 + 3,5 = 8,5 (đvđd).
2 . ĐỊNH LÍ THALES TRONG TAM GIÁC
2 . ĐỊNH LÍ THALES TRONG TAM GIÁC
Định lí Thalès trong tam giác.
hay
Suy ra
(đvđd)
Áp dụng định lí Thalès vào ∆PHQ, ta có:
hay
Suy ra
(đvđd)
AM AN
BM CN
6.5 4
2x
6,5.2
, 2
4
3 5x
PE PF
PH PQ
4 5
8,5y
4.8,5
6,
5
8y
2 . ĐỊNH LÍ THALES TRONG TAM GIÁC
2 . ĐỊNH LÍ THALES TRONG TAM GIÁC
Định lí Thalès đảo.
Ta có :
Cho ∆ABC có AB = 6 cm, AC = 9 cm. Trên cạnh AB lấy điểm B’, trên cạnh AC
lấy điểm C’ sao cho AB’ = 4 cm, AC’ = 6 cm
+ So sánh các tỉ số và
+ Vẽ đường thẳng a đi qua B’ và song song với BC, đường thẳng a cắt AC tại C”. Tính độ
dài đoạn thẳng AC”
+ Nhận xét gì về hai điểm C’, C” và hai đường thẳng B’C’ , BC ?
C'
C"
B'
C
B
A
Hình 4.7
Do đó :
Đường thẳng a đi qua B’ và song song với BC, đường thẳng
qua a cắt AC tại điểm C’’ nên B’C’’ // BC.
Áp dụng định lí Thalès vào ∆ABC, ta có:
hay
3
' 4
6
2AB
AB
' 6
;
9
2
3
AC
AC
' 'AB AC
AB AC
' "AB AC
AB AC
4 "
6 9
AC
2 . ĐỊNH LÍ THALES TRONG TAM GIÁC
2 . ĐỊNH LÍ THALES TRONG TAM GIÁC
Định lí Thalès đảo.
Cho ∆ABC có AB = 6 cm, AC = 9 cm. Trên cạnh AB lấy điểm B’, trên cạnh AC
lấy điểm C’ sao cho AB’ = 4 cm, AC’ = 6 cm
+ So sánh các tỉ số và
+ Vẽ đường thẳng a đi qua B’ và song song với BC, đường thẳng a cắt AC tại C”. Tính độ
dài đoạn thẳng AC”
+ Nhận xét gì về hai điểm C’, C” và hai đường thẳng B’C’ , BC ?
C'
C"
B'
C
B
A
Hình 4.7
Suy ra :
Trên cạnh AC lấy điểm C’ sao cho AC’ = 6 cm.
Đường thẳng a đi qua B’ và song song với BC, đường thẳng
qua a cắt AC tại điểm C’’ nên điểm C’’ nằm trên cạnh AC sao
cho AC’’ = 6 cm.
Do đó, hai điểm C’, C’’ trùng nhau.
Vì hai điểm C’, C’’ trùng nhau mà B’C’’ // BC nên B’C’ // BC.
4.9
" ( )
6
6AC cm
2 . ĐỊNH LÍ THALES TRONG TAM GIÁC
2 . ĐỊNH LÍ THALES TRONG TAM GIÁC
Định lí Thalès đảo.
ABC , ;
GT
KL
C'
B'
C
B
A
' '/ /B C BC
Trong tam giác DEF, ta có :
2 . ĐỊNH LÍ THALES TRONG TAM GIÁC
2 . ĐỊNH LÍ THALES TRONG TAM GIÁC
Định lí Thales đảo.
Vì nên MN // EF (Theo định lí đảo Thales)
Vì
2
4
1
2
DM
ME
2,5 1
2
;
5
DN
NF
1
2
DM DN
ME NF
Hai cạnh AC và BD thuộc hai bờ của con sông
nên AC // BD, áp dụng định lí Thalès, ta có:
2 . ĐỊNH LÍ THALES TRONG TAM GIÁC
2 . ĐỊNH LÍ THALES TRONG TAM GIÁC
hay
Suy ra
Vậy khoảng cách giữa C và D bằng 375 m.
AE CE
AB CD
400 500
300 CD
300.500
( )
400
375CD m
CÒN TIẾP …
CÒN TIẾP …
Để có cả bộ Giáo án Pp Toán 8 – KNTT , xin liên hệ :
Đỗ Anh Tuấn - Zalo : 0918.790.615
Thầy (cô) có thể tham khảo trước nội dung các bài giảng tại đây :
https://sites.google.com/view/giaoandientu-doanhtuan
(copy đường link và dán vào trình duyệt )
( Bản full sẽ có hiệu ứng trình chiếu từng bước một
và không có tên người soạn )
( Bản full sẽ có hiệu ứng trình chiếu từng bước một
và không có tên người soạn )
( Bản full sẽ có hiệu ứng trình chiếu từng bước một và
không có tên người soạn )
( Bản full sẽ có hiệu ứng trình chiếu từng bước một
và không có tên người soạn )
( Bản full sẽ có hiệu ứng trình chiếu từng bước một
và không có tên người soạn )

Tài liệu khác của Toán 8

Preview text:

Cây cầu AB bắc qua một con sông có chiều
rộng 300 m. Để đo khoảng cách giữa hai điểm C
và D trên hai bờ con sông, người ta chọn một
điểm E trên đường thẳng AB sao cho ba điểm E,
C, D thẳng hàng. Trên mặt đất, người ta đo được AE = 400 m, EC = 500 m.
Theo em, người ta tính khoảng cách
giữa C và D như thế nào?
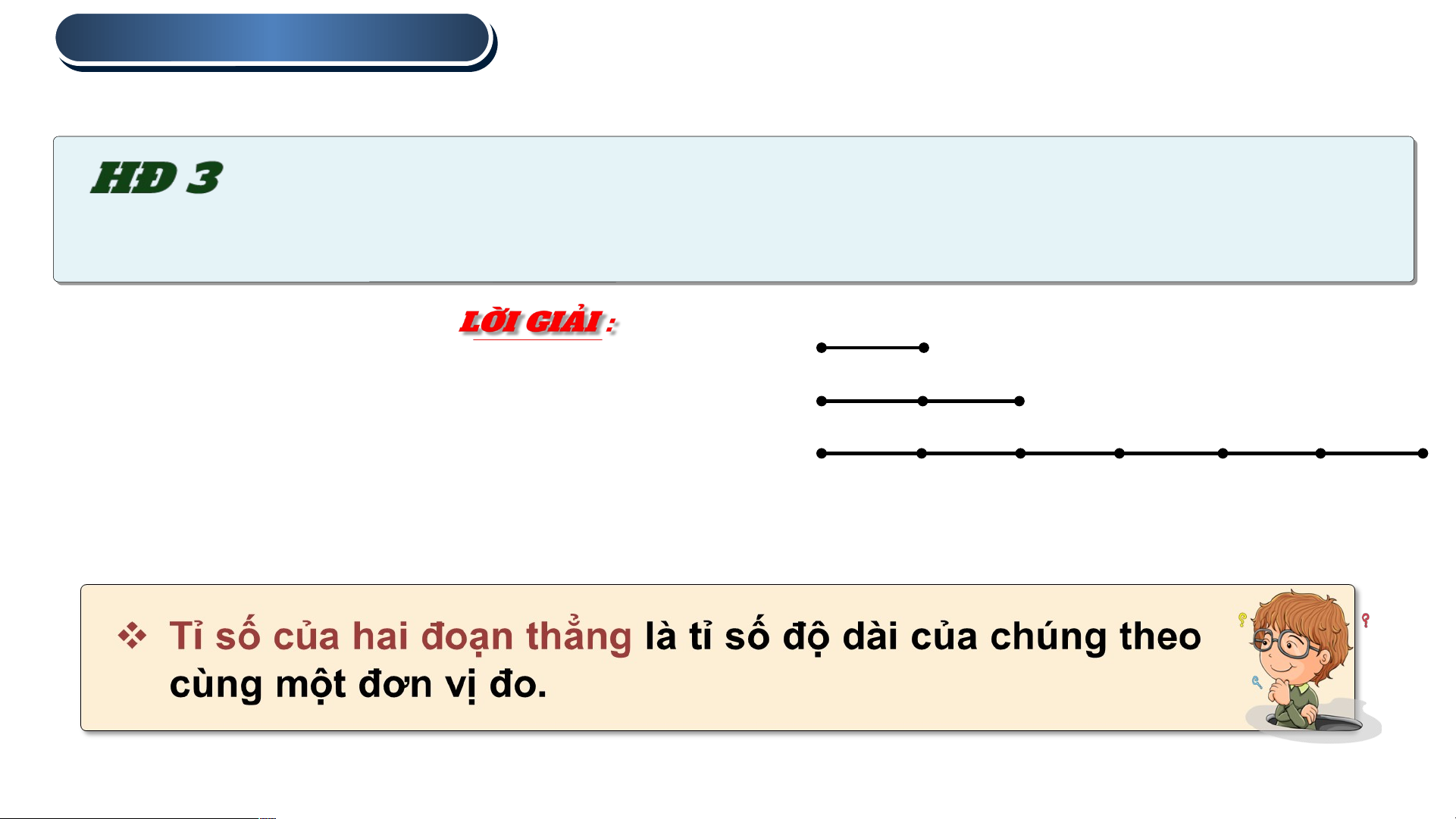
1 . ĐOẠN THẲNG TỈ LỆ LỆ
Tỉ số của hai đoạn thẳng
Cho các đoạn thẳng như Hình 4.2 .
Hãy tìm độ dài của hai đoạn thẳng AB và CD nếu chọn đoạn
MN làm đơn vị độ dài. Với các độ dài đó hãy tính tỉ số M N
Chọn đoạn MN làm đơn vị độ dài A B thì MN = 1 (đvđd). C D
Khi đó, AB = 2 (đvđd) Hình 4.2 CD = 6 (đvđd). AB 2 1 Do đó :   CD 6 3
1 . ĐOẠN THẲNG TỈ LỆ LỆ
Tỉ số của hai đoạn thẳng
Cho các đoạn thẳng như Hình 4.2 .
Dùng thước thẳng, đo độ dài hai đoạn thẳng AB và CD (đơn
vị: cm) rồi dùng kết quả vừa đo để tính tỉ số M N
Đo độ dài các đoạn thẳng, ta A B
được: AB = 3 cm; CD = 9 cm. C D AB 3 1 Hình 4.2 Khi đó :   CD 9 3
1 . ĐOẠN THẲNG TỈ LỆ LỆ
Tỉ số của hai đoạn thẳng
Cho các đoạn thẳng như Hình 4.2 .
So sánh hai tỉ số tìm được trong hai hoạt động 1 và 2. M N
Tỉ số tìm được ở Hoạt động 1 A B
và Hoạt động 2 bằng nhau và C D đều bằng Hình 4.2
1 . ĐOẠN THẲNG TỈ LỆ LỆ
Tỉ số của hai đoạn thẳng
a) Tỉ số của các đoạn thẳng được tính như sau: MN 3 1 PQ 9 3   ;   PQ 9 3 MN 3 1 b) Đổi 10 dm = 100 cm.
Tỉ số của các đoạn thẳng được tính như sau: EF 25 1 HK 100 4   ;   HK 100 4 EF 25 1
1 . ĐOẠN THẲNG TỈ LỆ LỆ
Đoạn thẳng tỉ lệ . •
Cho bốn đoạn thẳng AB, CD, A’B’, C’D’ (H 4.3) Ta thấy : AB 2 A'B' 4 2  ;   CD 3 C 'D' 6 3 AB A'B'
Ta có tỉ lệ thức :CD C 'D' Hình 4.3
Khi đó, ta nói AB và CD tỉ lệ với A’B’ và C’D’.
1 . ĐOẠN THẲNG TỈ LỆ LỆ
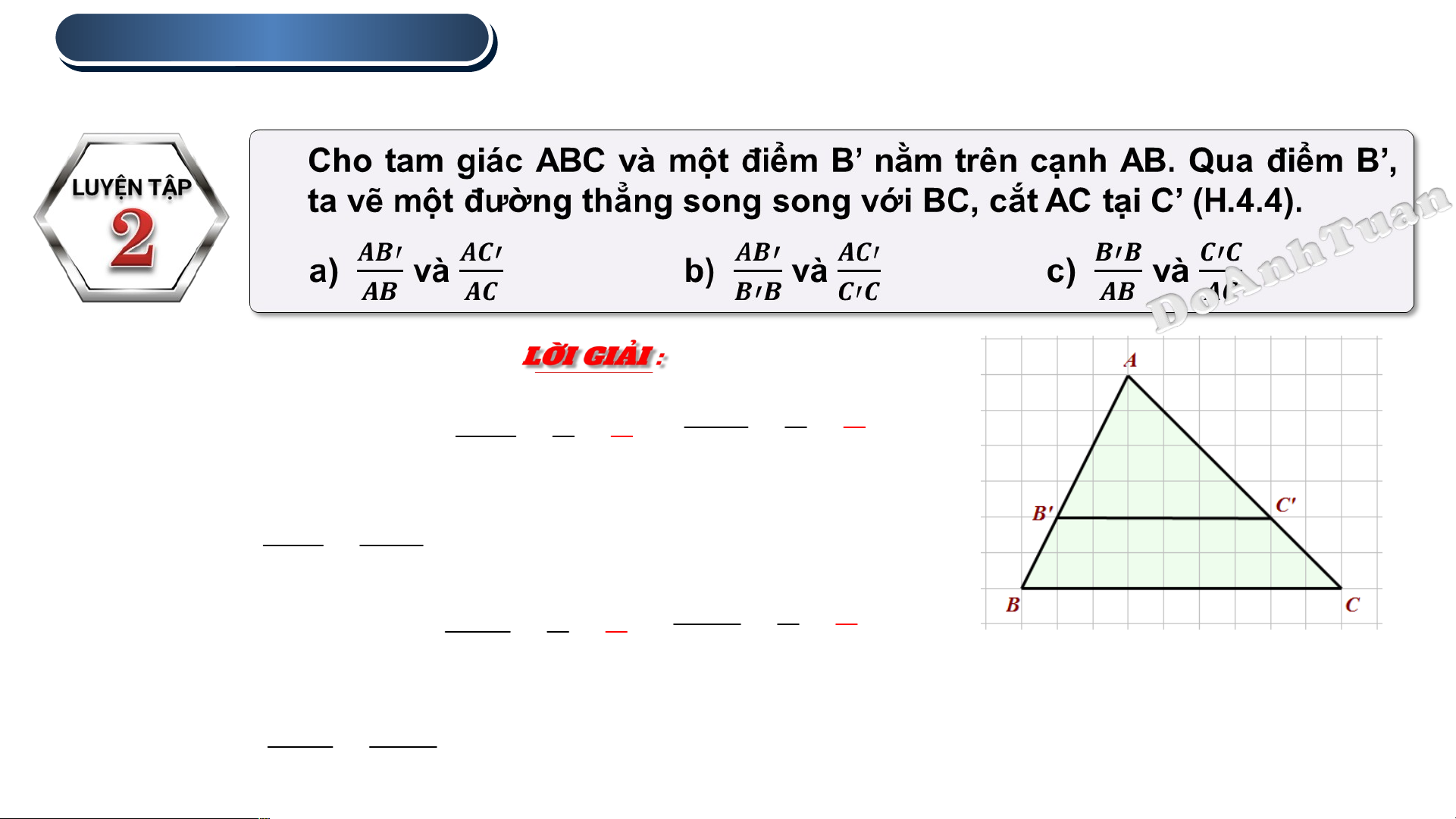
Đoạn thẳng tỉ lệ . AC ' 4 2
a) Từ hình vẽ ta thấy : AB ' 4 2   ;   AB 6 3 AC 6 3 Do đó : AB ' AC '  AB
AC AB' 4 2 AC' 4 2
b) Từ hình vẽ ta thấy :   ;   B ' B 2 1 C 'C 2 1 Hình 4.4 Do đó : AB ' AC '  B ' B C 'C
1 . ĐOẠN THẲNG TỈ LỆ LỆ
Đoạn thẳng tỉ lệ .
Cho tam giác ABC và một điểm B’ nằm trên cạnh AB. Qua điểm B’, ta
vẽ một đường thẳng song song với BC, cắt AC tại C’ (H.4.4). 2 a) và b) và c) và DoAnhTuan C 'C 2 1
c) Từ hình vẽ ta thấy : B ' B 2 1   ;   AB 6 3 AC 6 3
Do đó : B ' B C 'CAB AC Hình 4.4 2 . ĐỊNH LÍ LÍ TH TH ALE LE S TR TR ONG TAM GIÁC
Định lí Thalès trong tam giác. A
GT ABC , B’C’ // BC B' C' AB ' AC ' AB '
AC ' B ' B C 'C KL  ;  ;  AB AC B ' B C 'C AB AC B C 2 . ĐỊNH LÍ LÍ TH TH ALE LE S TR TR ONG TAM GIÁC
Định lí Thalès trong tam giác.
Xét tam giác DEF có MN // EF nên theo định lí Thales , ta có : AM DNME NF 2 x 2.5 Hay Suy ra x 2,5 4 5   4 2 . ĐỊNH LÍ LÍ TH TH ALE LE S TR TR ONG TAM GIÁC
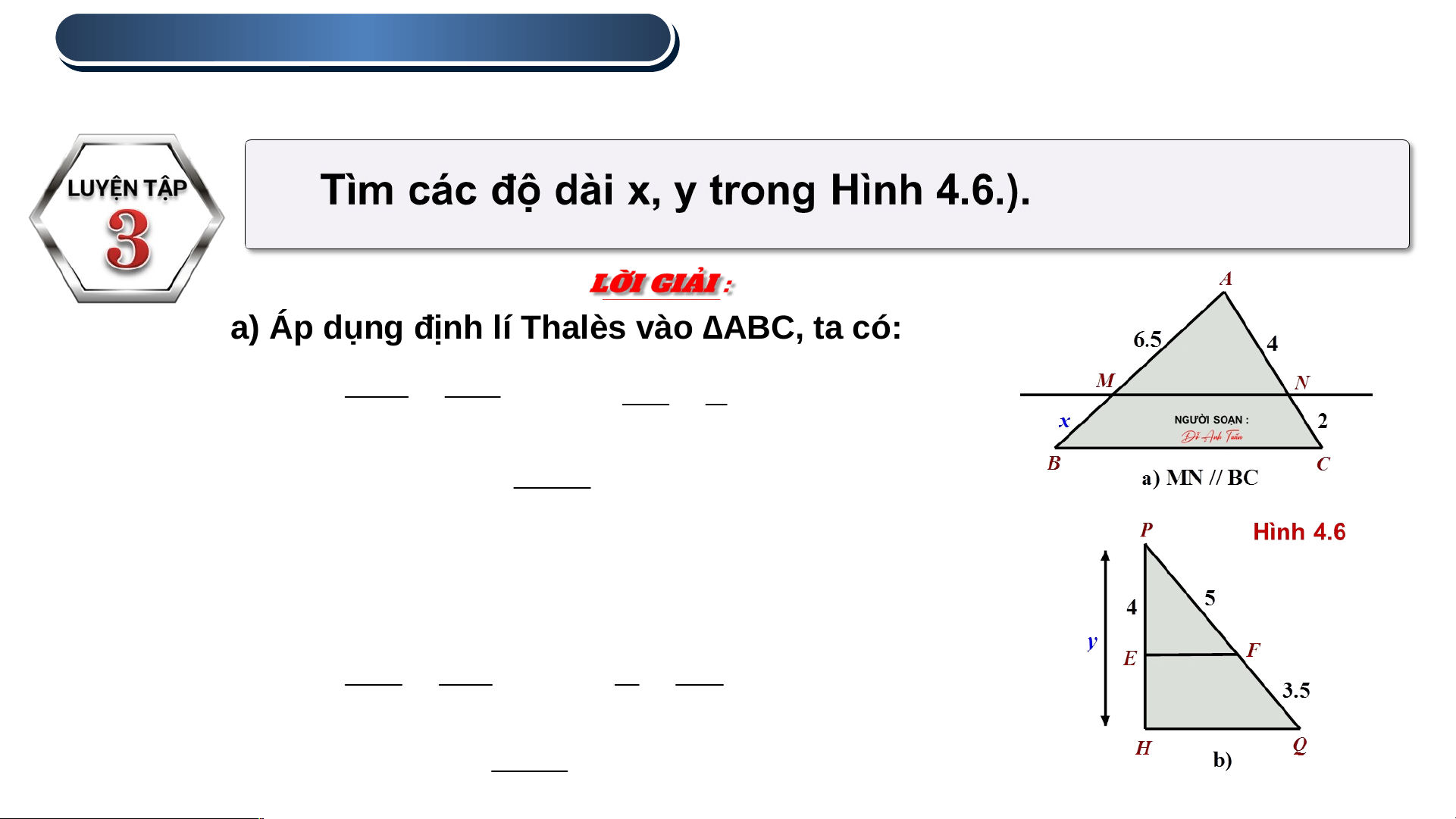
Định lí Thalès trong tam giác.
a) Áp dụng định lí Thalès vào ∆ABC, ta có: AM AN 6.5 4  hay BM CNx 2 6,5.2 Suy ra x   , 3 25 (đvđd) 4
b) Ta có: PQ = PF + QF = 5 + 3,5 = 8,5 (đvđd).
Áp dụng định lí Thalès vào ∆PHQ, ta có: PE PF 4 5  hayPH PQ y 8,5 4.8,5 Suy ra y  6  ,8 (đvđd) 5 2 . ĐỊNH LÍ LÍ TH TH ALE LE S TR TR ONG TAM GIÁC
Định lí Thalès đảo.
Cho ∆ABC có AB = 6 cm, AC = 9 cm. Trên cạnh AB lấy điểm B’, trên cạnh AC
lấy điểm C’ sao cho AB’ = 4 cm, AC’ = 6 cm
+ So sánh các tỉ số và
+ Vẽ đường thẳng a đi qua B’ và song song với BC, đường thẳng a cắt AC tại C”. Tính độ dài đoạn thẳng AC”
+ Nhận xét gì về hai điểm C’, C” và hai đường thẳng B’C’ , BC ? A AB ' 4 2 AC ' 6 2  Ta có :   ;   AB 6 3 AC 9 3 a B' C" AB ' AC ' C' Do đó :AB AC B C
Đường thẳng a đi qua B’ và song song với BC, đường thẳng Hình 4.7
qua a cắt AC tại điểm C’’ nên B’C’’ // BC. AB ' AC " 4 AC "
Áp dụng định lí Thalès vào ∆ABC, ta có:hayAB AC 6 9 2 . ĐỊNH LÍ LÍ TH TH ALE LE S TR TR ONG TAM GIÁC
Định lí Thalès đảo.
Cho ∆ABC có AB = 6 cm, AC = 9 cm. Trên cạnh AB lấy điểm B’, trên cạnh AC
lấy điểm C’ sao cho AB’ = 4 cm, AC’ = 6 cm
+ So sánh các tỉ số và
+ Vẽ đường thẳng a đi qua B’ và song song với BC, đường thẳng a cắt AC tại C”. Tính độ dài đoạn thẳng AC”
+ Nhận xét gì về hai điểm C’, C” và hai đường thẳng B’C’ , BC ? A 4.9 Suy ra : AC "  6  (cm) 6
Trên cạnh AC lấy điểm C’ sao cho AC’ = 6 cm. a B' C" C'
Đường thẳng a đi qua B’ và song song với BC, đường thẳng
qua a cắt AC tại điểm C’’ nên điểm C’’ nằm trên cạnh AC sao B C cho AC’’ = 6 cm. Hình 4.7
Do đó, hai điểm C’, C’’ trùng nhau.
Vì hai điểm C’, C’’ trùng nhau mà B’C’’ // BC nên B’C’ // BC. 2 . ĐỊNH LÍ LÍ TH TH ALE LE S TR TR ONG TAM GIÁC
Định lí Thalès đảo. A ABC , ; GT KL B' C'
B 'C '/ /BC B C 2 . ĐỊNH LÍ LÍ TH TH ALE LE S TR TR ONG TAM GIÁC
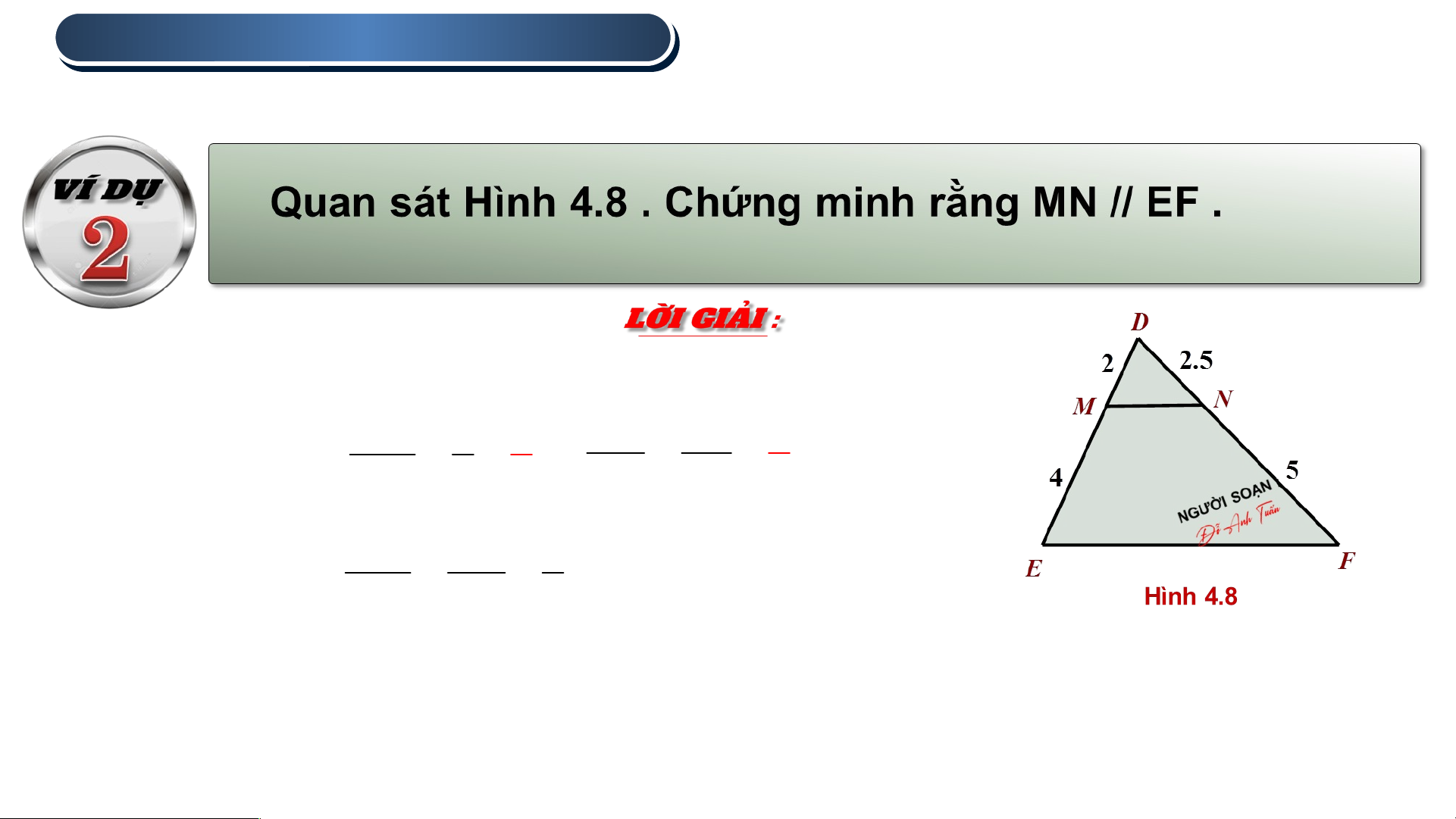
Định lí Thales đảo.
Trong tam giác DEF, ta có : DM 2 1 DN 2,5 1   ;   ME 4 2 NF 5 2 DM DN 1 Vì   ME NF 2
Vì nên MN // EF (Theo định lí đảo Thales) 2 . ĐỊNH LÍ LÍ TH TH ALE LE S TR TR ONG TAM GIÁC
Hai cạnh AC và BD thuộc hai bờ của con sông
nên AC // BD, áp dụng định lí Thalès, ta có: AE CE 400 500  hayAB CD 300 CD 300.500 Suy ra CD  37 ( 5 ) m 400
Vậy khoảng cách giữa C và D bằng 375 m. CÒN TIẾP …
Để có cả bộ Giáo án Pp Toán 8 – KNTT , xin liên hệ :
Đỗ Anh Tuấn - Zalo : 0918.790.615
Thầy (cô) có thể tham khảo trước nội dung các bài giảng tại đây :
https://sites.google.com/view/giaoandientu-doanhtuan
 (copy đường link và dán vào trình duyệt )
( Bản full sẽ có hiệu ứng trình chiếu từng bước một
và không có tên người soạn )
( Bản full sẽ có hiệu ứng trình chiếu từng bước một
và không có tên người soạn )
( Bản full sẽ có hiệu ứng trình chiếu từng bước một và
không có tên người soạn )
( Bản full sẽ có hiệu ứng trình chiếu từng bước một
và không có tên người soạn )
( Bản full sẽ có hiệu ứng trình chiếu từng bước một
và không có tên người soạn )
Document Outline

  • Slide 1
  • Slide 2
  • Slide 3
  • Slide 4
  • Slide 5
  • Slide 6
  • Slide 7
  • Slide 8
  • Slide 9
  • Slide 10
  • Slide 11
  • Slide 12
  • Slide 13
  • Slide 14
  • Slide 15
  • Slide 16
  • Slide 17
  • Slide 18
  • Slide 19
  • Slide 20
  • Slide 21
  • Slide 22
  • Slide 23
  • Slide 24
  • Slide 25
  • Slide 26
  • Slide 27

Tài liệu liên quan: