THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU
1. Giáo viên: Máy tính, bảng phụ, SGK, phiếu học tập.
2. Học sinh: SGK, bảng nhóm. HĐ H HĐ H NH N Ó H M HĐ H CÁ C N Á H N ÂN Â CẶ C P Ặ Đ P Ô Đ I Ô 01 MỞ ĐẦU
Em hãy nhắc lại các bước
trừ hai đa thức một biến theo hàng ngang.
- Bước 1. Thu gọn mỗi đa thức và sắp xếp đa thức đó theo số mũ giảm dần của biến;
- Bước 2. Viết hiệu đa thức theo hàng ngang, trong đó đa thức được đặt trong dấu ngoặc;
- Bước 3. Bỏ dấu ngoặc và đổi dấu mỗi đơn thức trong dạng thu gọn của ,
nhóm các đơn thức có cùng số mũ của biến với nhau;
- Bước 4. Thực hiện phép tính trong từng nhóm ta được hiệu cần tìm.
Bài 2: CÁC PHÉP TÍNH VỚI ĐA THỨC NHIỀU BIẾN Tiế T t 1: Cộng h ai a đa t hức hứ n hiều ề b iến. Tiế T t 2: Tr T ừ r ừ h ai a đa t hức hứ n hiều ề b iến. Tiế T t 3: Nh N ân h â ai a đ a t a hức hứ n c hiều bi ến. Tiế T t 4 : : Chia đa a t hức ứ c c h c o đơn o đơ t hức hứ . S E T O N C M ÁCA T
PHÉP TÍNH VỚI ĐA THỨC H NHIỀU BIẾN
MỤC TIÊU CẦN ĐẠT 1 - Kiến n thức
th : Thực hiệ
i n được phép trừ đa thức nhiề i u biến 2
- Năng lực: Tự học, giao tiế ti p và hợp tá t c, tư duy và lậ l p lu
l ận toán học, sử dụng công cụ và phương tiện học T o T án. 3 - Phẩ h m chấ
h t: Chăm chỉ, tru tr ng thực, trách nhiệm. 02 HÌNH THÀNH KIẾN THỨC
II. Trừ hai đa thức nhiều biến Cho hai đa thức và .
a) Viết hiệu theo hàng ngang, trong đó đa
thức được đặt trong dấu ngoặc. .
b) Sau khi bỏ dấu ngoặc và đổi dấu mỗi đơn
thức của đa thức , nhóm các đơn thức đồng dạng với nhau.
c) Tính hiệu bằng cách thực hiện phép tính trong từng nhóm.
§2. CÁC PHÉP TÍNH VỚI ĐA THỨC NHIỀU BIẾN ( tiết 2)
II. Trừ hai đa thức nhiều biến Ta có: Viết lại đa thức
¿ 𝑥2+ 2 𝑥 𝑦 + 𝑦 2− 𝑥2+2 𝑥 𝑦 − 𝑦2 Phá ngoặc
¿ ( 𝑥2− 𝑥2 )+ ( 2 𝑥 𝑦 +2 𝑥 𝑦 ) + ( 𝑦2 − 𝑦2 N
) hóm đơn thức đồng dạng ¿ 4 𝑥𝑦 Thực hiện phép tính Nhận xét
- Viết hiệu theo hàng ngang, trong đó đa thức được đặt trong dấu
Em hãy nêu các bước thực hiện ngoặc.
phép trừ hai đa thức nhiều biến.
- Sau khi bỏ dấu ngoặc và đổi dấu mỗi đơn thức của đa thức , nhóm
các đơn thức đồng dạng với nhau.
- Thực hiện phép tính trong từng nhóm, ta được hiệu cần tìm.
Ví dụ 3: Cho ba đa thức: , và . Tính: a) b) Bài giải: a)
¿ 𝑥2−2 𝑥𝑦 + 𝑦 2− 2 𝑥2+ 𝑦2
¿ − 𝑥2− 2 𝑥𝑦 +2 𝑦2 b)
¿ ( 𝑥2− 𝑥2)+ (− 2 𝑥𝑦 + 3 𝑥𝑦 )+ 𝑦2
¿ 𝑥𝑦 + 𝑦 2 Cho ba đa thức , và . Tính: a) b) Bài giải: a)
¿ 2 𝑥2 − 𝑦 2− 𝑥2+3 𝑥𝑦
¿ 𝑥2+ 3 𝑥𝑦 − 𝑦2 b)
¿ ( 𝑥2 + 𝑥2 )+ ( 3 𝑥𝑦 − 2 𝑥𝑦 ) +( − 𝑦 2+ 𝑦2)
¿ 2 𝑥2+ 𝑥𝑦 03 LUYỆN TẬP
Bài 1: Cho đa thức và . Tính: a) b) Bài giải: a)
¿ 𝑥2−3 𝑥𝑦 + 8 𝑦 b)
¿ 𝑥2+ 𝑥𝑦 −5 𝑦 − 4 𝑥2− 𝑦
¿ −3 𝑥2+ 𝑥𝑦 − 6 𝑦
Bài 1: Cho đa thức , và . Tính: Nhóm 1+2: Nhóm 3+4: c) . d) . Bài giải: c) d) .
¿ ( 𝑥2− 3 𝑥𝑦 + 8 𝑦 )−( 4 𝑥2+ 𝑦 ) )
¿ ( 𝑥2− 3 𝑥𝑦 + 8 𝑦 )− 4 𝑥2 − 𝑦 )
¿ −3 𝑥2− 3 𝑥𝑦 +7 𝑦
¿ −5 𝑥2+ 3 𝑥𝑦 − 9 𝑦
Bài 2: Cho hai đa thức và . Tìm đa thức biết Bài giải: Ta có:
¿ (2 𝑥+ 𝑥𝑦 + 3 𝑦2) − ( 𝑥 −5 𝑥𝑦 − 𝑦 2)
¿ 2 𝑥+ 𝑥𝑦 +3 𝑦2− 𝑥+5 𝑥𝑦 + 𝑦2
¿ 𝑥+ 6 𝑥𝑦+ 4 𝑦2 04 VẬN DỤNG
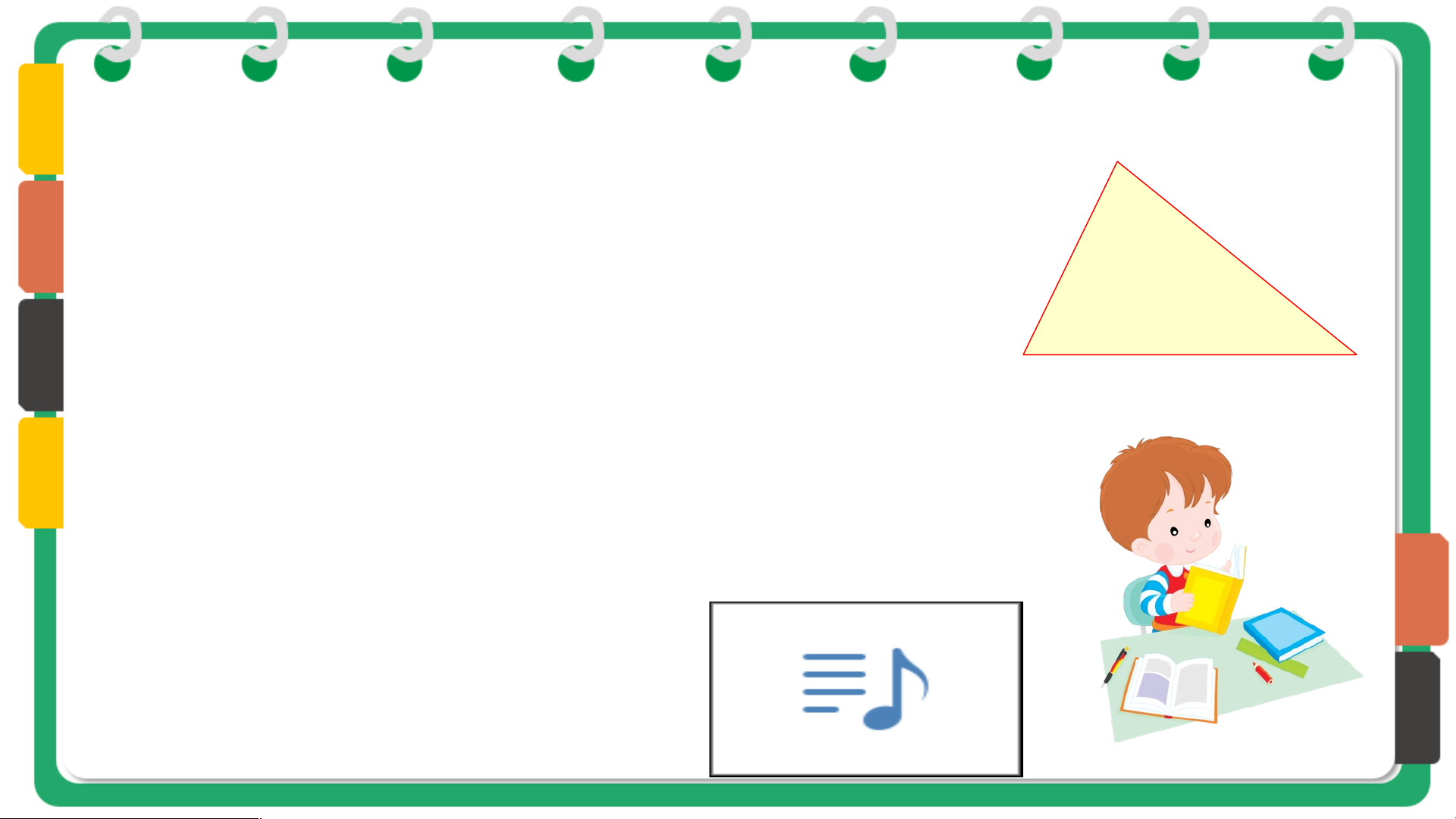
Bài 3: Tìm độ dài cạnh còn lại của tam giác 2 2 𝑦 𝑥+
ở hình bên, biết rằng tam giác có chu vi bằng − 𝑦 2 . 𝑥 Bài giải:
Độ dài cạnh còn lại của tam giác là:
2 𝑥 +3 𝑦2− ( 𝑥 − 𝑦2+2 𝑥+ 𝑦2)
¿ 2 𝑥+3 𝑦2− 3 𝑥 . TRÒ CHƠI AI LÀ TRIỆU PHÚ 01:00 00:59 00:58 00:57 00:56 00:55 00:54 00:53 00:52 00:51 00:50 00:49 00:48 00:47 00:46 00:45 00:44 00:43 00:42 00:41 00:40 00:39 00:38 00:37 00:36 00:35 00:34 00:33 00:32 00:31 00:30 00:29 00:28 00:27 00:26 00:25 00:24 00:23 00:22 00:21 00:20 00:19 00:18 00:17 00:16 00:15 00:14 00:13 00:12 00:11 00:10 00:09 00:08 00:07 00:06 00:05 00:04 00:03 00:02 00:01 00:
Câu hỏi 1: Tính hiệu của đa thức biết và .  A.  B.  C.  D. 01:00 00:59 00:58 00:57 00:56 00:55 00:54 00:53 00:52 00:51 00:50 00:49 00:48 00:47 00:46 00:45 00:44 00:43 00:42 00:41 00:40 00:39 00:38 00:37 00:36 00:35 00:34 00:33 00:32 00:31 00:30 00:29 00:28 00:27 00:26 00:25 00:24 00:23 00:22 00:21 00:20 00:19 00:18 00:17 00:16 00:15 00:14 00:13 00:12 00:11 00:10 00:09 00:08 00:07 00:06 00:05 00:04 00:03 00:02 00:01 00:
Câu hỏi 2: Đa thức là hiệu của hai đa thức nào dưới đây?  A.  B.  C.  D. 01:00 00:59 00:58 00:57 00:56 00:55 00:54 00:53 00:52 00:51 00:50 00:49 00:48 00:47 00:46 00:45 00:44 00:43 00:42 00:41 00:40 00:39 00:38 00:37 00:36 00:35 00:34 00:33 00:32 00:31 00:30 00:29 00:28 00:27 00:26 00:25 00:24 00:23 00:22 00:21 00:20 00:19 00:18 00:17 00:16 00:15 00:14 00:13 00:12 00:11 00:10 00:09 00:08 00:07 00:06 00:05 00:04 00:03 00:02 00:01 00:
Câu hỏi 3: Cho hai đa thức và . Tìm đa thức biết  A.  B.  C.  D. 01:00 00:59 00:58 00:57 00:56 00:55 00:54 00:53 00:52 00:51 00:50 00:49 00:48 00:47 00:46 00:45 00:44 00:43 00:42 00:41 00:40 00:39 00:38 00:37 00:36 00:35 00:34 00:33 00:32 00:31 00:30 00:29 00:28 00:27 00:26 00:25 00:24 00:23 00:22 00:21 00:20 00:19 00:18 00:17 00:16 00:15 00:14 00:13 00:12 00:11 00:10 00:09 00:08 00:07 00:06 00:05 00:04 00:03 00:02 00:01 00:
Câu hỏi 4: Cho đa thức , và . Tính  A.  B.  C.  D. 1
Xem lại các dạng bài tập đã chữa. HƯỚNG DẪN VỀ NHÀ 2 Làm bài 4a SGK trang 17 và phiếu bài tập.
3 Chuẩn bị bài mới: đọc trước mục III. NHÂN HAI ĐA THỨC NHIỀU BIẾN.
Document Outline

• Slide 1
• Slide 2
• Slide 3
• Slide 4
• Slide 5
• Slide 6
• Slide 7
• Slide 8
• Slide 9
• Slide 10
• Slide 11
• Slide 12
• Slide 13
• Slide 14
• Slide 15
• Slide 16
• Slide 17
• Slide 18
• Slide 19
• Slide 20
• Slide 21
• Slide 22
• Slide 23
• Slide 24