THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU GIÁO HỌC VIÊN SINH  SGK  SGK  Kế hoạch bài dạy  Thước thẳng  Thước thẳng  Giấy  Máy tính, máy chiếu  Bảng nhóm  Phiếu bài tập CHÚ THÍCH HĐ: HĐ: HĐ: CÁ NHÂN CẶP ĐÔI NHÓM 01 KHỞI ĐỘNG TRÒ CHƠI RÒ CHƠI HỘP Ộ Q P U Q À U BÍ Ẩ N
Trong mỗi hộp quà ẩn chứa
một số điểm bí ấn. Các em
hãy trả lời đúng các câu hỏi
để nhận về phần quà cho mình nhé. 50 điểm 60 điểm 90 điểm 40 điểm 90 điểm 70 điểm START 1  1
Giá trị của biểu thức  x 3 2 y tại x  ; y   4 là: 12 2 2 9 3 6 A. 1 C. 2 Hết Giờ B. 1 CH C Ú H C Ú C D. 2 MỪN MỪ G N START Tr T o r ng n các biể bi u thức sau, u biể b u thức nà n o là đơn thức t ? 12 9 3 6 CH C Ú H C Ú C A. B. MỪN MỪ G N Hết Giờ C. D. . . START 1 Kết quả t qu của phé ph p tính p tín  x 2 y  2 2 x y là l : 12 2 9 3 6 5 3 4 2 A. 2  x y B. x y Hết Giờ 2 2 3 2 CH C Ú H C Ú C 3 C. x y D. 4 x y 2 MỪN MỪ G N 2 START Xác địn đ h đơ ịn n n thức t M M để đ 2 2
7xy  M 3xy 12 9 3 6 CH C Ú H C Ú C A. MỪN MỪ G N B. 10xy2 B. 10xy Hết Giờ C. 4xy2 C. 4xy D. 4x2y4 D. 4x2y START Biể i u thức u th nà n o dưới đâ đ y không phả ph i là đa thứ th c? 12 9 3 6 Hết Giờ A. 3x 3 (y – 2) C. D. B. 2x CH C Ú H C Ú C MỪN MỪ G N START Cho h đa thức: 4 3 3 5 4 3 A 2
 x y  9xy  12x  2x y  2023 Bậc của đa thức
th A là: 12 9 3 6 CHÚC A. 5 CHÚC B. 12 Hết Giờ MỪNG MỪN C. 7 D. 4
Ở lớp 7, ta đã học cách thực
hiện phép cộng, phép trừ, phép nhân,
phép chia các đa thức một biến. Vậy
các phép tính với đa thức nhiều biến
được thực hiện như thế nào? 02 HÌNH THÀNH KIẾN THỨC §2. CÁC PHÉP C PH ÉP TÍN H H VỚI ĐA ĐA TH Ứ TH C NHIỀU B IẾN I
CỘNG HAI ĐA THỨC NHIỀU BIẾN
II TRỪ HAI ĐA THỨC NHIỀU BIẾN III
NHÂN HAI ĐA THỨC NHIỀU BIẾN IV
CHIA ĐA THỨC CHO ĐƠN THỨC Mục tiêu 1. Về kiến thức:
– Thực hiện được phép nhân đơn thức với đa thức và phép chia
hết một đơn thức cho một đơn thức.
– Thực hiện được các phép tính: phép cộng, phép trừ, phép nhân
các đa thức nhiều biến trong những trường hợp đơn giản.
– Thực hiện được phép chia hết một đa thức cho một đơn thức
trong những trường hợp đơn giản. Mục tiêu 2. Về năng lực: * Về năng lực chung:
- Năng lực tự học: HS tự hoàn thành được các nhiệm vụ học tập chuẩn bị ở nhà và tại lớp;
- Năng lực giao tiếp và hợp tác: HS phân công được nhiệm vụ trong nhóm,
biết hỗ trợ nhau, trao đổi, thảo luận, thống nhất được ý kiến trong nhóm để hoàn thành nhiệm vụ;
- Năng lực giải quyết vấn đề và sáng tạo: Vận dụng linh hoạt, sáng tạo kiến
thức đã học vào giải quyết các bài toán thực tế. Mục tiêu 2. Về năng lực: * Năng lực đặc thù:
- Thực hiện được các phép tính: Phép cộng các đa thức nhiều biến trong
những trường hợp đơn giản.
- Năng lực giao tiếp toán học: phát biểu các nhận xét về quy tắc thực hiện
các phép tính phép cộng, phép trừ, phép nhân các đa thức
- Năng lực sử dụng công cụ và phương tiện học toán: Sử dụng được các
công cụ, phương tiện học toán để thực hiện những nhiệm vụ học tập toán đơn
giản. Làm quen với máy tính cầm tay, phương tiện công nghệ thông tin hỗ trợ học tập.
- Năng lực tư duy và lập luận toán học, năng lực giải quyết vấn đề toán học,
năng lực mô hình hóa toán học: thực hiện được các thao tác tư duy so sánh,
phân tích, tổng hợp, khái quát hóa, đưa ra cách thực hiện các phép tính với đa
thức nhiều biến hợp lý. Mục tiêu 3. Về phẩm chất:
- Chăm chỉ: thực hiện đầy đủ các hoạt động học tập một cách tự giác, tích cực.
- Trung thực: thật thà, thẳng thắn trong báo cáo kết quả hoạt
động cá nhân và theo nhóm, trong đánh giá và tự đánh giá.
- Trách nhiệm: hoàn thành đầy đủ, có chất lượng các nhiệm vụ học tập.
I. CỘNG HAI ĐA THỨC NHIỀU BIẾN 2 2
HĐ1: Tính tổng của hai đa thức P  x 2  x y  2 2
y và Q x
 – 2xy  y Theo các bước sau:
a) Viết tổng P + Q theo hang ngang;
b) Nhóm các đơn thức đồng dạng với nhau;
c) Tính tổng P + Q bằng cách thực hiện phép tính trong từng nhóm. Lời giải: P  Q  2 2
 x  2xy  y    2 2
x – 2xy  y  2 2 2 2
 x  2xy  y  x – 2xy  y   2 2
x  x    2xy – 2xy   2 2 y  y  2 2  2x  2 y Nhận xét:
Để cộng hai đa thức theo hàng ngang, ta có thể làm như sau:
Viết tổng hai đa thức theo hàng ngang;
Nhóm các đơn thức đồng dạng với nhau;
Thực hiện phép tính theo trong từng nhóm, ta được tổng cần tìm.
Ví dụ 1: Tính tổng của hai đa thức: 3 2 2 3 P x 
 3x y  3xy  y và 3 2 2 3 Q x 
– 3x y  3xy – y Lời giải: P  Q  3 2 2 3
 x  3x y  3xy  y    3 2 2 3
x – 3x y  3xy – y  3 2 2 3 3 2 2 3
 x  3x y  3xy  y  x – 3x y  3xy – y   3 3
x  x   2 2
3x y – 3x y    2 2
3xy  3xy    3 3 y – y  3 2  2x  6xy
Luyện tập 1: Tính tổng của hai đa thức: 3 3
M x  y và 3 3
N x – y Lời giải: M  N  3 3
 x  y    3 3 x – y  3 3 3 3
x  y  x – y  3 3
 x  x    3 3 y – y  3 2  x 03 LUYỆN TẬP LUYỆN T N ẬP
Bài 1. Tính tổng của hai đa thức trong các trường hợp sau:
a) A x  2 y; B x  2y 1 5 2 3 3 2 3
d) A  x y  xy  x y  x 2 2 2 3 2 3 2 b) A 2
 x y  x  xy 1; B x  2xy  2 7 1 3 2 2 3 B  x y  x y  xy 2 2 2 2
c) A x  2yz  z ; B 3
 yz  5x  z 2 2 HĐ nhóm
Tiêu chi đánh giá: Nhóm 1 – a);
+ Đặt đúng phép tính (2 điểm); Nhóm 2 – b);
+ Bỏ ngoặc đúng (2 điểm); Nhóm 3 – c);
+ Sử dụng tính chất giáo hoán, kết hợp - Nhóm đúng Nhóm 4 – d).
các đơn thức đồng dạng (2 điểm).
+ Tính đúng các nhóm (2 điểm);
+ Điểm trình bày (2 điểm) LUYỆN T N ẬP Bài 1. Giải a) A  B 
 x  2 y    x  2y x  2y  x  2y 
 x  x   2y  2y 2  x 2 3 2 3 2 b) A  B (
 2x y  x  xy 1)  (x  2xy  2) 2 3 2 3 2 2
 x y  x  xy 1 x  2xy  2 2 3 3 2 2 2
 x y  ( x  x )  ( xy  2xy )  (1 2) 2 2 2
 x y  xy  1 LUYỆN T N ẬP Bài 1. Giải c) A  B  2 2
 x  2 yz  z    2 2
3yz  5x  z  2 2 2 2
x  2 yz  z  3yz  5x  z  2 2
 x  5x     2yz 3yz   2 2 z  z  2 6  x  yz  1 5   7 1 2 3 3 2 3 3 2 2 3 d) A   B  x y  xy  x y  x  x y  x y  xy  2 2       2 2  1 5 7 1 2 3 3 2 3 3 2 2 3
 x y  xy 
x y  x  x y  x y  xy 2 2 2 2  1 1   5 7 2 2 3 3 3 2 3 2  3  x y 
x y  (xy  xy )   x y  x y  x  2 2       2 2  3 3 2 3 2
 xy  x y  x LUYỆN T N ẬP
Bài 2: Thực hiện phép tính sau: 2 2 2 2
A (x  y  2xy)  (x  2xy  y ) Lời giải: 2 2 2 2
A (x  y  2xy)  (x  2xy  y ) 2 2 2 2
 x  y  2xy  x  2xy  y 2 2 2 2
(x  x )  (y  y )  ( 2xy  2xy) 2 2 2x  2 y LUYỆN T N ẬP
Bài 3: Cho các đa thức: 3 2 2 3 2 M 3
 x  x y  2xy  3; N x y  2xy  2; P 3
 x  2x y  xy  3
Tính: a) M + N + P; b) P + N + M. LUYỆN T N ẬP Bài 3 Lời giải
a) M  N  P  3 2
 3x  x y  2xy  3   2
x y  2xy  2  3 2
3x  2x y  xy  3 3 2 2 3 2 3
 x  x y  2xy  3  x y  2xy  2  3x  2x y  xy  3  3 3
 3x  3x    2 2 2
 x y  x y  2x y    2xy  2xy  xy   3  2  3 3 2 6
 x  2x y  xy  4
b) P  N  M  3 2
 3x  2x y  xy  3   2
x y  2xy  2  3 2
3x  x y  2xy  3 3 2 2 3 2 3
 x  2x y  xy  3  x y  2xy  2  3x  x y  2xy  3  3 3
 3x  3x    2 2 2
 2x y  x y  x y     xy  2xy  2xy   3  2  3 3 2 6
 x  2x y  xy  4
 M  N  P P   N  M LUYỆN T N ẬP Lưu ý:
Trong một tổng nhiều đa thức, ta có thể đổi chỗ các đa thức
tùy ý nhưng tổng không đổi. Ta nói phép cộng các đa thức có tính chất giáo hoán. LUYỆN T N ẬP
Bài 4. Tìm đa thức A, B biết: 2 2 2 2
A  (x  y ) x  2y 3xy  2 2 2
B  (5x  2xyz) 2
 x  2xyz 1 Lời giải: 2 2 2 2 A 2 2
 ( x  y )  x  2 y  3xy  2
B   5x  2xyz 2x  2xyz 1 2 2 2 2 A (
  x  2 y  3xy  2 )  ( x  y ) B  2
 2x  2xyz  1   2 5x  2xyz 2 2 2 2
 x  2 y  3xy  2  x  y 2 2
2x  2xyz  1  5x  2xyz 2 2 2 2 (
  x  x )  (  2 y  y )  3xy  2  2 2
 2x  5x    2xyz  2xyz  1 2
 3 y  3xy  2 2 7  x  1 04 VẬN DỤNG VẬN DỤNG
Bài 5: Bác Huỳnh muốn sơn bề mặt của hai khối gỗ có dạng hình
hộp chữ nhật. Hình hộp chữ nhật thứ nhất có ba kích thước là x
(cm), 2y (cm), z (cm). Hình hộp chữ nhật thứ hai có ba kích thước
là 2x (cm), 2y (cm), 3z (cm). Viết đa thức biểu thị tổng diện tích bề
mặt của hai khối gỗ mà bác Huỳnh cần sơn. Bài 5: Lời giải.
Tổng diện tích các mặt của hình hộp chữ nhật thứ nhất là:
2 x.2y  x.z  2y.z 2 4
 xy  2xz  4 yz (cm )
Tổng diện tích các mặt của hình hộp chữ nhật thứ hai là: 2 [ 2 2 . x 2y  2 . x 3z  2 . y 3z] 8
 xy 12xz 12 yz (cm )
Đa thức biểu thị tổng diện tích bề mặt của hai khối gỗ mà bác Huỳnh cần sơn là:
 4xy  2xz  4yz   8xy 12xz 12yz 4
 xy  2xz  4 yz  8xy 12xz 12 yz 
 4xy  8xy    2xz 12xz    4 yz 12 yz  2 1
 2xy 14xz 16 yz c ( m )
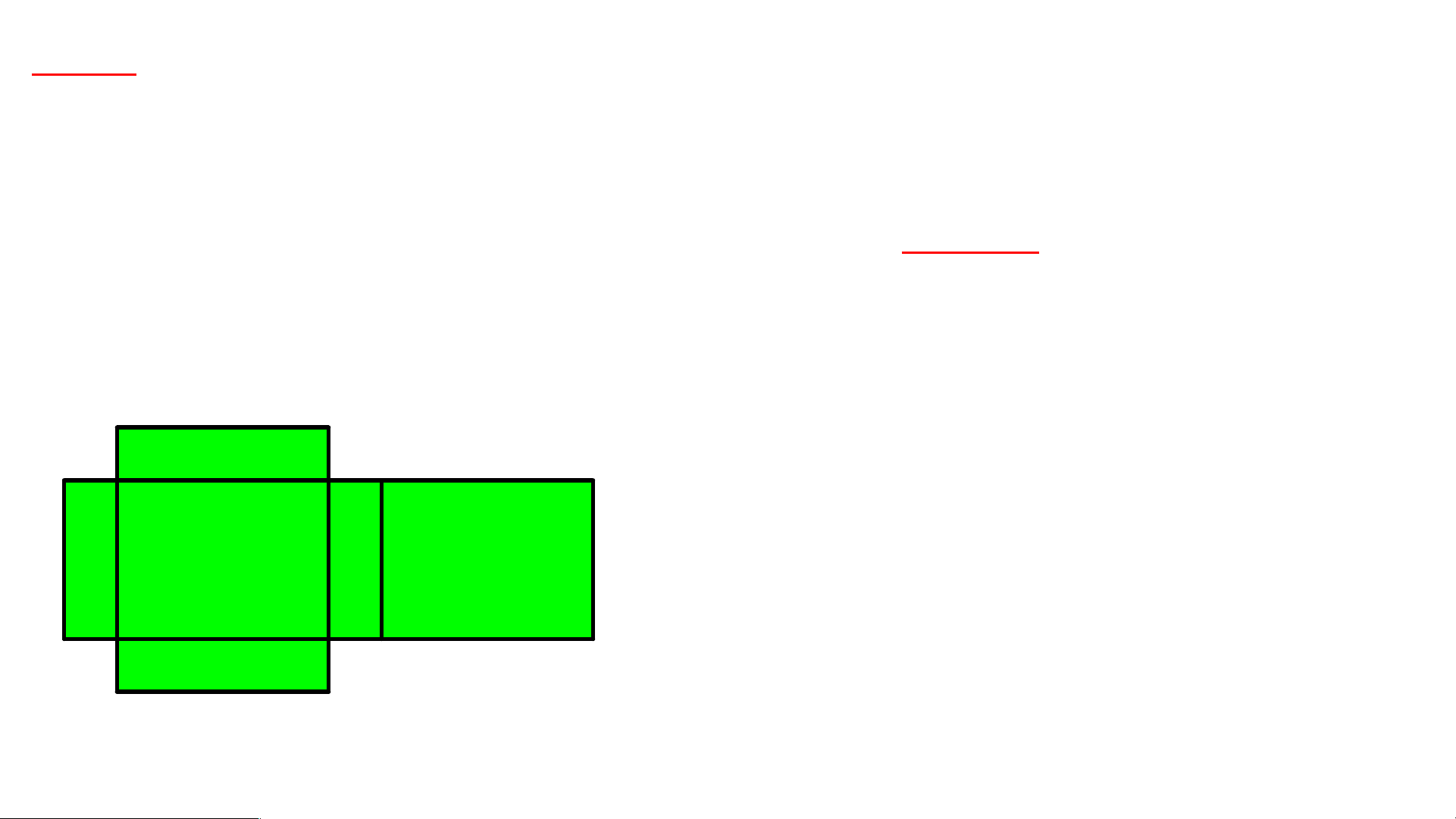
Bài 6. Bạn An cắt một miến bìa có để làm một chiếc hộp hình hộp chữ nhật có ba
kích thước là x; y; z. (cm). Các kích thước và tỉ lệ của hộp phụ thuộc vào các giá
trị của x; y; z. Tính tổng diện tích của các mặt của hình hộp chữ nhật được thể hiện qua hình đó. Lời giải
Tổng diện tích của các mặt của hình hộp chữ nhật là: z
xz  xz  xy  xy  yz  yz x z 2 2
 xz  2xy  2 yz (cm ) y x x HƯ H ỚNG DẪN HỌC HỌ Ở NHÀ
- Ghi nhớ các bước để cộng hai đa thức;
- Xem lại các bài đã chữa trên lớp; - Làm bài tập 7:
Bài 7: Cho các đa thức A, B, C: 2 2 2 2 2 2 2 2 2 2 A 4
 x  3y  5 ; x B 3
 x  2y  2x y ; C  4x  y  2x y  5x
Tính: M, P, Q. Biết:
M A  B  C P  A C  Q  B C 
Document Outline

• Slide 1
• Slide 2
• Slide 3
• Slide 4
• Slide 5
• Slide 6
• Slide 7
• Slide 8
• Slide 9
• Slide 10
• Slide 11
• Slide 12
• Slide 13
• Slide 14
• Slide 15
• Slide 16
• Slide 17
• Slide 18
• Slide 19
• Slide 20
• Slide 21
• Slide 22
• Slide 23
• Slide 24
• Slide 25
• Slide 26
• Slide 27
• Slide 28
• Slide 29
• Slide 30
• Slide 31
• Slide 32
• Slide 33
• Slide 34
• Slide 35
• Slide 36