





Preview text:
BÀI 2: ỨNG DỤNG CỦA ĐỊNH LÍ THALÈS TRONG TAM GIÁC
THÂN MẾN CHÀO CÁC EM HỌC SINH
ĐẾN VỚI BÀI HỌC MỚI
CREDITS: This presentation template was created by
Slidesgo, and includes icons by Flaticon, and infographics & images by Freepik K H ỞI Đ Ộ N G
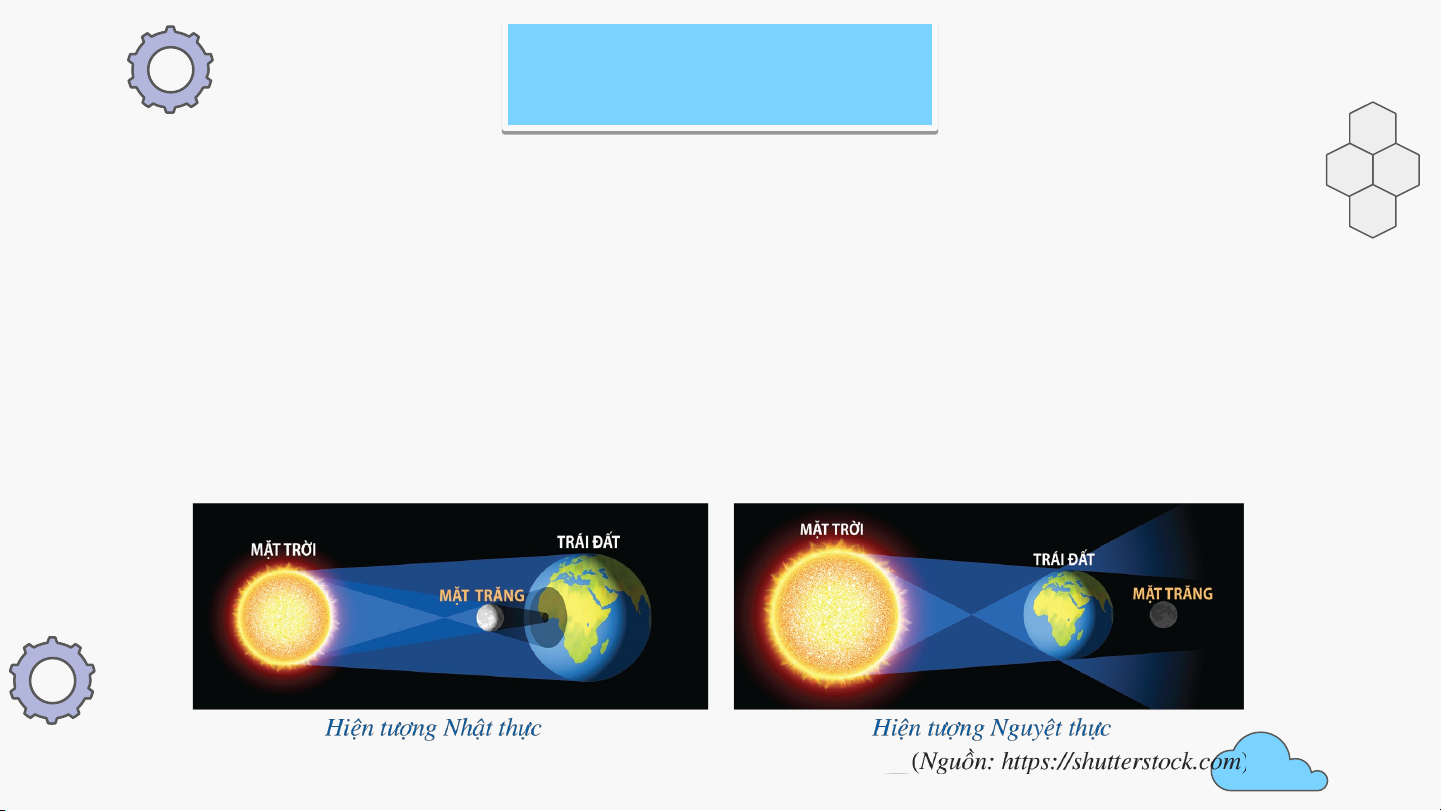
Từ xa xưa, con người đã muốn tìm hiểu về Mặt Trời, Trái Đất, Mặt Trăng,
chẳng hạn: Đường kính của mỗi hành tinh đó là bao nhiêu? Khoảng cách
từ Trái Đất đến Mặt Trăng và Mặt Trời là bao nhiêu? Dựa vào hiện tượng
Nhật thực và Nguyệt thực, các nhà toán học và thiên văn học Hy Lạp cổ
đại đã đưa ra câu trả lời cho những vấn đề trên. K H ỞI Đ Ộ N G Vào à th t ời đ iểm m xảy xả ra a Nh N ậ h t th t ực ự (N ( g N uyệ u t t thực) ự , c) đườ ư ng n kí k nh củ a a Mặ M t T r T ời và Mặ M t Tr T ă r ng g có có tỉ lệ ệ kho kh ảng n cá c ch t ừ ừ T r T á r i Đấ Đ t ấ đế đ n n Mặt ặ T r T ờ r i và và đến ế Mặ M t tT r T ă r ng g hay a khô kh ng n ?
BÀI 2: ỨNG DỤNG CỦA ĐỊNH LÍ THALÈS TRONG TAM GIÁC NỘI DUNG BÀI HỌC I Ước lượng khoảng cách II Ước lượng chiều cao I.
ƯỚC LƯỢNG KHOẢNG CÁCH
Thảo luận nhóm đôi, hoàn thành Ví dụ 1. Ví dụ 1
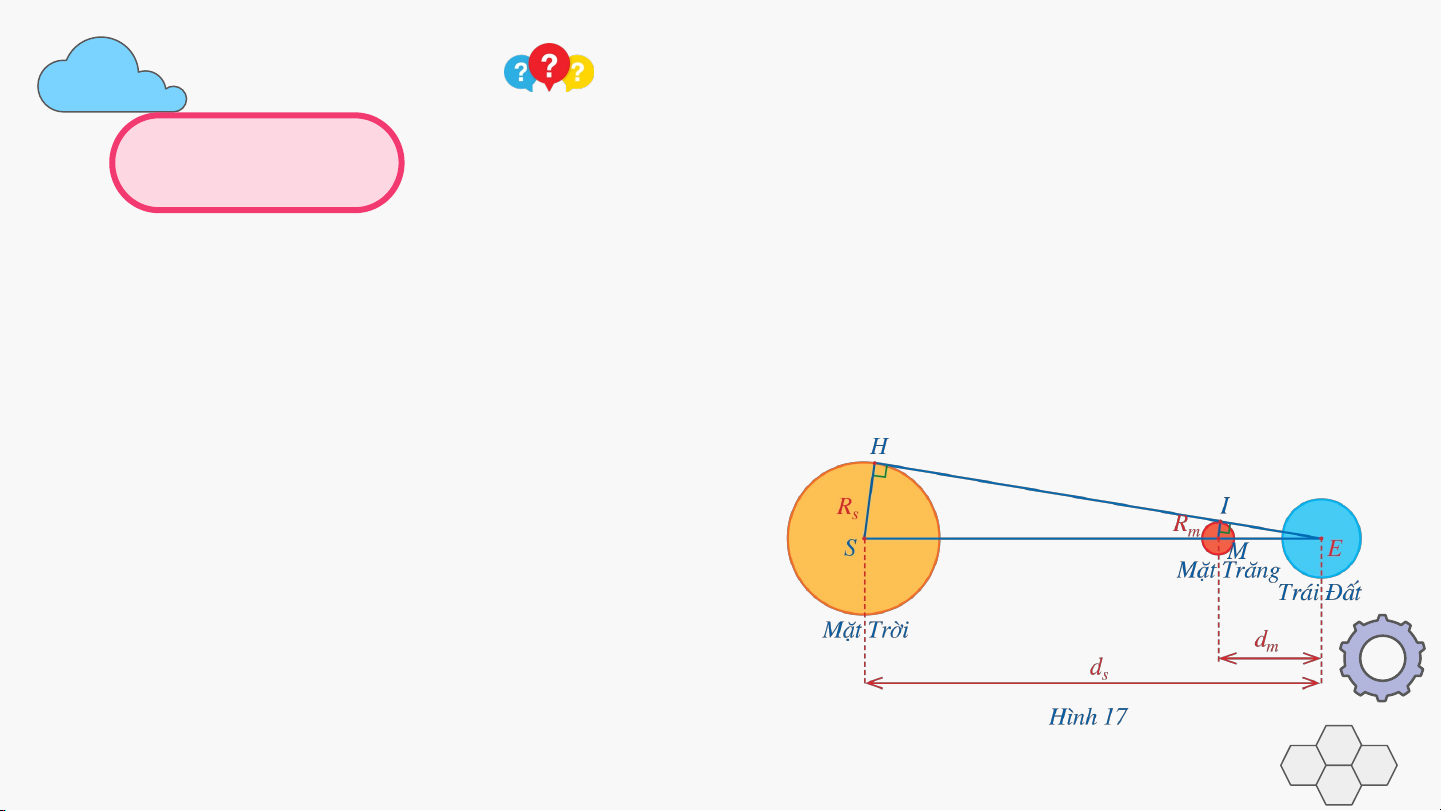
Hình 17 mô tả vị trí tương đối của Mặt Trời, Mặt Trăng và Trái Đất khi
xảy ra hiện tượng Nhật thực. Gọi khoảng cách từ Trái Đất đến Mặt Trời,
Mặt Trăng lần lượt là , .
Gọi bán kính của Mặt Trời, Mặt Trăng
lần lượt là , . Chứng minh Giải
Xét tam giác , ta có nên // .
Do đó, áp dụng hệ quả của định lí Thalès, ta có: . Vậy
Các nhà toán học và thiên văn học Hy Lạp cổ đại đã sử dụng
hệ thức trên và một số hệ thức có được từ hiện tượng Nguyệt
thực để ước lượng bán kính của Mặt Trời, Trái Đất, Mặt Trăng
cũng như khoảng cách từ Trái Đất đến Mặt Trăng và Mặt Trời. Ví dụ 2
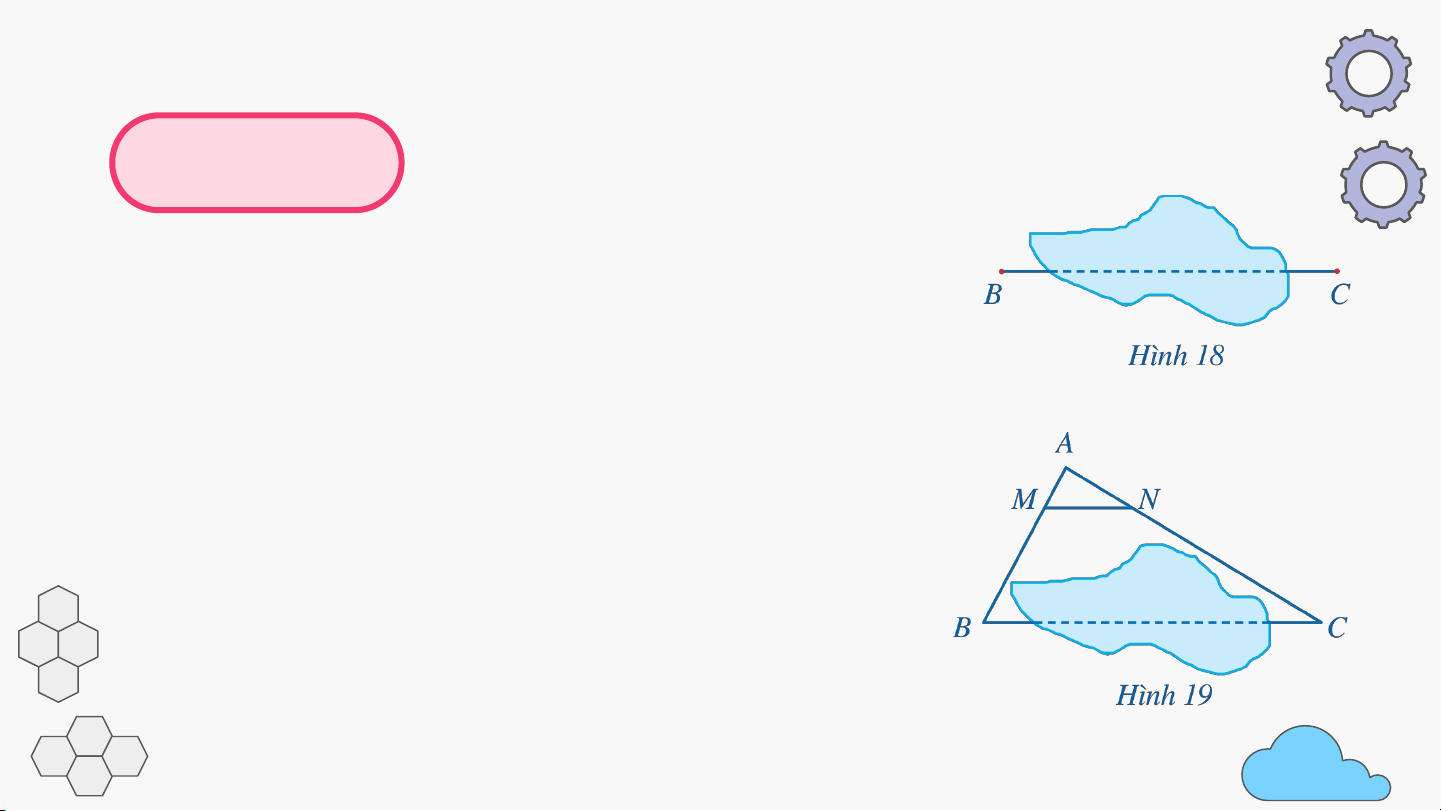
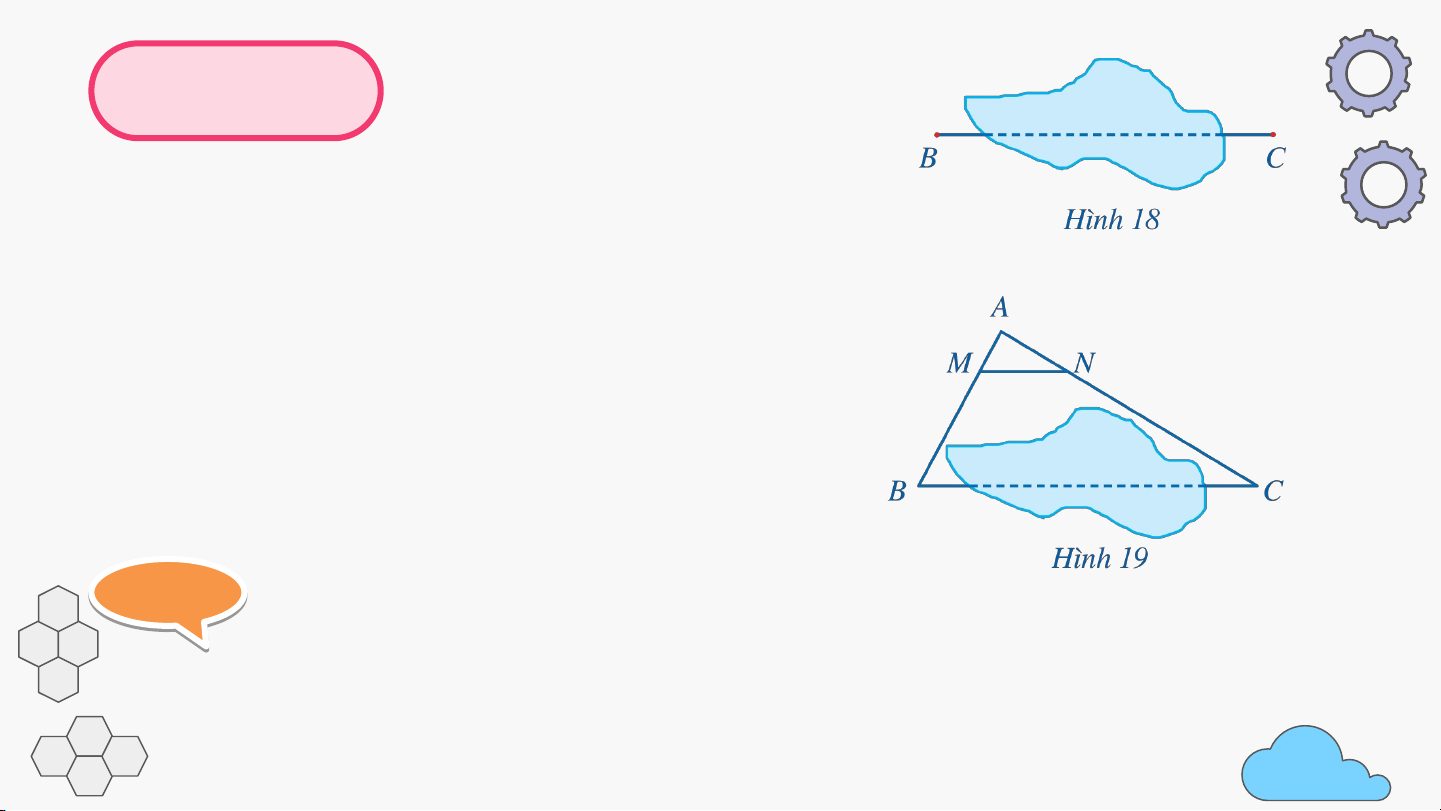
Để đo khoảng cách giữa hai vị trí và
như ở Hình 18 mà không thể đo trực tiếp, người ta
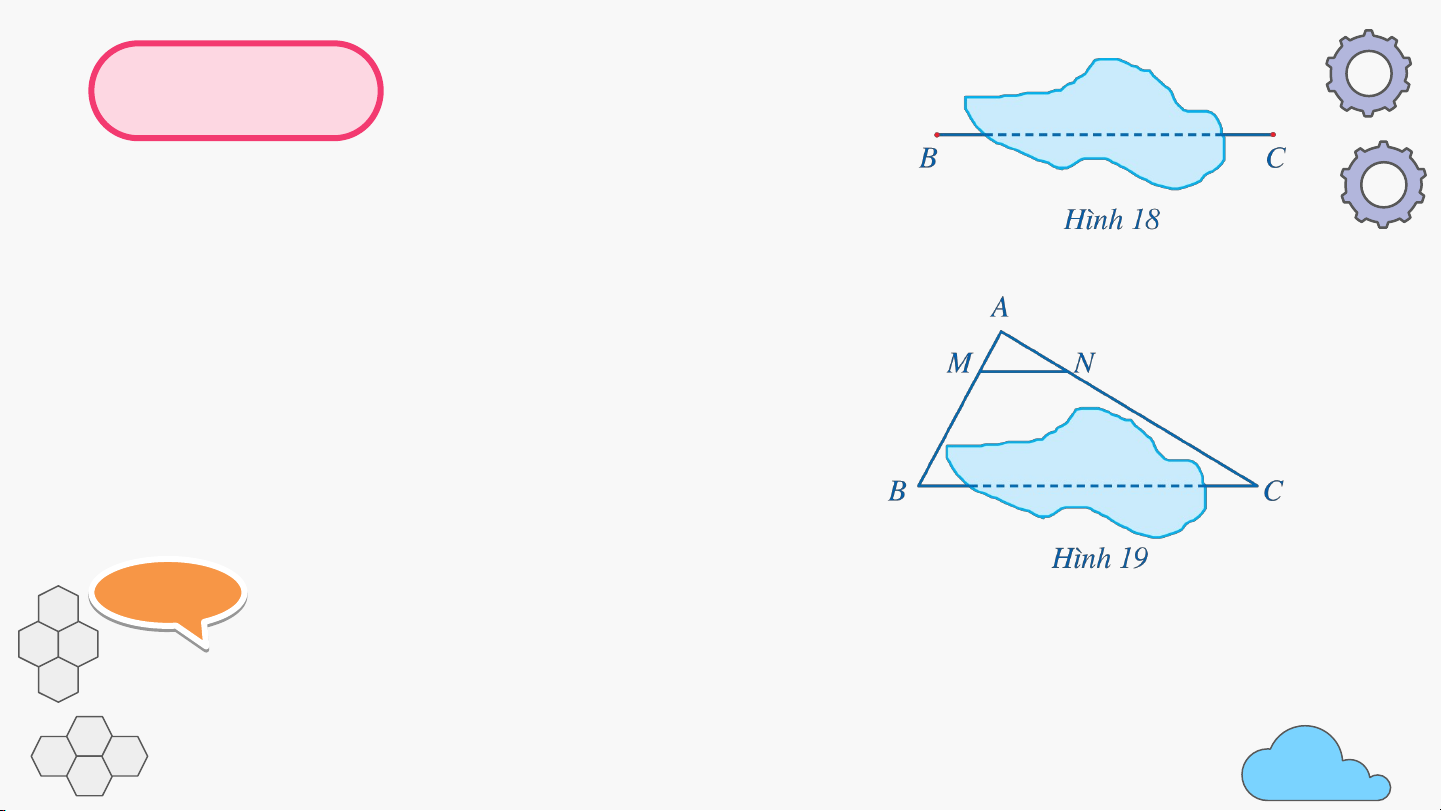
có thể làm như sau (Hình 19):
- Chọn điểm ở vị trí thích hợp và đo khoảng cách ,
- Xác định các điểm , lần lượt thuộc sao cho . Đo
độ dài các đoạn thẳng , Ví dụ 2
Từ đó tính được độ dài
a) Theo cách làm trên, nêu công thức tính
khoảng cách giữa hai vị trí và
b) Tính khoảng cách giữa hai vị trí và khi và Giải
a) Xét tam giác , ta có nên // (định lí Thalès đảo)
Suy ra (hệ quả của định lí Thalès). Do đó Ví dụ 2
Từ đó tính được độ dài
a) Theo cách làm trên, nêu công thức tính
khoảng cách giữa hai vị trí và
b) Tính khoảng cách giữa hai vị trí và khi và Giải b) Do nên . Suy ra
Vậy khoảng cách giữa hai vị trí và là Lu L yệ y n t n ậ t p 1 p Bạn Loan đặt một cái
que lên bàn cờ vua như ở Hình
20. Bạn ấy nói rằng: Không sử
dụng thước đo, có thể chia cái
que đó thành ba phần bằng nhau.
Em hãy giải thích tại sao.
Document Outline
- Slide 1
- THÂN MẾN CHÀO CÁC EM HỌC SINH ĐẾN VỚI BÀI HỌC MỚI
- Slide 3
- Slide 4
- Slide 5
- I
- I.
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13





