


















Preview text:
Biểu thức biểu thị tích của hình tạo bởi một tam giác
vuông và hai hình vuông dựng trên hai cạnh góc vuông
của nó (Hình 1.1) là : x y
Đó là một ví dụ về đa thức (hai biến) Hình 1.1
1 . KHÁI NIỆM ĐA TH TH ỨC
a) Đa thức và các hạng tử của đa thức.
Đa thức một biến là tổng của những đơn thức của cùng
một biến; mỗi đơn thức trong tổng đó gọi là một hạng tử của đa thức đó.
Một ví dụ về đa thức một biến : 2x3 – x2 + 1
1 . KHÁI NIỆM ĐA TH TH ỨC
a) Đa thức và các hạng tử của đa thức.
Học sinh viết ra hai đơn thức theo yêu cầu bài toán rồi trao đổi với bạn bên cạnh.
Sau đó cùng bạn sửa lại (nếu đơn thức đó viết chưa đúng).
1 . KHÁI NIỆM ĐA TH TH ỨC
a) Đa thức và các hạng tử của đa thức.
Chẳng hạn, bốn đơn thức được viết là 2 1 2 4x y ; ; x ; 2x y 2
Khi đó tổng bốn đơn thức là : 2 1 2 x y x x y 2 2 x y x 1 4 2 4 2 y x 2 2 2 1 6
x y x 2
1 . KHÁI NIỆM ĐA TH TH ỨC
a) Đa thức và các hạng tử của đa thức.
1 . KHÁI NIỆM ĐA TH TH ỨC
a) Đa thức và các hạng tử của đa thức.
Ta có thể viết A dưới dạng tổng của 6 đơn thức :
Vậy đa thức A có 6 hạng tử là :
1 . KHÁI NIỆM ĐA TH TH ỨC
a) Đa thức và các hạng tử của đa thức.
Các biểu thức là đa thức gồm : 2 3xy 1; 2x 3x
• Đa thức 3xy2 – 1 có hai hạng tử 3xy2 và – 1.
• Đa thức có hai hạng tử và .
1 . KHÁI NIỆM ĐA TH TH ỨC
a) Đa thức và các hạng tử của đa thức.
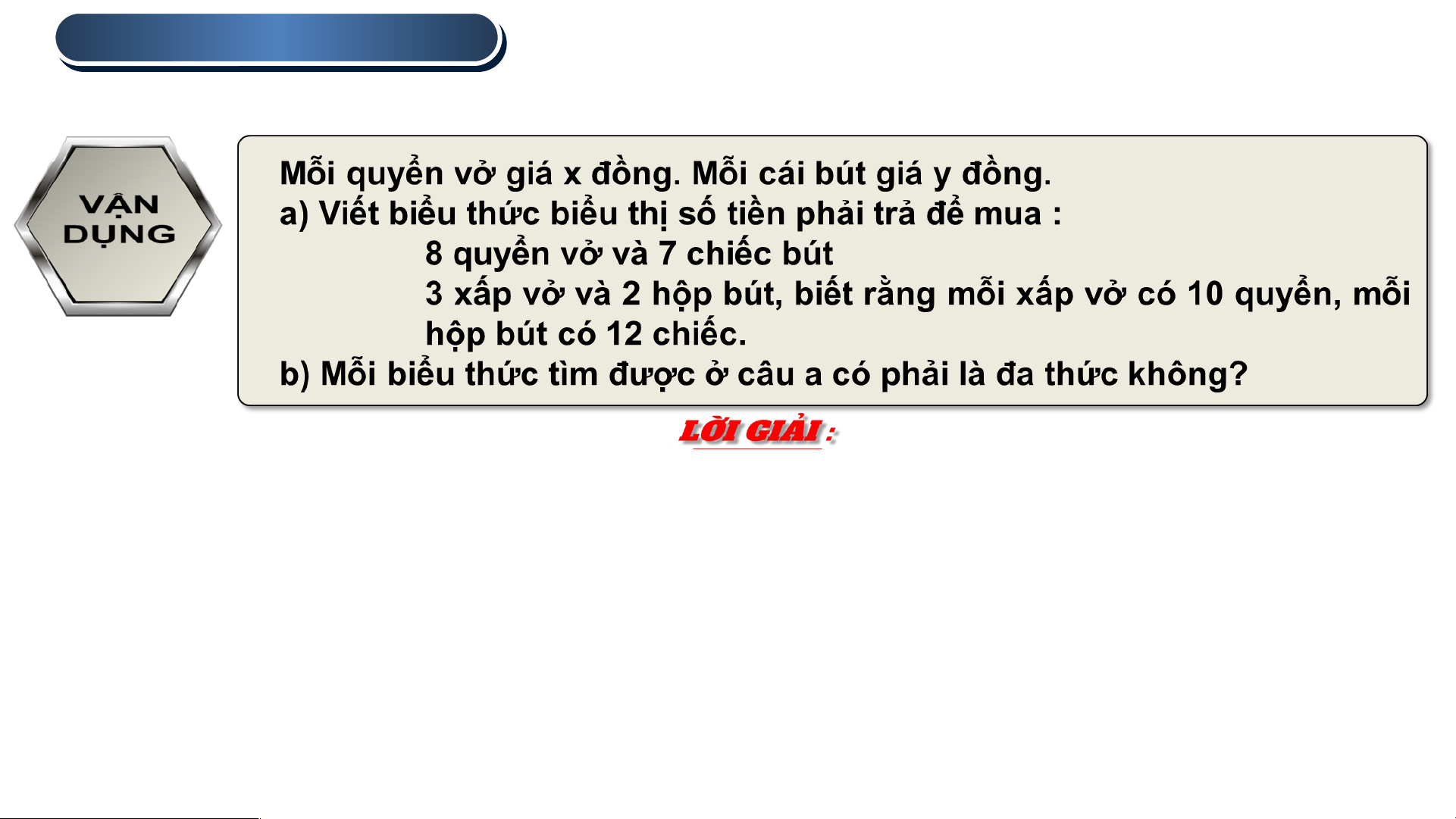
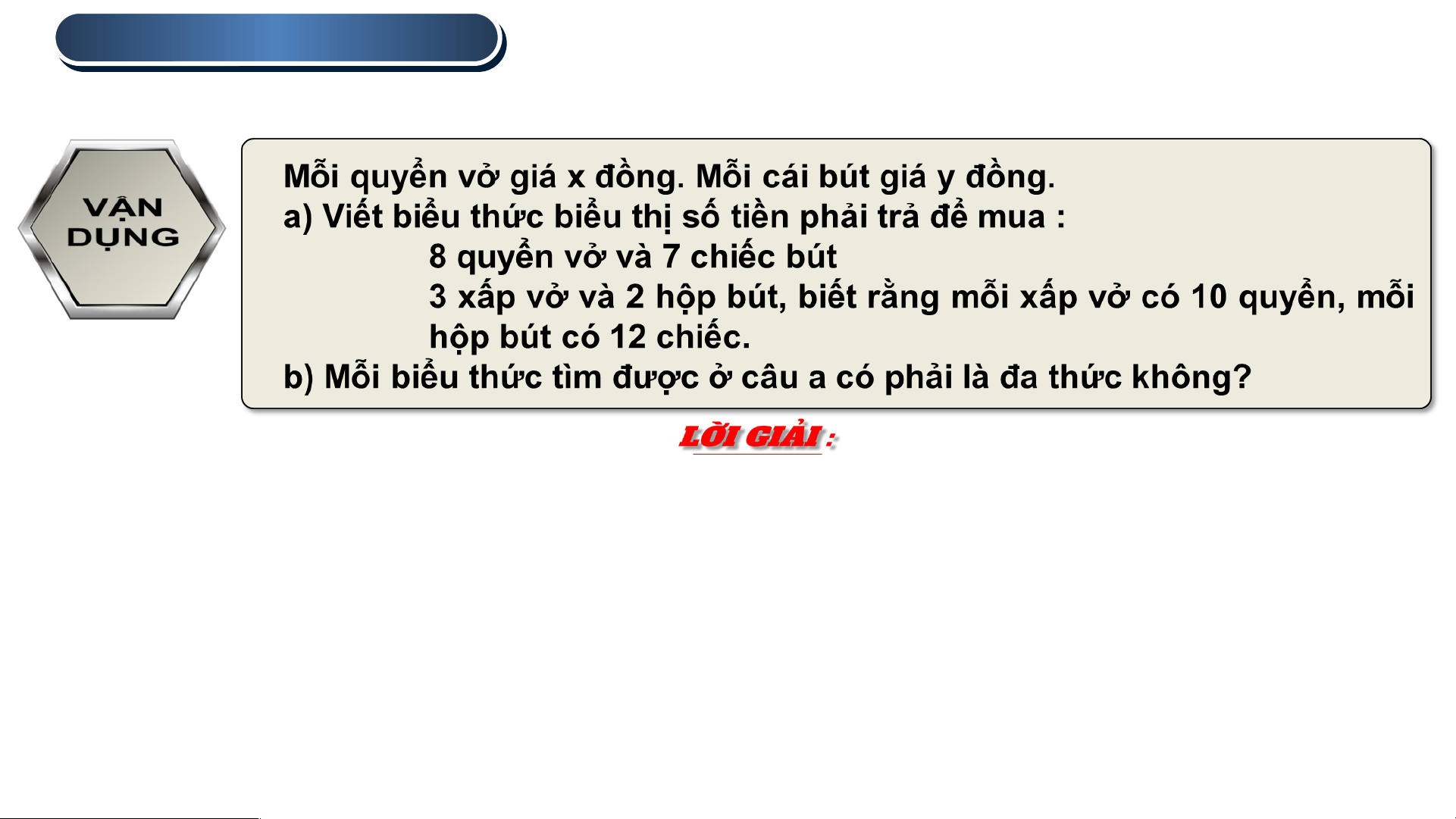
a) Giá tiền 8 quyển vở là: 8x (đồng), giá tiền 7 chiếc bút là: 7y (đồng)
Giá tiền 8 quyển vở và 7 chiếc bút là: 8x + 7y (đồng).
Mỗi xấp vở có 10 quyển nên 3 xấp vở có: 3 . 10 = 30 (quyển vở)
Giá tiền của 3 xấp vở là: 30x (đồng);
Mỗi hộp bút có 12 chiếc nên 2 hộp bút có: 12 . 2 = 24 (chiếc bút)
Giá tiền của 2 hộp bút là: 24y (đồng)
Giá tiền mua 3 xấp vở và 2 hộp bút là: 30x + 24y (đồng).
1 . KHÁI NIỆM ĐA TH TH ỨC
a) Đa thức và các hạng tử của đa thức.
b) Hai đa thức tìm được ở câu a lần lượt là: 8x + 7y; 30x + 24y
đều là các đa thức. 2 . ĐA THỨC TH TH U GỌN
b) Đa thức thu gọn, thu gọn một đa thức.
1. Xét đa thức : , có 2 hạng tử và là những đơn thức đồng dạng . Tương
tự hai hạng tử và cũng đồng dạng với nhau,
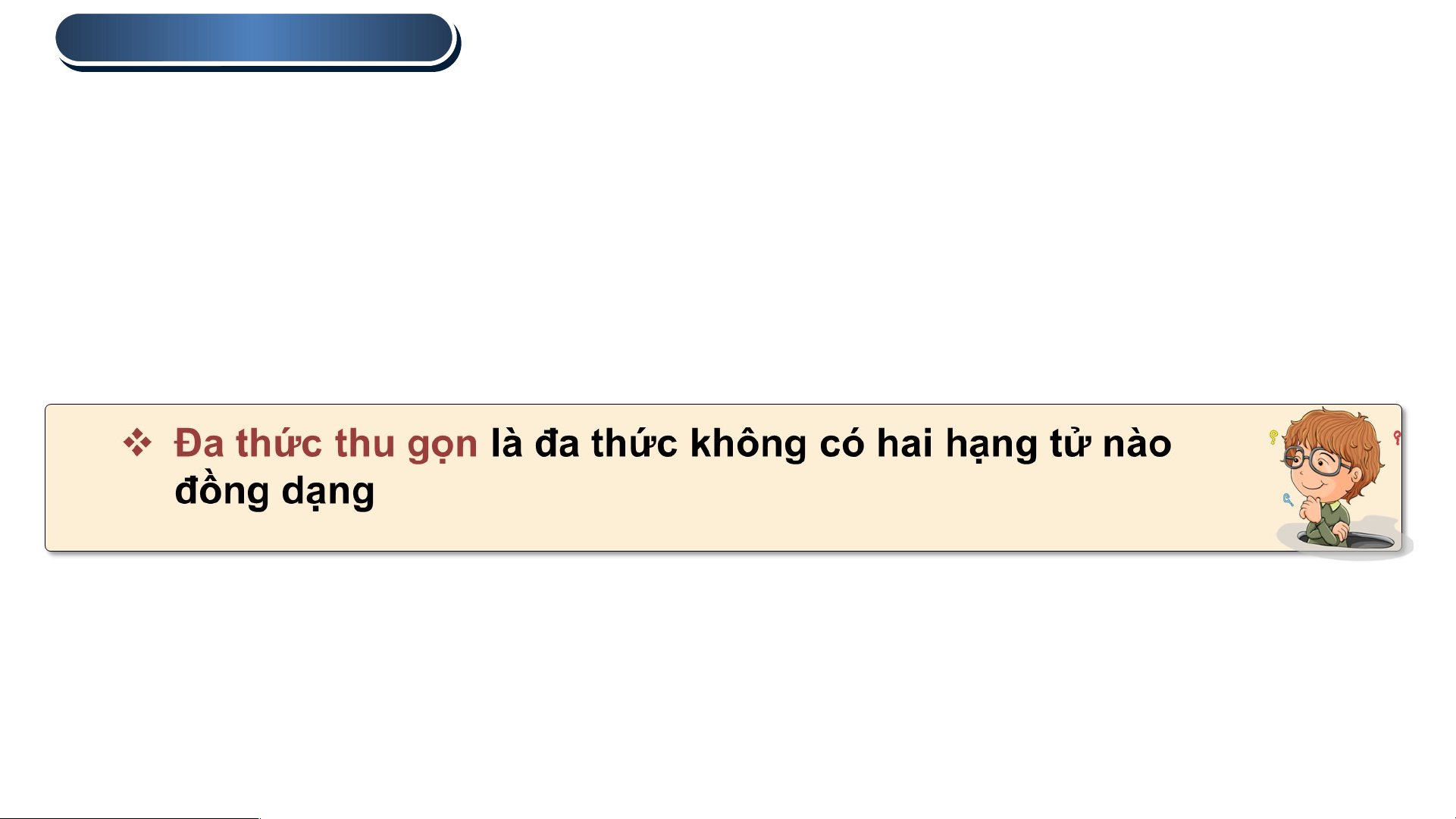
Trái lại , trong đa thức không có hai hạng tử nào đồng dạng. Ta nói A là
một đa thức thu gọn. 2 . ĐA THỨC TH TH U GỌN
b) Đa thức thu gọn, thu gọn một đa thức.
2. Với các đa thức có những hạng tử đồng dạng, ta có thể thu gọn chúng
Chẳng hạn, ta thu gọn đa thức B như sau : 2 2 2 B 2
x 3xy x 3y 5xy 2 2 2
2x x 3xy 5xy 3y
(Đổi chỗ và nhóm các hạng tử đồng dạng) 2 2 3
x 2xy 3y
(Cộng các hạng tử đồng dạng trong mỗi nhóm)
Đa thức 3 nhận được gọi là dạng thu gọn của đa thức B
CÂU HỎI : Đa thức nêu trong tình huống mở đầu có phải là đa thức thu gọn không? 2 . ĐA THỨC TH TH U GỌN
b) Đa thức thu gọn, thu gọn một đa thức. Ta có : M 2 2 x y x y 2 2 2 3
7xy xy 4xy 5xy2 2 2 4
x y 4xy 5xy 2 2 . ĐA THỨC TH TH U GỌN
b) Đa thức thu gọn, thu gọn một đa thức.
a) Thu gọn đa thức N, ta được: 2 2 2 1 4 2 2 2 4 2 N 5
y z 2xy z
x 2y z x xy z 3 3 2 2 2 2 5y z 2y z 2 2
2xy z xy 1 4 2 4 z x x 3 3 2 2 2 4 3
y z xy z x 2 . ĐA THỨC TH TH U GỌN
b) Đa thức thu gọn, thu gọn một đa thức.
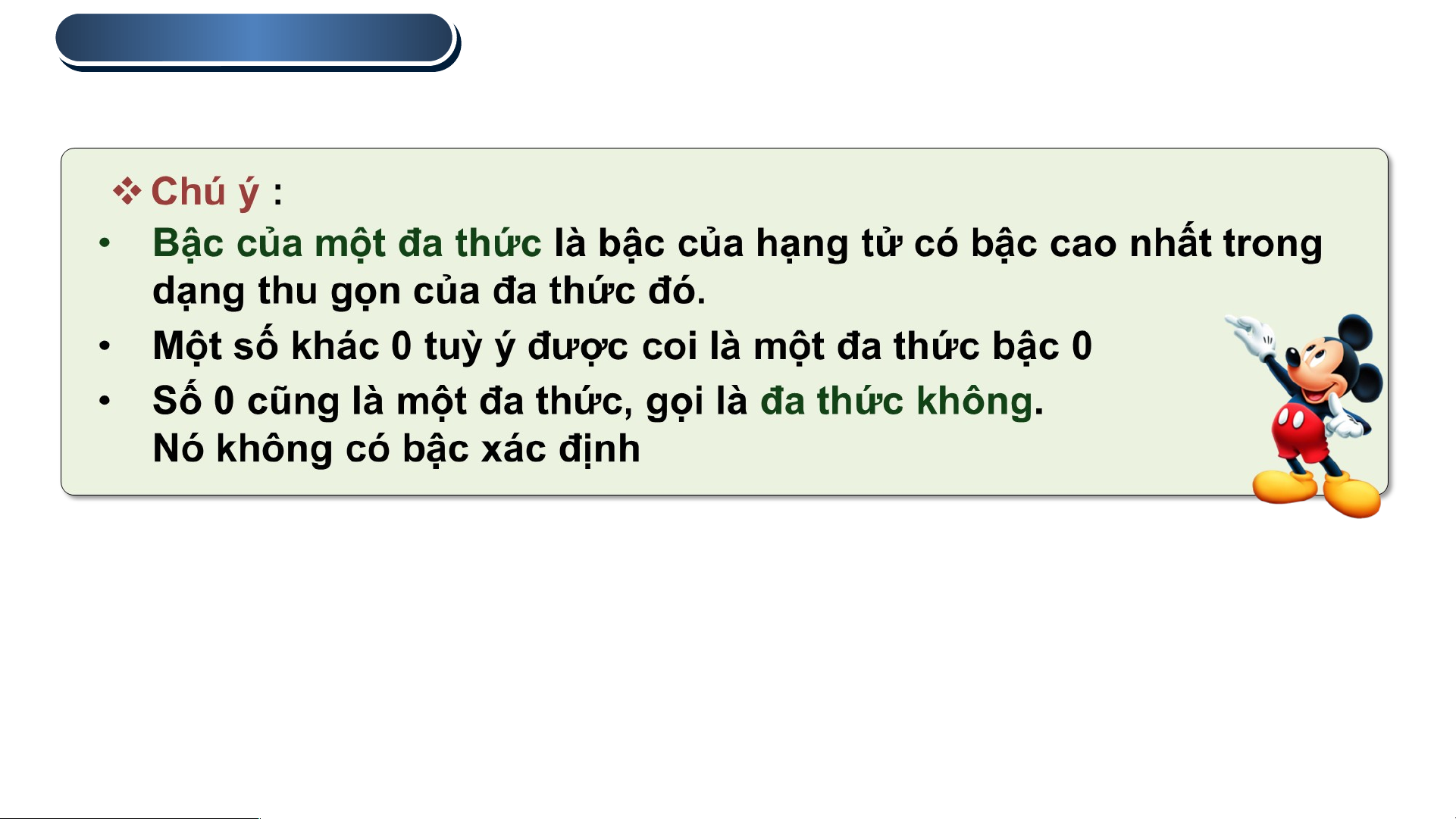
b) Dạng thu gọn của đa thức N có ba hạng tử gồm:
• Hạng tử 3y2z2 có hệ số là 3 và bậc là 4;
• Hạng tử −xy2z có hệ số là −1 và bậc là 4
• Hạng tử x4 có hệ số là 1 và bậc là 4. 2 . ĐA THỨC TH TH U GỌN
b) Đa thức thu gọn, thu gọn một đa thức. 2 . ĐA THỨC TH TH U GỌN
b) Đa thức thu gọn, thu gọn một đa thức.
a) Trước hết cần thu gọn P : P 4 4
3x 3x 1 4 2
xyz 2x y 6z 2
xyz 2x y 6z 3 3
Trong kết quả, 2 hạng tử và cùng có bậc 3, còn hạng tử có bậc 1. Vậy bậc của P là 3
b) Thay ; vào đa thức thu gọn của P, ta được : 2
P xyz 2x y 6z 1 6 2 3 2 . ĐA THỨC TH TH U GỌN
b) Đa thức thu gọn, thu gọn một đa thức.
a) Đa thức Q đã ở dạng thu gọn
• Đa thức Q có bậc là 2 1 3 b) Ta có : 5 3 2 2 5 2 H 4 x
x y x y 4x 2y 7 2 4 5 5
4x 4x 1 3 3 2 2 2
x y x y 2y 7 2 4 1 3 3 2 2 2
x y x y 2y 7
Đa thức H có bậc là 4. 2 4 2 . ĐA THỨC TH TH U GỌN
b) Đa thức thu gọn, thu gọn một đa thức.
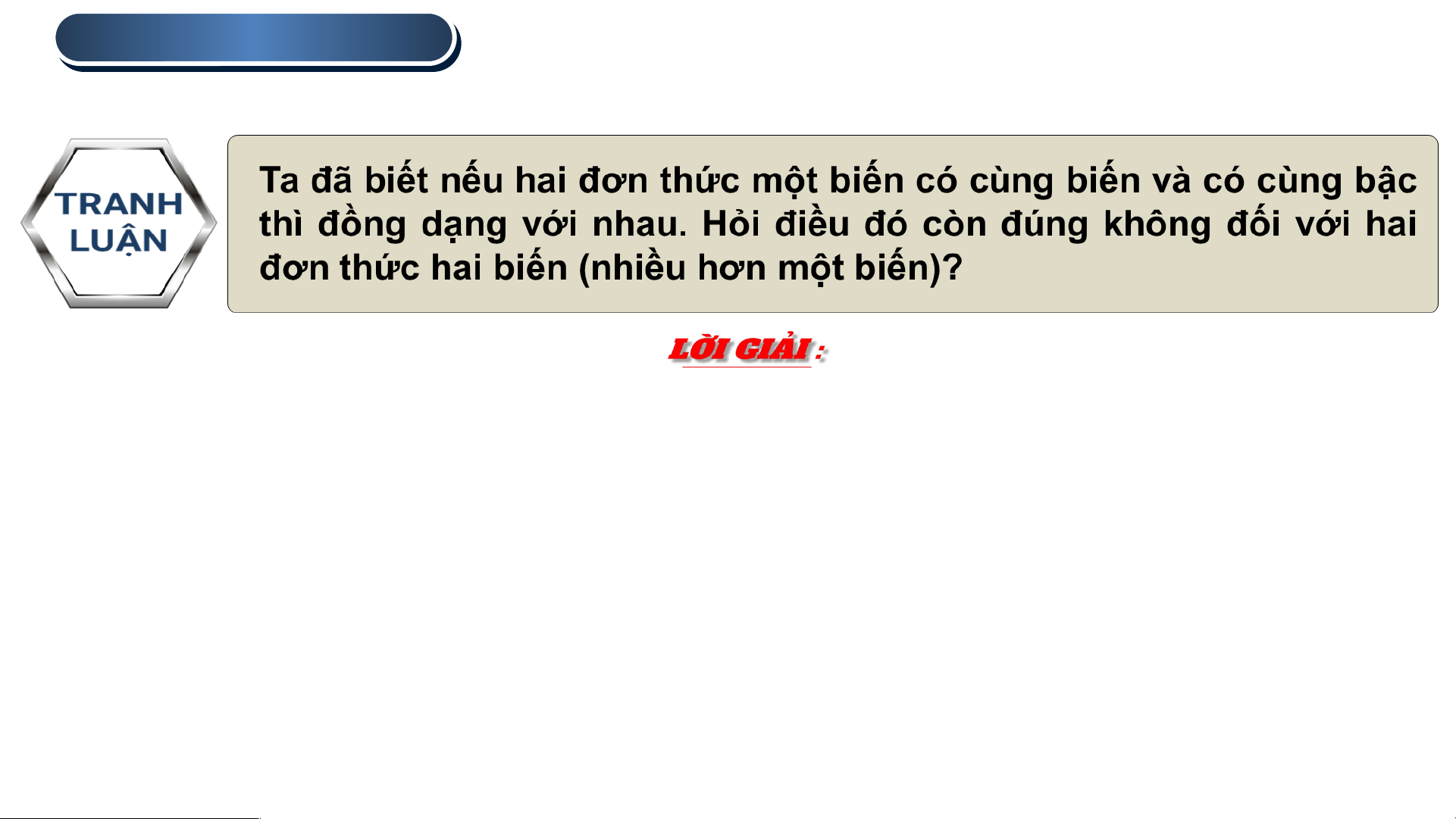
Hai đơn thức một biến có cùng biến và có cùng bậc thì đồng dạng
với nhau. Điều này không đúng với hai đơn thức hai biến (nhiều hơn một biến).
Chẳng hạn : Trong Hoạt động 4, cả ba đơn thức A, B và C đều có
cùng biến x, y và có cùng bậc nhưng chỉ có đơn thức A và B là
đồng dạng do có cùng phần biến x2y3.
Đơn thức C có phần biến x3y2 khác x2y3 nên không đồng dạng với hai đơn thức A, B.
• Các biểu thức là đa thức gồm : 2 2 2 x
x 3x1 ; 3x y 5 3 x y 2,4 ; ; 2024 5
• Các biểu thức không phải là đa thức gồm : x 5 1 ; x ; 2 5 x x x1 a) Xét đa thức : 2 2 2
x y 6xy 5x y 0,5x 4
• Hạng tử x2y có hệ số là 1, bậc là 3;
• Hạng tử –3xy có hệ số là –3, bậc là 2
• Hạng tử 5x2y2 có hệ số là 5, bậc là 4
• Hạng tử 0,5x có hệ số là 0,5, bậc là 1
• Hạng tử –4 có hệ số là –4, bậc là 0. b) Xét đa thức : 3 3 3
x 2 2xy y 7x y
• Hạng tử có hệ số là , bậc là 1
• Hạng tử −2xy3 có hệ số là −2, bậc là 4
• Hạng tử y3 có hệ số là 1, bậc là 3
• Hạng tử −7x3y có hệ số là −7, bậc là 4 4 3 3 3 2 2 3 4 )
a 5x 2x y 20xy 6x y 3x y xy y 4 x 3 3 x y x y 3 3 xy xy 2 2 4 5 6 2 20 3x y y 4 3 3 2 2 4 5
x 4x y 21xy 3x y y 3 2 2 3 2 )
b 0,6x x z 2,7xy 0,4x 1,7xy 3 3 x x 2 x z 2 2 0,6 0,4
1,7xy 2,7xy 3 2 2
x x z xy 4 2 2 2 4
a x x y xy x 4 4 x x 2 2 2 ) 3 3 1
3x y 3xy 1 2 2 2
3x y 3xy 1
Đa thức thu gọn ở trên có bậc là 4 nên đa thức đã cho có bậc là 4. 2 2 2 2 b
x y xy x x y x 2 2 x y x
y xy 2 2 ) 5 8 2 5 5 5 8 x 2x 2 8 xy x
Đa thức 8xy – x2 có bậc là 2 nên đa đã cho có bậc là 2. 1 1 1 Ta có : 2 2 2 2
M x y xy xy xy 5xy x y 3 2 3 1 2 1 2 2 1 2 x y x y xy xy
xy 5x y 3 3 2 3 2 xy 6xy 2
Thay và vào đa thức M , ta được : 3 2 3 2 9
M xy 6xy .0,5.1 6.0,5.1 2 2 4 a) Ta có : 2 2 2 2 2 2 2 2 2 P 8
x y z 2xyz 5y z 5x y z x y 3x y z 2 2 2 2 2 2
x y z x y z x y 2 2 2 8 3 5
z x y 2xyz 5y z 2 2 2
x y 2xyz 5y z
b) Thay x = –4; y = 2 và z = 1 vào đa thức P, ta được: 2 2 2 2 2
P x y 2xyz 5y z (
4) .2 2.( 4).2.1 1 6.4 8.2 5.4 1 00
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27




